“公共弦”的那些事儿

☉黑龙江省大庆市大庆实验中学 陈永志

苏教版高中数学《必修2》在“平面解析几何”一章中主要介绍了直线与圆的相关知识，这两部分内容都是高考考查的重点和热点，解析几何的本质就是运用代数方法来研究几何问题，所以此处必少不了相关的几何作图与代数运算，而学生往往由于作图能力与计算能力比较薄弱，从而害怕求解解析几何的题目.本文主要针对几道有关两圆相交时涉及的公共弦问题加以剖析，与大家共勉.

一、求公共弦方程

题目1已知圆C1：x2+y2=1，圆C2：x2+y2-2x-2y+1=0，试求两圆的公共弦所在的直线的方程.

思路分析1：因为两圆的公共弦由两圆相交时产生的两个交点确定，所以最直接的解法就是先求出两圆的交点坐标，然后再去求公共弦所在的直线方程.

解法1：将两圆的方程联立得，解得即两圆的交点为（0，1），（1，0），所以公共弦所在直线的斜率为k=-1.故公共弦所在的直线方程为y=-x+1.

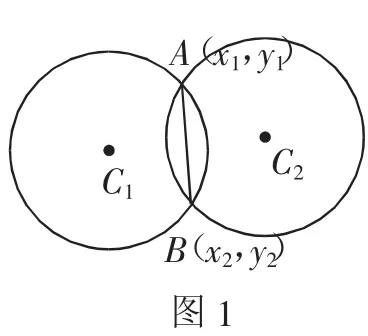
思路分析2：如图1所示，不妨设两个公共点的坐标分别 为 A（x1，y1），B（x2，y2），所 以于是①-②可得x1+y1-1=0，这就说明点A（x1，y1）在直线x+y-1=0上.同理可得点B（x2，y2）也在直线x+y-1=0上，这样由点A（x1，y1），B（x2，y2）确定的直线方程就是x+y-1=0，即两圆的公共弦所在的直线方程.

解法2：将两圆的方程联立得，将两个方程相减，整理得x+y-1=0，所以圆C1与圆C2的公共弦所在的直线方程为x+y-1=0.

点评：很明显，在解法1中，由于需要解二元二次方程组，其计算量不言而喻，这也是大部分学生不希望遇到的，而解法2避开了解方程组，大大弱化了计算量，也为我们提供了一种便捷的求公共弦所在直线方程的途径，即两圆方程相减，消去二次项，便可得到公共弦所在的直线方程.

二、求公共弦长

题目2求圆C1：x2+y2=9与圆C2：x2+y2-4x+2y-3=0的公共弦长.

思路分析1：只要求出圆C1和圆C2的两个公共点的坐标，然后利用平面上两点之间的距离公式即可求得公共弦长.

思路分析2：我们常用的求弦长的方法是：作出圆心到弦的距离，连接圆心与两圆的交点，从而构造出直角三角形，进而利用勾股定理解题.

解法2：如图2所示，作出圆C1和圆C2的简图，将圆C1与圆C2的方程相减，得到公共弦AB所在的直线方程2x-y-3=0，又圆心C（10，0），则圆心C1到公共弦AB的距离，而圆C的半径r=3，所以|AB|=11

图2

图3

解法3：我们知道，两圆相交时，两圆圆心的连线垂直平分公共弦，于是连接C1C2，交AB于点H，连接C1A、C2A，如图3所示，根据圆心C（10，0），C（22，-1），易求得圆心距|C1C2|=，而|C1A|=3，|C2A|=2，可设|C1H|=x，则|C2H|=x，利用勾股定理有|C1A|2-|C1H|2=|C2A|2-|C2H|2，即9-x2=8-（-x）2，解得，所以|AH|=故公共弦长|AB|=2|AH|=

点评：解法2与解法3侧重于图形中的几何运算，也是直线与圆中解决弦长问题最常用的方法，点到直线的距离公式的记忆以及对圆中与弦有关的性质的熟练掌握是解题的关键.

三、与公共弦有关的综合问题

题目3已知圆C：x2+y2-2x+4y-4=0，是否存在斜率为1的直线l，使得以l被圆C截得的弦AB为直径的圆过原点？若存在，求出直线l的方程；若不存在，请说明理由.

思路分析：这是一道存在性的探究题，首先，解题时要注意答题格式的规范性，其次，如何理解并转化“使得以l被圆C截得的弦AB为直径的圆过原点”这句话？一种理解：将以AB为直径的圆的方程表示出来，并代入原点坐标来求解；另一种理解：因为AB为直径，所以∠AOB=90°，再将直角关系转化为两垂直直线的斜率之间的关系，或者转化成两垂直向量之间的数量积关系.

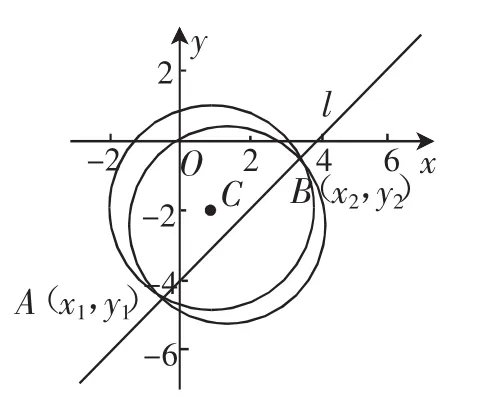
图4

解法1：假设存在斜率为1的直线l，使得以l被圆C截得的弦AB为直径的圆过原点，不妨设直线l的方程为y=x+m，与圆C的两个交点分别为A（x1，y1），B（x2，y2），以AB为直径的圆过原点，如图4所示，将直线l的方程y=x+m代入圆C的方程中，整理得2x2+（2m+2）x+m2+4m-4=0.因为直线l与圆C相交，所以Δ=（2m+2）2-8（m2+4m-4）>0，解得-3-3

解法2：前同解法1，因为以AB为直径的圆过原点，所以=0，即x1x2+y1y2=0.所以x1x2+（x1+m）（x2+m）=0，整理得2x1x2+m（x1+x2）+m2=0，于是m2+4m-4+m2-m（m+1）=0，解得m=1或m=-4，均符合题意.故存在斜率为1的直线l：y=x+1或y=x-4，使得以l被圆C截得的弦AB为直径的圆过原点.

解法3：假设存在斜率为1的直线l，使得以l被圆C截得的弦AB为直径的圆过原点，不妨设直线l的方程为xy+m=0，注意到弦AB不仅是直线l被圆C截得的弦，更是以AB为直径的圆与圆C的公共弦，这样一来，我们可以先写出过A、B两点的圆系方程：x2+y2-2x+4y-4+λ（x-y+m）=0，整理得x2+y2+（λ-2）x+（4-λ）y+mλ-4=0，则圆心的坐标为），因为圆过原点，故mλ-4=0 ①，又圆以AB为直径，所以圆心）满足直线方程xy+m=0，即+m=0 ②，结合①②两式，解得m=1或m=-4，均符合题意.故存在斜率为1的直线l：y=x+1或y=x-4，使得以l被圆C截得的弦AB为直径的圆过原点.

点评：在三种解法中，解法1直接紧扣题意，通过“死算”，求得以AB为直径的圆的方程后得解，解法2实施了非常有效的转化，但我们只是转化为垂直向量的数量积之间的关系，其实也可以转化成垂直的直线斜率之间的关系，这两种解法中，根与系数的关系的运用是关键，而解法3则运用了圆系方程来求解，其计算量小，且正确率高.

直线与圆这部分内容是解析几何中的重点与难点，解决此类问题都会有一定的计算量要求，并会运用数形结合的数学思想方法来解题，所以老师在平时的教学活动中，要指导学生细心审题，准确作图，认真计算，不忘检验，逐步培养学生严谨的数学思维，从而提高学生的数学解题能力.F