齐次化法在求解最值问题中的应用

☉甘肃省白银市第一中学 胡贵平

若不等式两边各项的次数相等，则我们称之为齐次不等式.许多条件不等式问题通过化成齐次不等式来解决，都能起到很好的解题效果.

例1（2017年山东卷12题）已知直线=1（a＞0，b＞0）过点（1，2），则2a+b的最小值为______.

即a=2，b=4时取得等号.

所以2a+b的最小值为8.故填答案：8.

这是一道条件求最值问题，解决本题的方法有很多，已知“和式”为常数1，所求也是“和式”，且两个“和式”都是齐次式，最常见的方法是“1的代换”法.“1的代换”法的优势在于避免了多次使用基本不等式时“=”不易取得的错误.

例2已知x，y均为正实数，满足x+2y=1，则的最小值为______.

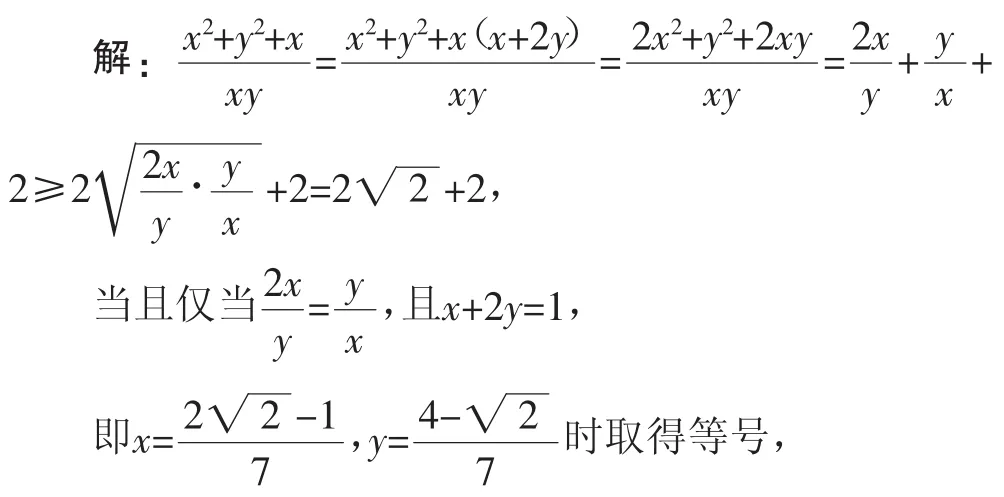
“1的代换”的实质是构造齐次式，分母是二次式，分子中x2、y2是二次式，而x是一次式，通过“1的代换”构造分子是二次式，再应用基本不等式求最值.

例3（2018年全国高中数学联赛甘肃预赛4题）若正实数x，y满足y＞2x，则的最小值是______.

解：x，y是正实数，y＞2x，所以

该问题为齐次式，巧妙地转化为利用基本不等式求解的结构，利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧以及“一定、二正、三相等”的约束条件.

例4 已知实数x，y满足x2+y2-xy=2，则x2+y2+xy的取值范围是______.

所以x2+y2+xy∈].故填答案，6].

以不等式或函数为背景（本题用到对勾函数）的最值问题，充分地利用了题中的条件以及结构，构造出合适的齐次式，最终达到消元的目的，进而解决问题.

例5已知正实数x，y满足xy≤1，则的最小值为______.

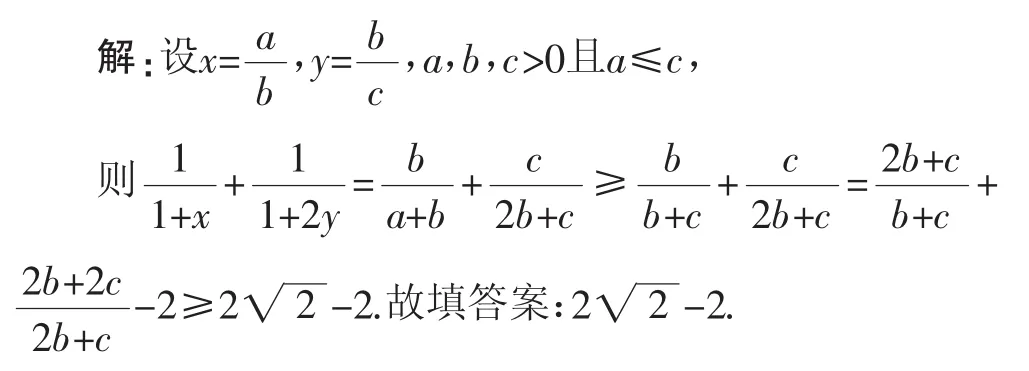
把条件进行合适的变形，转化为齐次不等式，为了凑基本不等式的积为定值，换元后进行了一次放缩，齐次换元形式应依照条件的样式进行调整.

例6（2013年全国新课标Ⅱ文、理24题）设a、b、c均为正数，且a+b+c=1，证明：

证明：（1）所证不等式的左边是二次式，右边是零次式，由已知a+b+c=1，所以（a+b+c）2=1，从而要证的不等式可化为齐二次不等式ab+bc+ac（a+b+c）2，即证ab+bc+ac≤a2+b2+c2.

而a2+b2+c2-（ab+bc+ac）=a-b）2+（b-c）2+（c-a）2］≥0.所以原不等式成立.

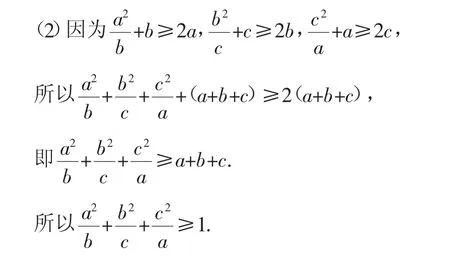
许多重要不等式如基本不等式、柯西不等式自身就是齐次不等式，所以证明一些带条件的非齐次不等式时，利用所给条件对原不等式的结论进行恒等变形，转化为齐次不等式，最终化为易于证明的形式.W