从一道课本习题看“阿波罗尼斯”圆

☉甘肃省兰州市第十中学 温庆峰

题目已知点M与两个定点O（0，0），A（3，0）的距离之比为，求点M的轨迹方程.

解析：如图1所示，设动点M（x，y），连结MO，MA，有：|MA|=

化简得：x2+y2+2x-3=0，

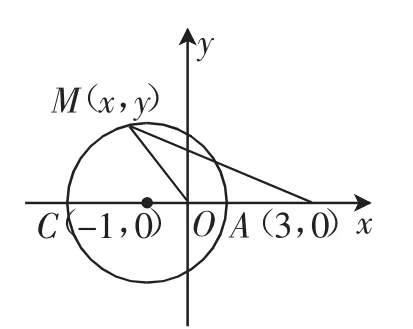
图1

则方程（1）即为所求点M的轨迹方程，它表示以C（-1，0）为圆心，2为半径的圆.

这是人教A版高中数学必修2（P124 B组，3题）的一道习题，若对教材进行二次开发，从系统的高度切入，可以进行从特殊到一般的推广探究，还可以分析挖掘出这道题的几何背景，题中所求出的圆，我们习惯上称这种圆为“阿波罗尼斯”圆.“阿波罗尼斯”圆不仅是具有数学文化的探究素材，而且在高考中以它为背景的考题也经常出现.

背景展示：阿波罗尼斯（Apolloning，约公元前260～170），是古希腊著名的数学家，与欧几里得、阿基米德一起被称为亚历山大时期的数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要的研究成果集中在他的代表作《圆锥曲线》一书中，阿波罗尼斯圆是他的研究成果之一.

将上面的习题推广到一般形式，这就是人教A版高中数学必修2（P144 B组，2题）的一道复习参考题.

推广：已知点M（x，y）与两个定点M1，M2距离的比是一个正数m，求点M的轨迹方程，并说明轨迹是什么图形（考虑m=1和m≠1两种情形）.

解析：以线段M1M2所在的直线为x轴，线段M1M2的垂直平分线为y轴，建立平面直角坐标系，设M1（-a，0），M2（a，0）（a＞0）.

化 简得：（1-m2）x2+（1-m2）y2+2a（1+m2）x+（1-m2）a2=0，（1）

①当m=1时，方程为x=0，图形是直线x=0，也就是线段M1M2的垂直平分线（定义这样的直线为阿波罗直线）；

几何画板探究：如图2所示，即得轨迹问题

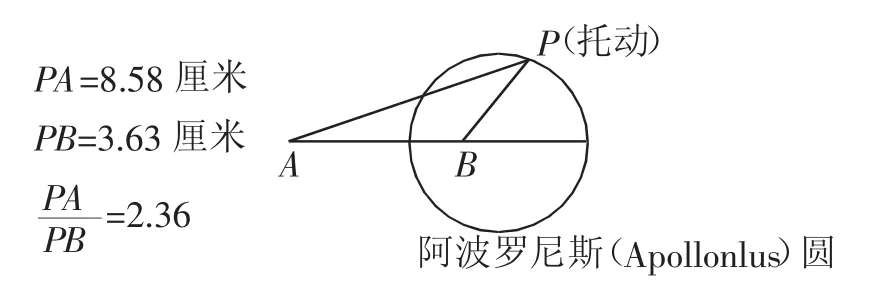
图2

通过几何画板进行简单的几何实验，构造出了符合条件的图形，激发了学生观察思考、动手实践、交流探究的能力.

人教A版高中数学必修2（P139）信息技术应用，用几何画板探究点的轨迹.

例1已知点P（2，0），Q（8，0），点M与点P的距离是它与点Q的距离的，用《几何画板》探究点M的轨迹，并给出轨迹的方程.

通过探究知道：到两个定点的距离之商为定值的点的轨迹是圆，然后就可以引发学生探究：

（1）到两个定点的距离之和为定值的点的轨迹是椭圆.

（2）到两个定点的距离之差的绝对值为定值的点的轨迹是双曲线.

（3）到两个定点的距离之积为定值的点的轨迹是卡西尼卵形线.

掌握了探究方法，椭圆、双曲线的学习就会变得轻而易举了，这样以题练技，以技通法，明在阅读题目后将其翻译成数量关系，暗在学思维、找工具、找方法，培养数学思维、数据处理能力.

例2（2013·江苏卷17题）如图3所示，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆C的半径为1，圆心在l上.若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围.

解析：点C在直线l：y=2x-4上，故设C的坐标为（a，2a-4）.因为半径r1=1，所以圆C的方程是：（x-a）2+［y-（2a-4）］2=1.

设点M（x，y），则由|MA|=2|MO|可得点M的轨迹正是阿波罗尼斯圆D，即

化简整理得：x2+（y+1）2=4.

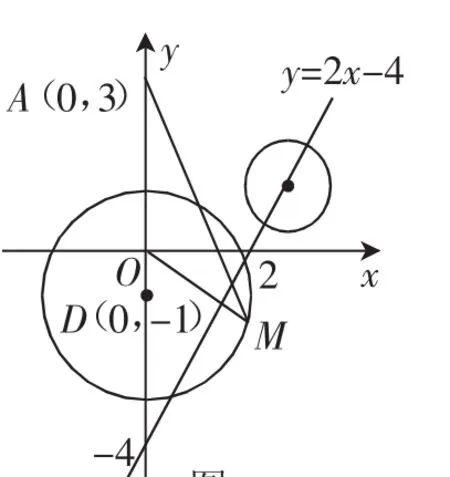
图3

所以点M（x，y）在以D（0，-1）为圆心，r2=2为半径的圆上.又点M（x，y）在圆C上，所以两圆有公共点的条件是：|r-r|≤|DC|≤|r+r|，即1≤5a2-12a+9≤9，解得0≤1212

评注：由图3可以直观地观察出两圆公共点的变化情况，当a=0时，圆C为x2+（y+4）2=1与所求圆D相切；当a=时，圆C为=1，也与所求圆D相切.这样，答案0≤a的正确性也就不言而喻了.

例3（2014·湖北卷文17）已知圆O：x2+y2=1和点A（-2，0），若定点B（b，0）（b≠-2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则：

（1）b=______；（2）λ=______.

评注：解本题的常用方法是“坐标转移法”，但是条件中依然有比例，所以仍然可以采用“阿波罗尼斯圆”来处理.

例4（2008·江苏卷，13题）满足条件AB=2，AC=的△ABC的面积的最大值是______.

图4

解析：建立如图4所示的平面直角坐标系，因为c=1，λ=，代入阿波罗尼斯圆公式得：（x-3）2+y2=8.设圆心为M，显然当CM⊥x轴时，△ABC面积最大，此时|CM|=，所以（故填答案

评注：显然这又是一例“阿波罗尼斯圆”，既然△ABC存在，说明其轨迹不包括与x轴的两个交点P，Q，由于所以CP为△ACB的内角平分线；同理，CQ为△ACB的外角平分线.这就是说，P，Q分别是线段AB的内分点和外分点，而PQ正是阿氏圆的直径.于是“阿波罗尼斯圆”又被称为“内外圆”.因此，上例又有如下的解法：

解析二：因为动点C到定点A（-1，0）和B（1，0）的距离之比为，则有|x+1|=|x-1|，整理得x2+2x+1=2（x2-2x+1），即x2-6x+1=0，解得x1=3-2，x2=3+2，所以x1=3-2为内分点，x2=3+2为外分点.圆半径（x-x）=2即为三角形高的最大值，即△ABC高的最大值是2故△ABC面积的最大值是2F