考题中常见的切线问题

广东

近期笔者在为学生解惑的过程中常遇到与切线有关的问题，有求函数图象的切线方程，也有求圆锥曲线的切线方程.在指导学生解答2018年全国卷Ⅲ文科第21题的过程中，除了遇到求函数图象的切线方程之外，还发现了利用曲线切线不等式的解题方法，此解法既为解决函数与导数的综合考题开辟了新的解题途径，也实现了复杂的解题过程简单化.由于切线问题以各种形式频繁出现于高考试题之中，所以深入钻研高考试题中常见的切线问题是十分必要的.

一.高考对切线问题的考查

为了掌握高考对切线问题的考查力度和考查形式，笔者对2016至2018年全国卷Ⅰ、卷Ⅱ、卷Ⅲ的文、理科试卷进行了统计汇总成下表.从表格可以看出，各地每年的高考试卷都重视对切线问题的考查，而且考查力度有不断加大的趋势，2018年更为明显.

近三年全国高考卷中考查切线问题的试题分布

二.函数图象的切线问题

1.求函数图象的切线方程

【例1】(2018·全国卷Ⅰ·文6理5)设函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数，则曲线y=f(x)在点(0,0)处的切线方程为

( )

A.y=-2xB.y=-x

C.y=2xD.y=x

解析：由于f(x)为奇函数，所以a-1=0，解得a=1，则f(x)=x3+x，f(0)=0.又由于f′(x)=3x2+1，则f′(0)=1，所以曲线y=f(x)在点(0,0)处的切线方程为y=x，则正确的选项为D.

【例2】(改编题)设函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数，则曲线y=f(x)过点(1,2)的切线方程为________.

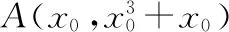
综上所述，曲线y=f(x)过点(1,2)的切线方程为4x-y-2=0或7x-4y+1=0.

【评注】例1既是2018年全国卷Ⅰ文科第6题，也是理科第5题.考查的是求函数f(x)图象上指定点(x0,f(x0))处的切线方程，解决方法也不难，就是先求函数f(x)在指定点处的导数f′(x0)，得到切线斜率，然后求切线方程y-f(x0)=f′(x0)(x-x0).若所考查的是过指定点(m,n)的函数图象的切线方程，则应该先设切点，再按上述方法求切线方程，然后将点(m,n)代入切线方程，从而求得切点坐标，进而得切线方程，如例2.

2.两函数图象的公切线问题

【例3】(2015·全国卷Ⅱ文·16)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切，则a=________.

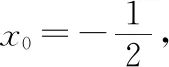
【评注】该题是2015年全国卷Ⅱ文科第16题，是两函数图象的公切线问题.由于可以直接求出函数y=x+lnx的图象在指定点(1,1)处的切线方程y=2x-1，所以该题可以转化为：已知切线方程y=2x-1，求函数y=ax2+(a+2)x+1解析式中的参数.考生可以先求函数的导函数，令导函数的值等于切线的斜率，便能确定切点的横坐标，再将横坐标代入曲线(或切线)方程就得到切点纵坐标，将切点坐标代入曲线(或切线)方程便可求得参数的值.如果函数为二次函数，那么也可以由联立方程组，消元得一元二次方程，然后由Δ=0去求解.

三.圆锥曲线的切线问题

1.求抛物线的切线方程

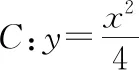
(Ⅰ)当k=0时，分别求C在点M和N处的切线方程；

(Ⅱ)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？请说明理由.

(Ⅱ)存在符合题意的点.证明略.

【评注】该题是2015年全国卷Ⅰ理科第20题，考查求抛物线x2=2py的切线方程，教材(新课标人教A版)介绍了两种解法，其中“判别式法”是通性通法，解答的过程为：如果切线的斜率存在，那么设切线的方程为y=kx+b，联立得方程组，消去x(或y)，由Δ=0得到斜率(或斜率的关系式)；如果切线的斜率不存在，那么由图形确定切线的方程.另外一种方法就是利用函数在某一点处导数的几何意义去求切线的斜率，笔者称其为“导数法”.由于利用“导数法”的运算量少，并且解答过程也不烦琐，所以备受师生青睐.但是教材只介绍了利用“导数法”去求抛物线x2=2py的切线方程，那么方程为y2=2py的抛物线和其他的圆锥曲线,它们求切线方程是否也可以使用“导数法”呢?

2.借助导数求圆锥曲线的切线方程

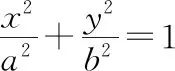
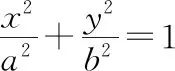
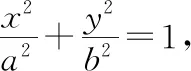
同理可证得以下双曲线和抛物线的切线方程.

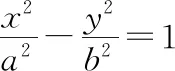
公式三：若点P(x0,y0)在抛物线y2=2px上，则在该点处的切线方程为yy0=p(x+x0).

公式四：若点P(x0,y0)在抛物线x2=2py上，则在该点处的切线方程为xx0=p(y+y0).

第一，虽然隐意处于所言与含意的中间层，但受语境影响，它的中介作用具有临时性。如果听话者的交际期待在隐意阶段得以实现，隐意成为最终交际意义，就不需要用进一步的语用加工来理解含意。

3.圆锥曲线的切线综合问题

( )

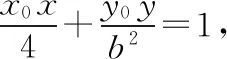
【评注】该题考查求椭圆的离心率，也考查求圆锥曲线的切线方程，是中档题.如果考生熟悉椭圆和双曲线的切线方程，那么该题就可以被快速解决.

四.曲线的切线不等式问题

1.两个重要的曲线切线不等式

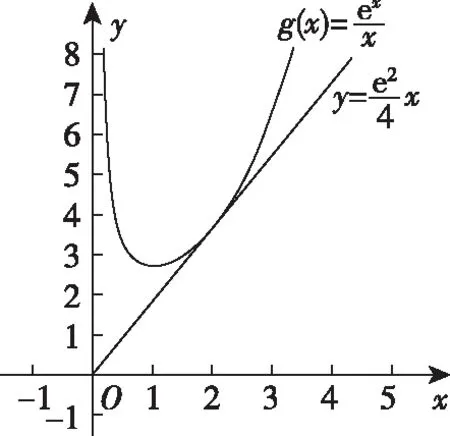
由于函数y=ex的曲线在x=0处的切线方程为y=x+1，并且曲线在直线的上方(如图所示)，则ex≥x+1(x∈R)，当且仅当x=0时等号成立.

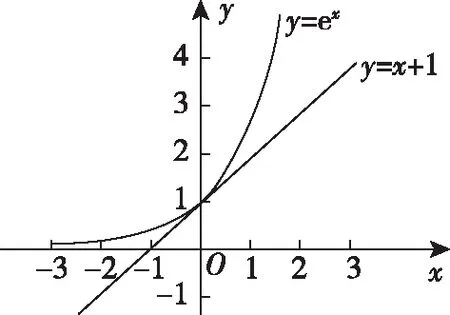
公式五：ex≥x+1(x∈R)，当且仅当x=0时等号成立.

证明：设f(x)=ex-x-1，则f′(x)=ex-1.因为当x>0时，f′(x)>0；当x<0时，f′(x)<0，所以f(x)min=f(0)=0，则当x∈R时，ex≥x+1，当且仅当x=0时等号成立.

由于函数y=lnx的曲线在x=1处的切线方程为y=x-1，并且曲线在直线的下方(如图所示)，则lnx≤x-1(x>0)，当且仅当x=1时等号成立.

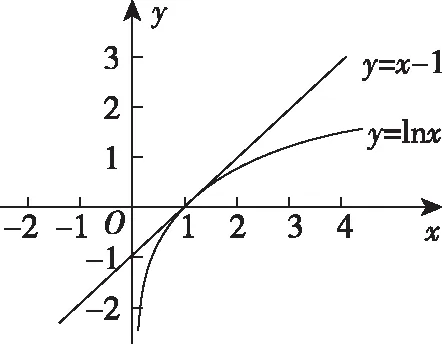
公式六：lnx≤x-1(x>0)，当且仅当x=1时等号成立.

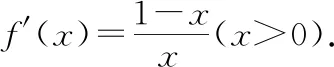
2.曲线切线不等式在解决数列综合问题中的应用

【例6】(2018·浙江卷·10)已知a1，a2，a3，a4成等比数列，且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1，则

( )

A.a1a3,a2

C.a1a4D.a1>a3,a2>a4

解析：因为lnx≤x-1，所以a1+a2+a3+a4=ln(a1+a2+a3)≤a1+a2+a3-1，得a4≤-1，即a1q3≤-1，所以q<0.若q≤-1，则a1+a2+a3+a4=a1(1+q)(1+q2)≤0，a1+a2+a3=a1(1+q+q2)≥a1>1(矛盾).所以-10，a4-a2=a1q(1-q2)<0.所以a1>a3，a2

【评注】该题为2018年浙江卷第10题，是数列与不等式的综合问题，也是难度比较大的试题.考生如果熟练掌握曲线的切线不等式lnx≤x-1，那么自然可以由a1+a2+a3+a4=ln(a1+a2+a3)看出a4≤-1，这就是该题的解题突破口.

3.曲线切线不等式在解决导数与不等式的综合问题中的应用

【例7】(2018·全国卷Ⅰ文·21)已知函数f(x)=aex-lnx-1.

(Ⅰ)设x=2是f(x)的极值点,求a，并求f(x)的单调区间；

4.曲线切线不等式在解决导数与函数零点综合问题中的应用

【例8】(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2.

(Ⅰ)若a=1，证明：当x≥0时，f(x)≥1；

(Ⅱ)若f(x)在(0,+∞)只有一个零点，求a.

解析：(Ⅰ)略；

【评注】该高考试题第(Ⅱ)小题是“导数与函数零点”的综合问题，常规的处理方法是：利用导数研究函数的单调性，得知函数的大致图象，分析函数图象与x轴交点的情况，进而得出参数的取值范围.可是，笔者在处理该题的过程中发现，灵活应用“曲线切线不等式”也可以解答该题，也就是说，“曲线切线不等式”为该题的解答开拓了新途径.