基于超统计理论的高速铁路跨线列车晚点分布模型研究
2019-08-02胡思继段清亮
袁 强, 武 旭, 胡思继, 段清亮
(1.北京交通大学交通运输学院, 北京 100044;2.中国铁路济南局集团有限公司济南调度所, 山东济南 250001)
高速铁路列车跨线运行是我国高速铁路网常见的客运组织方式,承担不同客运专线之间的客流输送。因高速铁路跨线列车具有便捷旅客出行、减少换乘次数、缩短旅行时间、服务质量高等优点,受到广大旅客的青睐。为满足跨线客流的运输需求及充分利用高速线的运输能力,我国高速铁路采用“高速线上本线列车和跨线列车共线运行”的运输组织模式,即高速线路上除了运行本线高速列车外,还运行一定比例的由衔接车站接入的跨线列车。本线列车和跨线列车共线运行的运输组织模式在实现客流运输直达性、减少旅客换乘问题的同时,对高速铁路的行车组织造成了一定影响。文献[1]研究表明,从天津站、济南站、徐州站接入京沪高速线的跨线列车平均晚点概率分别为53.6%、37.2%、70.6%,跨线列车到达正点率不容乐观。在高速线负荷较高时,跨线列车进入高速线晚点较多,必将产生列车运行之间的冲突[2]。在繁忙干线上,如果在运输过程中不能有效地控制晚点传播,将会造成大规模的连带晚点,影响高速线正常行车,对时效性要求很高的高速铁路运营造成极大的负面影响。随着我国高速铁路网规模的扩大,跨线列车运行的比例将会越来越高[3]。从高速线客运质量提升的角度出发,铁路企业必须重视跨线列车的晚点问题,掌握跨线列车晚点分布规律,为研究列车晚点传播及优化运输组织等提供基础。因此,有必要对高速铁路跨线列车的晚点时长分布模型进行研究。
1 研究现状
列车晚点分布一直是国内外学者研究的问题。既有研究主要围绕普速铁路,基于实绩数据分析列车晚点、列车晚点分类等方面研究列车晚点问题。文献[4]总结出普速铁路列车晚点服从负指数分布。文献[5]运用数理统计分析的方法验证了列车晚点分布与负指数分布吻合。长期以来,国内外关于列车晚点分布模型的研究比较薄弱,且受限于难以获得列车运行实绩数据,学者们常假设晚点分布模型[6]进行理论分析。在基于列车实绩数据研究列车晚点方面,文献[7]基于京沪高铁一个半月的列车运行实绩数据,分析列车区间运行时间与发车晚点的关系,以及列车停站时间与到达晚点的关系。文献[8]基于高速列车实绩运行数据,绘制了高速列车晚点分布曲线。在科学研究中,分类研究是常用方法之一,通过分类将问题细致化和微观化。文献[9]基于英国普速铁路列车运行晚点数据,对所有列车晚点数据和各条线路列车晚点数据进行分类研究。文献[10]基于广铁集团高速列车运行实绩数据,对不同致因下的高速铁路列车初始晚点分布模型进行分类研究,但并未从本线和跨线角度对列车到达晚点进行分类研究。既有研究中,关于高速铁路本线和跨线列车晚点的分类研究较少,且既有的关于列车晚点分布的研究存在两个问题:一是列车晚点分布模型可以很好的拟合列车晚点数据,但无法解释该晚点模型产生的机理;二是既有的列车晚点分布研究都假设用于拟合的所有列车晚点数据都服从同一分布,但又没有通过任何拟合前的分析来保证同一分布的假设条件能够得到满足。因此,为解决以上问题,本文基于京沪高速铁路列车运行实际数据,从本线和跨线角度分类,使用超统计理论对跨线列车晚点的机理及晚点时长分布模型进行研究。
2 跨线列车晚点超统计理论模型
2.1 高速铁路跨线列车晚点时长分布与超统计理论
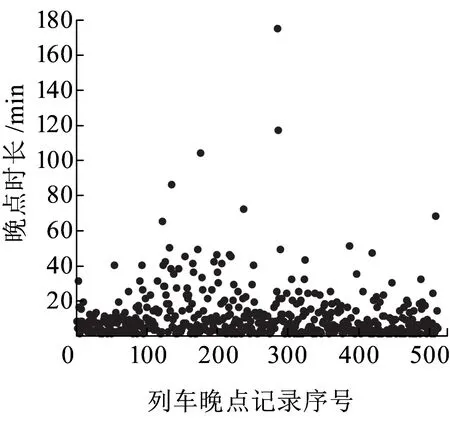
通常列车晚点是列车在运行过程中受到设备因素、环境因素和人为因素等方面的影响后逐渐累积的延迟。相比于本线列车,跨线列车受各种因素的影响更为显著。设T是跨线列车在运行过程中受到各种因素影响后到达晚点时长t的集合。集合T的时间序列如图1所示,从时间序列图中可以明显看出跨线列车晚点时长分布是一个复杂的非平稳随机过程,且存在异常晚点频繁出现的情况,较本线列车晚点情况复杂,对于具有此类特性的过程,可采用超统计理论建立分布统计模型[11]。

图1 跨线列车晚点时长序列
超统计理论[12](Superstatistics)是统计力学或统计物理学的一个分支,致力于研究非线性和非平衡系统,其特征在于使用多个不同的统计模型的叠加来实现期望模型的非线性[13]。目前,超统计理论已成为一个强大的工具来描述复杂系统,已经在物理学[14]、医学[15]、工程学[16]等复杂系统中得到广泛应用。超统计理论将复杂的非平衡系统现象模拟为两个随机变量的模型的叠加,一个对应相对微观的平衡系统,每个子系统(或者单元)内部平衡,且服从确定的概率分布;另一个对应缓慢变化的参数β,服从一定的统计分布f(β)。通过两层分布模型的叠加,得出整个复杂系统的分布模型。
当研究对象是整条线路的跨线列车到达晚点分布时,可以将该研究对象定义为一个宏观层的系统,那么该宏观层的系统包含若干个相对微观的单元(车站),每个车站都服从同一类型的分布模型,仅有环境参数的差异,该环境参数是随车站环境及宏观系统所处的路网环境的变化而缓慢变化的参数β,且服从一定的统计分布。因此,该宏观系统可以使用超统计理论来建模。对于单个车站,在较短的时间范围内,车站的环境参数β可以看作是一个定值,列车到达晚点服从一个确定的分布规律(负指数分布),此时这种状态为一种平衡状态。但在较长的时间尺度下,该参数不是固定不变的,是随时间变化而有所波动的。当车站环境或宏观系统所处的路网环境发生变化,原来的平衡状态被打破,变为紊乱的、有异常晚点值出现的现象,列车运行秩序偏离列车运行时刻表,产生了更为复杂的非平衡状态,这时就需要列车调度员采取适当的调整措施来使列车运行恢复正常。一段时间后,车站又重新达到一个新的平衡状态,环境参数发生改变,以此类推。将一个平衡态到另一个平衡态之间经历的时间记为τ,那么在较长的时间尺度T(T≫τ)上,由多个较小时间尺度的车站平衡系统组成该宏观层的跨线列车晚点复杂系统,如图2所示,该复杂系统可以使用超统计理论来建模。在超统计理论中,微观平衡系统建模是跨线列车晚点宏观系统建模的基础,因此首先以单个车站为研究对象,对微观平衡系统进行建模。
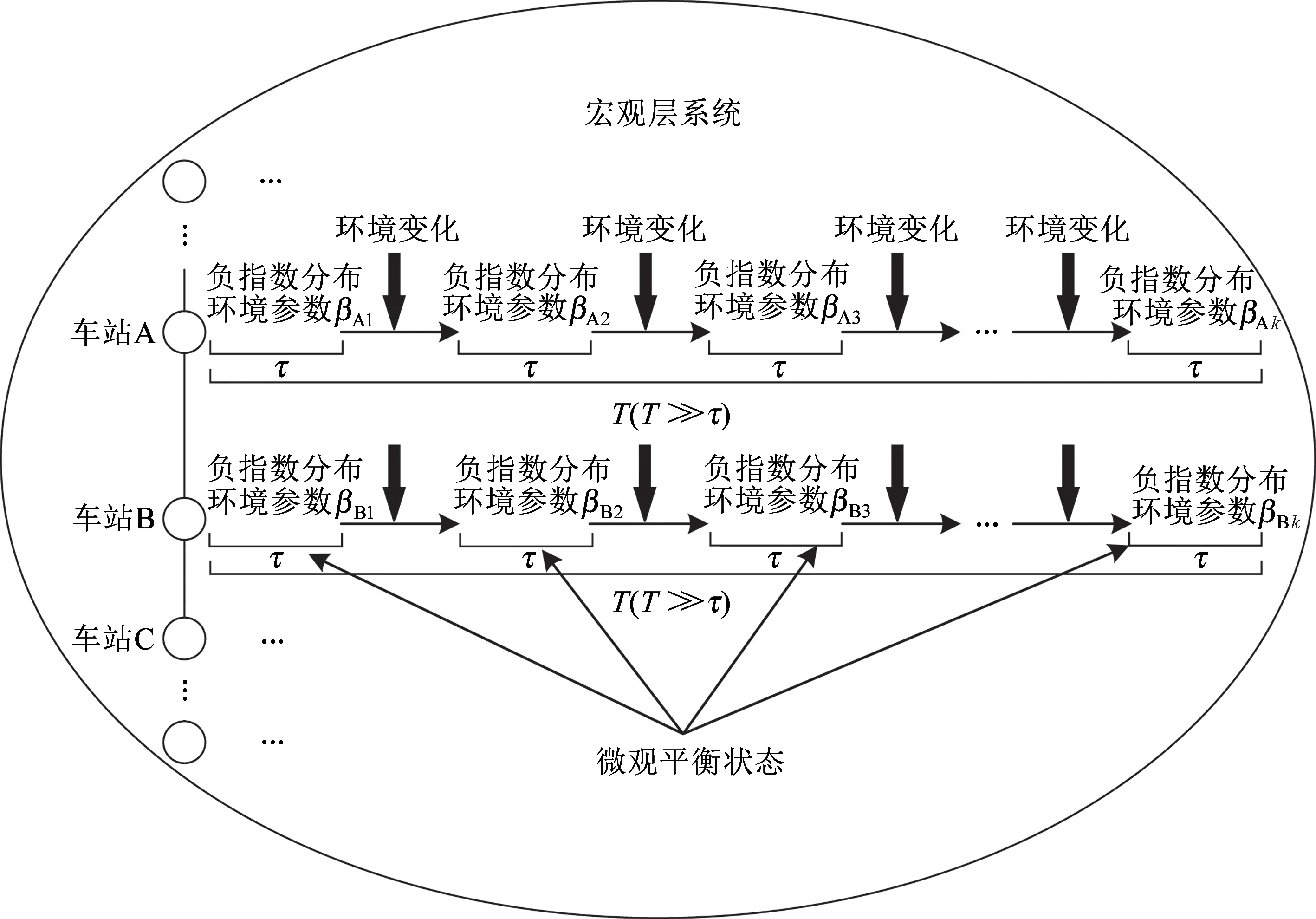
图2 宏观层跨线列车晚点复杂系统
2.2 微观系统建模
从微观角度,运用统计分析方法对单个车站跨线列车到达晚点时长进行分析,在正常情况下,列车的到达晚点时长分布可以用负指数分布很好地描述[17],给定车站环境参数的条件概率分布为
P(t|β)=βe-β t
(1)
式(1)为较短时间尺度内微观平衡系统的列车晚点分布模型。t表示列车实际到达时刻与图定到达时刻之差,即列车晚点时长(单位:min)。P(t|β)表示短时间内单个车站在环境参数β给定的条件下,列车晚点时长t的概率密度。β是短时间内的车站环境参数,是一个受车站设施设备、车站的运营环境(车站突发事件、车站工作人员罢工)、线路设备故障、恶劣天气、暑期客流等方面综合影响的正值参数,且该参数具有时空不均匀性,即同一时间段的不同车站或同一车站在不同时间段的平衡状态下的环境参数有所差异。车站环境参数β可由该车站对应时间尺度内的列车晚点数据拟合进行确定。
列车到达晚点分布始终遵循“小晚点,大概率;大晚点,小概率”[18]的原则。不同环境参数β下的列车晚点分布曲线如图3所示,对于给定的晚点时长t,β值越大,列车发生较大晚点值的概率越小,意味着大多数跨线列车能够较及时地到达车站,反之β值越小,表示列车发生较大晚点值的概率变大,到达车站的列车平均晚点值增大。

图3 不同环境参数的列车晚点分布曲线
2.3 宏观系统建模
时间维度上,单个车站的环境是随时间推移而不断变化的,由于波动的环境参数β的存在,使得长时间尺度的单个车站的列车到达晚点分布模型为叠加统计变量分布模型;空间维度上,不同车站环境各异,这些环境差异最终都反映在各个车站波动的环境参数上。对于整条高速线路的跨线列车到达晚点分布,虽然不同车站有环境参数的差异,但都服从同一类型的分布模型,因此用第二层模型描述空间和时间两个维度的环境参数β的概率分布,用f(β)表示。那么在长时间尺度上,宏观层跨线列车晚点分布模型为两层模型的叠加。故高速铁路跨线列车到达晚点的边际分布为

(2)
构建第二层模型f(β),Xi(i=1,2,3,…,n)为n个不同的高斯随机变量,可以将环境影响的波动参数β看成来自不同影响因素Xi的累积,则有
(3)
假设这些影响因素相互独立,并且服从均值为0的正态分布,则β服从自由度为n的2-分布。
(4)
β0为波动参数β的均值,计算公式为
(5)
将式(1)、式(4)带入式(2),得到高速铁路跨线列车晚点的边际分布为

(6)
p(t)~(1+b(1-q)t)1/(1-q)
(7)
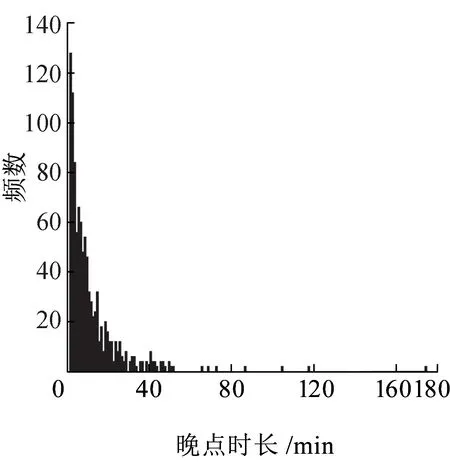
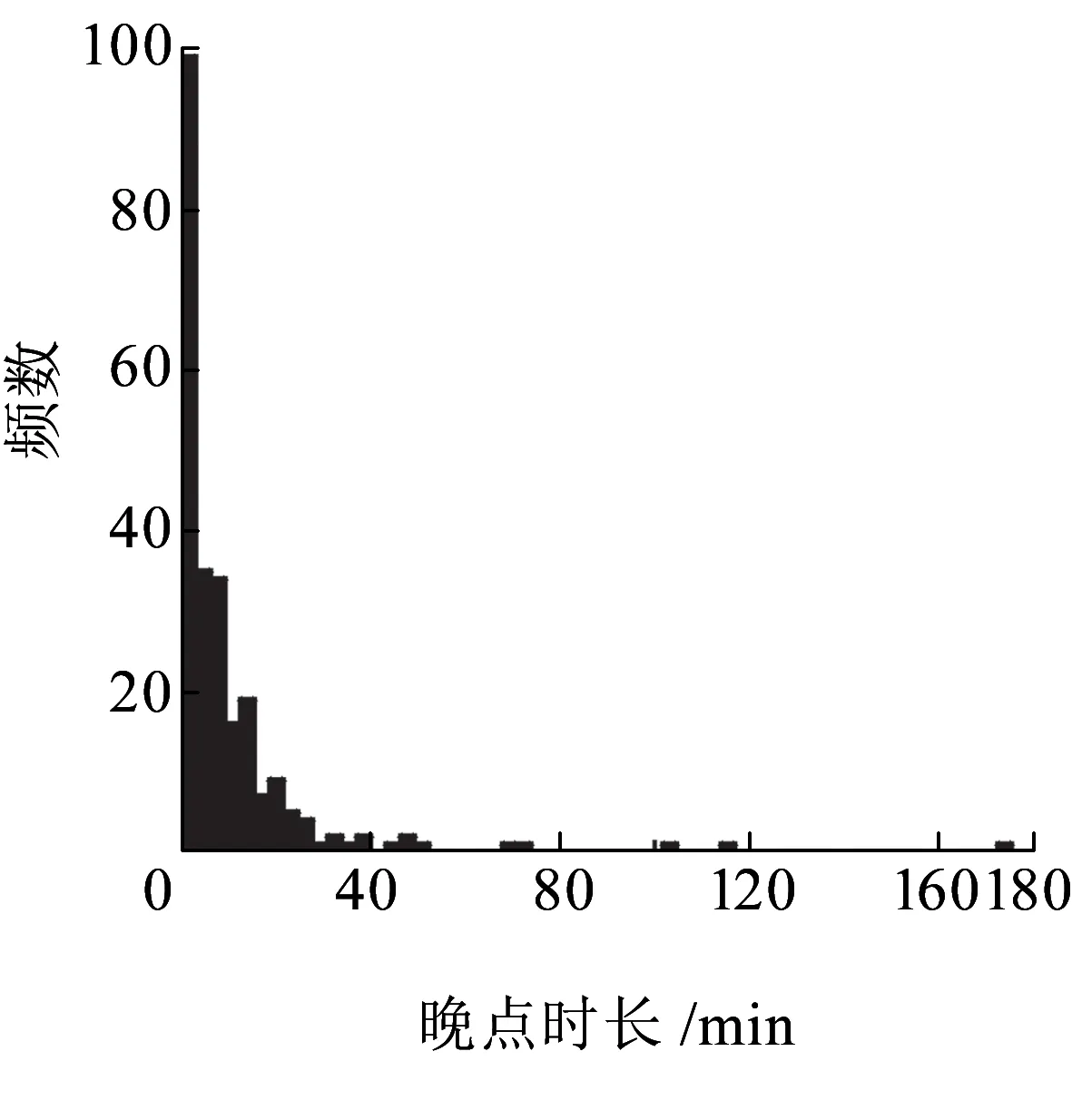
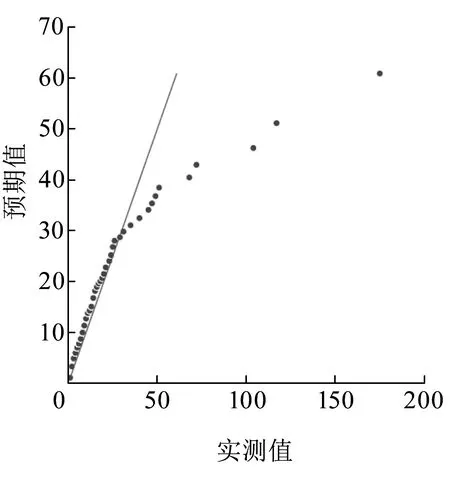
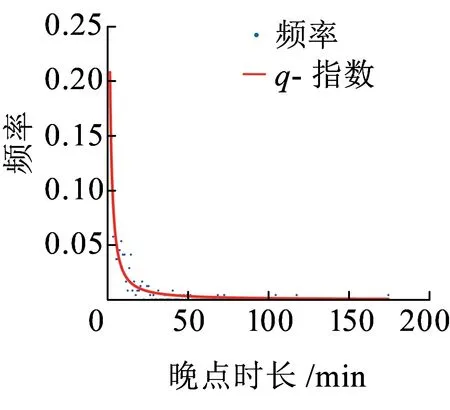
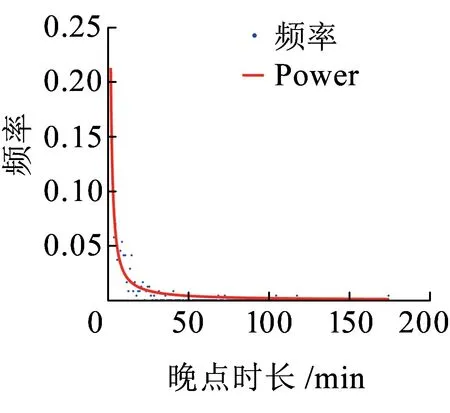
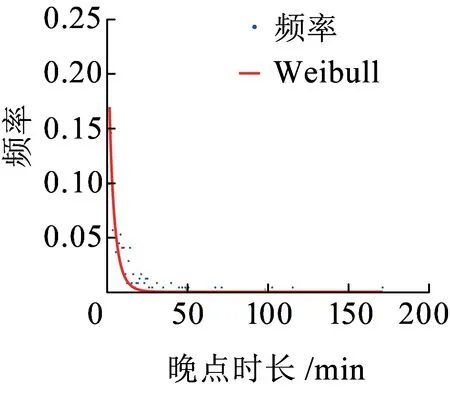
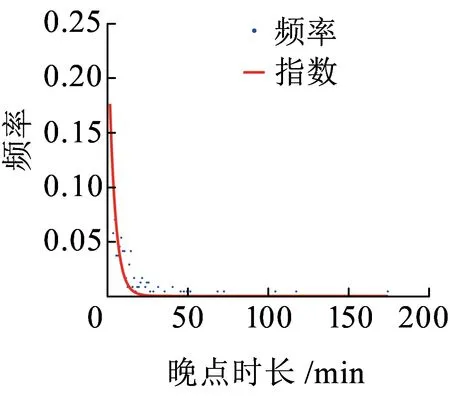
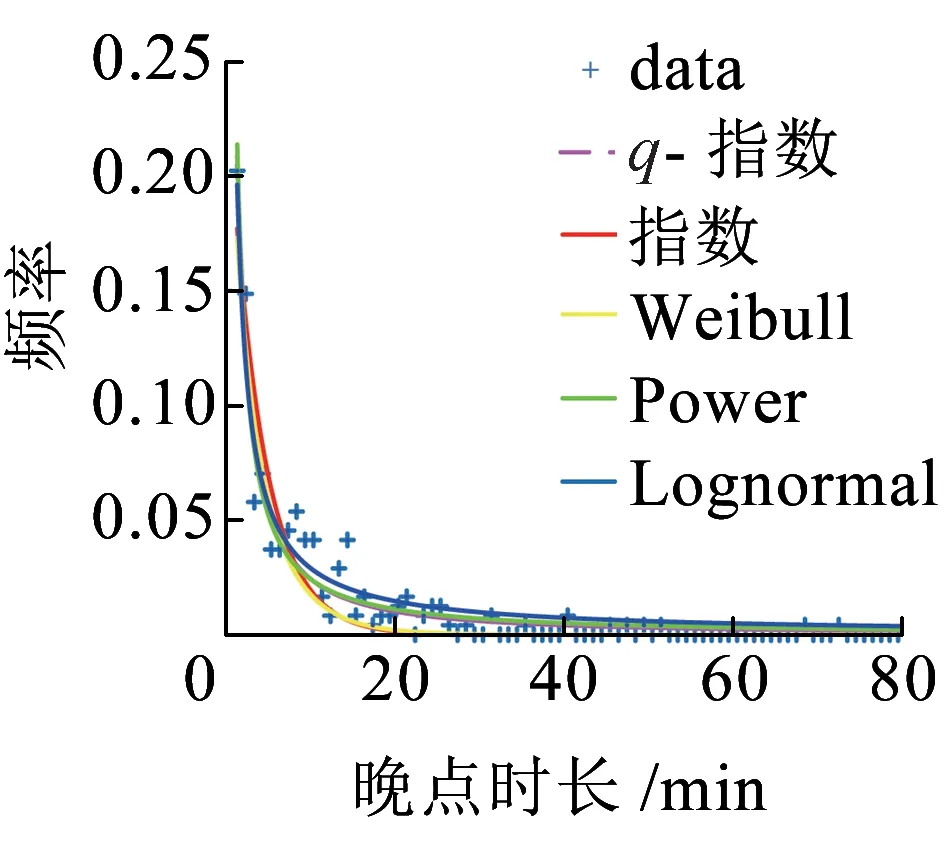
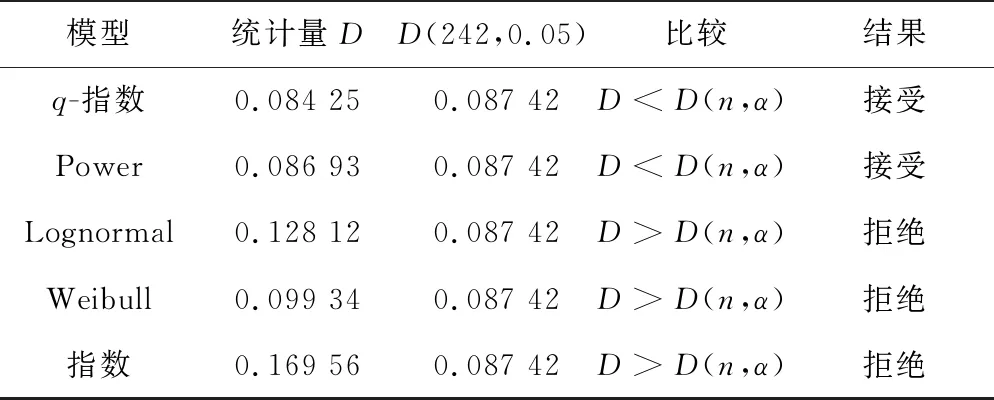
在复杂宏观系统的建模过程中,运用超统计理论的思想,从列车晚点机理中产生了跨线列车晚点时长分布的q-指数分布模型,见式(7)。q-指数函数是非广延热力学中常用的一种变形函数,最早由Tsallis[19]提出,因此也被称为Tsallis统计量。q-指数函数被定义为eq(x)=(1+b(1-q)x)1/(1-q),是一个正偏态分布函数,其中1+b(1-q)x≥0,q是熵指数[20],1 图4 不同熵指数q的q-指数分布概率密度函数 本文的列车运行实绩数据来源于铁路客户服务中心(12306网站)。从12306网站获取2018年9月1日—2018年9月30日京沪高速铁路各站的列车图定到达时间、实际到达时间等基本信息,经过数据处理后得到京沪高速铁路列车晚点时长数据。京沪高速铁路列车晚点时长散点图如图5所示,横坐标为9月1日—9月30日京沪高速铁路列车到达车站的晚点记录序号,纵坐标为列车晚点时长,由列车晚点时长散点图可以看出京沪高速铁路列车晚点数据在较小的晚点时长附近有较强的密集性,同时也存在较大的晚点值区域20~60 min和晚点异常值区域60~180 min。图6是京沪高速铁路列车晚点时长以1 min为间隔的频数分布直方图,横坐标表示列车晚点时长,纵坐标为晚点时长出现的频数,列车晚点最大值为175 min,最小值为1 min。 图5 京沪高速铁路列车晚点时长散点图 图6 京沪高速铁路列车晚点时长直方图 从京沪高速铁路列车晚点时长样本数据中筛选出京沪高速铁路跨线列车晚点数据,进行跨线列车晚点数据的分布特性及模型研究。京沪高速铁路跨线列车晚点时长直方图如图7所示,比较京沪高速铁路列车晚点时长直方图和跨线列车晚点时长直方图可以看出,京沪高速铁路列车晚点的异常值很大程度来源于京沪高速铁路跨线列车晚点数据。晚点异常值的出现使得跨线列车晚点分布具有厚尾性,且跨线列车晚点样本数据的峰度为43.15,标准正态分布的峰度等于3,43.15>3,表明跨线列车晚点时长分布具有“尖峰厚尾”性。跨线列车晚点数据的厚尾性可使用Q-Q图来检验。当被检验的数据符合所参照的分布时,Q-Q图中各点近似一条直线;若Q-Q图的上端右偏离该直线(向下倾斜),则表示被检验的样本数据相对参照的分布来说右尾具有厚尾性[22]。关于分布是否具有厚尾性一般都是与指数分布的尾部相比较而给予判断[23]。参照指数分布,跨线列车晚点时长数据的Q-Q图如图8所示,可以看出Q-Q图的中部较接近直线,但上端右偏离直线,向下倾斜,表明其尾端比指数分布的尾端要厚,即跨线列车晚点时长数据具有明显的尖峰厚尾特点。 图7 京沪高速铁路跨线列车晚点时长直方图 图8 跨线列车晚点时长数据Q-Q图 基于跨线列车晚点数据特征,结合超统计理论分析列车晚点机理建立了q-指数分布模型后,还需对模型的拟合优度和精度进一步检验。 由京沪高速铁路跨线列车晚点时长直方图(图7)的分布形状及其分布特性检验结果可以判断出跨线列车的晚点分布曲线具有正偏态、尖峰厚尾的分布特征,即频数分布的峰度较高且向左偏移,长尾向右侧延伸并存在幂律的渐近衰减。依据直方图外轮廓曲线与总体的概率密度函数曲线接近的原理及概率统计相关理论可知,符合正偏态、尖峰厚尾分布规律的分布函数包括Weibull分布、Lognormal分布、Power分布等。对跨线列车晚点时长样本数据进行非线性回归拟合,以拟合优度R-square作为模型选择的标准,分别对q-指数分布、Power分布、Lognormal分布、Weibull分布及常用于建模普速铁路列车晚点的指数分布等5个模型进行对比,跨线列车晚点数据拟合情况如图9所示,图中的蓝色点为跨线列车晚点时长样本数据,横坐标表示跨线列车晚点时长,纵坐标表示对应晚点时长的频率,不同分布模型的拟合优度数值结果见表1。 (a)q-指数分布模型拟合 (b)Power分布模型拟合 (c)Lognormal分布模型拟合 (d)Weibull分布模型拟合 (e)指数分布模型拟合 (f)5类分布模型拟合图9 非线性回归拟合 曲线拟合的优劣可以用误差平方和、均方根误差、拟合优度R-square来衡量。误差平方和、均方根误差越小,越接近0,R-square越接近1,表明曲线拟合效果越好[24]。通过比较拟合优度的数值结果发现q-指数模型、Power模型、Lognormal模型、Weibull模型、指数分布模型都有较大的R-square值,均具有较好的拟合优度,其中q-指数分布模型的拟合优度最佳。 表1 跨线列车晚点数据非线性回归拟合结果 在进行跨线列车晚点时长样本数据的非线性回归拟合时,以上5类分布模型都具有较大的R-square值,虽然R-square值较大,但模型的精度是否可行还需通过假设检验进行判断。常用的假设检验方法有卡方检验法和K-S检验法。卡方检验法是分区间来检验经验分布函数f(xi)与理论分布函数g(xi)之间的偏差,若采用卡方检验法对跨线列车晚点时长样本数据进行检验,需将晚点时长样本数据进行区间划分,统计区间内的实际频数与理论频数,并将理论频数不足5的区间进行合并处理,整个检验过程依赖区间划分,且当区间的实际频数与理论频数偏差较小时,并不意味着单个样本数据点的实际频数与理论频数偏差较小,即无法确定每个样本数据点的精确的拟合情况。与卡方检验法相比,K-S检验法不是分区间来计算偏差,而是对每个样本数据点都检验经验分布f(xi)与理论分布g(xi)之间的偏差,具有较高的精确性。因此,采用精确性较高的K-S检验法对京沪高速铁路跨线列车晚点数据进行假设检验。 K-S检验法的全称是Kolmogorov-Smirnov检验法,是一种非参数检验方法。该检验方法基于累积分布函数,用以检验一个经验分布f(xi)与另一个理论分布g(xi)是否相同或两个经验分布是否相同。分别将q-指数模型、Power模型、Lognormal模型、Weibull模型、指数模型作为理论分布,采用K-S检验确定模型的精度是否满足要求。以跨线列车晚点样本数据是否服从q-指数分布的K-S检验为例,设原假设H0:跨线列车晚点数据服从q-指数分布;备择假设H1:跨线列车晚点数据不服从q-指数分布。 表2 模型的Kolmogorov-Smirnov检验准确度 由计算结果可知,q-指数分布模型、Power分布模型与经验分布的最大偏差均小于K-S检验的临界值,因此接受原假设,从理论上讲,q-指数模型和Power模型都可以用来建模跨线列车晚点时长。但相比较Power分布模型,q-指数分布模型有较大的R-quare和较小的偏差。目前,随着高速铁路成网运营及高速线路客流的持续增长,我国部分高速铁路通过能力已处于十分紧张的状态,在这种线路能力紧张的状态下,列车晚点分布模型越精确,越有利于提高高速铁路运行质量分析的精度,同时也有利于提高高速铁路实际调度指挥及运行图铺画水平。因此,从跨线列车晚点分布模型的精确性及模型产生的机理角度综合考虑,q-指数分布模型eq,b,c(t)=(1+b(1-q)t)1/(1-q)作为跨线列车晚点时长分布模型较优。 采用非线性最小二乘法来估计京沪高速铁路跨线列车晚点时长分布模型中的参数q和b,得参数值q=1.191,b=-0.465 5。不同线路跨线列车晚点分布模型中的参数是有差异的,但参数确定的方法类似。实际中也可通过对比q值大小反映列车运行秩序的好坏,较小的q值表明列车运行秩序较好。 基于京沪高速铁路列车运行实绩数据,运用超统计理论,建立基于超统计理论的跨线列车晚点时长分布模型,得出如下结论: (1)当研究对象是整条线路的跨线列车到达晚点分布时,可以将其分析定义为一个宏观层系统,该宏观层系统包含若干个相对微观的单元(车站)。对于单个车站,在较短时间尺度内,列车到达晚点服从含有车站环境参数β的负指数分布,将其定义为微观平衡系统;在较长时间尺度下,车站环境是随时间推移而不断变化的,由于波动的环境参数β的存在,长时间尺度的单个车站的列车到达晚点分布为叠加统计变量分布模型。在空间维度上,不同车站环境各异,这些环境差异最终都反映在各个车站波动的环境参数上。因此,当研究对象是整条高速线的跨线列车到达晚点分布时,第一层模型为描述微观平衡系统的含有波动参数β的负指数分布模型,第二层模型为描述空间和时间两个维度波动的环境参数β的概率分布,那么在长时间尺度上,宏观层跨线列车晚点分布模型为两层模型的叠加。通过微观的平衡系统和波动参数两层分布模型的叠加,得出整个复杂系统的q-指数分布模型。 (2)以京沪高速铁路列车运行实绩数据为依据,对跨线列车晚点时长样本数据进行非线性回归拟合,以拟合优度值作为模型选择的标准,确定与京沪高速铁路跨线列车晚点样本数据较拟合的分布模型。数据拟合结果表明q-指数分布、指数分布、Weibull分布、Power分布、对数正态分布等5个模型都具有较好的拟合性。进一步使用拟合准确度为D0.05水平下的K-S假设检验法对具有较大拟合优度值的q-指数分布模型、指数分布模型、Weibull分布模型、Power分布模型、对数正态分布模型的精度进行检验。将模型的K-S检验结果结合目前高速铁路对列车晚点分布模型精确性需求,确定出使用q-指数分布建模高速铁路跨线列车晚点时长分布。 本文使用超统计理论分析跨线列车晚点时长分布规律,得到的跨线列车晚点分布模型不仅能够较好地拟合列车晚点数据,且模型产生的机理能够得到较好的解释。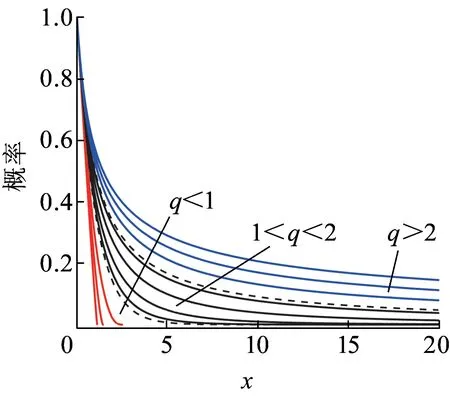
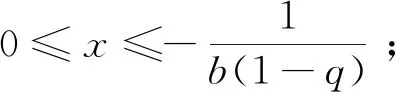
3 数据分析
4 q-指数函数的拟合优度与精度检验
4.1 非线性回归拟合


4.2 分布模型的K-S检验
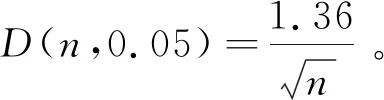
5 结论
