薄壁曲线箱梁空间振动分析方法

2019-08-01卢海林颜燕祥严若愚

铁道学报 2019年6期

蔡恒，卢海林，颜燕祥，严若愚

(1.武汉大学土木建筑工程学院，湖北武汉 430072；2.武汉工程大学土木工程与建筑学院，湖北武汉 430074)

薄壁箱梁广泛用于现代桥梁结构中。薄壁箱梁的空间受力比较复杂，在对称荷载作用下其基本变形包括竖向弯曲和剪力滞变形[1]；在偏载作用下，将会产生扭转和畸变效应[2-4]；对于薄壁箱形曲梁，由于存在曲率的影响，不论荷载是否对称，将会产生相互耦联的弯曲、扭转、翘曲、畸变和剪力滞变形，受力复杂。

文献[5-6]由刚度法原理推导各节点10自由度的直线箱梁空间单元刚度矩阵和刚度方程，考虑了约束扭转、畸变和剪力滞效应。文献[7]基于有限元理论提出同时考虑拉压、弯曲、扭转、翘曲、畸变、剪力滞效应及其交互作用的每节点14自由度的薄壁曲线箱梁空间分析单元刚度矩阵。文献[8]建立薄壁曲梁挠曲扭转分析的弹性控制微分方程组，考虑弯曲、扭翘、畸变和剪力滞效应，得到精确的解析解。文献[9]直接从壳体结构特点出发，由8 节点曲边四边形膜单元和基于Reinssner 中厚板理论的弯曲单元，推导考虑剪切闭锁效应的薄壁箱梁空间壳单元刚度矩阵及相应的刚度方程，以计算箱梁的剪力滞效应。可以看出上述研究完善了薄壁箱梁的静力分析理论。

近年来，为了满足大跨度桥梁结构抗风、抗震需要，学者们对箱形桥梁的动力特性也进行了研究。文献[10]由广义坐标法和能量原理推导曲线梁桥振动控制微分方程，给出显式刚度矩阵和质量矩阵，但未考虑畸变和剪力滞效应。文献[11]推导曲线桥地震分析的有限单元法，同样未考虑畸变和剪力滞效应。而现代大跨度PC箱梁桥施工时都不再设横隔板，使得刚性扭转和畸变产生的纵向翘曲应力会达到恒载和活载共同作用下纵向弯曲应力的24%～26%[12]。此外还存在剪力滞效应，剪力滞不仅造成箱梁肋板交界处应力集中，引起梁体局部开裂，还会削弱弯箱梁的刚度，引起附加挠度增大[13]。基于此，本文采用动力有限元理论，通过在节点位移中引入高阶位移插值函数，综合考虑薄壁曲线箱梁的拉压、弯曲、扭转、翘曲、畸变和剪力滞效应，推导每个节点的11自由度单元刚度矩阵和质量矩阵，求解薄壁曲线箱梁的振动频率和振型，并采用有限元软件ANSYS加以验证，为曲线箱梁桥的抗风和抗震研究提供依据。

1 单元刚度矩阵

1.1 基本假定

为简化薄壁曲线箱梁的空间力学模型，做如下假定：

(1)材料处于线弹性工作阶段；

(2)只在竖向弯曲中计入剪力滞变形；

(3)采用二次抛物线构造剪力滞翘曲位移函数；

(4)不计扭转翘曲、畸变和剪力滞三者之间小量耦联变形；

(5)薄壁曲梁截面尺寸相对于跨度和曲率半径是小量级的。

1.2 剪力滞效应

图1为薄壁曲梁示意图，以横向为x轴，竖向为y轴，纵向为z轴，单元节点位移可表示为

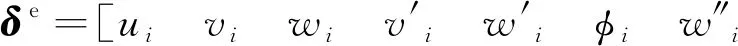
(1)

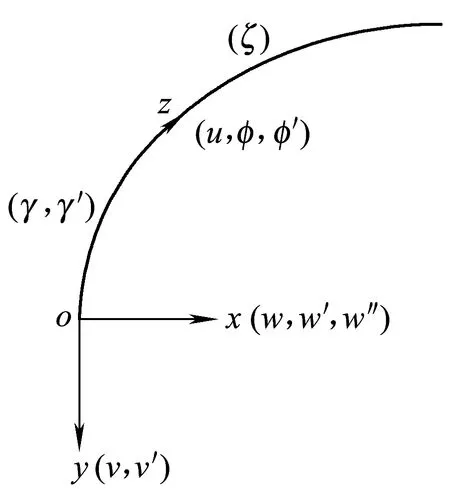
图1 薄壁曲梁示意

式中：i、j为单元节点编号；u、v、w分别为箱梁纵向、竖向和横向位移；v′、w′、φ分别为竖向转角、横向转角和扭转角；w″为横向曲率；φ′、γ、γ′分别为扭转翘曲、畸变和畸变翘曲位移；ζ为翼板剪切位移最大差值。ζ对于考虑剪力滞效应是必要的，按照假定(3)，剪力滞翘曲位移函数表示为

顶板：

(2)

底板：

(3)

悬臂板：

(4)

则箱梁纵向剪力滞翘曲位移可表示为

ξ(x,z,t)=ω(x)ζ(z,t)

(5)

式中：h1、h2分别为形心O到顶板、底板壁厚中线的距离；b1、b2分别为顶板宽度的一半和翼缘板宽度，如图2所示。

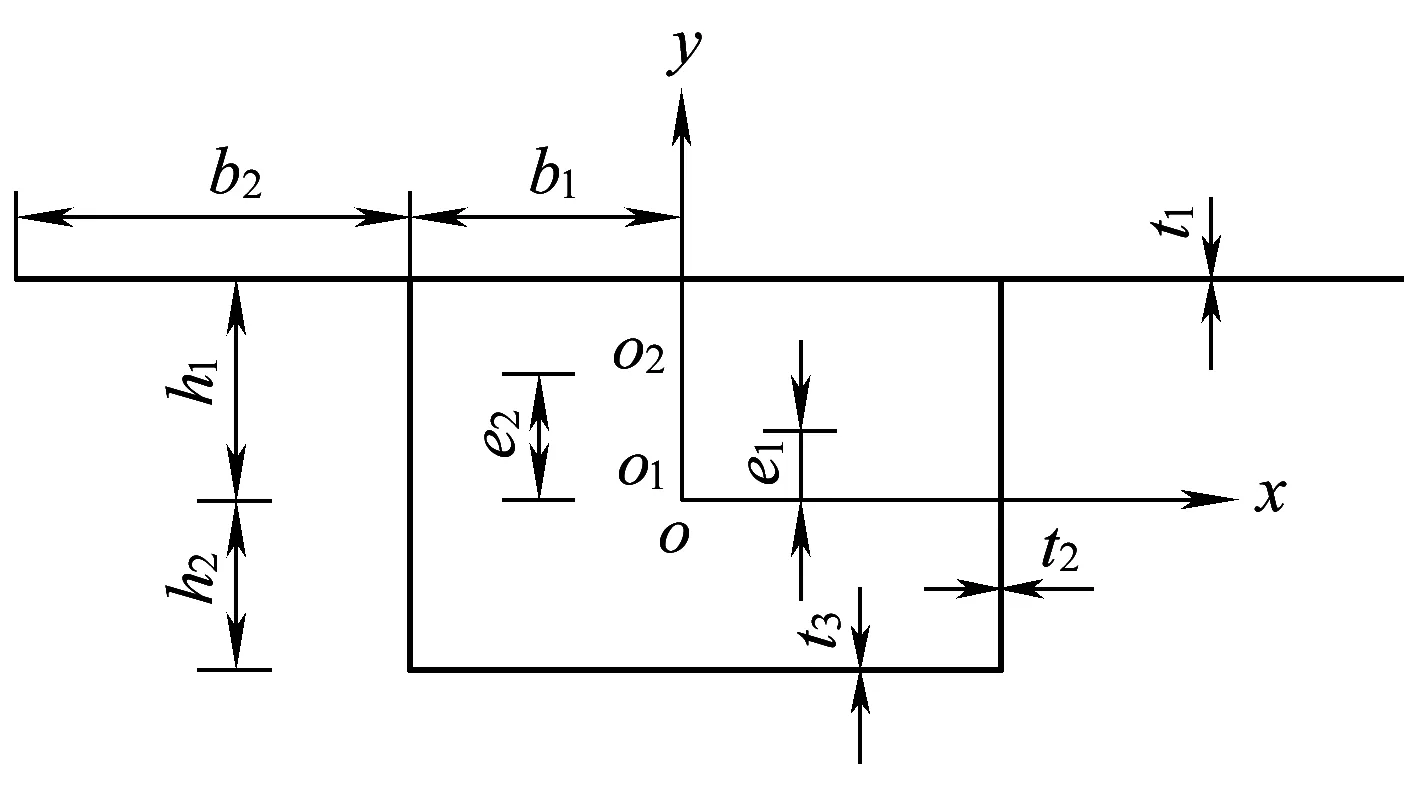
图2 曲线箱梁截面

图2中，O1为扭转中心，其到形心的距离记作e1；O2为畸变中心，是指只发生畸变而无其他位移时，各周边切向分量对应的转动中心，其位置可由文献[14]确定，畸变中心到形心的距离记为e2。

1.3 刚度矩阵

根据弹性力学几何方程，薄壁曲线箱梁广义应变可表示为

(6)

写成矩阵形式为

(7)

式中：等号右边第一项为微分算子，记作P；等号右边第二项为箱梁任一点的广义位移列阵，记作δ；则式(7)可表示为

ε=Pδ

(8)

由文献[15]，假设横向位移按五次多项式插值，竖向位移和扭转角按三次多项式插值，轴向位移按一次多项式插值，这4个插值与式(1)节点位移是相对应的，可以得到位移形函数矩阵

(9)

式中：N1～N12为位移插值函数，具体可表示为

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

式中：l为单元长度；z为插值点的长度。

因此，单元内任一点位移可表示为

δ=Nδe

(22)

式中：δe为单元节点位移矩阵。将式(22)代入式(8)中，得到

ε=PNδe

(23)

令B=PN，则ε=Bδe，B称为应变矩阵，薄壁箱梁的弹性矩阵可表示为

(24)

式中：E、G分别为弹性模量和剪切模量；Ix、Iy分别为箱梁截面对x轴和y轴的惯性矩；Id、Iw分别为自由扭转惯性矩和翘曲扭转惯性矩；IR、Ir分别为畸变框架惯性矩和畸变翘曲惯性矩。

单元内任一点应力可表示为

σ=Dε=DBδe

(25)

令S=DB，则σ=Sδe，称S为应力矩阵。

根据虚功原理，单元内任一点虚应变为

ε*=Bδ*e

(26)

单元内应力在虚应变上做的功为

(27)

杆端力在虚位移上做的功为

δW2=δ*eTFe

(28)

由δW1=δW2，得到

(29)

单元的刚度矩阵为

(30)

将应变矩阵B和弹性矩阵D代入式(30)，可得单元刚度矩阵K的表达式为

(31)

2 单元质量矩阵

根据图2，考虑到质心与扭心、畸心不重合，由牛顿第二定律，箱梁任一点横向惯性力为

(32)

式中：ρ为箱梁的密度；点表示对时间t的导数。

同样由于偏心，横向惯性力会引起附加扭矩和附加畸变矩，扭转惯性力矩和畸变惯性力矩分别为

(33)

(34)

式中：Iρ为箱梁极惯性矩。箱梁任一点惯性力为

(35)

写成矩阵形式

(36)

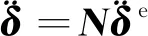
(37)

等效节点力为

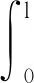
(38)

将式(37)代入式(38)中，有

(39)

由此可得质量矩阵为

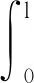
(40)

式中：l为曲线箱梁跨径(单元长度)，将M写成矩阵形式

(41)

3 振动频率方程

把薄壁曲梁沿z轴方向划分为若干个单元，每个单元有2个节点i和j，每个节点有11个自由度，如图3所示。

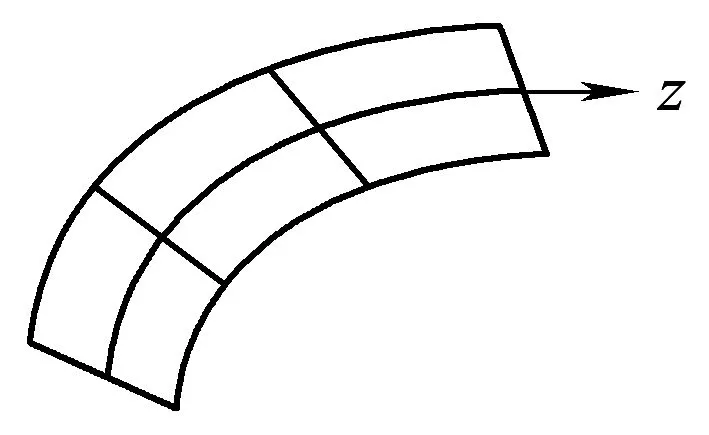
图3 薄壁曲线箱梁离散元

将单元刚度矩阵和质量矩阵按对号入座法则进行组装形成总刚度矩阵、总质量矩阵。本文采用流动圆柱坐标系，故不需要对薄壁曲梁进行坐标转换。

薄壁曲梁的振动方程为

(K-ω2M)δe=0

(42)

式中：ω为振动频率，当薄壁曲梁发生自由振动时，式(42)有非零解，故有

K-ω2M=0

(43)

根据式(43)，引入相应的边界条件，便可以求得薄壁曲梁振动频率。

4 算例

以文献[12]薄壁简支箱梁为例，截面尺寸如图4所示，跨径为40 m，计算过程中认为它是曲线梁，即不改变截面尺寸、边界条件和跨径，按曲率半径R=100 m的曲线梁考虑。

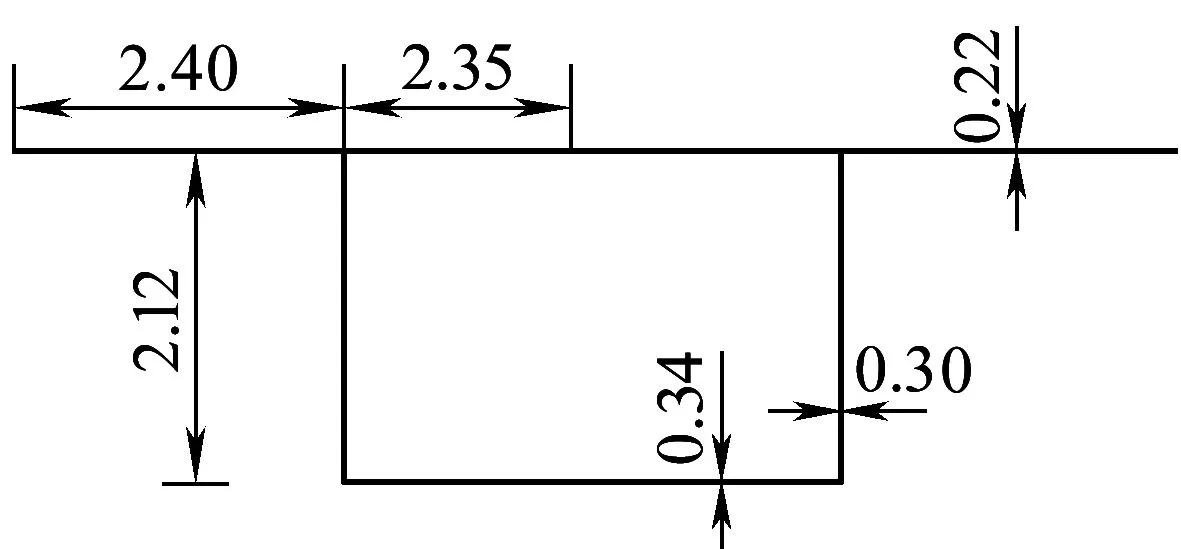
图4 箱梁截面尺寸(单位：m)

将薄壁曲线箱梁沿轴向划分为3个单元，采用MATLAB编制计算程序求解特征值方程。由于ANSYS中的Beam188梁单元不能反映结构的扭转振动特性，故采用Shell63单元建立有限元模型，在腹板与底板交界处结点施加约束，两端约束Ux、Uy、Uz。在结构的动力分析中，主要考虑低阶模态，故取前5阶自振频率，结果见表1。

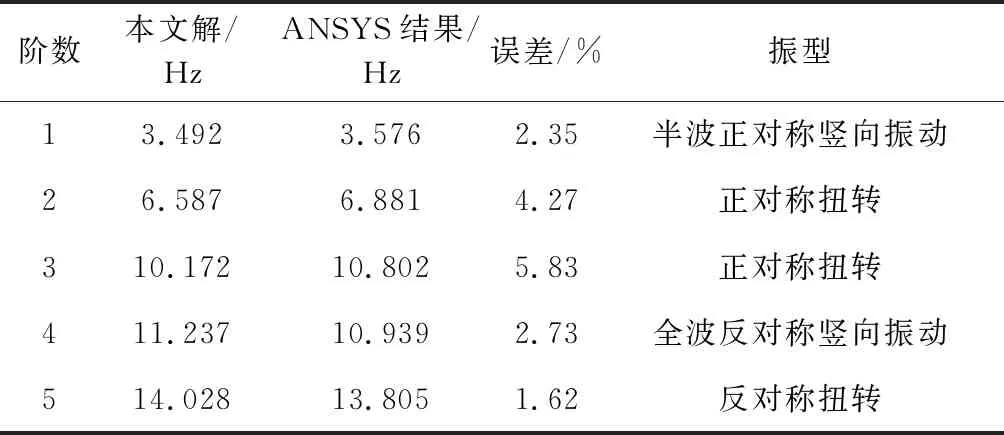
表1 简支曲线箱梁自振频率

注：误差=|本文解-ANSYS结果|/ANSYS结果。

由表1可以看出，本文解与ANSYS结果存在一定的误差，主要是因为在ANSYS中约束位于梁端腹板与底板交界处的结点，而理论计算中约束的是截面的中心，二者边界条件约束存在差异，但误差大部分不超过5%，理论计算结果与ANSYS有限元结果吻合良好，表明本文所构造的薄壁曲线箱梁单元刚度矩阵和质量矩阵是正确可靠的。此外，当曲率半径R趋于无穷时，便可计算直线箱梁的自振特性，所提出的方法具有通用性，优于以往仅能计算直线箱梁自振特性的方法，限于篇幅，不再举例说明。