基于周期控制的载波移相策略研究

张馨予，张 钢，刁利军，钱江林，刘志刚

(1.北京交通大学电气工程学院，北京 100044; 2.北京市轨道交通电气工程技术研究中心，北京 100044)

随着中国高速铁路的发展，高频谐波问题越来越受到人们的关注，并且国内外多次发生由于机车高次谐波注入牵引网而引发的车-网高频振荡事故。如1995年瑞士，发生牵引网高频振荡，使得列车不能正常运行；2007年京哈线，在“蓟县南”牵引变电所的供电区段发生了强烈的高频振荡事故，导致变电所不能正常工作；2011年京沪线，牵引网与高速列车牵引传动系统高频耦合振荡，导致列车不能正常运行[1]。这些事故均由机车内部四象限变流器产生的高次谐波在电网中引起高频振荡所致，这些事故不仅会给旅客带来不便，还会给铁路带来一定的财产损失。 因此，减小机车产生的高次谐波可以在一定程度上降低车-网高频振荡的风险，是一项十分有意义的工作。

目前国内外高速列车普遍采用载波移相的控制策略减小高次谐波[2-3]，为了保证各动车上牵引变流器之间载波移相角固定不变, 传统方案是采用硬线进行同步，但这种方式不利于牵引变流系统的生产和维护，更不利于列车任意编组重联运行时的谐波对消。对于载波移相策略的研究，国内外学者将其应用于多种领域。文献[4]将载波移相SPWM调制策略应用于牵引变电所中，并利用双边傅里叶函数推导了载波移相SPWM调制策略下的级联牵引变电所输出电压谐波特性，提供了一种基于载波移相策略的谐波分析及计算方法。文献[5]介绍了载波移相SPWM控制策略，该控制策略可以实现对多电平变换器功率单元直流电容电压良好的稳压和均衡控制效果。国内外学者也将载波移相策略应用于牵引变流系统中，但很少有关于不同四象限变流器在运行过程中载波移相角发生偏移的相关报道。文献[6]介绍了一种基于DSP和FPGA的载波移相策略实现方法，主要是对DSP和FPGA在处理载波移相的工作流程进行介绍。文献[7]介绍了一种具有抑制直流侧电容电压波动的载波移相策略，该策略与传统的载波移相策略相比，具有输入电压和电流谐波低的特点，但文中没有考虑多编组列车变流器之间载波移相角的同步。文献[8]从理论上详细分析了载波移相的原理，为载波移相SPWM调制策略提供了合理的分类，并分析了全范围移相角对谐波的影响，但未提及载波移相角的校正问题。

本文在国内外载波移相技术研究的基础上，提出一种基于周期控制的载波移相策略，该方法考虑了列车在运行过程中载波移相角的变化，并且该方法不需要在变流器之间设置同步线来校正移相角，只需检测网压过零点，通过微调PWM载波周期，即可实时校正载波移相角，可以更好地实现载波移相的功能，简单方便，运行稳定。从理论计算方面介绍载波移相的原理，介绍了基于周期控制的载波移相策略的实现方法，通过仿真和实验来验证该方法的可行性和有效性。

1 基于载波移相的谐波对消原理

以一台牵引变流器，两个四象限变流器模块为例，分析基于载波移相的谐波对消原理。假定网压的初相角为0°，网压角频率为ωs，有效值为UN，则网压uN可以表示为[9-10]

(1)

在控制作用下，网侧电流的基波分量is1与网压uN同频率同相位，设其有效值为Is1，即有

(2)

uL1为电感电压的基波分量，uab1为交流端电压的基波分量，Ls为网侧电感值，则各电压的基波分量满足

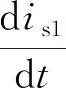
(3)

根据交流电流基波分量与网压uN同相位，可得

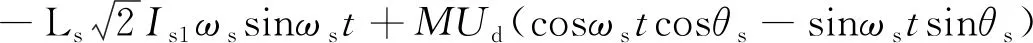
(4)

式中：M为调制比；Ud为直流侧电压；θs为调制波的相位偏移角。

从而可以进一步推导出四象限变流器模块1的电流幅值为

(5)

根据双变量控制波形的傅里叶基本表达式可得[11-12]

(6)

式中：θc为载波的相位偏移角；m为载波倍数；n为调制波倍数。

同理可以表示出四象限变流器模块2的电流is2，从而计算出两个四象限变流模块电流之和is。

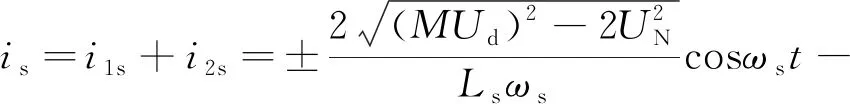
(7)

由于采用载波移相策略，因此两个载波之间的夹角为90°，化简式(7)可得

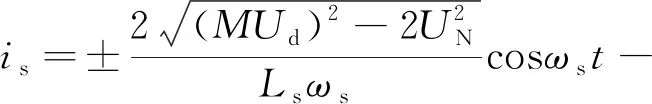
(8)

两个四象限变流模块经过载波移相后，当载波倍数m不是4的倍数时，它所对应的载波频带及其边带谐波被全部消除；当载波倍数m是4的倍数时，对应的载波频带及其边带谐波才有值。载波移相相当于将二电平载波频率变为原来的2倍，总的输出电压谐波分布在等效载波角频率的2倍及2倍上下边带上。载波移相策略在不提高各单相桥开关频率的前提下大幅降低了交流开关次谐波含量，适合在多重化级联的牵引变流系统中使用[13]。载波移相策略同样适用于多个四象限变流模块的情况。

2 基于周期控制的载波移相策略

2.1 载波同步策略

由于不同变流器之间没有同步线连接，所以不同四象限变流器桥臂之间的载波移相角不定，即使在变流器运行前设定移相角度，但不同控制板中的晶振不同，在计时上有所偏差，长时间运行会导致移相角变化，不能达到固定移相角，从而抑制开关次谐波，因此载波同步策略显得十分重要。

由于不同变流器之间只有网侧电压是相同的，所以采用网压Uac作为同步信号，但Uac是正弦交流信号，不易选取不同变流器之间同步的基准点，所以将网压信号Uac输入到硬件同步电路中，经过电压比较器，将正弦交流信号转化为方波同步信号，再用DSP中的ECAP模块来捕捉方波的上升沿，并产生中断，从而进入中断进行不同变流器之间的同步，如图1所示。并且ECAP内部有一个计数器，它可以记录产生中断到载波移相程序实际执行的时间，这样就可以更准确地得到载波周期修正量，从而精确移相校正角度。

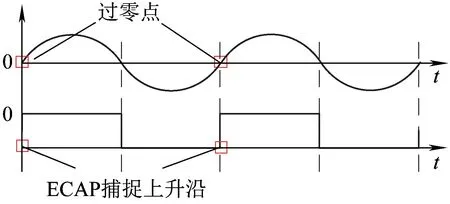
图1 方波示意图

2.2 基于周期控制的移相角校正

在四象限变流器发脉冲之前，通过设定载波移相寄存器的方式，将各个模块的移相角度设定好；在四象限变流器发脉冲之后就不能随意修改寄存器的值，防止在运行过程中载波相位突变，而引起交流电流不稳定。以混合动力动车组为例：三编组，两动一拖，共两台变流器，每个变流器里有两个四象限变流模块，移相角度分别为0°、90°、45°、135°，利用图2分析基于周期控制的移相角校正策略。

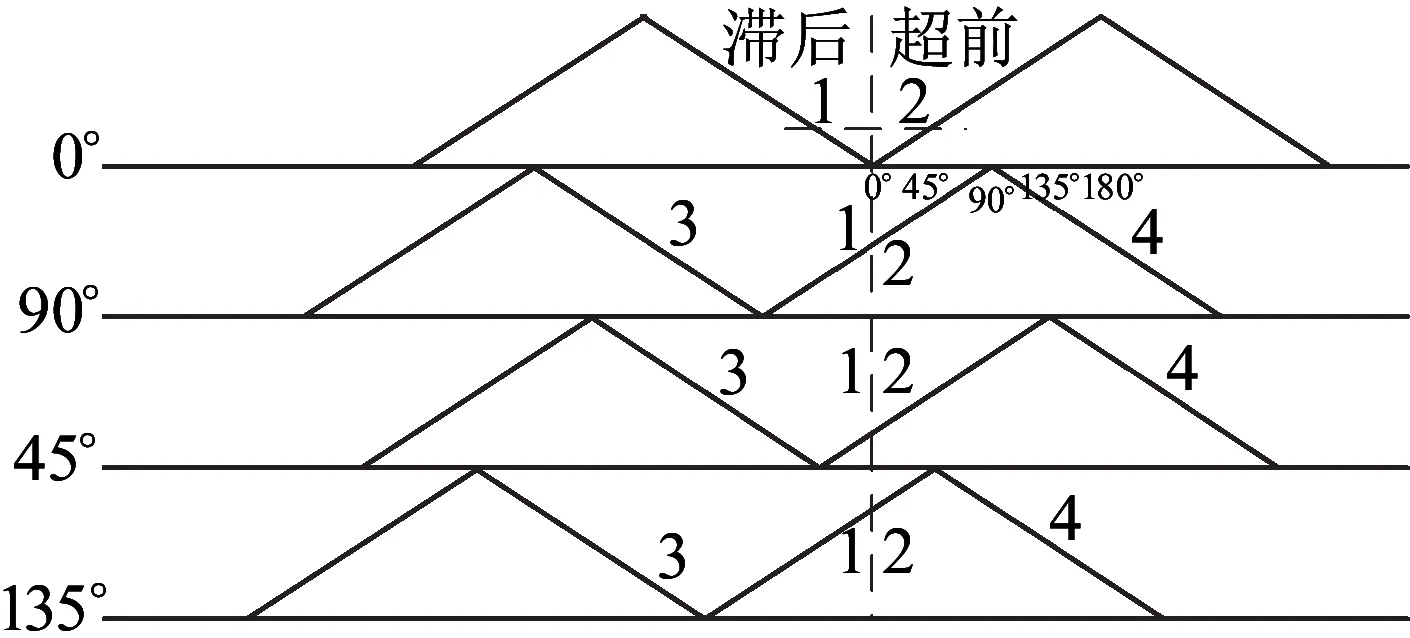
图2 周期控制的移相角校正策略示意

相位修正采用周期控制的方法，以工频为一个周期。混合动力动车组四象限变流器采用1 kHz的开关频率，在一个工频周期中有20个载波，每个工频周期期间，载波的误差相位需要平均分配到这20个载波中，通过修改这20个载波的周期达到修正并固定载波相位的目的。

如图 2所示，在四象限变流器发脉冲前将各个载波的相位固定在0°、90°、45°、135°，发脉冲后由于不同变流器内的控制板晶振不同，原本设定好的相位就会有所变化，例如原来固定在0°的载波可能会在过零点的左侧，即滞后，或右侧，即超前，这就需要将这个误差相位平均分配到20个载波中，通过修改它们的周期使得下一个工频周期时，将载波的相位固定在0°位置处。

(1)移相角为0°

如图 2所示，判断实际载波处于上升区或下降区的标志位，如果处于下降区，则在1的位置处，载波滞后于理想状态，在之后的20个载波中，周期要相应的缩短；如果处于上升区，则在2的位置处，载波超前于理想状态，在之后的20个载波中，周期要相应的延长。

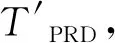
(9)

式中：TERROR为实际载波与参考载波在网压过零点时刻之间的误差。

图3 基于周期控制的载波移相角校正方法(移相角为0°)

(2)移相角非0°

实际载波处于上升区的位置：如图 2所示，判断当前实际载波计数值与理想计数值差值的正负，如果是正的，则处于2的位置，载波超前于理想状态，在之后的20个载波中，周期要相应的延长；如果是负的，则在1的位置处，载波滞后于理想状态，在之后的20的载波中，周期要相应的缩短。

实际载波处于下降区的位置：这种情况说明载波的实际位置与理想位置偏差较大，以图 2中的90°为例，若载波在下降区内，则处于3或4的位置，载波滞后或超前于理想状态，在之后的20个载波中，周期要相应的缩短或延长。而载波究竟是处于3的位置还是4的位置，需要进一步判定。

在此，利用的是EPWM模块里的中断功能，在程序设定中，EPWM1是作为第一个桥臂开关管的控制量，其频率为开关管频率，EPWM6用来产生中断，并且其频率与开关管频率相同(均为1 kHz)，这样就可以利用EPWM6产生的中断来为EPWM1的载波进行编号，载波编号依次为1，2，…，19，0，1，2，…。以90°为例，如图 4所示，若在相位同步时检测到载波计数处于下降区，且编号为1，说明实际载波超前于参考载波，需要增大载波的周期，此时实际载波的位置相当于在图 2的4位置处。相应的计算公式为

(10)

若相位同步时检测到载波编号为0，说明实际载波滞后于参考载波，需要减小载波的周期，此时实际载波的位置相当于图2的3位置处。

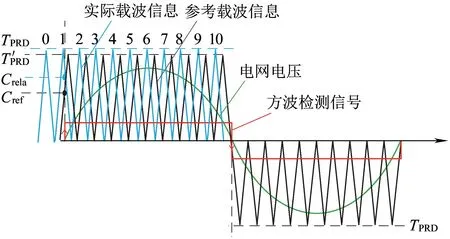
图4 基于周期控制的载波移相角校正方法(移相角非0°)

基于周期控制的移相角校正方法可用表 1表示，该方法同样适用于N个四象限变流模块。

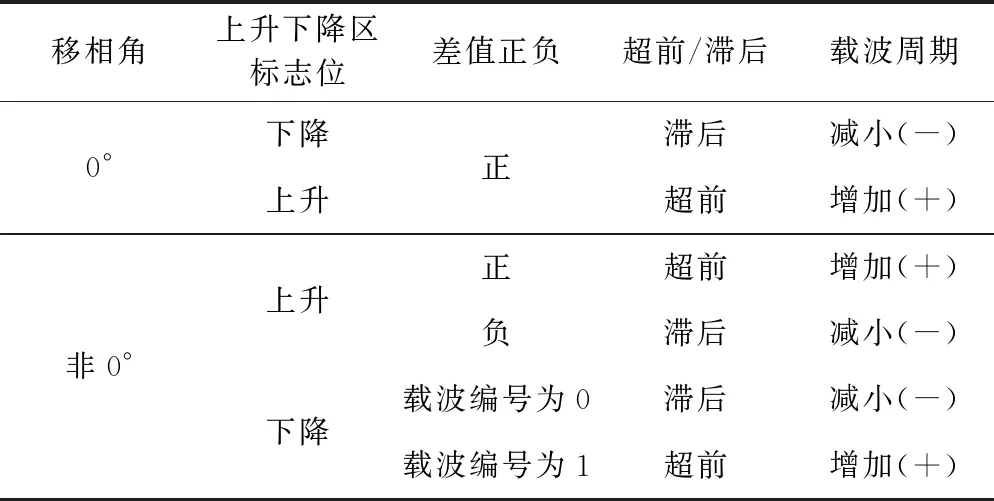
表1 周期控制的移相角校正策略

3 仿真与实验验证

为了对本文提出的基于周期控制的载波移相策略进行验证，搭建了单相四象限变流器的仿真模型及实验平台，相关仿真及实验参数见表 2[14]。仿真与实验是针对两台变流器，即4个四象限变流模块进行的。

表2 仿真及实验参数

3.1 仿真验证

仿真主要验证本文提出的基于周期控制的载波移相策略对于抑制开关次谐波的有效性。

仿真模拟两台变流器，4个四象限变流模块额定功率运行情况，4个载波的移相角分别为0°、90°、45°、135°。采用本文提出的基于周期控制的载波移相策略，900 V侧交流电流Is1～Is4放大波形如图5所示。若不采用载波移相策略，四路电流波形的小锯齿应完全重合[15]，而从图5可以看出Is1～Is4波形在载波移相控制下形成锯齿波，说明这4个模块的载波彼此之间存在相位差，从而实现移相控制。

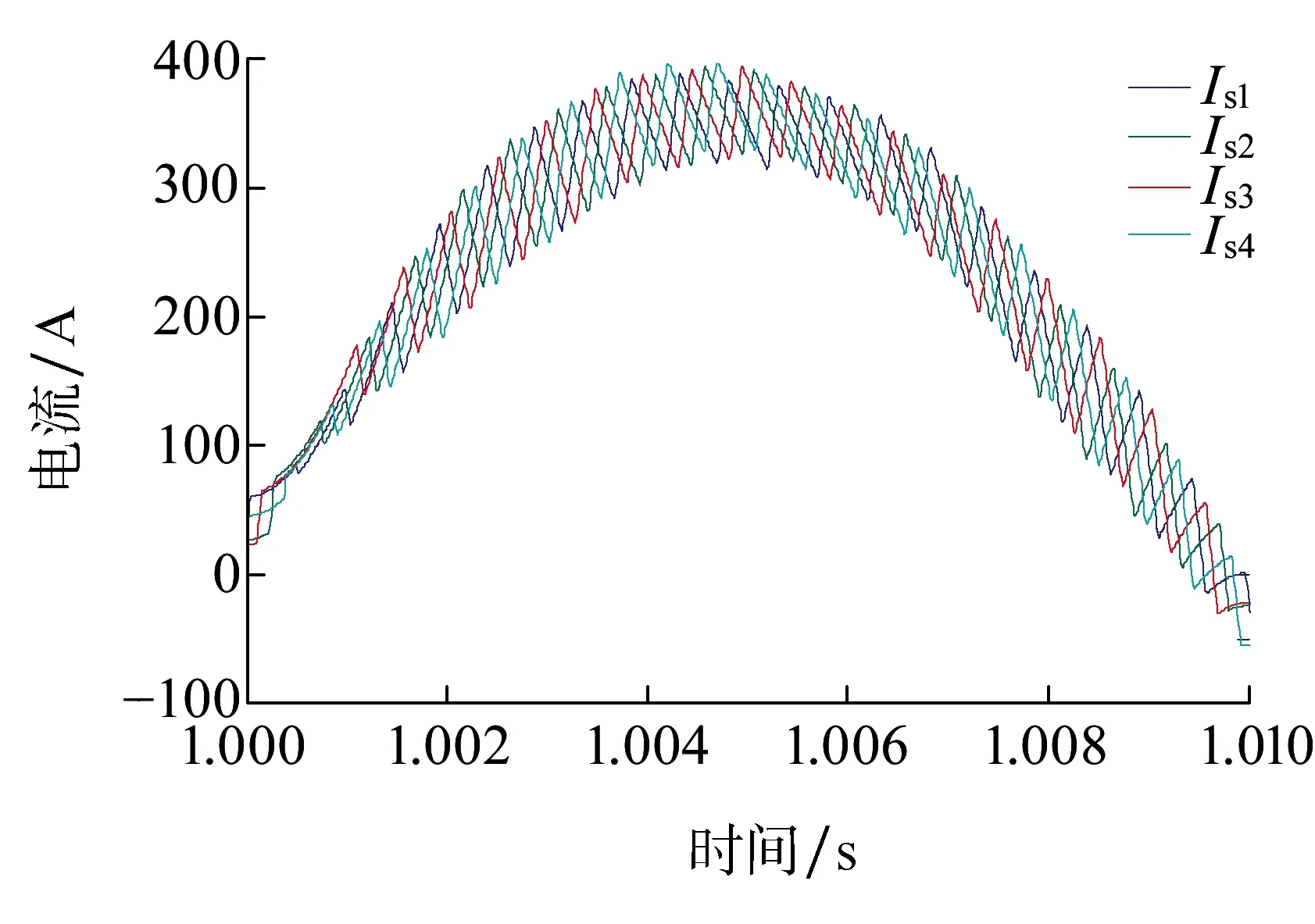
图5 载波移相控制下的900 V侧四路交流电流Is1～Is4波形

对四象限变流器采用本文提出的载波移相策略前后进行对比，说明该策略的有效性。图6为采用该策略时，牵引变压器一次侧交流电流的THD，其值仅为1.05%。

图6 采用载波移相策略的牵引变压器一次侧交流电流THD(基波(50 Hz)=51.93 A,THD=1.05%)

当不采用载波移相策略时，牵引变压器一次侧的交流电流THD如图7所示，其值高达9.09%。

图7 不采用载波移相策略的牵引变压器一次侧交流电流THD(基波(50 Hz)=51.64 A,THD=9.09%)

从仿真结果可以看出，采用本文提出的载波移相策略可以大幅度降低开关次频率谐波，从而将电流总THD降到很低。

3.2 实验验证

实验验证主要分为三部分：通过测量不同变流器内主控板中的两个载波，说明载波之间相位不能长期保持定值的问题，得出载波相位需要在四象限变流器运行过程中适当调整，从而保持载波相位之间的相对固定；用实验证明采用四象限变流器运行中强制给相位寄存器赋值的方法来校正相位，会引起交流电流不稳定；采用本文提出的基于周期控制的载波移相策略，并用实验证明其有效性。

(1)不同变流器内主控板之间载波相位不固定

两块主控板产生的开关脉冲分别为A和B，开关脉冲波形的相位可以反映出两块板子内部的载波相位情况，其初始相位如图8所示。基准线1位于A的第一个脉冲尾端(第二个脉冲首端)，基准线2与B的第二个脉冲的交点为M。

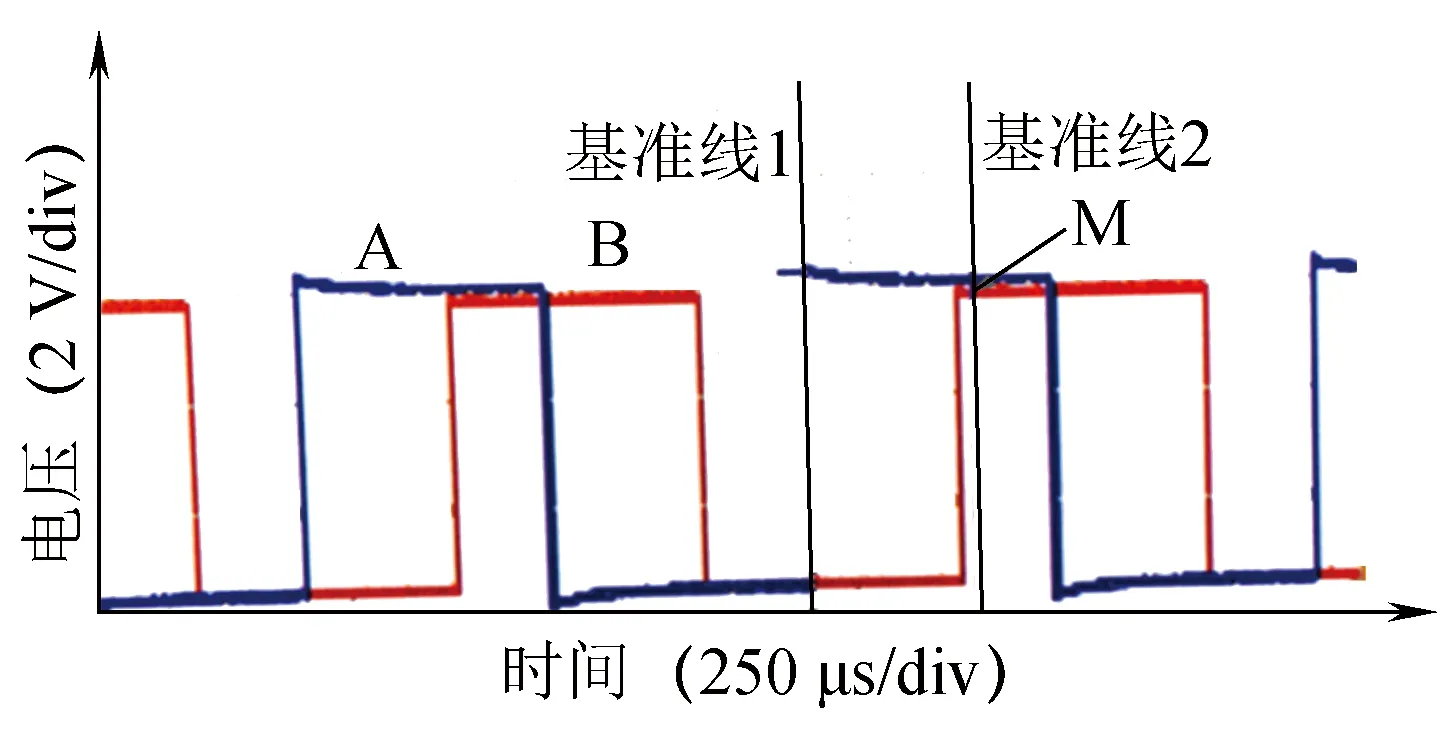
图8 开关脉冲初始相位

经过7 min后，开关脉冲B移动了180°，其波形如图9所示。

图9 7min后开关脉冲相位

由此可见，如果在四象限变流器运行的过程中不修正载波相位，载波之间的移相角就是不固定的，由此很难实现载波移相减小开关频率谐波的目的，所以必须在四象限变流器运行过程中实时校正相位。

(2)四象限变流器运行过程中强制给载波相位寄存器赋值

若采用在四象限变流器运行过程中强制给载波相位寄存器赋值的方法来实时校正相位，则会使交流电流难以保持稳定状态，两个四象限变流模块空载运行，其交流电流Is1和Is2如图10所示。因为由前面的实验可以证明，不同主控板之间的载波相位不固定，若强制校正载波的相位将导致形成的开关脉冲不完整，从而使交流电流不稳定，因此这种方法也不能采用。

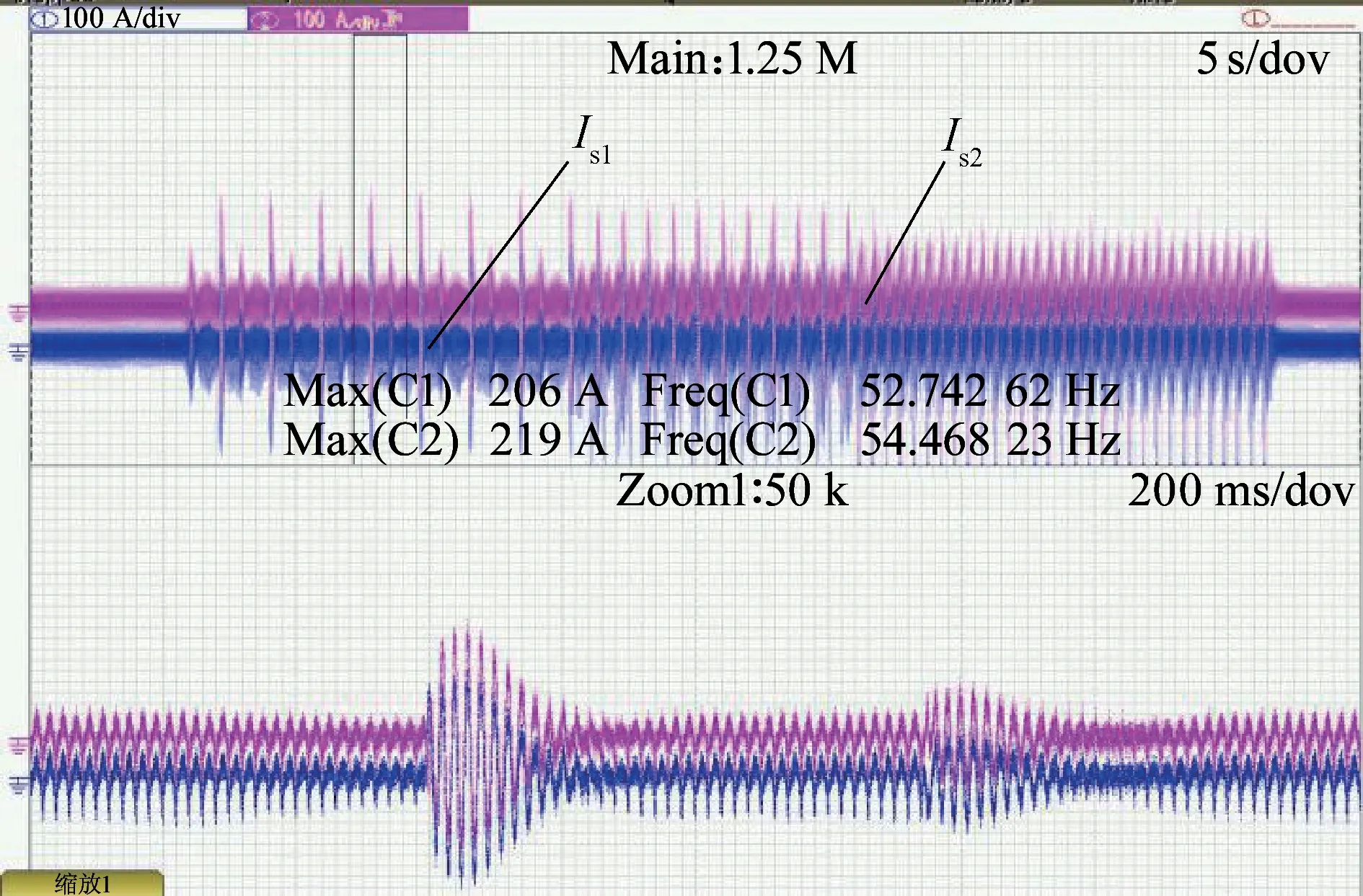
图10 强制给寄存器赋值的载波移相策略空载运行时交流电流Is1和Is2波形

(3)基于周期控制的载波移相策略

采用基于周期控制的载波移相策略对载波的相位调节相对缓慢，对开关脉冲的影响较小，因此可以满足交流电流稳定的要求，同时固定了移相角度，通过谐波对消达到减小开关次频率谐波的作用。两个四象限变流模块空载运行，其交流电流如图11所示。

图11 基于周期控制的载波移相策略空载运行时交流电流Is1和Is2波形

当四象限变流器运行于带载状态时，也能够保持稳定，并且谐波含量较小，完全符合要求。我国完全自主研发的混合动力动车组就是采用这种基于周期控制的载波移相策略。图12为现场测试图。

图12 混合动力动车组谐波测试

该混合动力动车组牵引变压器一次侧额定电流为51.2 A，由于车上的电流互感器为250∶1，副边可测得的交流电流仅有0.204 8 A，无法直接测量其THD，而互感器原边由于结构上的原因不方便测量，所以在互感器副边的导线中串联一个150匝的线圈，将电流放大，从而方便测量。此时，额定工况下，电流互感器副边可测得的电流值为30.72 A。

当机车运行于额定功率时，若只在四象限变流器发脉冲前设定载波移相角，而不采用基于周期控制的载波移相策略，测得的谐波含量分布如图13所示。若采用该策略，测得的谐波含量分布如图14所示。

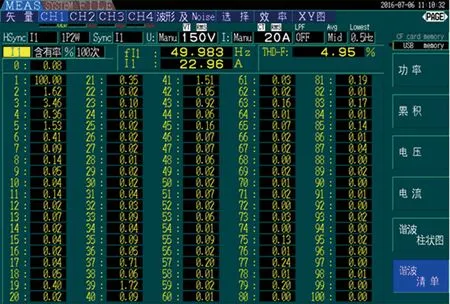
图13 不采用载波移相策略牵引变压器一次侧电流THD

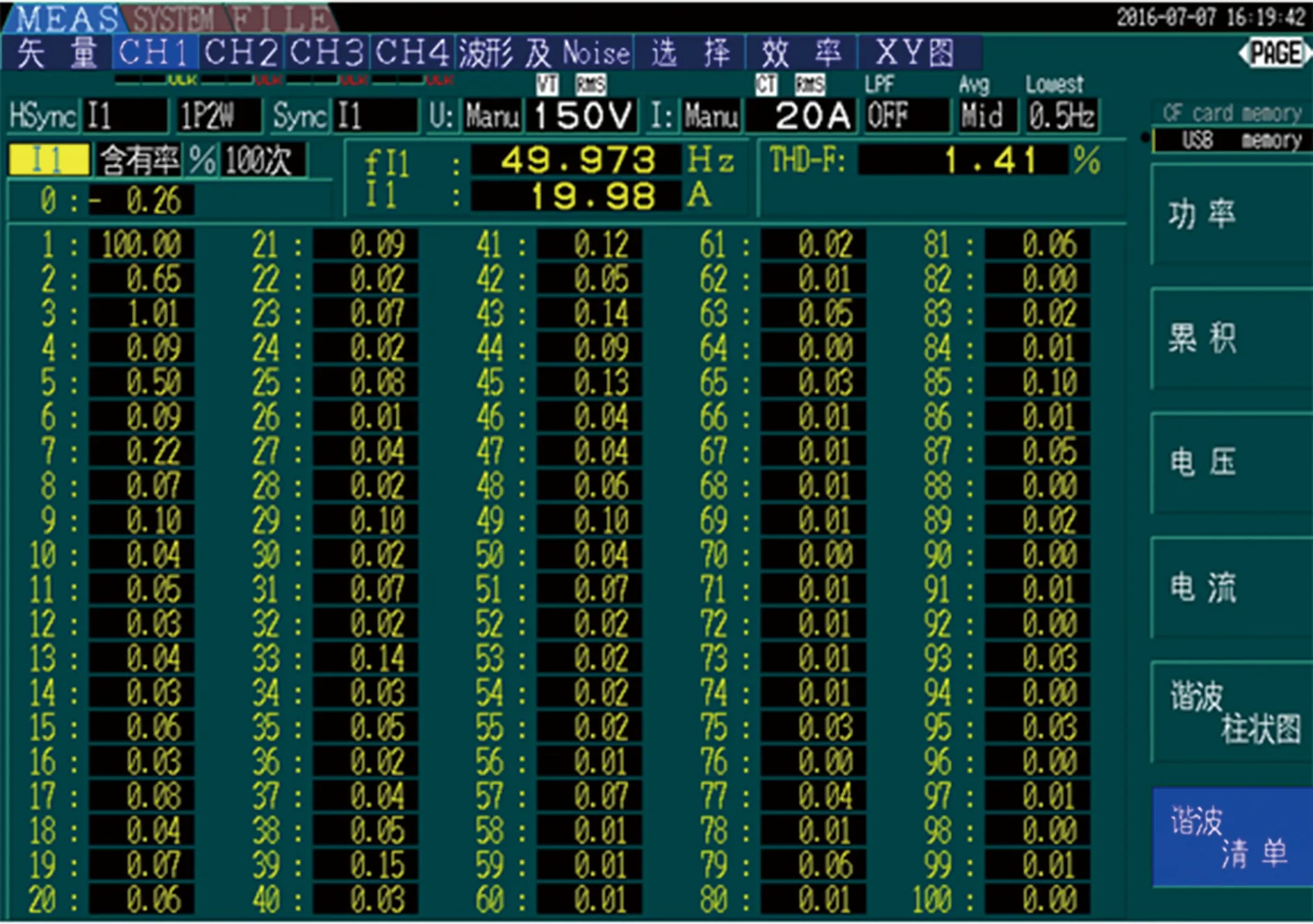
图14 采用载波移相策略牵引变压器一次侧电流THD

对比图13和图14可知，当不采用基于周期控制的载波移相策略时，虽然在四象限变流器发脉冲前设定了载波移相角，但其开关次谐波含量依旧较高，如37、39、41和43次(采用单极性倍频调制，因此特征次谐波为开关频率的两倍)，从而总THD较高，不满足额定工况下THD<2.5%的要求；若采用基于周期控制的载波移相策略，37～43次的奇数次谐波含量较低，并且总THD仅有1.41%，完全符合要求，从而证明了该载波移相策略的可行性和有效性。

4 结论

(1)介绍一种基于周期控制的载波移相策略及实现方法，并通过理论计算，分析了基于载波移相的谐波对消原理，进而介绍了载波移相策略的具体实现方法。该方法在同一列车多个牵引系统之间无同步线的情况下，以网压过零点为参考点，通过微调PWM载波周期，固定载波移相角，实现载波移相的功能，并且在列车运行过程中能够保持系统稳定。

(2)通过仿真及混合动力动车组运行实验，验证了基于周期控制的载波移相策略在减小开关次谐波方面的有效性，以及该策略能够满足系统运行稳定性的要求，从而为工程实践提供指导。