考虑徐变效应的高速铁路预应力箱梁上拱变形时变可靠度研究
2019-08-01卢朝辉余志武
邹 红,卢朝辉,余志武
(中南大学土木工程学院,湖南长沙 410075)
我国高速铁路双线预应力混凝土桥梁大量采用简支箱梁结构。梁体变形会改变桥上轨道结构的几何形状甚至影响轨道平顺性和行车安全,因此,预应力混凝土梁的后期上拱变形是桥梁服役性能演化中需要关注的重要内容之一[1]。与有砟轨道可以通过道砟调节轨道高程不同,无砟轨道只能通过扣件调节使轨道恢复其正常的几何形状,但扣件的可调量又比较有限,因此文献[2]对高速铁路预应力箱梁上拱变形提出了限值。
国内外学者对预应力箱梁徐变上拱做了大量研究。文献[3]采用徐变系数B3模型,结合混凝土材料的时变特性,对高速公路不同跨径预应力简支箱梁跨中上拱度提出预测模型。文献[4]基于国内外现有设计规范的徐变系数模型,采用数值分析方法对大跨度预应力混凝土桥梁不同截面以及不同时刻的上拱变形进行计算,同时,文中混凝土梁足尺试验研究表明:适当延后预应力张拉和铺轨时间可有效控制无砟轨道预应力混凝土梁的后期徐变变形。文献[5]提出了上拱徐变控制措施。文献[6]以HSC(C50)和HPC(C50)试验梁为研究对象,分析梁体上下缘应力差、钢筋配筋率及环境等因素对收缩徐变及上拱变化的影响。
上述研究均为徐变系数模式中参数为确定性变量条件下所开展的预应力混凝土梁上拱度分析,忽略了徐变系数模型中诸如环境湿度、混凝土强度等参数不确定性的影响。文献[7]将混凝土强度、水灰比、环境湿度等参数视为随机变量,基于蒙特卡洛方法,开展试验梁上拱时变可靠度研究。文献[8]将徐变计算模型中的加载龄期、构件理论厚度、混凝土弹性模量等参数视为随机变量,利用大型通用软件ANSYS中的PDS模块对某公路桥跨中上拱时变可靠度进行研究。
但是,基于蒙特卡洛方法的可靠度计算较为耗时,国内外针对服役中高速铁路预应力简支箱梁上拱可靠性分析的研究则鲜有报道。因此,选择一种计算相对简便、计算结果精度又能满足要求的高速铁路箱梁上拱变形可靠度计算方法显得尤为重要。
本文基于PSC箱梁分别在一期恒载、二期恒载与有效预应力作用下的上拱变形计算式,建立考虑徐变效应的预应力混凝土(PSC)箱梁跨中截面上拱变形功能函数,利用该函数开展基于矩法的某客运专线32 m PSC箱梁跨中上拱变形时变可靠度研究:利用基于二维减维积分的7点估计方法计算不同服役时刻t的功能函数的前三阶矩;采用三阶矩可靠度公式求出任意时刻t的可靠度指标及相应失效概率。
1 考虑徐变效应的箱梁上拱变形时变功能函数的建立
文献[6]认为:梁体截面上下缘应力差越大则此截面后期上拱度越大,根据高速铁路箱梁预应力筋布置特点,本文选取上下缘应力水平差最大的跨中截面为研究对象。考虑到梁体混凝土材料的时变特性和不同施工阶段的受力特点,将跨中截面上拱时变可靠度极限状态函数(功能函数)表示为
G(t)=[Δ]-f(t)
(1)
式中:[Δ]为桥梁上拱变形限值;f(t)为箱梁不同服役时刻t外界荷载使梁体跨中产生的上拱变形总和。由于考虑徐变效应的梁体上拱变形仅与恒载有关,因此,本文针对梁体变形的讨论仅限于恒载作用的上拱变形[9]fg(包括一期恒载挠曲变形fg1、二期恒载挠曲变形fg2)和预应力张拉产生的上拱变形fp。
1.1 考虑徐变效应的梁体自重挠曲变形
对于无砟轨道PSC箱梁,一期恒载指梁体自重;二期恒载包括钢轨、扣件、轨道板、砂浆层、底座板等永久荷载。
将一期恒载和二期恒载视为集度分别为q1和q2的均布荷载,则产生的跨中挠曲变形为[9]
fg=fg1[1+φ(t,τ1)]+fg2[1+φ(t,τ2)]
(2)
式中:τ1为一期恒载加载时间;τ2为二期恒载加载时间;φ(t,τ1)和φ(t,τ2)分别为加载龄期τ1和τ2至计算龄期t(t≥τ2≥τ1)的徐变系数;fg1和fg1分别为一期恒载和二期恒载作用下简支梁的挠度
(3)
式中:E为混凝土弹性模量;I为PSC箱梁截面惯性矩;l为计算跨径。
1.2 考虑徐变效应的预应力张拉上拱变形
考虑到预应力损失的影响,计算张拉力产生的挠度时,计算荷载取控制张拉应力与最终有效预应力的平均值[9]
(4)
式中:fpe和fpi分别为初张拉力Npe和终张拉力Npi作用引起的瞬时弹性上拱变形值;式中的负号表示梁体上拱,与自重作用下的挠曲变形方向相反;τ0为预应力筋终张拉时间(t≥τ0)。
文献[10]认为:初张拉力Npe和终张拉力Npi引起的上拱变形fpe和fpi为
(5)
式中:ep为预应力筋合力点到截面重心的距离。
将式(2)~式(5)代入式(1),可得到高速铁路PSC箱梁跨中截面上拱时变可靠度极限状态函数

(6)
1.3 徐变系数计算模型的选取
目前,国内外研究人员进行混凝土结构上拱变形分析时所采用的徐变系数计算模型并不统一。文献[3]通过将文献[11]与文献[12]徐变系数模型进行对比分析,选取B3模型对高速公路桥梁结构后期上拱变形开展研究。文献[13]以C60预应力混凝土梁试件为研究对象,基于实验室标准徐变试验得到的徐变系数实测数据,对文献[14-15]常用的徐变系数模型进行对比分析研究。本文将上述文献所采用的徐变系数计算模型预测值与文献[13]的徐变试验数据进行对比,如图1所示。
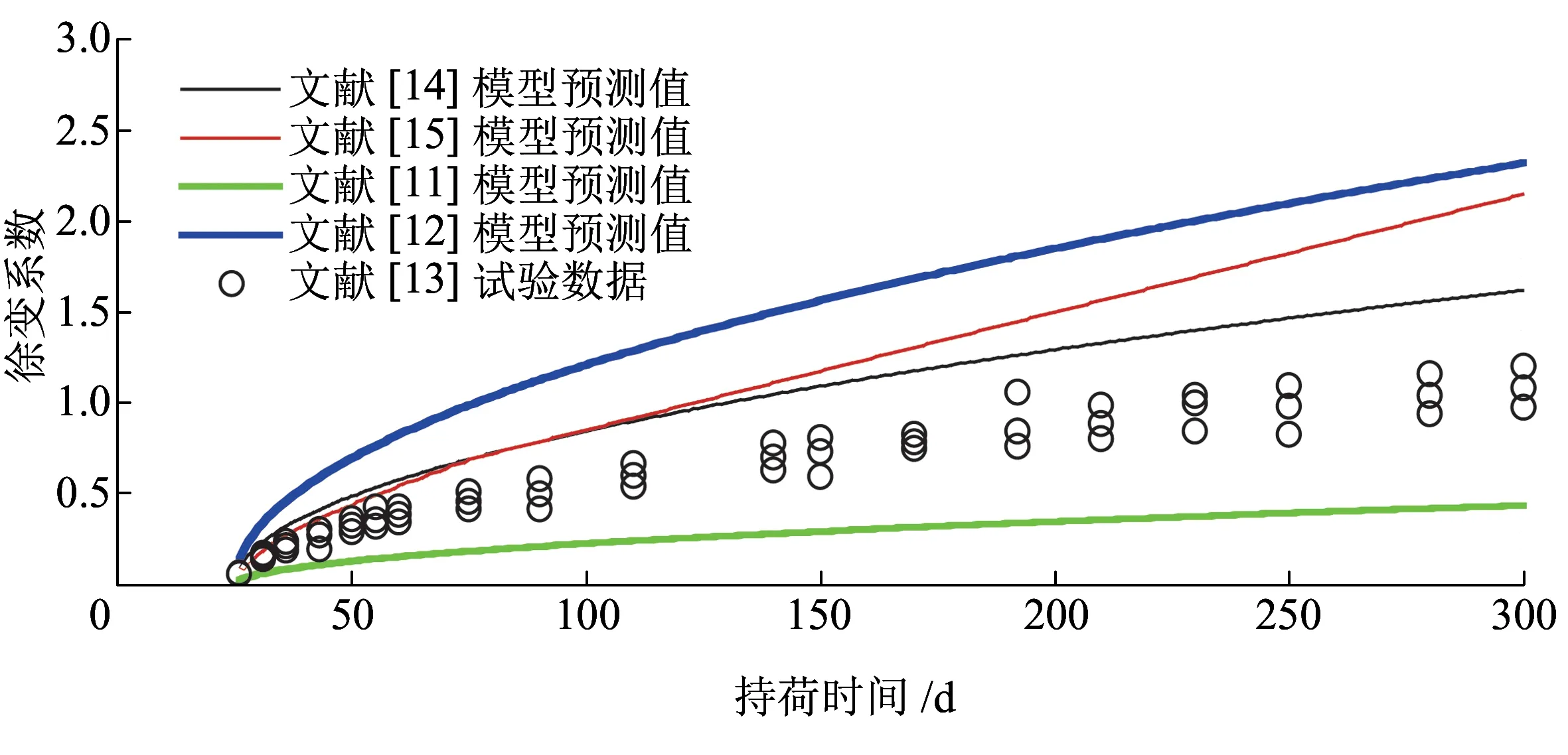
图1 徐变系数计算模型预测值与徐变试验数据对比分析
从图1可以看出:对比分析所采用的4个徐变系数模型的预测值均与实测值出现了不同程度的偏差,其中文献[12]模型的预测值远大于试验值,而文献[11]模型的预测值远小于实测值,与实测值误差最小的是文献[14]模型的预测值。文献[16]采用不同徐变系数模型对在役铁路预应力混凝土桥梁的上拱变形进行分析计算,并与实测值进行对比研究,得到了类似的结论。因此,本文拟选取文献[14]中的徐变系数模型,该模型计算表达式为

(7)
式中:RH为环境年平均相对湿度;RH0=100%;h为构件理论厚度,h=2A/u,A为构件面积,u为与大气接触的周边长度;h0=100 mm;fcm为28 d龄期混凝土立方体抗压强度平均值;fcm0=10 MPa;t和τ分别为混凝土计算龄期和混凝土加载龄期,t≥τ;(t-τ)为持荷时间;t1=1 d。
2 梁体上拱变形可靠度分析的三阶矩方法
2.1 点估计方法计算功能函数前三阶矩的基本思想
根据文献[17],功能函数G(X)的k阶原点矩可以表示为
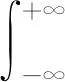
(8)
式中:fX(x)为随机向量X的联合概率密度函数;T-1(u)为逆正态转换;φ(u)为标准正态随机向量的联合概率密度函数。
令L(u)={G[T-1(u)]},采用二维减维积分方法,L(u)可以表示为[18]
(9)
L0=L(0,…,0,…,0)
(10)
(11)
(12)
式中:L1为n个一维函数总和;L2为[n(n-1)]/2个二维函数的总和;ui、uj分别为标准正态空间中的随机变量。
将式(9)~式(12)代入式(8),可得
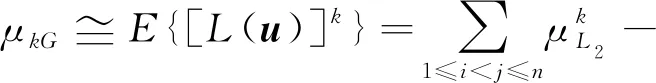
(13)
其中
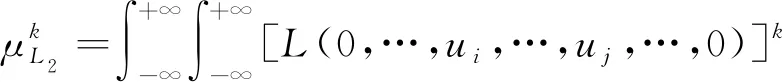
(14)
(15)
(16)
利用Gauss-Hermite积分公式,一维函数积分式(15)可近似表示为
(17)
式中:uir为标准正态分布空间中第i个变量的第r个估计点(高斯估计点);Pr为与uir对应的权重值;m为估计点数。若采用标准正态分布空间中的7点估计,其估计点值uir及权重Pr为
(18)
同理,二维函数积分式(14)可以近似表示为
(19)
式(9)~式(19)均为基于标准正态空间的计算式,由于功能函数一般表示为原始空间随机变量的函数,基于逆正态变换,式(10)~式(12)、式(16)可分别转化为原始空间的计算式。
L0=Gμ(μ1,…,μi,…,μn)
(20)
(21)
(22)
(23)
式中:Gi(μ1,…,xi,…,μn)为将G(X)中参数xi视为随机变量、其余变量取对应分布均值时的一维函数;Gi,j(μ1,…,xi,…,xj,…,μn)为将G(X)中参数xi、xj视为随机变量而其余变量取对应分布均值时的二维函数。将式(20)~式(23)分别代入式(17)和式(19),可得
(24)

(25)
式中:T-1(uir)、T-1(uir1)和T-1(ujr2)分别为标准正态空间高斯估计点uir、uir1和ujr2通过逆正态变换得到的对应原始状态空间的值;Pr、Pr1和Pr2为相应的权重。
利用式(23)~式(25)和式(13),可计算得到功能函数G(X)的前三阶原点矩,即μ1G、μ2G和μ3G。根据原点矩和中心矩的定义,可得到功能函数G(X)的前三阶中心矩为
μG=μ1G
(26)
(27)
(28)
式中:μG、σG和α3G分别为功能函数G(X)的均值、标准差和偏度。
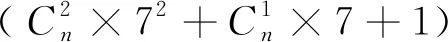
2.2 梁体上拱变形时变功能函数前三阶矩的计算
对于式(6)所示考虑徐变效应的箱梁上拱变形时变功能函数,式(24)、式(25)和式(23)可表示为
(29)

(30)
(31)
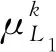
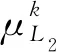
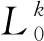
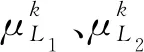
2.3 三阶矩可靠度指标及失效概率计算
得到功能函数的前三阶中心矩后,根据文献[19],可通过采用三阶矩可靠度指标和相应失效概率计算公式进行结构可靠度计算分析。
(32)
(33)
式中:β3M为三阶矩可靠度指标;Pf为失效概率;Φ(·)为标准正态随机变量的累积分布函数。
3 算例
某客运专线桥梁采用单箱单室箱形预应力混凝土简支梁,设计使用寿命为100年,桥面上铺设CRTSⅡ型板式无砟轨道板,跨中、梁端结构尺寸及预应力配筋情况如图2所示[20]。该梁的计算跨度l为31.5 m,梁惯性矩I为9.1 m4,预应力偏心距ep为1.458 m,理论厚度h为406 mm;梁体采用现浇C50混凝土;预应力钢绞线为1×7-15.2-1860[21],预应力筋数量见表1;锚具体系采用自锚式拉杆体系。梁体施工中预应力钢绞线张拉采用应力、应变双重控制,预应力束的控制应力初张拉时为0.56fptk,终张拉时为0.725fptk,fptk为φ15.2钢丝抗拉强度标准值。环境类别与作用等级:一般大气条件下无防护措施的地面结构,环境类别为碳化环境,作用等级为T2。终张拉时间为τ0=14 d,落梁时间为τ1=30 d,铺轨运营时间为τ2=270 d[9]。
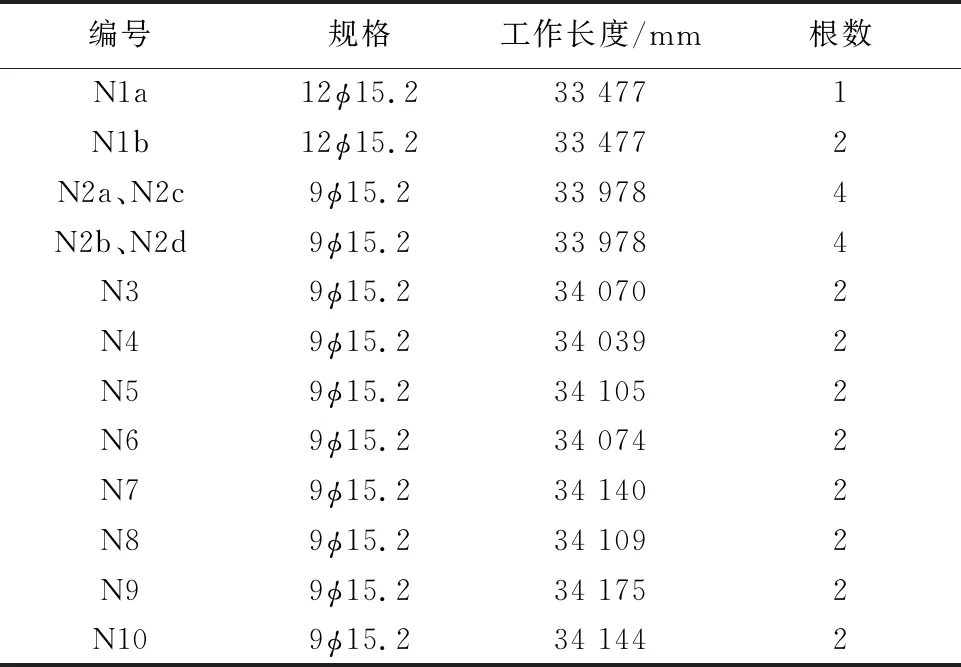
表1 预应力筋数量
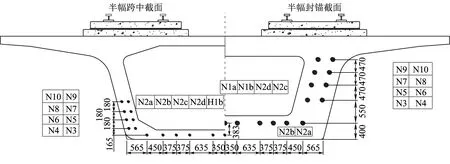
图2 箱梁横断面(单位:mm)
3.1 随机变量及其7点逆正态转换值
本文用到的随机变量见表2。初张拉预应力Npe及终张拉预应力Npi均视为随机变量,本文按照PSC箱梁预应力筋初张拉与终张拉的钢束数目,均值分别拟定为11.728×103kN、36.060×103kN,根据文献[22]研究成果,变异系数均取为0.04,且服从正态分布。文献[23]对桥梁的长期监测数据表明:环境相对湿度服从均值为67.3%、变异系数为0.19的正态分布。为了得到不同标号混凝土的弹性模量与轴心抗压强度的历时变化模型,文献[24]对不同龄期和不同设计强度混凝土的早期轴心抗压强度和弹性模量等概率分布开展大量试验研究,数据结果统计表明C50混凝土早龄期轴心抗压强度和弹性模量随机过程的概率分布模型均不拒绝对数正态分布,其中弹性模量服从均值为32.13 MPa、变异系数为0.192的对数正态分布,轴心抗压强度服从均值为44.93 MPa、变异系数为0.221的对数正态分布。文献[25]对高速铁路箱梁结构的承载力进行可靠性分析时,分别假定一期恒载与二期恒载服从均值为218.3 kN/m和128.4 kN/m、变异系数为0.021 4和0.068 1的正态分布。

表2 随机变量分布类型
根据表2随机变量的分布特征,基于式(18)采用逆正态变换求出相应原始空间估计值,见表3。
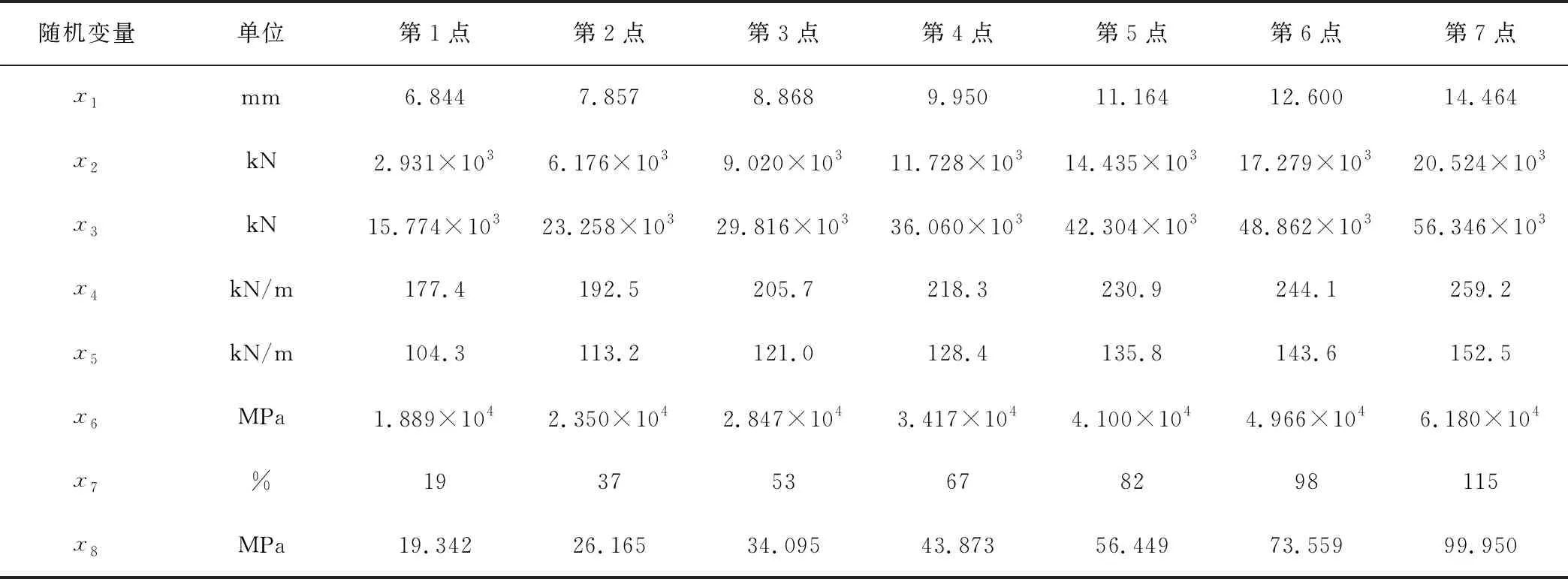
表3 高斯点对应的各随机变量原始空间值
3.2 PSC箱梁跨中上拱变形时变可靠度计算

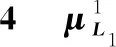
表计算结果 mm
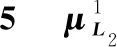
表计算结果 (i 表6 功能函数前三阶矩及可靠度指标 (t=τ0=14 d) 采用50万次蒙特卡洛模拟所得的可靠度指标也示于表6中。通过表6对比分析可知,本文方法大幅缩减了计算次数,同时与蒙特卡洛可靠度指标只相差0.001,满足精度要求。 同理,当t∈(τ0,t]时,重复上述计算过程,可以得到PSC箱梁跨中上拱变形的时变可靠度,计算结果如图3所示。 图3表明:箱梁跨中截面上拱变形时变可靠度变化区间为[1.217,2.665];当预应力张拉完毕后,瞬间会有一个弹性上拱,并且此时由于徐变系数的发展,在预应力条件下,上拱变形会继续增加,因此在一期恒载加载(落梁)前,其上拱变形可靠度呈现下降趋势;落梁后,梁体自身重力产生的挠曲向下,与上拱方向相反,此时上拱变形可靠度会出现如图3所示的向上的突变点;类似地,二期恒载加载(铺轨)之后再次产生了向上的突变点;随后由于徐变系数的发展变形趋于平稳,上拱变形可靠度也缓慢增长,最终梁体甚至可能出现整体向下挠曲的状态。 图3 PSC箱梁跨中上拱变形时变可靠度 另外,从PSC箱梁跨中上拱变形极限状态函数式(6)可以得知:若减小预应力筋合力点至截面重心轴的距离(ep),将降低梁体跨中截面上下缘应力水平差,从而能够改善箱梁跨中截面徐变上拱变形可靠度水平,这与文献[6]基于确定性参数条件下的上拱变形分析得到的结论类似。目前,高速铁路箱梁采用全预应力结构进行设计,工程设计人员采用了较高的有效预应力设计值,以达到梁体结构不开裂的目的,通过式(6)可知有效预应力越大,上拱变形可靠度越低,这也是易造成上拱变形可靠度整体水平较低的原因之一。 上拱超限会严重影响列车竖向加速度以及斯佩林指数[7],而目前我国相关设计规范并未明确规定上拱变形的最低可靠度水平,为了最大程度地满足高速列车运行的平稳与舒适性要求,建议工程设计人员采取降低预应力偏心距等措施来进一步提高箱梁上拱可靠度。 (1)本文建立了考虑徐变效应的PSC箱梁跨中截面上拱变形极限状态函数,利用此极限状态函数,发展了基于三阶矩法的箱梁跨中上拱变形时变可靠度分析方法:采用基于二维减维积分的7点估计方法计算极限状态函数的前三阶中心矩(均值、方差、偏度),并采用三阶矩可靠度公式计算其可靠度指标及失效概率。 (2)多种徐变系数模型计算结果与实测结果比较分析表明:《JTG 3362—2008 公路钢筋混凝土及预应力混凝土桥涵设计规范》中的徐变系数模型与实测结果最吻合,计算结果更符合实际工程。 (3)与蒙特卡洛方法的对比分析表明:本文求解可靠度的方法能够大幅减少计算次数,同时也能够保证计算结果的精度,可方便应用于高速铁路桥梁结构徐变上拱变形时变可靠度分析。 (4)时变可靠度分析结果表明:预应力张拉之后上拱可靠度呈现出下降趋势;一期恒载与二期恒载加载后上拱变形可靠度一直处于上升阶段,由于后期徐变系数发展得更缓慢,因此二期恒载加载后可靠度上升趋势更平缓。由于目前我国设计规范对上拱变形可靠度最低水平未做明确规定,同时为了最大程度地满足列车运行平稳与舒适性要求,建议工程设计人员采取降低预应力偏心距等措施,来整体提高PSC箱梁跨中上拱变形可靠度值。 本文未考虑高频列车荷载反复作用对徐变上拱变形的影响,因此计算结果存在一定的局限性,有待今后进一步深化研究和改进。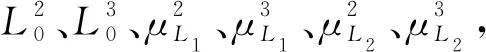


4 结论
