Remaining Useful Life Prediction of Rolling Element Bearings Based on Different Degradation Stages and Particle Filter

LI Qing，MA Bo，LIU Jiameng

Beijing Key Laboratory of High-End Mechanical Equipment Health Monitoring and Self-recovery，Beijing University of Chemical Technology，Beijing 100029，P.R.China

Abstract: A method is proposed to improve the accuracy of remaining useful life prediction for rolling element bearings，based on a state space model（SSM）with different degradation stages and a particle filter. The model is improved by a method based on the Paris formula and the Foreman formula allowing the establishment of different degradation stages. The remaining useful life of rolling element bearings can be predicted by the adjusted model with inputs of physical data and operating status information. The late operating trend is predicted by the use of the particle filter algorithm. The rolling bearing full life experimental data validate the proposed method. Further，the prediction result is compared with the single SSM and the Gamma model，and the results indicate that the predicted accuracy of the proposed method is higher with better practicability.

Key words: different life stages of state space model; remaining useful life prediction of rolling element bearing;particle filter

0 Introduction

Rolling element bearings are widely used as components of rotating machinery， determining working fluency of the equipment. Equipment maintenance should be conducted at an appropriate period to avoid instrument breakdown or damage that may result from improper shut down，However，determination of when this maintenance should be performed requires accurate analysis.

The remaining useful life of rolling element bearings can be determined using the statistic- based model method， the mechanics-of-fracture-based model method，and the data-drive-based model method[1-7].The remaining useful life of rolling element bearings is analyzed by the bearing failure mechanism coupled with mathematical statistics in the statistics-based approach. A reliability-based formula is established using observation data and failure mechanism to allow the description of parameters.In addition，Kalman filter has been applied to the research of remaining useful life[8]. Although the discrete result and the fixed model cannot be adjusted，they are widely used in real applications.

The model of crack growth was established to forecast the remaining useful life of rolling bearings with the assumption that the failure process is the same as the mechanics of crack growth described in the fracture-based model method. Significant expert experience and complex knowledge of fault mechanisms are needed for that method，and this approach is not suitable for monitoring working equipment in actual time with changeable parameters.

The remaining useful life of rolling element bearings can be analyzed using the status information in the data-drive-based model method. The physical complexity and the uncertainty can be resolved using this method，and online adjustment can be performed in the real process in consideration of the status of rolling elements. However，the attenuation pattern is not clear and there can be significant effects of individual parameters due to the neglect of basic principles in this method. Grenerally，developments of an online approach to accurately predict the remaining useful life of rolling element bearings with a lower requirement for observed process status and the trend of change which makes this prediction in a timely fashion remain a significant challenge in this field.

The failure crack growth curve of rolling element bearings is composed of three sages[9]. The first stage is the change from emergence to growth of the crack. The second stage is the stable growth of the crack，also referred to as the Paris Region.The third stage is the process of instability and fast fracture of the crack. The simple physical model of rolling bearings is used to predict the remaining useful life by describing the second degradation stage，and the accuracy is limited by incomplete degradation description.

In this paper，a method of state space model（SSM）and particle filter（PF）for life prediction of rolling element bearings based on a different degradation stage is proposed. In this method，the Paris formula[10]and Foreman formula[11]are adjusted to model the degradation stages. The model is then adjusted with the process status of the rolling element bearing to fit the degradation trend. The real working status of the rolling bearing is predicted by the improved model and the particle filter algorithm to analyze the remaining useful life.

1 Theory of Life Prediction Method

1.1 State space model

SSM is a dynamic time-domain model with implicit time as the independent variable. SSM contains two models. The first is a state equation model，which reflects the transferred state of a dynamic system influenced by input variables at a certain moment. The second is an output or measurement equation model，which links the output of the system at a certain moment to the state and input variables of the system.

The SSM is usually defined as follows

SSM incorporates non observable variables（state variables）into an observable model，and uses the model to determine the estimated result. At the same time，SSM can describe the state of the system by using the minimal present or past information，which does not require a large amount of historical data，minimizing the time and effort of the operation process.

1.2 Particle filter algorithm

The PF algorithm describes the dynamic model of the system by using the state equations and describes the observation model of the system based on observation equation. This approach can deal with a time-varying system，non-stationary signal，and multidimensional signal. The application of the PF algorithm largely solves the difficult calculations required for use of the state-space method. The PF algorithm is based on Bayesian estimation and Monte Carlo methods，using particle collection to denote the probability. The PF algorithm can be used in any SSM in multiple forms. The core principle is expression of the distribution by using a random state particle extracted from the posterior probability. In brief，PF approximates the probability density function by looking for a set of random samples in the state space，then replaces integral calculation by using the sample mean to obtain the state minimum variance estimation.

The PF algorithm includes particle generation，importance sampling，weight update，resampling，state estimation，and other steps[13]. The specific steps used in this implementation are as follows：

（1）Particle set initialization，k=0

For i=1，2，… ，N，The sampling particlesare generated by the prior probability distribution p(xo)，w(i)o=1/N.

（2）Importance sampling

For i=1，2，…，N，sample

and set

（3）Updating importance weights

Calculate the particle importance weight

and normalized weight

（4）Resampling

Calculate number of valid samples

If Neff≥Nthres

Otherwise，resampling is conducted based on the importance.

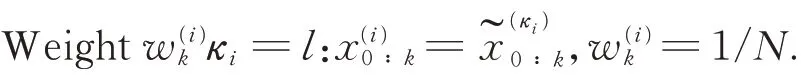
（5）State estimation

where x0∶kis the state variable of 0 ∶k；y1∶ka variable value that is observed at the time k；p(x0) the initial value of the prior density；q(xk|x0∶k-1，y1∶k)the importance function；p(xk|xk-1) the state transition probability density of the system；p(yk|xk)the observation likelihood probability density of the system state；and Nthresthe threshold for measuring the degree of particle degradation.

2 Life Prediction of Rolling Element Bearings Based on SSM in different Degradation Stages and PF

2.1 Establishment of SSM based on Paris formula and Foreman formula

Since the data of current SSM are derived from equipment operation condition information from the monitor system and the uniqueness of the prediction model，the accuracy of these models is comparatively low. To address this problem，specific SSM for different degradation stages is proposed with the transfer of physical data to SSM followed by modification according to the Paris formula and the Foreman formula.

2.1.1 Improved derivation of Paris formula for the second stage

The Paris formula describs the stable expansion law of the fatigue crack，particularly during the second stage of crack propagation. The pure physical data used in the theoretical formula is difficult to obtain and calculate.

The common Paris formula is as follows

where l is the length of the crack；N the number of stress cycles；C the material constant；and Δk the stress intensity factor.

The basic types of cracks are classified into three types：Opening mode，sliding mode，and anti-plane shear mode. Since the first type occurs most frequently，the first type of stress intensity factor formula can be used to calculate

where σ is the magnitude of bearing stress and a the length of the horizontal displacement of the load area of the bearings.

Since

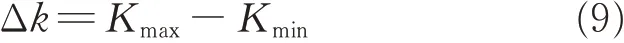
Eqs.（7）—（9）can be combined to derive

According to Eq.（7），the material value n is related to the experimental condition and the material of experiment bearing because σ is related to the load q and the vibration value is influenced by a. n is variable when the experiment condition or the material change.

The modified state equation in the second-stage SSM is proposed as described in Eq.（11）.

where Vdqis the current vibration value；Vnrthe vibration value of normal operation；Northe stress cycle times at the beginning of degradation；V the eigenvalue of the bearings；V(t+1) the eigenvalue of the bearings at the time of t+1. The transferred disturbance of w(t) at time t is the value of the process noise vector generated during the operation of the bearings. k1and m are material coefficients that can be changed according to the material characteristics and experimental environment；and q is the load.

2.1.2 Improved derivation of Foreman formula for the third stage

The rolling bearings prediction is focused on the second stage，and the third-stage rapid expansion of the crack is neglected，increasing the potential error of the prediction result. To solve the above problem，Foreman proposed the Foreman formula in 1976[9]. For the situation when a crack expands rapidly，the Foreman formula is as follows

where Kcdenotes the fracture toughness of materials and R the stress ratio.Here

where Kminis the minimum value of the equal amplitude alternating load and Kmaxthe maximum value of the equal amplitude alternating load.

The crack growth rate increases rapidly when Kmax→Kc，as derived from Eqs.（12）—（13）

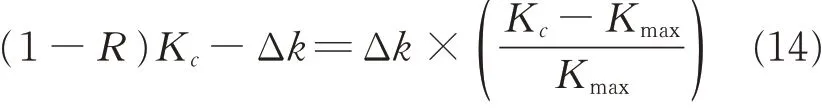
Since the calculation of the value K is related to the force and the vibration value also can reflect the force，we can change the value K to the vibration value Ved，where the Veddenotes the vibration stop threshold. Therefore，Eq.（12）can be transformed as shown in Eq.（15）

The state formula in the third-stage SSM is proposed as shown by Eq.（16）.

The parameters in Eq.（16）are the same as the parameters in the second-stage SSM.

The observation equation for the degradation stages is as Eq.（17）

where y(t+1) is the final state prediction value while v(t) the observation noise vector generated during the operation of the bearings.

SSM in different degradation stages combines the fracture mechanic modeling approach with the data-driven method，which eliminates the problem of the large predicted trajectory deviation due to the single prediction model，and thus improves the accuracy of the prediction results.

2.2 Process of the SSM prediction stages

The flow chart of the procedure is presented in Fig.1 and illustrates the process of extracting eigenvalue and force load data from the operation state of the rolling element bearings，establishing SSM for the different degradation stages，using PF to predict the trend value of the eigenvalue for the rolling element bearings，and calculating the life prediction of the rolling element bearings. The detailed steps are as follows：

Fig.1 Life prediction process for rolling element bearings

（1）The running state vibration signal of the rolling element bearings must be collected，and from this signal，the eigenvalue is extracted.

（2）The alarm threshold，the third-stage degradation threshold，and the stop threshold are set as the initial point of the prediction，the cut-off point for the second and third stages，and the cut-off point of the prediction，respectively. According to the standards of ISO2372 and ISO7919，the vibration standard is divided into A，B，C，and D regions，and each region has an upper limit value. The setting alarm threshold is 1.25 times as much as the upper limit of the B region，and the third-stage degradation threshold is 1.25 times of the upper limit of the C region.

（3） The eigenvalue is incorporated into the rolling element bearing life prediction algorithm when it is greater than or equal to the alarm threshold.

（4）The initial value of the PF algorithm is set.

（5）The predicted step value is set to 10，establishing the SSM. The material constants k1and m of the SSM are set according to Ref.[14]and Eq.（11）. The initial value of these material constants are 2.0 and 1 × 10-3，respectively.

（6）When the eigenvalue is less than or equal to the third-stage threshold of deterioration，the model parameters are updated by using the nonlinear least square method combined with the second-stage SSM，resulting in the second-stage model，which is consistent with the actual running state.The model parameters are subsequently updated by using the nonlinear least square method combined with the third-stage SSM， resulting in the third-stage model that is also consistent with the actual running state.

（7）PF is used to predict the trend of the eigenvalue.

（8）When the predicted eigenvalue is less than the parking threshold，the trend of the eigenvalue can be predicted in a loop. The result of the rolling element bearing life prediction should be output at the prediction time.

3 Experiment and Prediction Analysis

3.1 Experiment

Analysis was conducted by using previously reported full life cycle vibration data[15]produced at the University of Cincinnati in the United States.The experimental apparatus is shown in Fig.2.

Fig.2 Experimental device

The bearing test bench was driven by an AC motor. The speed of the test bench was 2 000 r/min，and the shaft and the bearings were applied to 6 000 pounds of radial load. The acceleration sensor was installed in the horizontal and vertical direction of the bearings.

The experimental data for the bearings[15]were classified into four groups，and we adopted the inner fault data and the first set of sample data. The duration of the experiment was 34 d11 h40 min. To ensure that the data reflected the smooth operation of the rolling element bearings，we adopted data from the previous 32 days after the elimination of serious degradation points. The observable changes of the inner ring of the bearings before and after the experiment are shown in Fig.3，and the detail of the sensors is shown in Fig.4.

Fig.3 Contrast before and after the experiment

Fig.4 Sensor placement

3.2 Acquisition of experimental data and extraction of eigenvalue

The data acquisition system adopted a 6062E data acquisition card （NI Corporation， United States）. Data was collected with 2 000 sampling points at a sampling frequency of 20 kHz，allowing the collection of a set of data at intervals of 10 min.

For the collected data，a wavelet packet energy extraction method[16]was used to obtain the specific frequency band energy at different times. The performance of energy impact was obvious under 1 kHz and a Chebyshev filter was used with a 1 kHz cutoff to obtain high frequency and low frequency signal of the rolling element bearings with time. Then we extracted the variance，peak to peak value，waveform index，peak index，impulsion index，margin index，skewness index，kurtosis index，effective peak value of acceleration，high frequency effective peak value，low frequency effective peak value，envelope spectrum peak value，and 12 characteristic indices.The envelope spectrum peak value is sensitive to the degradation process of the rolling element bearings，and it can be determined using a feature evaluation algorithm and then used as the eigenvalue for the rolling element bearing life prediction. The evaluation results are shown in Table 1.

Table 1 Distance evaluation factor of the characteristic indices

3.3 Analysis of predicted result

The envelope spectrum peak value was normalized，and the alarm threshold，threshold of the third-stage degradation， and the stop threshold were，set to 3.0，7.0，and 9.0 m/s2，respectively，according to the standard requirements described in Section 2.2. According to Section 2.2，an initial value k1of 2.0 and an initial value m of 1 × 10-3were used，and the noise w(t) and v(t) were adopted according to a normal distribution. To avoid a large influence of a weighted value，the numerical range was below 1. For an envelope spectrum peak value greater than or equal to the warning threshold，rolling element bearing life prediction is performed according to the process shown in Fig.1.

The model parameters were adjusted by calculation with the least squares method，and the parameter convergence process is shown in Fig.5.

Fig.5 Convergence process of the model parameter

After obtaining the model parameters，the rolling element bearing life was predicted by using the method described in Section 2.2 and SSM for different degradation stages and the PF algorithm.

There is regular adjustment of the model parameters during the process of rolling element bearing life prediction. To assess the validity of SSM during different degradation stages，the prediction model was used to predict the life of rolling element bearing life during degradation. The predicted results for different degradation stages are shown in Fig.6.

We next compared the SSM for different degradation stages with the Gamma model，which is the preferred method for describing the product degradation process and the single second-stage model. To comprehensively evaluate the effect of prediction results of different models，we calculated the root mean square error（RMSE），the mean absolute error（MAE），the variance absolute error（VAE），the mean relative error（MRE）and the variance relative error（VRE）），as shown in Table 2.

Fig.6 Rolling bearing life prediction result

Table 2 Evaluation of life prediction effect for the different models

It can be seen from Fig.6 that the rolling element bearing life prediction method based on SSM in different degradation stages and PF can accurately reflect the degradation process of the rolling element bearings. The predicted degradation curve is close to the actual degradation curve，and this method is feasible. During the process of prediction，the accuracy of the predicted result improved gradually，and the predicted degradation trend becomed closer to the actual degradation trend because the parameters of the model were updated regularly，allowing correction of the model with time.

Table 2 shows the evaluation results of the life prediction effect of different models. The life prediction method based on SSM for different degradation stages shows better accuracy and precision than the second-stage model and the Gamma model，because of the inclusion of SSM based on different degradation stages，including the second-stage and the third-stage degradation of the rolling element bearings. Meanwhile， the degradation path becomed closer to the actual degradation path，suggesting the improved model can accurately reflect the deterioration process of the rolling element bearings.Since the Gamma model is based on a probability method，the calculation results are necessarily dependent on the prior probability distribution，and the method has a low degree of relativity with the degradation mechanism of rolling element bearings.

4 Conclusions

In order to improve the accuracy of models for the life prediction of rolling bearings，we propose a prediction method based on SSM in different degradation stages and PF，including three rolling element bearing life prediction methods，and improving the Paris formula and Foreman formula according to the degradation mechanism of rolling element bearings. Additionally，this method incorporates the running status information of rolling element bearings and uses the PF algorithm to predict the real lifetime of the rolling bearings. This approach effectively improves accuracy of life prediction thanks to the physical degradation model of rolling bearings.

The experimental evaluation results show that the rolling element bearing life prediction method based on SSM for different degradation stages and PF is more accurate than the traditional prediction method based on the Gamma model and the PF.Generally，this work provides a new effective method for life prediction of rolling element bearings.