Reflected Wavefront Modulation with Phase Array by Using Acoustic Metasurface

CHENG Yong，LIANG Qingxuan，CHEN Tianning，GUO Jianyong

State Key Laboratory for Manufacturing Systems Engineering，School of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，P.R.China

Abstract: Acoustic metasurface has attracted increasing attention due to the ability of manipulating the transmitted and reflected phase of waves to generate various acoustic functionalities with planar layer of sub-wavelength structure.We design an acoustic metasurface with a semi-closed and nested slotted tube array，and it possesses the capacity of modulating the reflected phase with sub-wavelength thickness（about λ/23）. The reflected phase shifts can be obtained from 0 to 2π by different rotation angles of internal slotted tubes. The theoretical results agree well with the numerical results by a finite element method. The results show that some excellent wavefront manipulations are demonstrated with the phase array by using acoustic metasurface such as anomalous reflection and sub-wavelength flat focusing. The design may offer a path for acoustic manipulation and promote the potential applications of acoustic metasurface in low frequency noise control，acoustic imaging and cloaking.

Key words: acoustic metasurface;anomalous reflection;phase gradient;semi-closed and nested slotted tube

0 Introduction

The precise manipulation of wavefront has attracted increasing attention over the last few decades，and great progress has been made since metamaterials was first proposed. The two-dimensional equivalent of metamaterials，i.e. the so-called metasurface，brought more possibilities in manipulating waves.Acoustic metasurface（AM），which composed of unit cells with thickness much smaller than the wavelength，has attracted tremendous attention due to the ability of tailoring the scattered wavefront into arbitrary desired shape. AM reveals the huge applications at low frequency noise control[1-5]，acoustic imaging[6-7]，unidirectional sound transmission[8-11]and cloaking[12-15]. According to the generalized Snell’s law，the modulation of wavefront by AM requires the phase discontinuities with the phase shifts covering 2π span by unit cells of metasurface. At the moment，some investigations for the phase control by AM have been acquired such as membrane-type AM[16]，Helmholtz resonator AM[17-23]and spacecoiling AM[24-27]. However，the membrane-type AM is difficult to realize in practice through the membrane stress. The complex structure of space-coiling AM leads to the difficulty of the continuous modulation of the phase shifts. For the Helmholtz resonator AM，the simple structure and phase shifts can be manipulated continuously. Li et al. proposed the AM by hybrid structure consisting of a straight pipe of height and four Helmholtz resonators[22-23].The area of necks of Helmholtz resonators serves as designed parameter to realize the reflective AM based on split hollow sphere and double-split hollow spheres[17-19]. The reflection phase of the split ring resonators can be controlled by altering the geometries of the spilt and cavity[28]. However，this may not be an effective method to overcome the drawback of relative bulky dimensions of Helmholtz resonators. Meantime their acoustic behaviors highly depend on their dimensions in the previous studies. So the Helmholtz resonators have not been considered to be good candidates for ultrathin metasurface[12].

In this paper，a new type of unit cell structure of Helmholtz resonators has been proposed，which is semi-closed and nested slotted tube（SANST）.The SANST is one of Helmholtz resonator structures，which has to wrestle with the challenges of relativity bulky volume and their acoustic behaviors highly depending on their dimensions. This structure breaks the symmetry of nested slotted tube and extends the length of the necks with Helmholtz resonators. Therefore，the relativity bulky volume can be decreased. Meanwhile，the extended length of the necks with Helmholtz resonators can make their acoustic behaviors less depend on their dimensions.In this study，we design the AM with the SANSTs structure with sub-wavelength thickness（about λ/23）. By different angles between inner and outer seam of slotted tube（the length of the necks with Helmholtz resonators），the unit cells have the properties of arbitrary steering of the reflection phase shifts ranging from 0 to 2π. With the phase array of AM，the capability of general modulation of the reflected wavefront can be obtained. It is demonstrated that the SANSTs can manipulate the acoustic wavefronts at a broadband frequency range. The anomalous reflection and acoustic planar focusing effect are achieved by the present metasurface. The new unit cell structure of Helmholtz resonators may offer a new path to design relative small scale of Helmholtz resonator AM.

1 Design of AM Unit Cell

The schematic sketch of the AM unit cell，as shown in Fig.1（a），is composed of nested slotted tube.The interspace of nested slotted tube is closed off by the wall，which is located on the left side of the outer slotted. The radius of the outer slotted is r. The width of the seam between the outer and the inner slotted is w，the tube wall thickness is t，the width of the space between the outer and the inner slotted is w0. The angle between the inner and the outer seam of the slotted tube is α. The main idea is that the phase shift is tuned by coupling the cavity of SANST and the interspace of the nested slotted tube，while the bottom rigid wall is used to enhance reflection. Consider that the work wavelength is considerably larger than the unit cell structure’s dimension. The acoustic characteristics of the unit cell can be understood by the lumped parameter model[29].Based on the lumped parameter model，the imaginary parts of acoustic impedance of unit cell can be expressed[29]

where ρ0is the air density；c0the sound speed in air；V=π(r-2t-w0)h the volume of the cavity of SANST，here h is the height of vertical direction on paper； l=α(r-t-w0/2)+2t+w0the length of interspace of nested slotted tube；and S0=w0h the area of seam. When Z0→0，the resonance frequency of SANST can be calculated by f=The imaginary parts of acoustic impedance of unit cell can be expressed as Z0=iρ0c0/(2ah)tan[ϕ(x)/2][30]. Substituting the specific acoustic impedance into Eq.（1），the reflected phase can be obtained as

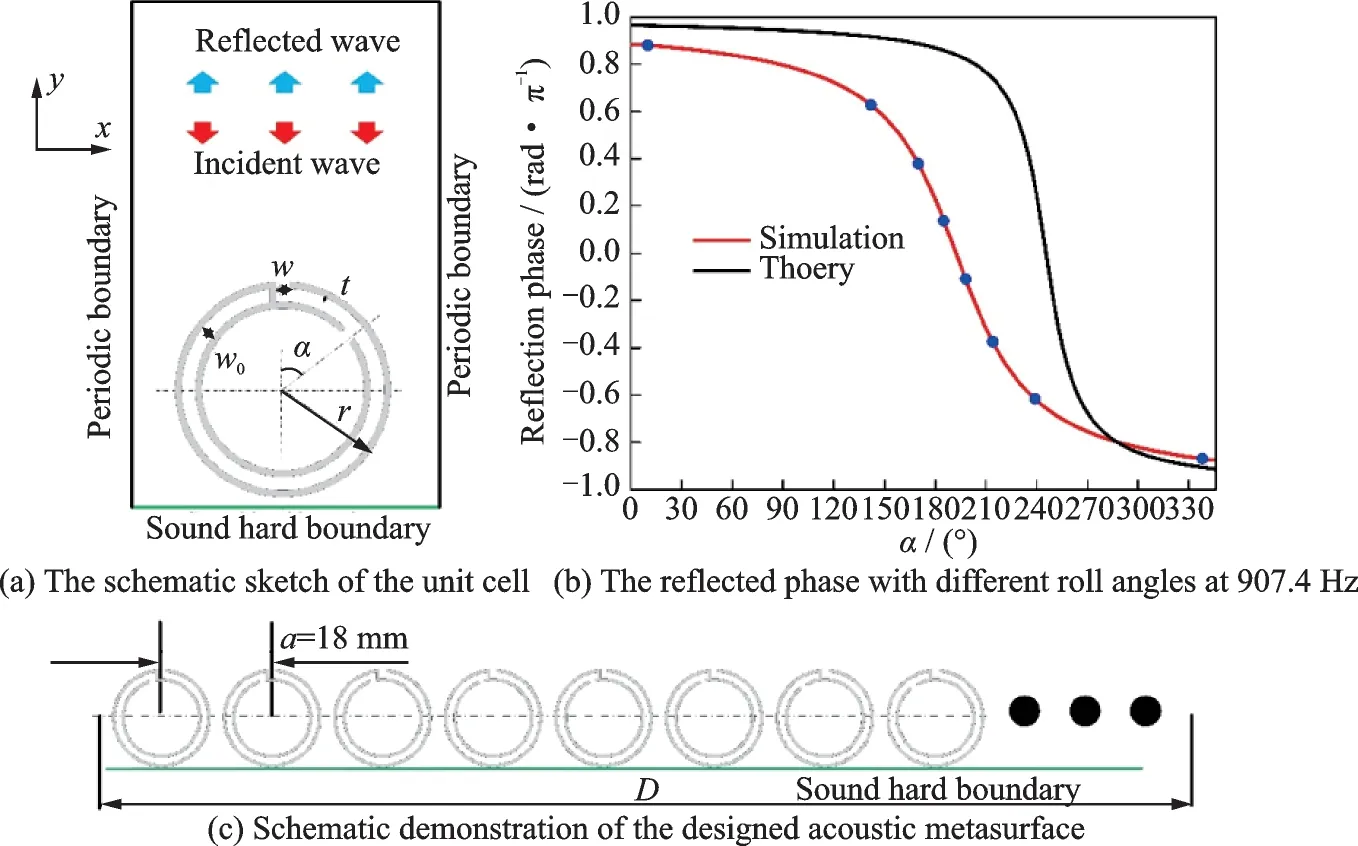
Fig.1 Illustration of the designed acoustic metasurface

To demonstrate the properties of modulation of phase shifts ranging from 0 to 2π capability of the reflected wavefront of the SANST with relativity small modules at designed frequency of 907.4 Hz，the geometric parameters of SANST can be selected as r=8 mm，w0=1 mm，w=1 mm，t=0.5 mm. By simultaneously tailoring α from 0° to 346°，one can obtain the corresponding reflection phase shifts covering 2π range at the designed frequency of 907.4 Hz. The reflection phase is presented in Fig.1（b），where the theoretical results and the numerical results are basically compatible. The reason of the deviation is ignoring the length correction factor of Helmholtz resonance. The phase shift of the unit cell can be adjusted with the step of π/4 by rouing the inner slotted tube and the corresponding angles have been marked by solid dots in Fig.1，which means 10°，142°，170°，185°，198°，214°，239°，and 338°. In the simulation，the AM is composed of eight unit cells mentioned above. The phase array can be tuned by different combinations with eight unit cells of a supercell（the length is D）to realize the AM，as shown in Fig.1（c）. Here，the choice of simulation software is COMSOL multiphysics software based on a finite element method.The background material is the air with the mass density of 1.21 kg/m3and sound speed of 343 m/s.The material of the SANST in simulation is steel.Therefore，the boundaries between the SANST and air can be regarded as rigid boundaries with impedance mismatch. The side face is set as periodic boundaries，as shown in Fig.1（a）. The top surface is plane wave radiation boundary with incident wave amplitude 1 Pa，the y-direction transmitted boundary is set as sound hard boundary. The downward arrow indicates the incident waves and the upward arrow indicates the reflected waves. Note that we ignore the intrinsic loss of the structure because the viscous boundary layer of the air-hard wall interface[28]is only 0.07 mm，much smaller than the height of the air passage，where γ ≈1.7 × 10-5Pa·s denotes the air viscosity.

2 Realization of Anomalous Reflection by Using AM

2.1 Reflection waves with different phase gradient AM

The control of reflection wave needs to follow the Snell’s law via appropriately introducing a supercell with the phase gradient at the interface between the AM and air. The behavior of reflection wave follows the generalized Snell’s law of reflection[19]

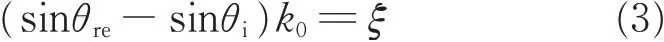
where θiand θreare the incident and reflected angles，respectively；is the wave vector in air；λ the wavelength；andthe phase gradient on the AM along x-axis. The angle of reflection wave can be obtained by Eq. （3） as θre=can be tuned by designing suitable phase profiles along AM.

In order to investigate the reflection wave behavior with different phase gradient of AM，we simulated the reflected acoustic field at 907.4 Hz，when the normal incident is plane wave with the phase gradient of ξ = π/216，π/288，π/360 rad/mm，as shown in Figs.2（b），（d）and（f）. The thickness of the supercell is 16 mm（about λ/23），which is at the deep wavelength scale.In the simulation，the reflected angles of 60°，41°，31.5°，which agree with the theoretical results of the generalized Snell’s law with the angles of 61°，41°，31.7°，respectively. The results indicate the angle of reflection wave can be controlled via the appropriate phase gradient AM.We also calculated a normal material with the corresponding slant angle θre/2 with the phase gradient of ξ = π/216，π/288，and π/360 rad/mm to investigate the effect of the reflection of the AM. The length of acoustic prism is the same as the phase gradient AM. The pressure field distributions of the reflected waves are shown in Fig.2，and the simulation results agree well with the reflected effect of phase gradient AM. These results illustrate that the integration of smart AM based on SANST in flat area can realize the acoustics illusion of slope of any angle.

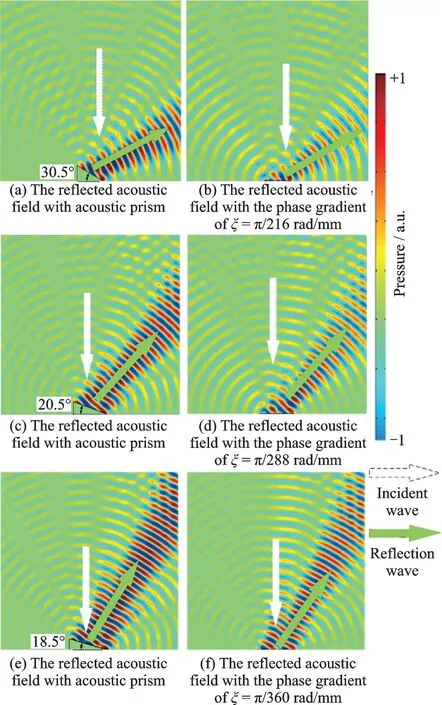
Fig.2 The reflected acoustic field distribution at 907.4 Hz

2.2 Discussion of broadband property of phase gradient AM

In this section，the frequency dependence of the AM was studied. The AM of phase gradient of ξ = π/288 rad/mm is selected as a research object which is designed at 907.4 Hz. The simulations of the phase gradient of ξ = π/288 rad/mm of AM is conducted from 840 Hz to 1 000 Hz for the cases of plane wave normal incident，and the acoustic pressure field distributions of the reflected waves are shown in Fig.3. The results imply that the reflection waves could be manipulated from 850 Hz to 990 Hz，and the engineered AM is capable of steering sound waves in a broadband frequency range，although the phase profile is only designed for a specific frequency. The reflected angles in simulation are 45°，41°，39°，and 36.9° which agree well with the theoretical values of 44.8°，41.4°，38.8° and 36.5° at the frequencies of 850，900，950，and 990 Hz，respectively. It is obvious that the anomalous reflected angle decreases as the frequency increases. This phenomenon follows the principle of the generalized Snell’s law. When the incident wave frequency is f0＞990 Hz or f0＜850 Hz，the phenomenon of anomalous reflection lose efficacy，as shown in Figs.3（e），（f）. The results show that the anomalous manipulation of the reflected wave with AM is effective in a broadband frequency range from 850 Hz to 990 Hz.

Fig.3 Reflected acoustic pressure field distribution of AM with the phase gradient of ξ = π/288 rad/mm

3 Sound Focusing of Planar Lens by Using AM

Here，further possible application of this model has been demonstrated. The ultrathin sound focusing planar lens can be designed by rearranging the unit cells of the AM. The focal length f is an important parameter for the design of sound focusing planar lens. For the given focal length f，the hyperbolic phase configuration along the AM can be ascertained by the following equation[31]

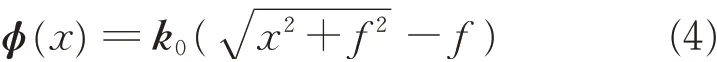
where k0is the wave vector and the focal length is chosen to be f = 1 500 mm. The acoustic metasurface is constructed according to Eq.（4）. The simulated region is from 0 to 4 000 mm along the Y-axis，and from -1 647 mm to 1 647 mm along the Xaxis. The length of the metasurface is 3 294 mm.The metasurface is composed of 183 unit cells.When incident plane waves impinging normally on the metasurface，the spatial distribution of the reflected sound field for the planar lens perfectly matches that for the ideal concave spherical mirror at 907.4 Hz，as shown in Figs.4（a）—（e）. The transverse cross - section intensity distribution at X =0 mm along the Y-axis，for the ideal concave spherical mirror and the planar lens by using AM，is shown in Figs.4（c），（f）. The focal length is perfectly matched. The intensity of pressure at the focal spot is nearly 15 times larger than that of the incident waves，which shows excellent focusing effect.

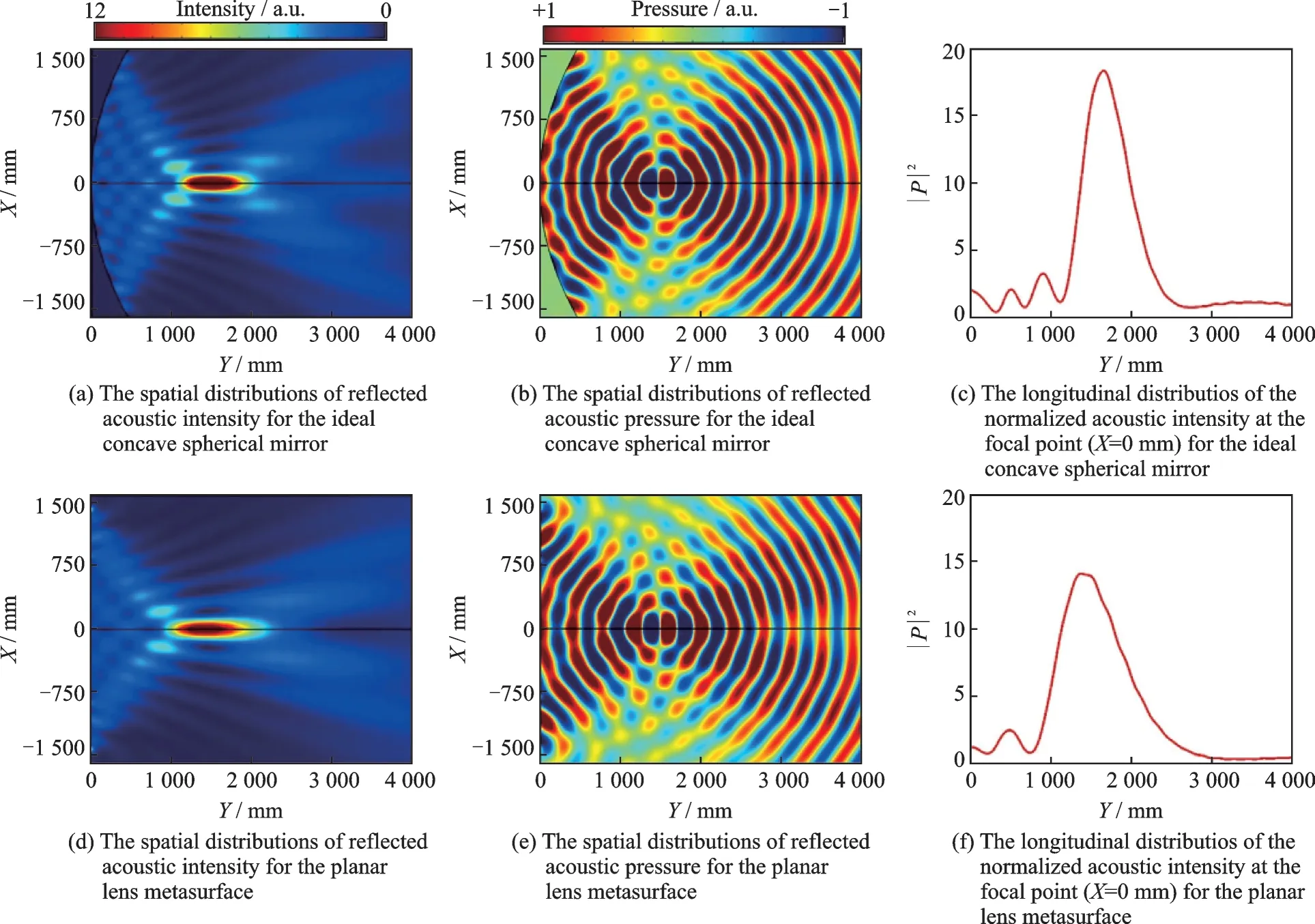
Fig.4 Numerical illustration of the acoustic metasurface lens

4 Conclusions

We have designed a new type of AM structure with a semi-closed and nested slotted tube array at the subwavelength scale. It can realize complex acoustic wavefronts modulation with the phase array by using acoustic metasurface. The simulation results agree well with the theoretical predictions for wavefronts manipulation of unit cell. By properly selecting α of unit cells，the phase file can be obtained to assemble metasurface. The simulation results also show that the designed AM exhibits the anomalous reflection in a broadband frequency ranging from 850 Hz to 990 Hz. Furthermore，acoustic focusing lens can be constructed by using the hyperbolic phase gradient. With the presented ultrathin AM in the study，acoustic potential applications，such as low frequency noise control，acoustic imaging and cloaking devices，are promising in the future.

AcknowledgementsThe work was supported by the National Natural Science Foundation of China (No.51575431),the China Postdoctoral Science Foundation Funded Project(Nos.2014M550485, 2015T81019), the Fundamental Research Funds for the Central Universities (No.xjj2015098),and the Shaanxi Province Postdoctoral Science Foundation Funded Project.

AuthorsMr. CHENG Yong is pursuing the M.S. degree in mechanical engineering from Xi’an Jiaotong University，China.His research focuses on acoustic metamaterials.

Dr. LIANG Qingxuan received the B.S. degree in material science and engineering and the Ph.D. degree in mechanical engineering from Xi’an Jiaotong University in 2003 and 2012，respectively. Now he serves as an associate professor at Xi’an Jiaotong University. His research focuses on 3D printing technology and its application on metamaterials.

Prof. CHEN Tianning received the B.S. and Ph.D. degrees in mechanical engineering from Xi’an Jiaotong University in 1982 and 1996，respectively. Now he serves as a full professor at Xi’an Jiaotong University. His research focuses on the field of vibration and noise control.

Mr. GUO Jianyong is pursuing the M.S. degree in mechanical engineering from Xi’an Jiaotong University，China. His research focuses on metamaterials.

Author contributionsMr. CHENG Yong conducted the theoretical and simulated work. Dr. LIANG Qingxuan proposed the idea and prepared this manuscript.Prof.CHEN Tianning and Mr. GUO Jianyong contributed to the analysis.All authors contributed to the discussion.

Competing interestsThe authors declare no competing interests.