Routh table test for stability of commensurate fractional degree polynomials and their commensurate fractional order systems

Sheng-Guo WANG ,Shu LIANG ,Liang MA ,Kaixiang PENG

1.College of Engineering and College of Computing and Informatics,University of North Carolina at Charlotte,NC 28223-0001,U.S.A.;

2.School of Automation and Electrical Engineering,University of Science and Technology Beijing,Beijing 100083,China

Received 22 June 2018;revised 18 November 2018;accepted 4 January 2019

Abstract A Routh table test for stability of commensurate fractional degree polynomials and their commensurate fractional order systems is presented via an auxiliary integer degree polynomial.The presented Routh test is a classical Routh table test on the auxiliary integer degree polynomial derived from and for the commensurate fractional degree polynomial.The theoretical proof of this proposed approach is provided by utilizing Argument principle and Cauchy index.Illustrative examples show efficiency of the presented approach for stability test of commensurate fractional degree polynomials and commensurate fractional order systems.So far,only one Routh-type test approach[1]is available for the commensurate fractional degree polynomials in the literature.Thus,this classical Routh-type test approach and the one in[1]both can be applied to stability analysis and design for the fractional order systems,while the one presented in this paper is easy for peoples,who are familiar with the classical Routh table test,to use.

Keywords:Fractional order systems,stability,commensurate fractional degree polynomials,Routh table test

1 Introduction

Fractional order systems(FOSs)have attracted increasing attention and gained growing development during the past few years due to the FOSs existence in physical experiments[2,3],and the development of flexible methodologies for easy study and favorable performance of fractional order control systems[1-5].It is noticed that the research of fractional-order circuits and systems has been as an emerging interdisciplinary research area in the circuits and systems because of physical FOS behavior existing in real capacitors[3].One core research subject of FOSs from the control viewpoint is the stability analysis and synthesis.In the research field of systems and control,synthesis methods have been fertilized by using fractional order system analysis to achieve flexible and robust controllers[3,4,6,7].Particularly,commensurate FOSs(CFOSs)have become an important type of FOSs because CFOSs share similar structures to the integer order dynamic systems and maintain the characteristic of general FOSs[8].

Routh table test is well-known for the stability analysis and synthesis of control systems,which provides zeros distribution of the system characteristic function via finite steps of simple algebraic calculations.However,the classical Routh test is not directly applicable to FOSs.Thus,despite those substantial achievements of FOSs,the Routh table test[9,10],as the most useful stability test with the lowest calculation load for classical integer order systems,is rarely investigated for FOSs,except our recent work[1].

Moreover,the advanced root(zero)finding methods for any general polynomials with degrees greater than four are approximate methods as well-known from Galois theory as discussed in[1].Even powerful Matlab tools may also give mistake roots(zeros)in the right-half plane for a stable integer polynomial[1].However,the Routh table can give correct results for the root(zero)distribution of any general integer degree polynomials because it is a strictly mathematically proved method,not an approximation method.This fundamental merit is significant as Routh-type methods for polynomials.

Therefore,what is current status in the Routh-type tests for the commensurate fractional degree polynomials?Thus,let us briefly review[1]for it.The main contribution of reference[1]is as the first paper in the literature:1)to ask if there are Routh-type tests and methods for general commensurate fractional degree polynomials(CFDPs);2)to present the uniform Routhtype tests and formulas for zero distribution of CFDPs and integer degrees polynomials(IDPs);3)to handle the singular cases easily and correctly as much better than the classical Routh table test;4)to reveal the symmetric property of zero distribution in the second singular case for the CFDPs;and 5)the last but not least,to present the strict theoretical mathematical proof for their Routh-type table tests and methods.On the other hand,the Routh-type table tests in[1]need to check the sign change numbers of both head column and non-zero tail“column”(i.e.,non-zero tail sequence)in the table.

Thus,it is natural to ask if there is a possible approach to check only the sign change number of the head column of the Routh-type table for CFOSs as the classical Routh table test.If it is possible,what kind of that Routhtype table will be?

Motivated by the above discussions,this paper derives a method such that the classical Routh test can be applicable to CFOSs.To be specific,given a CFDP,we propose an auxiliary integer degree polynomial(AIDP)and use the classical Routh test on this AIDP for the CFDP.Then the zero distribution of the original CFDP is obtained via quite simple calculations of the classical Routh test on the AIDP.Thus,we give an affirmative answer that the classical Routh table test can be extended for CFOSs by applying this new method on the AIDP.Also,this new method for CFOSs inherits the merits of the classical Routh test for integer order systems,revealing the relationship between the coefficients and zero distribution,and how these coefficients will impact the system stability.Note that such an analytical result is not shared by computing zeros numerically for the stability checking.On the other hand,it also inherits the same special needs of classical Routh test to treat special singular cases,i.e.,the first type of singular cases and the second type of singular cases,even they happen together.In order to solve this well-known singular case problems in the classical Routh table,many other alternately modified methods are developed for it,e.g.,in[1,11-13].In these singular cases,the reference methods in[1]have their benefit as the simplest way to treat these special cases and with the fewest rows.

The main difference between the method proposed in this paper and the only comparable existing method in[1]is listed as follows.a)The proposed method is to use the classical Routh table test,while the method[1]uses the Routh-type table test for CFDPs;b)The proposed method uses the auxiliary integer degree polynomial(AIDP),while the method[1]does not use AIDP;c)The proposed method only checks the number of sign changes in the head column of the Routh table on the AIDP,while the method[1]needs to check the numbers of sign changes in the head column and the non-zero tail“column”(non-zero tail sequence)of its Routh-type table;d)The determination formula of the proposed method is easier than the one in[1];e)On the other hand,the number of the rows in the table may be larger than the one in[1];and f)Both methods are accurate with strict theoretical proofs for their respective objectives.

Thus,the main contribution and novelty of this paper are summarized as follows:

1)as the first paper in the literature to ask if there is a classical Routh test method still valid for general CFDPs;

2)to present an AIDP for the CFDPs and their stability problems;

3)as the first to advance the classical Routh table test on the proposed new AIDP for the CFDP and its stability problems;

4)to develop a new approach via the classical Routh table test for analyzing various systems stability and revealing the relationship between the polynomial data(commensurate order and coefficients)and their zero distributions for the system synthesis;

5)to have advantage of determining the stability of CFDPs via the Routh table as shown in[1],i.e.,an easiest way to determine the stability,while the stability is the first important issue for all systems including the fractional order systems;

6)to have potential applications for fractional order system stability problems and in emerging new areas in view of the broad applications of classical Routh table test for various stability problems in science and engineering[14-16];

7)to present the theoretical proof for the classical Routh table test on the CFDP stability via a similar base proof approach as in[1];and

8)to present an easy and accurate method for stability analysis of CFDPs and fractional order systems compared to all common existing methods which are via essential approximation way by taking direct roots/poles calculation or linear matrix inequality for stability analysis of general fractional degree polynomials and systems,except the method in[1].

Table 1 is for the notations of symbols used in this paper.

Table 1 Notations.

2 Preliminaries

In this section,we introduce preliminary background knowledge of this paper.

A fractional order integrator of degree α has the inputoutput relation as

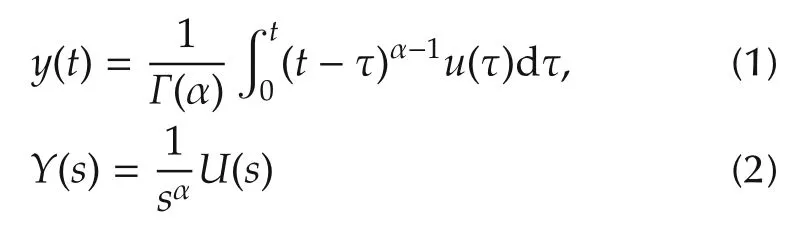
as in time domain and frequency domain respectively,where α ＞0 and Γ(·)is the Gamma function.In contrast to the integer order one,the magnitude curve of a fractional order integrator has flexible slope as-20α dB/dec,determined by the fractional order α.In general,a linear time-invariant fractional order system with single input and single output has its transfer function[8]as

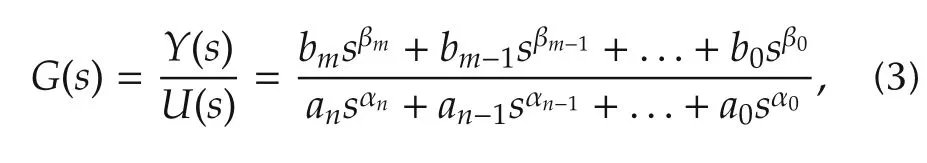
where αn＞αn-1＞...＞α0≥0 and βm＞βm-1＞...＞β0≥0.Either the numerator or the denominator of G(s)is a so-called fractional degree polynomial(FDP).System G(s)is said to be of commensurate order if there exists α ＞0 such that αk=kα,βl=lα for k=1,...,n,and l=1,...,m.Correspondingly,its numerator and the denominator both are CFDPs.A general CFDP can be written as

where the commensurate α ＞0,and k=0,1,...,n.The definitions in(1)-(3)are used to define a fractional order system,where equation(4)may represent its system characteristic polynomial.

The Riemann surface RS is defined aswhere the kth Riemann sheet RSkis defined as RSk≜{s|-π+2kπ ＜arg(s)≤π+2kπ}for any k ∈I.Particularly,the Riemann principal sheet RPS is defined as the central Riemann sheet as RPS ≜RS0={s|-π ＜arg(s)≤π},i.e.,k=0.

The transfer function G(s)has its single-valued branch on each RSk.Specifically,the branch in the RPS is utilized to describe the fractional order system,because it determines the Cauchy principal value of the integral corresponding to the inverse Laplace transformation of G(s).The direct application of residue theorem implies that only the poles of G(s)in the RPS determine the system stability and dynamic performance.In particular,the following lemma with respect to stability of G(s)is well-known.

Lemma 1[17,18] The following two stability criterions hold.

Criterion 1:A fractional system(3)is BIBO stable if and only if its transfer function has no pole in the closed right half complex plane of the RPS,i.e.,nr(F)=0 and ni(F)=0.

Because this paper focuses on the CFOSs stability via their characteristic polynomials,i.e.,CFDPs,therefore different from most existing works based on Criterion 2,only[1]and our test for zeros distribution are associated with Criterion 1 in Lemma 1.Especially,here our proposed method is via the classical Routh table test on the associated AIDP for the CFDP,making its uniqueness.

We describe the key preliminaries as summarized below as the Cauchy index and two lemmas,which will be used to prove our main result Theorem 1 in Section 3.

Lemma 2Consider a function Φ(x)≜f(x)+jg(x):R →C,where f(x)and g(x)are continuous real functions.If Φ(x)≠0 for x ∈(a,b),then its net phase changearg(Φ(x))as x changes from a to b can be calculated by using the Cauchy index as

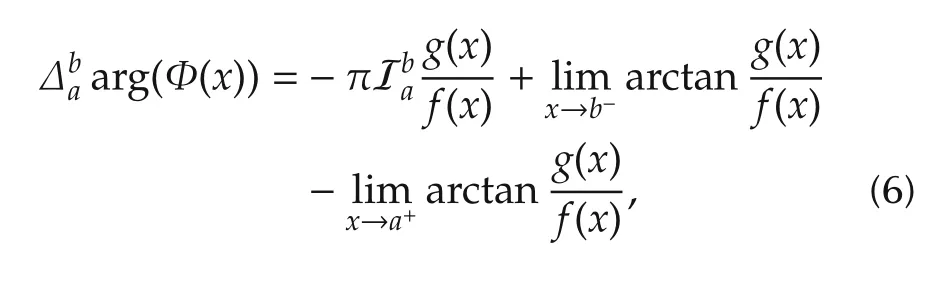
or

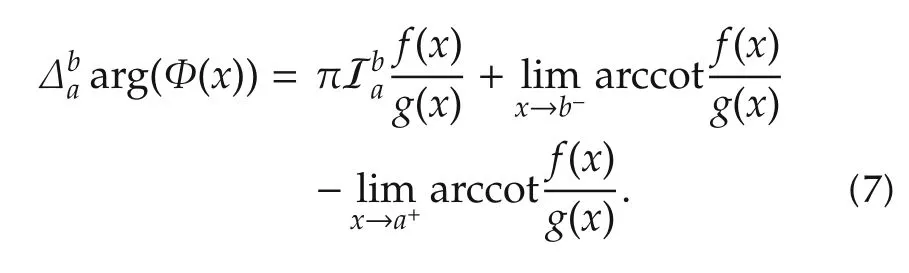
ProofThe phase function can be represented as arg.If arg(φ(x))is continuous in the region x ∈(a,b),then

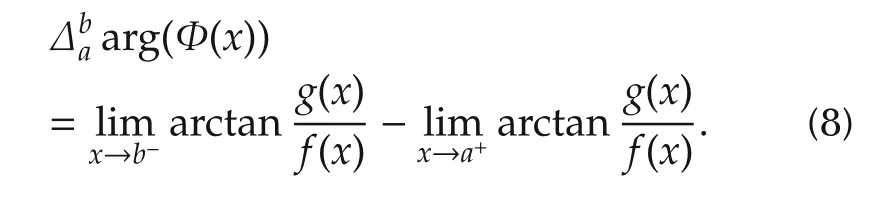
Otherwise,arg(Φ(x))is discontinuous at some points in the region x ∈(a,b).To be specific,as x passes a discontinuous point c ∈(a,b),the phase arg(Φ(x))will have a change of π.Then we can use Cauchy index from a to b to identify its phase change as

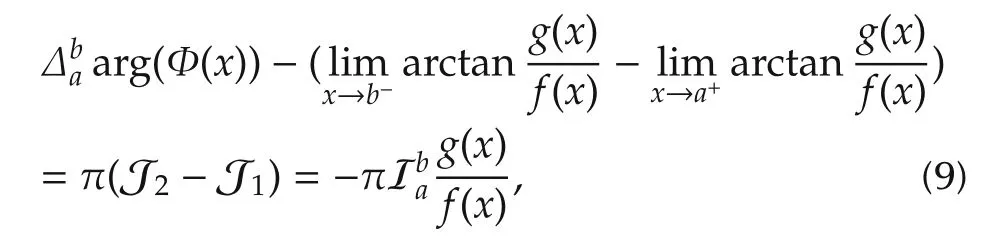
where J1and J2are the jump numbers as in Definition 1.Thus equation(6)holds.Note that the phase function can be also represented asthen equation(7)holds similarly to(6). □

Next we brief famous Routh table as a Lemma 3 here.It refers to[9,10].

Lemma 3(Routh,[9,10]) Consider a real coefficient integer degree polynomial P(s)as

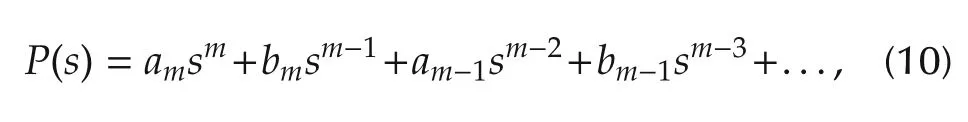
where m is a positive integer number.Then nr(P)and ni(P)can be determined by the Routh table test on P(s)as follows:

i)The number ni(P)is equal to the number of real zeros of d(x)=d(ω)≜gcd(R(P(jω)),J(P(jω))).

ii)The following equality with respect to Cauchy index holds:

Remark 1Lemma 3 basically states that the zeros distribution of integer degree polynomial P(s)in(10)can be calculated via the Routh test,which is a well-known result.Lemma 3 presents an important analytical tool for the zeros distribution via the Cauchy index.

The key features of the proposed approach in this paper are as the same as the classical Routh table test has.Thus,it is easy for readers,who are familiar with the classical Routh test,to use it.

3 Routh test for CFDPs

In this section,we present the result that advances the classical Routh test for CFDPs as Theorem 1.

Theorem 1Consider a commensurate fractional degree polynomial function F(s)as

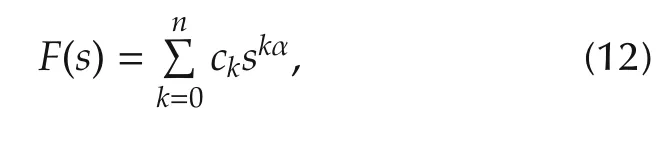
where its coefficients c0,c1,...,cn∈R and c0≠0,cn≠0,and the commensurate α ＞0.Construct an auxiliary integer degree polynomial P(s)from F(s)as

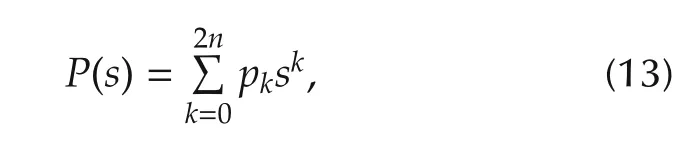
where the coefficients of P(s)are

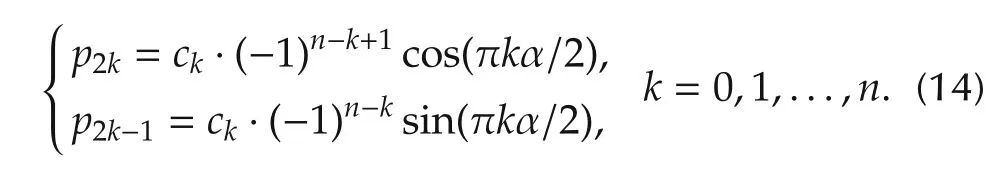
Then we have

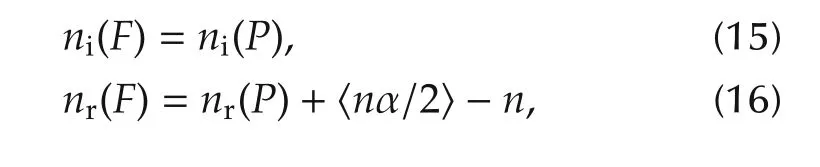
where ni(F)and nr(F)are the numbers of zeros of the CFDP F(s)on the imaginary axis and in the righthalf-plane(RHP)of the RPS respectively,while ni(P)and nr(P)are numbers of zeros of the AIDP P(s)on the imaginary axis and in the RHP of the complex plane respectively,and〈·〉is a round-off operator as x=m+γ,m ∈N,0 ≤γ ＜1,and

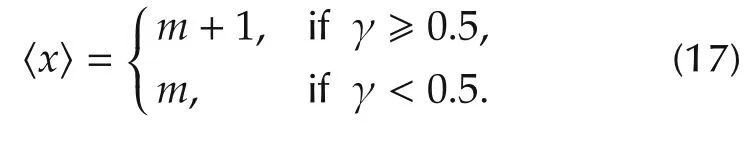
ProofThe approach of the proof is via the Argument Principle(to calculate zeros numbers in the RHP and imaginary axis and phase change of a complex function),the Cauchy index and Lemmas 2 and 3.The considered zeros numbers are ni(·)on the imaginary axis and nr(·)in the RHP of the RPS.The Argument Principle takes the Nyquist path as shown in Fig.1 as Γ1and-Γ2.Notice that the imaginary roots are the roots of the gcd of the real part and the imaginary part of the complex polynomial function.The goal is to prove ni(F)=ni(P),and to present nr(F)by nr(P)and its fractional factor.

Fig.1 Contour of the right half plane in RPS.

The proof consists of the following four steps.The first step is to build the real part and imaginary part of F(s)as s=jω.The second step is to show ni(F)=ni(P)in(15).The third step is to show nr(F)=nr(P)+〈nα/2〉-n in(16)when nα ∉Nodd.Then fourth step is to show(16)when the highest order nα ∈Nodd.

Step 1For ω≥0,let

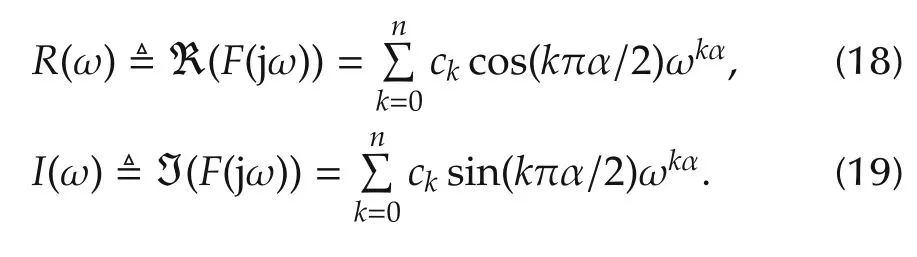
From the bijection transformation x=ωα:R+→R+,let

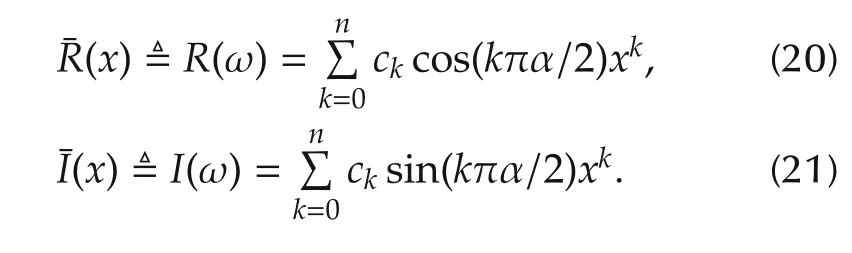
Moreover,let

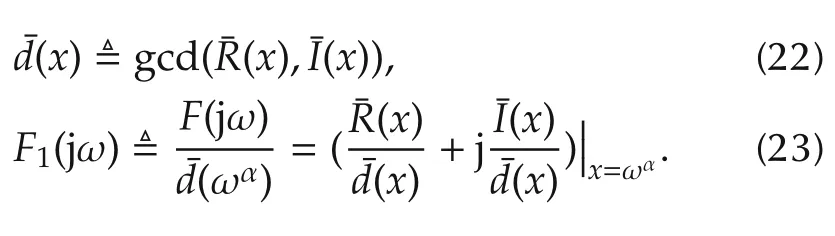
Here the motivation to introduce the bijection transformation from ωto x in(20)and(21)is to absorb the fractional-order α,such that we have an integer-order polynomial in form of x instead of fractional order polynomials in(18)and(19)respectively.It is also helpful to compare it with the AIDP in(13).

Step 2We take the Nyquist path as in Fig.1 that encircles the entire right half plane and excludes pure imaginary zeros of F(s)in(12).Applying the Argument Principle along this Nyquist path,we have

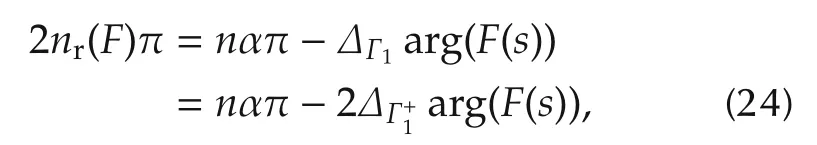
where Γ1is the curve along the imaginary axis from-j∞to+j∞excluding the pure imaginary zeros of F(s)as shown in Fig.1,andis the half of Γ1from j0 to+j∞.Note that F(jω)|ω=0=c0≠0 and F(s)is with real coefficients,i.e.,having conjugate symmetric zeros,and the origin is not a zero of F(s)and F(jω).Meanwhile,we have

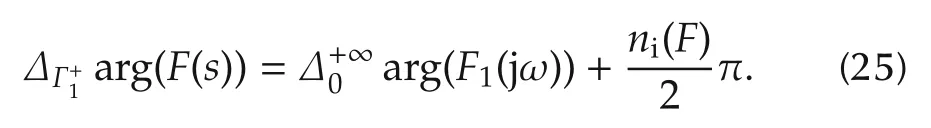
Substituting(25)into(24)yields

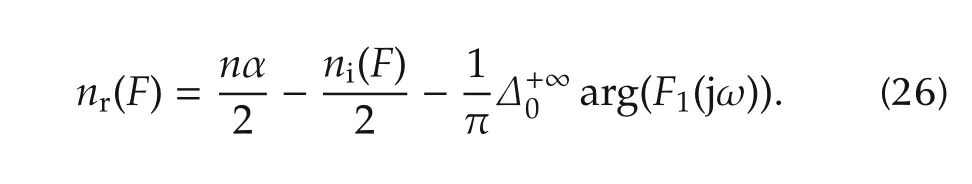
Furthermore,the imaginary zeros of F(s)is F(jω)=0,if and only if(x)=0 for x=ωα＞0 as we notice the symmetric property and consider positive ωhere.Thus,the number of the positive real zeros of(x)is ni(F)/2.

From(20)and(21)of F(s)and the coefficients(14)of P(s),we have ni(F)=ni(P)in(15)based on the statement(i)of Lemma 3,where P(s)is with its α=1.

Step 3Consider the case nα ∈ R+Nodd,i.e.,deg((x))≥deg((x)).From Lemma 2 with equation(6),we have

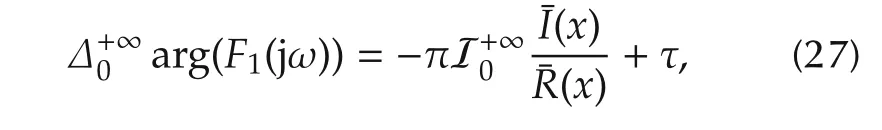
where

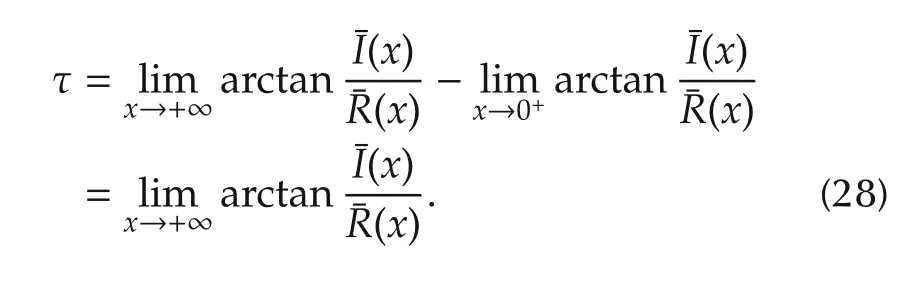
Thus,-π/2 ＜τ ＜π/2.Substituting(27)into(26)yields

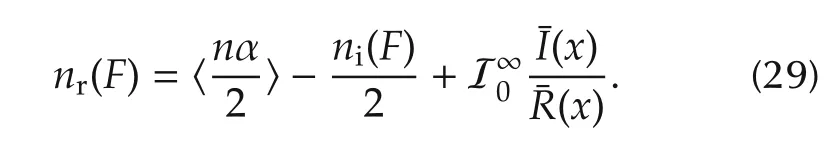
On the other hand,from Lemma 3 with P(s)in(10),we substitute its coefficients(14)into equation(11)that yields

Next,we show the following by the definition of Cauchy index:

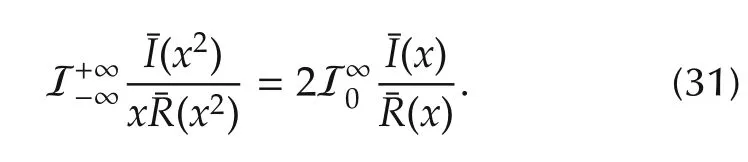
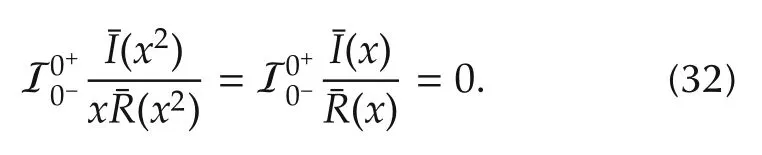
Second,the following is true from the Cauchy index

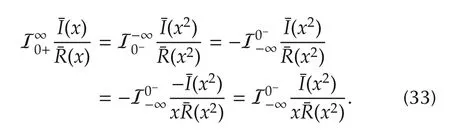
Third,we have

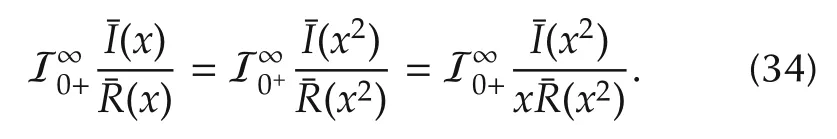
Then(32)-(34)lead to(31).Then substituting(30)and(31)into(29)yields(16)

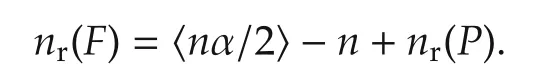
Step 4Finally,we shall show(16)for the remaining case nα ∈Nodd,i.e.,.From(7)in Lemma 2,we have

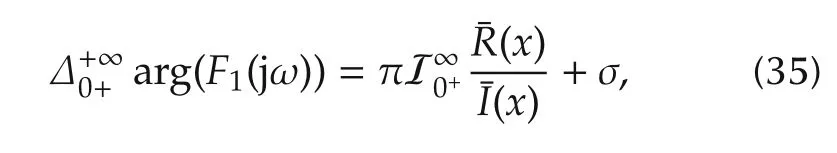
where

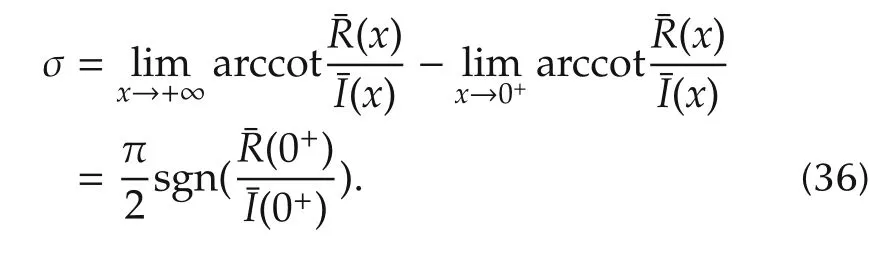
Substituting(36)and(35)into(26)yields

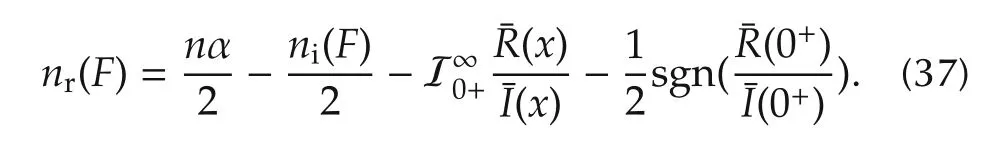
Notice that P(s)in(13)and(14)is of degree 2n-1 with the highest degree term cnsin(nπα/2)s2n-1when nα ∈Nodd.According to Lemma 3,we substitute coefficients in(14)into(11)and get

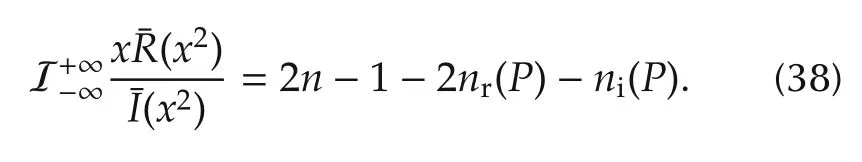
As the above step 3,equation ni(F)=ni(P)still holds as in(15).Now from the Cauchy index we have

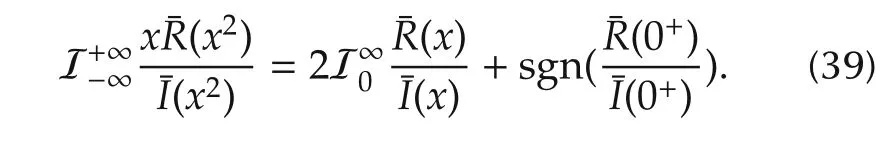
Now,from(39),(38)and(37),we have(11),i.e.,

for the case nα ∈Nodd.This completes the proof. □

Remark 2According to Theorem 1,ni(F)and nr(F)of CFDP F(s)in(12)can be obtained from ni(P)and nr(P)via the classical Routh table test on its AIDP P(s)in(13)with(14).

Remark 3Notice that the AIDP P(s)from F(s)is different from the IDP D(s)from F(s)in Lemma 1,where D(s)is commonly considered in the literature.

Remark 4Theorem 1 applies the classical Routh table test on the AIDPs for CFDPs.That is different from paper[1]where the developed Routh-type table test on the CFDPs directly.These two different approaches have their individual advantages and disadvantages respectively.The method presented here is to take the well-known classical Routh table test,that may be easy for peoples who are familiar with the classical Routh table test.

Remark 5Because the classical Routh test gives analytical(or symbolic)expressions for ni(P)and nr(P)using the coefficients of P(s),it also holds for F(s)according to(15)and(16)in Theorem 1.Such a merit is usually preferred in the analysis and synthesis of a FOS,while those methods of computing the zeros numerically may not have this merit.

Remark 6Routh test has close relation to other topics such as the zero distribution with respect to sector regions or the unit circle[19].As a result,Theorem 1 may also serve as an intermediate tool for those problems with respect to fractional order systems.

4 Examples

Example 1Consider the following CFDP function F(s)with commensurate order α=1/3 and n=4,

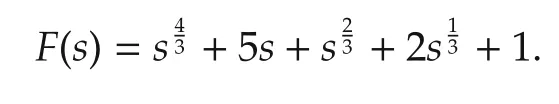
Its AIDP in(13)with(14)is

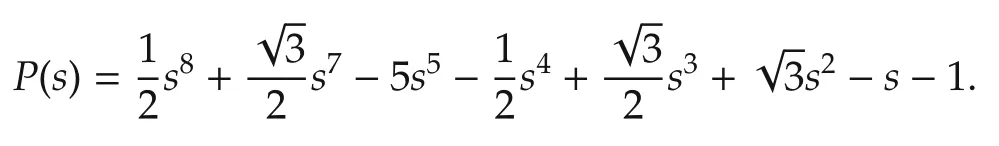
The Routh table of the P(s)is as follows as Table 2.

Table 2 Routh table for P(s)in Example 1.

Then ni(P)=0 and nr(P)=3 based on the above classical Routh table.By Theorem 1,we have

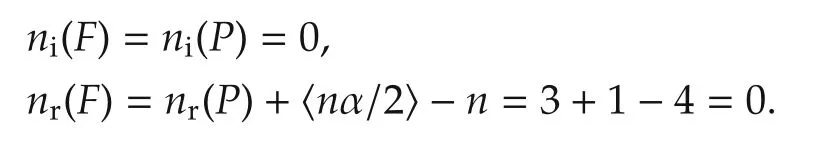
Therefore,by Criterion 1 of Lemma 1,the CFDP F(s)is stable.

and Criterion 2 of Lemma 1.Then the set of zeros of F(s)in the RPS is empty,becauseas s ∈RPS=(-π,π],is not a case here.It verifies that ni(F)=0,and nr(F)=0.

This example illustrates that Theorem 1 along with the classical Routh table test gives correct zeros distribution of F(s)without calculating its exact zeros.

For comparison,we run the method in[1],which is only available Routh-type method in the literature.It leads to a Routh-type table as Table 3.

Table 3 Routh-type table for Example 1[1].

From[1],it is noticed that the head sign change number Vf=5,the tail sign change number Vl=4,ni(F)=0(no zero row in the table),and

Thus,we have the same results from[1].Since this example has no singular case,it shows that the proposed method is easier than[1].

Example 2Consider a CFDP

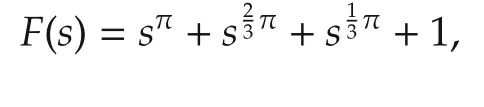
with an irrational commensurate order α=π/3 and n=3.The associated AIDP in high precision is

The Routh table of P(s)is in Table 4.

Table 4 Routh table of P(s)in Example 2.

The accurate calculation shows that the first singular case happens at row of s2,thus a small positive(or negative)number єhas to be used to replace the leading element 0.That leads to a table as above.

From the analysis on the above Routh table,we have ni(P)=0 and nr(P)=3.Thus,from Theorem 1,we have ni(F)=ni(P)=0 and nr(F)=nr(P)+〈nα/2〉-n=3+〈π/2〉-3=2.Indeed,

For comparison with[1],its Routh-type table is Table 5.

Table 5 Routh-type table for Example 2[1].

From[1],it is noticed that the head sign change number Vf=2,the tail sign change number Vl=2,no zero row with d=0,ni(F)=0,and

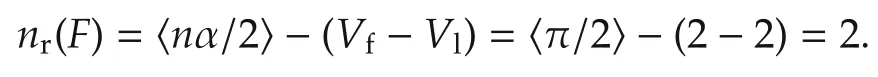
The same results are obtained.

However,it should be emphasized that row 5 has a leading 0,i.e.,a first singular case happens.It shows that the method in[1]treats the singular cases as the easiest way and with the fewest rows in the literature.

5 Conclusions

This paper presents a new method to solve zeros distribution of a commensurate fractional degree polynomial by virtue of the classical Routh test on a proposed auxiliary integer degree polynomial.

This paper discusses the stability test for the CFDPs and their fractional order systems via Routh table,which can guarantee the system behavior stable in view point of both frequency domain and state space if it passes the Routh Table test.It is noticed that Routh table test can be used broadly in science and engineering,including system behaviors,e.g.,[14-16].It will be interesting to further study the system behavior in the state space along the Routh table approach as presented here.

Furthermore,the rigorous mathematical proof is presented via the Argument principle and Cauchy index.Its significance is to present a way to apply the classical Routh table test to the commensurate fractional degree polynomials and commensurate fractional order systems for their stability analysis and synthesis.The illustrative examples show the effectiveness of the presented method.

Acknowledgements

Prof.Sheng-Guo Wang expresses his appreciation to Prof.Yong Wang at the University of Science and Technology of China for his cooperation during 2013-2016 since his Ph.D.student visited UNCC as a co-educated Ph.D.student.