Diagnosability of a class of discrete event systems based on observations

S.RESHMILA ,Devanathan RAJAGOPALAN

1.Sree Narayana Gurukulam College of Engineering,Kerala,India;2.Hindustan Institute of Technology and Science,Chennai,India

Received 22 December 2017;revised 27 December 2018;accepted 18 January 2019

Abstract The diagnosability of discrete event systems has been a topic of interest to many researchers.The diagnosability conditions for various systems have evolved based on a regularity condition that is imposed on faulty traces with respect to their observable continuations.Improving upon this weak but necessary condition,a new model of diagnosability that is based on sensor outputs,which are called observations,upon a command input is proposed in this paper.Necessary and sufficient conditions are derived for the proposed diagnosability model.The search performance of the proposed diagnosability condition is of linear complexity in terms of the power set of the system events and observations,compared to the exponential complexity of the search with the existing diagnosability regularity condition.Moreover,a system that is not diagnosable according to the existing diagnosability condition may be diagnosable in the proposed diagnosability model,which includes observations.

Keywords:Discrete event system,diagnosability,fault diagnosis,mealy automata,finite state automata

1 Introduction

The sequential behavior of a system is modeled as a discrete event system(DES)using discrete states and events.DES models can be used for fault diagnosis,but only faults that are considered in the modeling of the system can be diagnosed.However,prior to the fault diagnosis,the diagnosability of the system must be verified.

According to the literature,in the field of fault diagnosis,there are two types of diagnoses:event-based diagnosis and state-based diagnosis.Event-based diagnosis is considered in[1,2],and state-based diagnosis in[3,4].In event-based diagnosis,a fault is considered an unobservable event and is diagnosed using observable events.In state-based diagnosis,binary output vectors that are related to the system state are used to detect and isolate faults.In both methods,a diagnoser is used for the diagnosis.In event-based diagnosis,the diagnoser is initialized during the system initialization,which may cause difficulties,whereas in state-based diagnosis,it is possible to initialize the diagnoser at a later stage.

There is a large body of literature based on the diagnosability condition that was put forward by Sampath[1].However,Sampath’s condition is more of a regularity requirement than a model.It states that,a prefix trace that contains a fault and another prefix trace that does not contain the same fault cannot have identical observable suffixes.We argue that such a weak but necessary condition cannot be the basis of an efficient diagnosis technique.In this context,we propose,a command event-based sensor output as a model for diagnosis.We demonstrate that the proposed model leads to a more efficient diagnosis technique than the existing diagnosability condition.

Lamperti et al.[5]used an event-based output model that is similar to ours but more elaborate in structure.Our work differs from that of Lamperti et al.[5]in that the former emphasizes diagnosability,while the latter emphasizes the diagnosis.While diagnosis is performed via a computational approach that involves the interpretation of event sequences,diagnosability requires an automata-theoretic approach,thereby leading to an analysis of the feasibility of the diagnosis prior to the diagnosis.The diagnosability of a DES is considered in this paper.

We briefly review the existing works on diagnosability.In[6],a diagnosability condition was proposed for a system that has an uncertain sequence of observable events.In[7],the prediction of the occurrence of a fault using an asymptotically almost sure predictability(AASpredictability)for stochastic DESs was proposed,and a necessary and sufficient condition for AAS-predictability is defined.The fault diagnosis of complex communication networks was conducted using the DES approach in[8].In[9],the diagnosability of transient faults was evaluated within a bounded time interval before the fault is cleared.The diagnosability of intermittent faults based on a twin plant construction was discussed in[10],together with the diagnosability definitions for the occurrence of and recovery from faults.I-diagnosability condition[1]that involves an indicator event simplifies the diagnosability condition that was presented in[1].According to this condition,a system is said to be nondiagnosable if it is not diagnosable even after the occurrence of the indicator event.I2-diagnosability condition was defined by including an empowering event in addition to the indicator event in[11].An empowering event is an event that ensures that the indicator event will be successful in identifying the fault.

Developments in sensor networks have enabled the availability of event-based sensor outputs for fault detection upon the issuance of various commands.For example,in modern numerical relays in power system protection,sensors provide the status of each operation.After a relay has been energized,a sensor will output the status of that relay operation,namely,whether it has been executed correctly or if a fault has occurred.Our work is inspired by such new developments,and we redefine the diagnosability condition by taking advantage of the additional capability that is afforded to the system by these developments.In this paper,we propose a new diagnosability condition for a class of problems for which event-based outputs are utilized,as outlined above.Event-based outputs are associated with Mealy automata[12]in the transitions from one state to another.Although Mealy automata can be transformed to regular automata[12],we prefer to retain the former to emphasize the role of event outputs in the simplification of the diagnosability of a class of discrete event systems.

In Sampath’s approach,a diagnoser is constructed,and in the process,fault mapping is conducted using associated event and state output combinations via the inspection of the generated cycles that are involved in the fault.However,under the proposed diagnosability condition,we approach the problem of fault mapping up front in terms of observations prior to building the diagnoser and generating the cycles.In other words,we apply the diagnosability condition deeper in the domain knowledge by considering the event input and sensor output that are associated with a fault,in contrast to leaving the diagnoser building process to generate event and state output combinations that lead to fault diagnosis,as in Sampath’s case.

Moreover,a system that is not diagnosable according to Sampath’s condition may be made diagnosable according to the proposed diagnosability condition via the inclusion of observations in the system.Moreover,under the proposed diagnosability condition,the search,which is limited to faulty traces that have a specified suffix,as a special case,is of linear complexity in the system event power set,compared to an exponential complexity[1]for faulty traces that have an arbitrary suffix,as in Sampath’s case,or a polynomial complexity,as in[13].

In earlier works[14-17],the authors demonstrated,through application examples,the role of event-based outputs,which are called observations,in improving the diagnosability of systems.The present paper is an attempt at formalizing the use of observations and introducing a new diagnosability condition for a class of systems.

The main contribution of the paper is a new model of diagnosability,namely,O-diagnosability that is based on an event-triggered sensor output in a DES.The search for diagnosability verification is shown to be linear in the power set of events of the system in the proposed Odiagnosability,compared to the exponential complexity in the power set in the existing diagnosability.In addition,it is demonstrated that it is possible for a system that is not diagnosable in the existing diagnosability condition to be made O-diagnosable via the inclusion of observations.

The remainder of the paper is organized as follows:Section 2 briefly presents background on the DES and discusses the Mealy model.Section 3 introduces the proposed O-diagnosability model.Section 4 specifies the steps for building a diagnoser based on the new Odiagnosability model.A necessary and sufficient condition for O-diagnosability,together with its comparative search performance,is presented in Section 5.In Section 6,the O-diagnosability model is demonstrated on an example.The conclusions of the paper are presented in Section 7.

2 Discrete event system

2.1 Background

A DES is represented using states and events that cause transitions from one state to another state.The system is denoted by S=(X,Σ,δ,x0),where X is the set of states,Σ is the set of events,δ is the partial transition function,and x0is the initial state of the system.It is assumed that all states are accessible since we cannot diagnose inaccessible states.The set of events consists of observable events and unobservable events.The prefix closed language,namely,L(S),which is represented in short by L,is generated by the system and represents the behavior of the system.L is a subset of Σ＊,where Σ＊represents the Kleene closure of the set Σ.Σ＊is the set of all strings that are generated by concatenating elements of Σ,including the null event є.A trace is an element of Σ＊and represents a sequence of events.The prefix of an event indicates the trace prior to the event,and the suffix indicates the trace after the event.σ ∈s denotes that event σ is contained in trace s.In the proposed system model,we use observations,or sensor outputs,along with events and transitions.

2.2 System model

The system to be diagnosed is modeled as a Mealy automaton,which is denoted by G=(X,Σ,O,δe,δo,x0),where

▪X is the set of states,which includes normal states Xn and faulty states Xf,X=Xn∪Xf;

▪Σ is the set of events,which includes observable events(Σo)and unobservable events(Σuo)and satisfies Σ=Σo∪Σuo;

▪O is the set of sensor outputs;

▪The input transition function δe:X×Σ →X is a partial transition function that defines the transition from one state to the next state upon an event in Σ;

▪δo:X×Σ →O is the output transition function,which yields the output that is produced when an event in Σ acts on a state in X;and

▪x0∈X is the initial state of the system.

Typically,unobservable events are faults or events that are not recorded by sensors.Observable events are commands that are issued by controllers,and a sensor output is obtained upon the issuance of a command.Since not all command events result in sensor outputs,observable events can further be subdivided as Σo=Σs∪Σns,where Σsdenotes the set of observable command events that result in sensor outputs and Σnsdenotes the set of observable command events that do not result in sensor outputs.

Let Σf⊆Σ denote the set of events that are faults(which are referred to as faulty events henceforth)and Σf⊆Σuobecause faulty events are unobservable.The faulty events can be partitioned into disjoint groups of faults Σf=Σf1∪Σf2∪Σf3∪...∪Σfn.The states that have faults can be grouped according to the partition of the faults:Xf=Xf1∪Xf2∪Xf3∪...∪Xfn,where{Xfi},i=1,2,...,n are disjoint.

The sensor outputs can be state-based sensor outputs or event-based sensor outputs.A state-based sensor output depends on the state of the system,irrespective of the event due to which the state has been reached.An event-based sensor output is produced only upon the occurrence of an event;it indicates the successful/failed execution of the event.An event-based sensor output is called an observation henceforth.Hence,sensor outputs can be subdivided into O=Oe∪Os,where Oedenotes the set of event-based sensor outputs and Osthe set of state-based sensor outputs.oσrepresents an observation that is due to event σ,and oσ∈Oe.The set of event-based sensor outputs can be further expressed as Oe=Oen∪Oef,where Oenis the set of observations that indicate the successful(normal)operation of event e and Oefis the set of observations that indicate the failed operation of event e due to fault f.Faulty observations can be associated with unobservable faulty events.We assume that the sensors are fault-free.If sensor faults are to be considered,they must be included in the system model.

2.3 Fault observation

We model the faults and their observations as follows:

Definition 1(Mapping of faults and observations)The sensor outputs can be mapped to states by a function h,where h(state)=o if o is produced when the state is reached,irrespective of the event that caused the transition.Faults and observations are related to each other in the form of triples mij=(σfij,σi,oσi),where σfij∈Σfi,i={1,2,...,n},j={1,2,...,nfi},σi∈Σs,and oσi∈Oef,such that after any fault event σfij∈Σfi,the command event σican occur and produces observation Oσi.The number of faults in fault group Σfiis denoted by nfi,and the total number of faults in the system is

▪Mi={mi1,mi2,...,mnfi}corresponds to fault group Σfi,for i=1,2,...,n.

▪M={M1∪M2∪...∪Mn}is the set of all such triples.

To illustrate the above definition,suppose that for a pump-valve system,a pressure sensor is available that outputs a positive pressure(PP)and no pressure(NP)upon the Start pump and Stop pump commands,respectively,under normal conditions.If the pump fails,the outputs will differ,and we can map the fault“Pump failed to start”to(Start pump,NP).

Definition 2The mappings of two fault groups are equal if the(command event,observation)combination is the same for both,that is Mi=Mj,i,j ∈{1,2,...,n}iff σi=σjand oσi=oσj.

3 Diagnosability

3.1 Sampath’s diagnosability condition

Let L be the language that is generated by the system and s be a trace in the language.The empty trace is denoted by ∈.The language after s is denoted by L/s,namely,L/s={t|st ∈L}.We define ψ(σ)=sσ ∈L:σ ∈Σ,i.e.,ψ(σ)represents the set of all strings of L that end in the event σ.The projection operator P:Σ＊→is defined as in[1]:

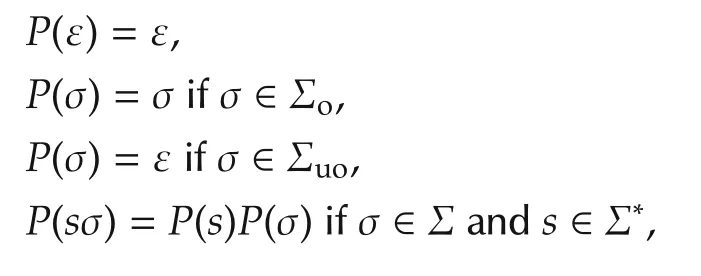
where ε represents the null string and sσ represents a language string that is generated by the system and ends in σ.Thus,projection P erases unobservable events from the event string.The inverse projection is defined as

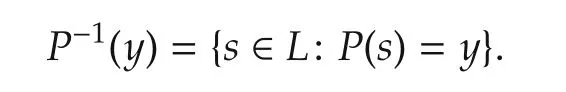
The diagnosability condition that was defined by Sampath[1]can be expressed as follows:

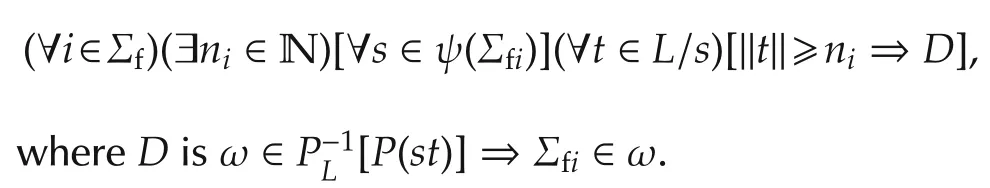
Remark 1The Sampath diagnosability condition requires that every trace that produces the same observable string as st should contain the same fault as in s.The sufficient length requirement of t ensures the uniqueness of the suffix whose preimages contain the fault.

3.2 O-diagnosability

Due to the inclusion of observations,the projection operator must be redefined as P:(Σ∪O)＊→(Σo∪O)＊.Moreover,P(σ)=σ if σ ∈Σo∪O.The other properties of P remain the same.

Definition 3(O-diagnosability condition) The Odiagnosability condition for a system requires that the following be satisfied:

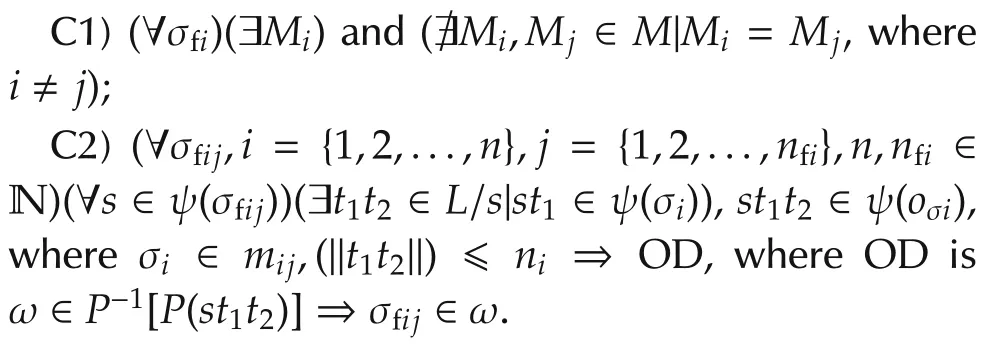
Remark 2According to condition C1,for all fault groups,there should exist a unique mapping that is not common to any other fault group.This mapping can be verified without taking into consideration the language that is generated by the system.Condition C2 is based on the language that is generated by the system.According to condition C2,the system is O-diagnosable if for all faults σfijin every group of fault events Σfi,for every string“s”that ends with fault event σfij,there exists a finite continuation(under the assumptions that unobservable strings are bounded in length[1]and of fairness in the occurrence of observable events and observations)t1t2of that string such that trace t1ends with command event σiand trace t2ends with fault observation oσi.According to the diagnosability condition,which is denoted by OD,all the prefixes of a string that end in a command event and an observation should contain the fault that is mapped to it,which is a major difference between the diagnosability conditions of Sampath[1]and O-diagnosability.In the case of Sampath,all the strings that have the same suffix should contain the same fault.Therefore,all the strings are to be searched and grouped into sets that have the same suffix without any indication of the type of suffix to be searched.In contrast,under the O-diagnosability condition,the search space for a fault is limited to the strings that contain the mapped command event and observation in the suffix.

3.3 Algorithm for verification of conditions C1 and C2 of O-diagnosability

Steps 1 and 2 for verifying condition C1 and Step 3 for condition C2:

If all faults are diagnosable,the system is diagnosable.

The mapping is evaluated in Step 1 with complexity O(n).The diagnosability is verified in Step 2,which has O(n)complexity if there are n mappings.Only if Step 2 is cleared is Step 3 performed.The worst-case complexity of Step 3 is O(n2).Therefore,the worst-case complexity of the above algorithm is O(n2),where n is the number of failure types.

4 Diagnoser

The diagnoser is an FSM that is constructed from the system model G and is used for O-diagnosability verification offline and diagnosis online.The method that is employed is a variation of Sampath’s[1]diagnoser model that considers a command input and observations. The diagnoser is denoted by GD=(Xd,Σd,O,δd,x0),where Xdis the set of states;Σdis the set of events,which satisfies Σd=Σo∪O;x0is the initial state;and δdis the transition function,which is defined as δd:Xd×Σd→Xd.The set of states in the diagnoser consists of states and labels.The set of labels is denoted by L={N}∪{F1,F2,...,Fn}∪{Ce,O},where N indicates the normal state,Ceindicates the occurrence of an event(with sensor output)and O indicates the observation state.Other labels,such as F1,F2,...,Fnindicate the fault group.The state is confirmed only via observation.

The states in the diagnoser are of the form Xd={(x1,l1),(x2,l2),(x3,l3),...,(xk,lk)},where xiis the state and liis the label.If the system G is initially normal,the initial state of the diagnoser is(x0,N).The subsequent states are determined using the transition function δd;they are the states that are reachable from x0under δd.For the state(x,l),all possible states(x′,l′)that are reachable from x are identified:where σ′∈Σoand s ∈.

Definition 4The label propagation function,which is denoted by LP,is defined as LP(x,l,sσ′)=l′.For a state x that has label l,the label changes to l′due to event sσ′.The label l′depends on s and σ′.When σ′∈Σns,l′depends on s:

When the event has a sensor output,the labels are modified to include Ce,which indicates that a command event has occurred and an observation is expected.For events that lack a sensor output,the previous comments apply.

If the label contains Ceand the event lacks a sensor output,then the labels will be changed if string s is not a null string.

When the event is an element of an observation,the label will become O,which indicates the observation state and confirms the state to be normal or faulty.

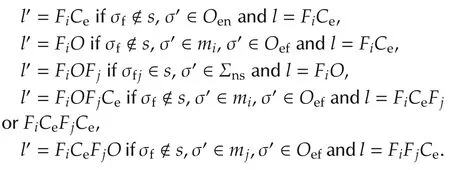
Once a fault has been labeled with O,it will remain with this label for all subsequent states.Hence,the O label with a preceding fault indicates the confirmation of its occurrence.If multiple faults occur,the confirmed fault will have the O label,and the others will not.

5 Condition for O-diagnosability

5.1 Necessary and sufficient condition

Definition 5A set of states q1,q2,...,qyforms a loop if δd(q1,σ1)=q2,δd(q2,σ2)=q3,...,δd(ql,σl)=q1and y is finite.

Definition 6A loop is called a cycle ifδd(qi,σ)=z,where i ∈{1,2...,y},σ ∉{σj}j=1,2,...,y,z ∉{qj}j=1,2,...,y.Hence,in a cycle,no event in the set of events can have a transition from a state that is in the loop to a state that is not in the loop.

To illustrate this,in Fig.1 there are two cycles,namely,A and B,and a loop,C.There will not be any branching from the cycles,whereas loops can have branches.

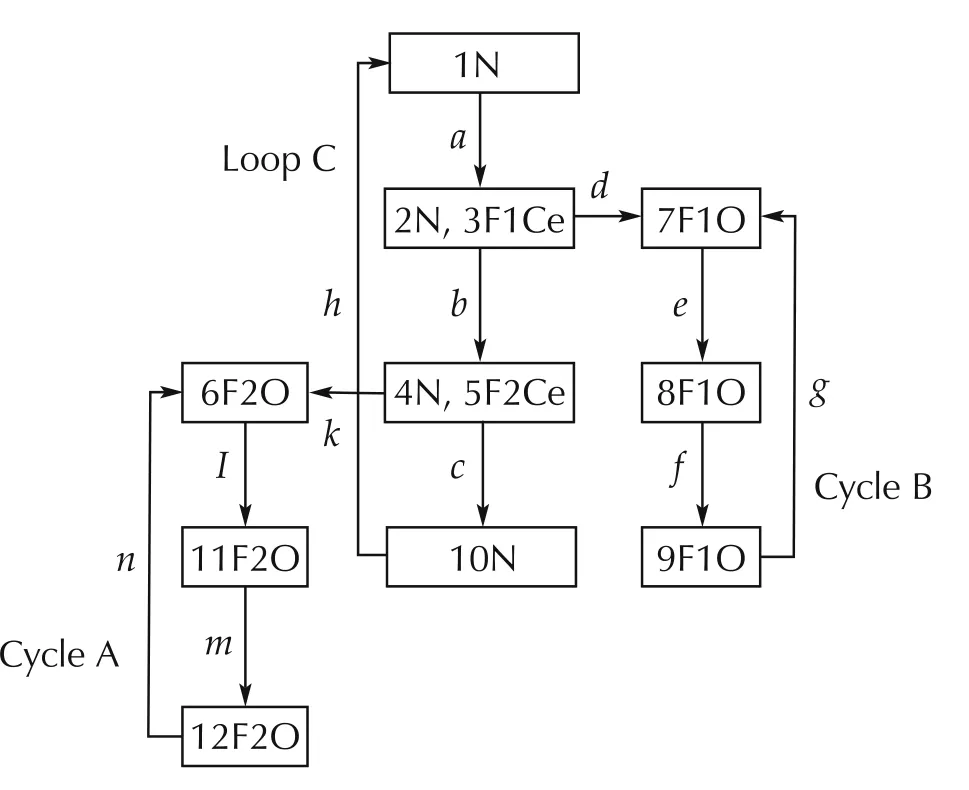
Fig.1 Sample diagnoser.

Definition 7A state qiin a diagnoser is called an observation state if δd(qi-1,oσj)=qi,where oσj ∈Oef,i.e.,qi-1can be any state in the diagnoser that transitions to qiupon the occurrence of an observation.In Fig.1,the states in cycle A are observation states and carry the label O.

Definition 8A cycle is said to be an Fiobservation cycle if it contains an observation state that has the FiO label.In Fig.1,cycle A is an observation cycle.

Definition 9A state is said to be Fiobservation uncertain if it contains labels l and l′such that FiO ∈l and FiO ∉l′.If a state has 13F2O and 12N as elements,then the state is an F2-uncertain observation,as we cannot determine whether the system is in the normal state or the F2 state.

Definition 10A state is said to be Fiobservation certain if all the labels in the state contain FiO.If a state has 13F2O and 14F2O as elements,then it is F2-certain,as we can confirm that the system is in the fault F2 state.

Definition 11A state is said to be ambiguous if it has different labels for the same state.If a state has elements 13F2O and 13N,then it is an ambiguous state.

Theorem 1A system with language L is Odiagnosable if and only if each cycle that contains Fi,i ∈1,2,3,...,n,in the diagnoser Gdis an Fiobservation cycle.

Proof(Necessity) Proceed by contradiction.Suppose that L is O-diagnosable and assume that a fault Fioccurs and there exists a cycle of states,namely,q1,q2,q3,...,qm∈Xd,where Xdis the set of states in the diagnoser,such that it is not an Fiobservation cycle.Hence,none of the states has the O label.It is possible that in the cycle,an observation never occurs in finite time.If an observation never occurs in finite time,it violates the diagnosability definition,which necessitates the presence of an observation after a faulty event in finite time,thereby resulting in a contradiction.

(Sufficiency) Assume that all the cycles that contain Fiin the diagnoser Gdare Fiobservation cycles for i ∈1,2,...,n.Let s ∈L and δ(xo,s)=x.Let t1be any string of observable events such that δ(xo,st1)=x1.In the diagnoser,q1,q2,q3,...,qm∈Xdis a cycle.By the assumption,the cycle is an observation cycle.Let(x1,l1)∈q1with Fi∈l1and Ce∈l1.This assumption can be made since the cycles are observation cycles,and each observation will be preceded by a command event.Since it is an observation cycle by assumption,there exists a string of observable events,which is denoted by t2,such that‖t1t2‖≤ni＜∞and δd(q1,t2)=q2,where(x2,l2)∈q2with Fi∈l2and O ∈l2.Assume that D is not implied;that is,∃w ∈P-1(P(st1t2))⇒σfi∉w.Hence,under the assumption of the sensors being fault-free,P(w)=P(st1t2)cannot have received a command and made observations for the i-th fault group in finite time,which contradicts the assumption of the Fiobservation cycle. □

Theorem 2Any system that is O-diagnosable satisfies the Sampath diagnosability condition.

ProofIn the O-diagnosability condition C2 of Definition 3,set t1t2=t.Sampath’s diagnosability condition follows immediately. □

Remark 3According to Theorem 2,O-diagnosable systems(including observations)are diagnosable under the Sampath condition since the latter is a regularity issue.However,it is possible for a system(without the observations included)that is not diagnosable under the Sampath condition to become O-diagnosable when observations are included.This possibility is illustrated by example in the next section.

5.2 Performance of the O-diagnosability condition

5.2.1 Comparison in terms of the search complexity

For the O-diagnosability case,letbe the power set of a string of νsymbols,which includes unobservable and observable events and observations.The complexity of the search for an O-diagnosability case will be on the order of O(Nν),since for a specified suffix that contains the command input and the corresponding observation,the condition D must be checked for all possible prefixes.However,in the Sampath case,the suffix can be any of the elements of the power set Nν.Hence,the complexity is()in the Sampath case.In terms of the power set Nνof νsymbols,the complexity of the search for O-diagnosability is linear,whereas in Sampath’s case,it is exponential.The search for the O-diagnosability condition is less complex than under Sampath’s diagnosability condition.

5.2.2 Complexity of diagnosability verification

Sampath[1]defines Xoto be the set of states in G that have an observable event.In addition,Δ is used to refer to the labels of fault types Fi:Normal and Ambiguous states.Sampath’s diagnoser has states that correspond to the power set 2X0×Δ.Jiang et al.[13]define(x,f)for characterizing the states of Go,where x ∈X1,which is the set of states in G that are reachable via observable transitions,and f belongs to the set of fault types,which is denoted by Σf.The states of Goin[13]also correspond to the power set 2X1×Σf,following Sampath[1].Jiang et al.[13]formulate a composition,namely,Go‖Go,and propose an algorithm that is claimed to have complexity,where X={x,f}.Since X1of Jiang et al.[13]and Xoof Sampath[1]are identical,|X|=|2X1×Σf|.Hence,the algorithm of Jiang et al.[13]is of polynomial complexity in the power set of states X of Goand exponential in the number of fault types.In contrast,the complexity of the proposed O-diagnosability verification method is linear in the power set of the number of alphabets,including events and observations,as discussed in Section 5.2.1 above.

5.2.3 Complexity in terms of the fault type

The complexity of the algorithm for verifying the diagnosability in terms of the fault type is exponential in O-diagnosability,as in the existing diagnosability case.However,for verification,if the diagnoser is run repeatedly for every fault type,the complexity will reduce to linear in the number of fault types.The algorithm for diagnosability verification using the diagnoser is presented in the appendix.

5.2.4 Bound on the number of events before reaching an Fi-certain observation state

The following provides a bound on the number of events that occur before a diagnosable system reaches an Fi-certain observation state.Let there be an Fiuncertain observation cycle q1,q2,q3,...,qm∈ Gd.Hence,the states in the cycle have different labels.Let us assume,without loss of generality,that N and Fiare the labels of the states in the system.When a diagnosable system is in the N state and a fault occurs,the system will not loop indefinitely in this cycle;rather,the system will reach an Fiobservation state within nievents.We can obtain a bound on nifor ∀i ∈1,2,...,n.For a fault of type i,the length of t1t2in st1t2,where s contains a fault,is bounded by ni≤n0+ci＊n0,where n0is the longest unobservable string before an observable event occurs and#Fistates in q.

6 Fluid flow examples

We consider the fluid flow example with a pump,valve and controller that was used in Sampath’s[2]paper.However,for the simplicity of the system model and the diagnoser,we assume that the pump is faultfree and the valve has faulty states.The valve has two normal states,namely,valve open(VO)and valve closed(VC),and two faulty states,namely,valve stuck closed(VSC)and valve stuck open(VSO).The pump has two normal states:pump on(PON)and pump off(POFF).The component models are illustrated in Fig.2.

The state-based sensors that are considered are a flow sensor,which outputs PF(positive flow)and NF(no flow),and a pressure sensor,which outputs PP and NP.The diagnoser in the Sampath system is illustrated in Fig.3.The system is not diagnosable,as the fault VSO and the normal states have the same trace of events.

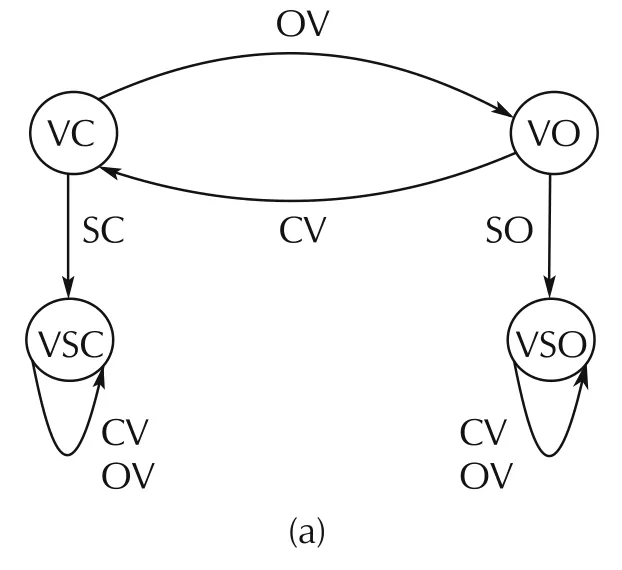
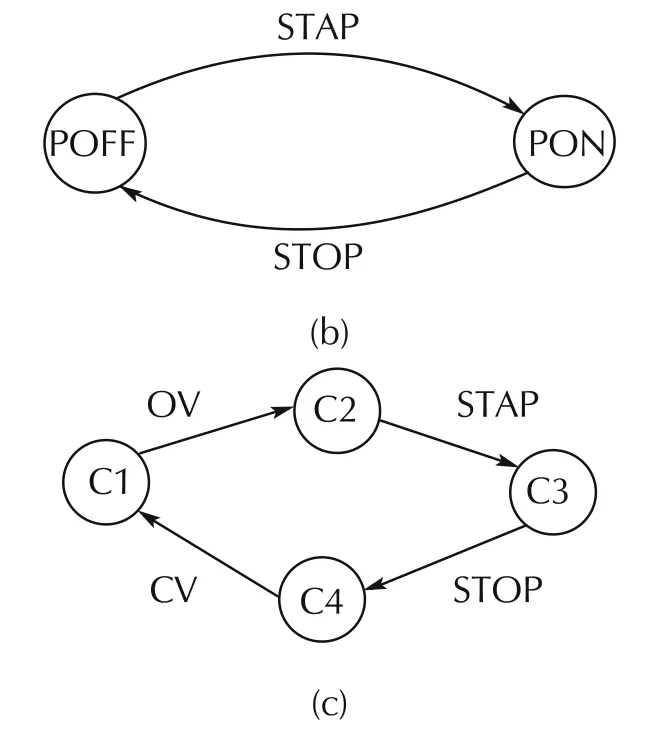
Fig.2 Component models of a valve,pump and controller.

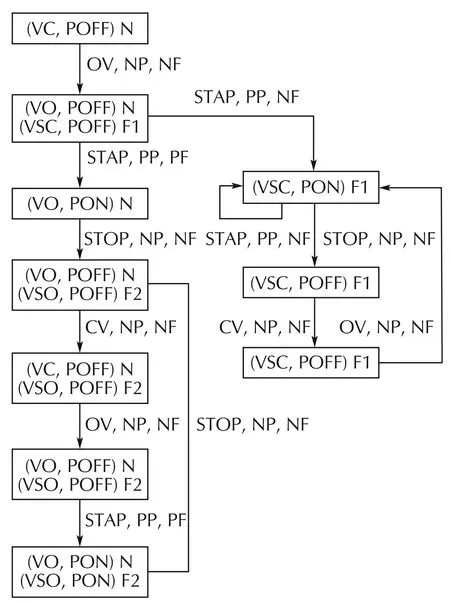
Fig.3 Diagnoser.

In some cases,event-based sensors are available to indicate the status of valve operations.Such systems can be modeled using the proposed system.Suppose the system has valve sensors that indicate when the output valve is opened(VIO),when the valve is not opened(VNO),when the valve is closed(VIC)and when the valve is not closed(VNC).The model of the components is illustrated in Fig.4.In the proposed system,the diagnosability is verified using conditions C1 and C2.To check condition C1,faults are mapped with events/observations,as listed in Table 1.

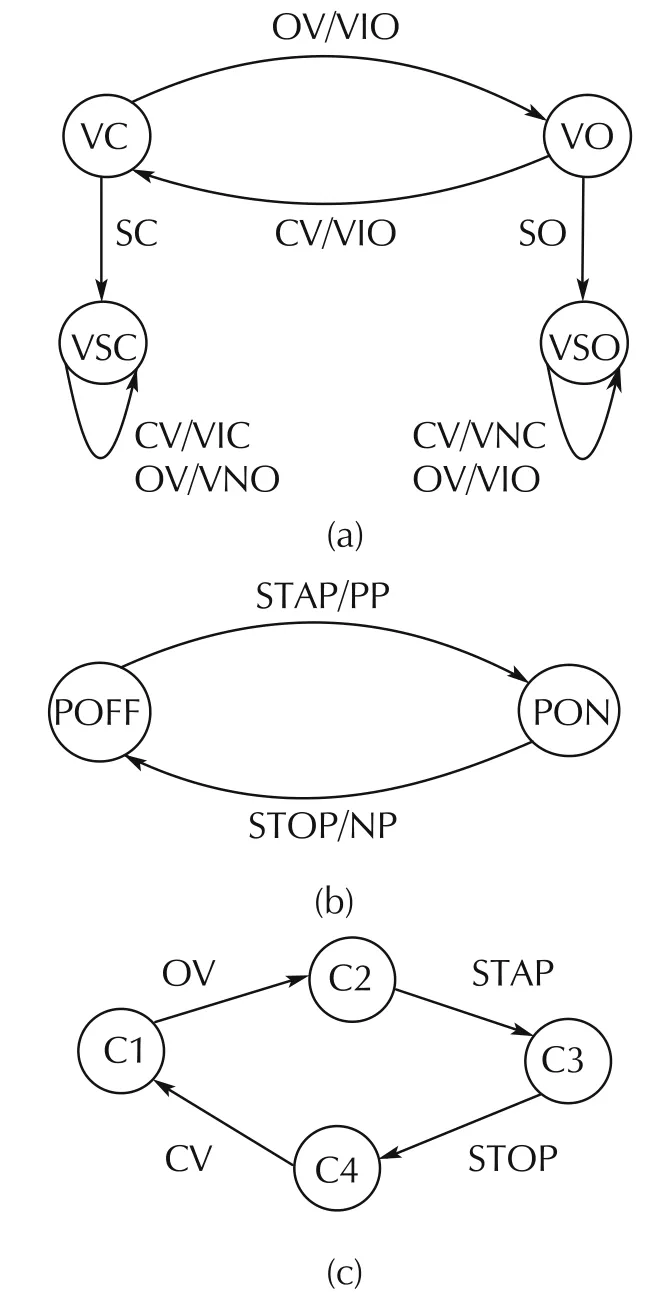
Fig.4 Component models with observations.

Table 1 Mapping of faults and events/observations.

Faults VSC and VSO are mapped;hence,they satisfy condition C1.We can check condition C2 to confirm the diagnosability.There will be many strings of events in the system.Of these strings,only one will be of normal operation;all others will contain faults.To diagnose a fault,the prefixes of all strings need not be checked.Only the prefixes of strings that contain a mapped event/observation must be checked for the presence of a fault.Therefore,to check,for example,whether VSC is O-diagnosable,we must check whether the prefix of each string that contains OV/VNO contains fault VSC.Similarly,for VSO,we must check the prefixes of strings that contain CV/VNC.OV/VNO is present in all the strings that contain fault VSC,and CV/VNC is present in all the strings that contain fault VSO.Hence,the system satisfies condition C2.The diagnoser is illustrated in Fig.5.

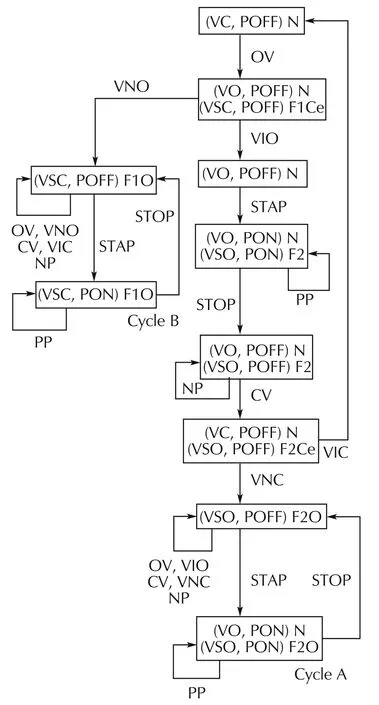
Fig.5 Diagnoser in the proposed system.

The cycles A and B are observation cycles that confirm the O-diagnosability of the system.

7 Conclusions

A new diagnosability condition(which is called Odiagnosability)of a DES model that is based on eventbased outputs(which are called observations)for diagnosis is proposed in this paper.A diagnoser is defined based on the proposed O-diagnosability condition.A necessary and sufficient condition for a system to be Odiagnosable is derived.The search for O-diagnosability verification,being a special case,is shown to be linear in the power set of all the events in the system,compared to exponential complexity in the power set in the case of the existing diagnosability.In addition,an upper bound on the number of events that occur before a diagnosable system satisfies the O-diagnosability condition is presented.A system that is not diagnosable according to the existing diagnosability condition may become O-diagnosable with the inclusion of observations.

The presence of observations that correspond to faults upon a command event opens up the possibility of the direct observation of faults at the component level without having to deduce the faults based on a combination of event and sensor outputs in various components by employing a synchronous composition of component FSMs.We plan to extend the system diagnosability to component-level diagnosability using event-based observations in our future work.

Appendix

Algorithm for diagnosability verification using the diagnoser

Step 1Compute diagnoser Gdas follows:

1)Define the set of labels as L={N}∪{F1,F2,...,Fn}∪{Ce,O}.

2)Define the initial state with label N.

3)Identify the subsequent states that are reachable from x0using the transition function δd.

4)Find the labels of the subsequent states using the label propagation function,namely,LP.

Step 2Verify the diagnosability of the system:

1)Identify the Ficycles in Gd.

3)Check whether l=O and Fi=Fjin all the states in the cycles.

a)If true,the system is diagnosable.

b)If false,the system is not diagnosable.