明确分类标准 依序分而治之*——例谈固定一个顶点的等腰三角形分类问题

●郭源源

(金陵中学西善分校,江苏 南京 210005)

在数学中，当问题所给对象不能进行统一研究时，就要根据对象本质属性的相同点和不同点，将研究对象分为不同种类，然后逐一研究，汇总结论，这种解决问题的方法称为分类讨论[1]．分类讨论思想的运用，往往能使复杂问题条理化、繁琐问题简单化，是培养学生思维严谨性和缜密性的关键，同时也是提升学生问题探究能力的重要方式．在初中数学中，分类讨论占有很高的地位，它既是一种重要的数学思想，也是一种常见的数学逻辑方法．

几何中等腰三角形的分类，因其图形的直观性和其边角特征的常用性，成为了经典分类问题，也是历届中考的热点问题之一．其中固定两个顶点的等腰三角形分类问题通过以两个顶点为圆心、线段长为半径分别作圆，并连出垂直平分线，从而利用3个轨迹即可有条理地解决这种分类问题，即“两圆一线法”.但固定一个顶点的等腰三角形分类问题，无法用这种方法解决，需要学生具有较强的分类意识和读图构图能力，笔者结合自己在教学中的实践所得，以近些年的中考题和其变式为例，谈谈这类问题的解法策略，与同仁交流、分享．

1 以“顶角顶点”和“腰的位置”分类

例1 在一张长为7、宽为5的矩形纸片上，现要剪下一个腰长为4的等腰三角形(要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上)，则剪下的等腰三角形的面积为______．

(2015年内蒙古自治区通辽市数学中考试题第16题)

分析 本题对于剪下的等腰三角形，不明确的点有两处：其一是与矩形顶点重合的是等腰三角形的顶角顶点还是底角顶点，因此需要分类讨论，分类标准可以按顶角顶点来分;其二是长为4的腰具体位置并不清楚，需要根据图中的数据分析可能的位置，因此也需要分类．故本题用二级分类可有条理、不重不漏地解决．

解 1)当重合顶点A为等腰三角形的顶角顶点时，等腰三角形的构法如图1所示，则

图1 图2 图3

2)当重合顶点A为等腰三角形的底角顶点时，因为4小于矩形的两条边长，所以一条腰只能在矩形的边上，可分为边AD和边AB两类：

①长为4的腰在边AD上，构法如图2所示，则

②长为4的腰在边AB上，构法如图3所示，则

例2 在一张长为16、宽为8的矩形纸片上，现要剪下一个腰长为9的等腰三角形(要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上)，则这样不同形状的等腰三角形有______种．

分析 本题基于例1的分类标准，将腰长改为9，因为腰长介于矩形的长和宽之间，所以矩形重合顶点的这条腰的位置可能在边上也可能在矩形内部，这样画出的等腰三角形就会更多.故更加合理的分类标准是有条不紊地画出所有图形．

图4 图5 图6

解 1)当重合顶点A为等腰三角形的顶角顶点时，等腰三角形构法如图4所示，△AEF为所求.

2)当重合顶点A为等腰三角形的底角顶点时，因为9介于矩形的长和宽之间，所以AE这条腰可能在矩形的边上，也可能矩形的内部：①若腰AE在边AD上，等腰三角形构法如图5所示，则△AEF,△AEF′,△AEF″为所求；②若腰AE在矩形内部，等腰三角形构法如图6所示，则△AEF,△AEF′为所求．

综上所述，画出的等腰三角形有6种，形状不同的有4种．

点评 等腰三角形的分类是老生常谈的话题，但等腰的二级分类一直是学生解题中的难点.此类题型注重思想方法的掌握，突出考查学生的思维水平、想象和推理能力、数据分析能力．因涉及的结果较多，图形的构法较活，且基于不同经验下学生的分类标准可能不同，这就造成了此类题解法过程混乱、没有条理，最终容易出现漏解或重解的情况．笔者认为解决此类题，切不可一上来就陷入一个个具体图形中，不要急于关注结果有几个，而应从大局出发思考结果有几类，明确分类标准，再分而治之．

2 以“顶角顶点”和“腰底大小”分类

例3 在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形(要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3).

(2015年江苏省南京市数学中考试题第25题)

图7

分析 本题的等腰三角形，不明确的点仍有两处：其一，顶点A是等腰三角形的顶角顶点还是底角顶点？其二，长为3的边是等腰三角形的腰还是底？基于这样的条件分析，确定分类策略是以“顶角顶点”和“腰底大小”为标准的二级分类，如图7所示．

解 1)当A为等腰三角形顶角的顶点时：

①若3为腰，小于正方形边长4，故长为3的腰只能在正方形边上，如图8所示；

②若3为底，由正方形的对称性，知3为底的图有两种，如图9所示．

2)当A为等腰三角形底角的顶点时：

①若3为腰，小于正方形边长4，故AE这条腰只能在正方形的边上，如图10所示；

②若3为底，由数据分析知AE这条底只能在正方形的边上，如图11所示．

综上所述，画出大小不同的等腰三角形有5种．

图8 图9 图10 图11

例4 在边长为4的正方形ABCD中，以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为4.1的所有大小不同的等腰三角形有______种．

分析 本题在延续上述二级分类标准的前提下，将等腰三角形的边长改为4.1，因其大于正方形的边长，故长为4.1的边不管为底还是为腰，都必须在正方形的内部，这样就会有更多的结果，分类构图如图12～图15所示，共画出7种大小不同的等腰三角形．

图12 图13 图14 图15

点评 在明确分类标准、依序分而治之的策略下，解题过程呈现条理化和层次化，从而突显出思维的结构框架．这种方法的渗透，不仅仅是在教学生如何解题，更重要的是教会学生如何思考．此题在掌握了分类策略后还可以继续往下研究，所给边长在什么范围内等腰三角形有5种？什么范围内有6种？结果可能有8种吗？等等．

3 以“腰底大小”和“腰底位置”分类

例5 在边长为8的等边△ABC中，以A为一个底角顶点，另外两个顶点在等边△ABC的边上，且含边长为7的所有大小不同的等腰三角形有______种．

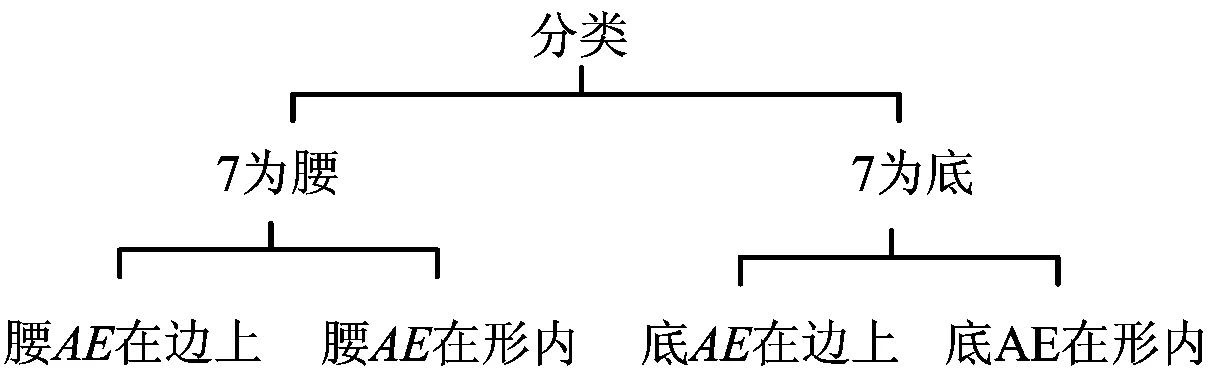
图16

解 1)当7为腰时：①若腰AE在边上，则等腰三角形构法如图17所示，△AEF,△AEF′为所求；②若腰AE在形内，如图18所示，无法构出符合要求的图．

2)当7为底时：①若底AE在边上，则等腰三角形的构法如图19所示，△AEF为所求；②若底AE在形内，则等腰三角形构法如图20所示，△AEF,△AEF′为所求．

综上所述，画出的等腰三角形有5种，大小不同的有4种．

点评 本题将基本的载体图形由正方形变成了等边三角形，因图形性质的不同，就会造成所给数据边的位置分析不同．当AE的长介于等边三角形的高和边长之间，会有两种可能位置.针对这一现象，还可以将本题中的A为一个底角顶点改编为A为一个顶角顶点，那么结果就更多了.但不管怎么变，此类题的解题策略始终是先高位思考，明确分类的标准，再依序分而治之，化整为零，各个击破，最后汇总归纳．这种化繁为简的思维恰恰是数学的魅力所在．

综上，固定一个端点的等腰三角形分类构图问题看似虽小，没有繁琐的计算和复杂的推理，但其实质却蕴含着丰富的数学知识和思想方法，整个过程涉及到分类策略的运用、数据条件的分析、图形位置的推理、识图构图的方法等，思维含量很高，对提升学生思维的严谨性和全面性有很大的帮助．

学生分类思想的形成，不仅来源于教师教学时的方法渗透，还来源于学生解题时的回顾反思.一种思想方法的掌握绝不是一朝一夕的事，而是平时教学和解题中不断沉淀、逐步完善的一个漫长过程．根据几轮教学的实践，笔者认为对于初中学生分类思想的培养大致需经历以下4个层次：

1)培养学生的分类意识．很多分类讨论的题目，学生的错误不是因为解错，而是因为漏解，压根就没想到还有别的情形．故解题教学时要紧抓审题环节，并不是解完题再想有无别的可能，而是审题中对“模糊条件”和“分类信号词”的捕捉，让学生在审题环节就能意识到这是一道分类题.

2)引导学生制定分类的标准．意识到分类就不会漏解了吗？如本文中的分类，若没有清晰的分类标准，解全答案并非易事，因此一个合理的分类标准至关重要．教学时，最合理的分类标准不是教师直接告知的，而是学生由各种标准之间对比产生的.基于学生理解，思路最清晰，结构最简单，就是好标准.

3)指引学生破解各类情形．通过分类标准，将一道题分解成具有并列关系的几个子问题，然后依序分而治之．这类子问题的解法，往往方法和思路如出一辙，只要学生解题有序，会解一个，就能通解一类.

4)带领学生回顾分类的过程．波利亚解题四步骤中最后一个步骤是回顾反思，它是提炼方法和感悟思想最好的时机．没有经历回顾反思的题只是一道题而已，有了回顾反思“一道”就能变成“一类”，解题就能从“无限”的题走向“有限”的思想方法[2]．

最后，分类讨论作为一种重要的数学思想和数学方法，它的渗透和运用需要一定的意识习惯和经验积累，而意识和经验的积累都必须在解题实践中获得，只有在实践中锤炼的思想方法才是学生真正能留得住、带得走的数学财富．