直觉与逻辑并行 推理与运算共进*——两道质检题引发的思考

●郑 良

(灵璧第一中学，安徽 灵璧 234200)

1 问题提出

安徽省宿州市高二年级上学期期末考试如期进行，其中理科第21题与第22题是学生得分的分水岭.全年级学生的平均得分分别为3.03分与2.21分，均低于第1)小题的分值(满分为4分).笔者对此思考：除了试题的位置(整卷的最后两道题)与答题时间紧张等客观因素外，学生在答题中还暴露出哪些问题，其根源是什么，如何应对…….

2 案例剖析

例1 如图1，在直角梯形ABCD中，AD∥BC，AB⊥BC，BD⊥CD．将△ABD沿BD折起，折起后点A的位置为点P，得到几何体P-BCD(如图2所示)，且平面PBD⊥平面BCD.

1)证明：PB⊥平面PCD.

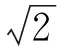
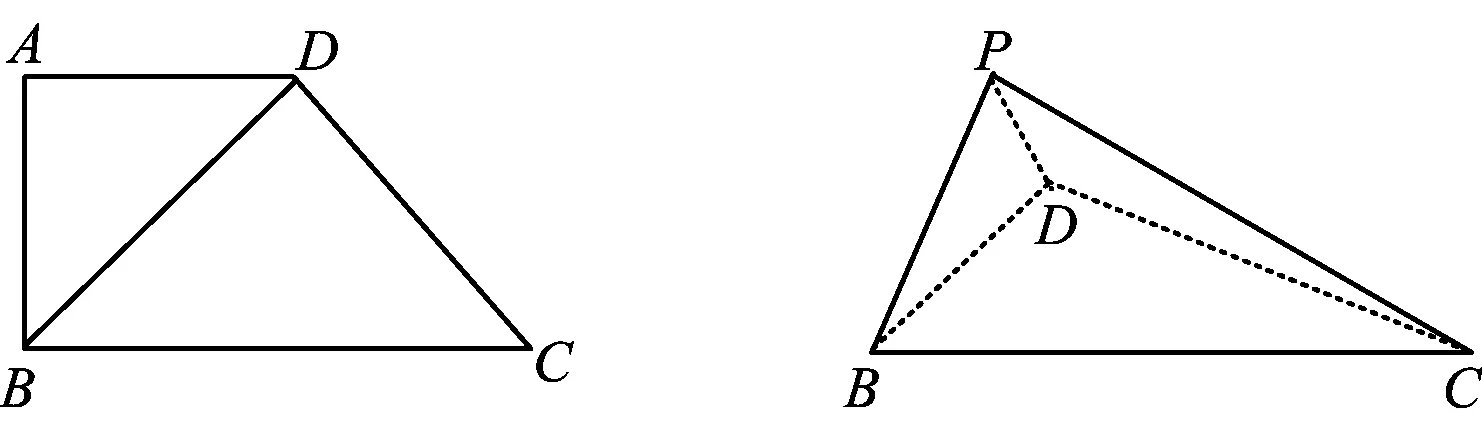
图1 图2

(安徽省宿州市13所重点中学2018学年第一学期高二期末质量检测数学理科试题第21题)

命题组给出第2)小题的参考答案如下：

2)解法1 由第1)小题知CD⊥平面PBD，即∠CPD为直线PC和平面PBD所成角，则

得

又△ABD∽△DCB，从而

故AB=2.

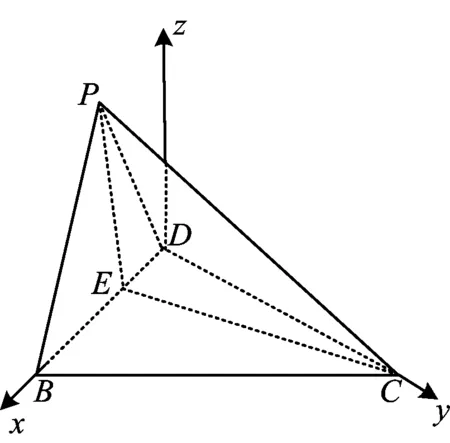
图3

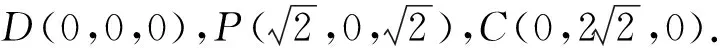
设平面PDC的法向量为n1=(x1,y1,z1)，则

取n1=(1,0,-1);设平面PCE的法向量为n2=(x2,y2,z2),则

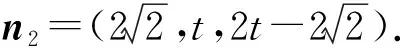
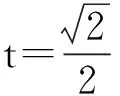
本题以图形的折叠为背景，考查空间中直线与平面垂直的判定和性质定理、平面与平面垂直的性质、空间中直线与平面所成角、二面角的平面角等知识，考查学生的空间想象能力、运算求解能力以及数学运算、直观想象和数学建模等数学素养.

对于第1)小题，学生的主要错误有：

1)符号滥用.数学是一门语言，它拥有特定的符号及符号之间的关系、词汇、文法与句法等.如少数学生满篇把“平面”简写成“平”，把线面关系连接符号“⊆”写成“∈”.根源在于学生没有准确理解(直线与平面均为空间的点的集合)集合间的关系.

2)丢三落四.运用判定定理或性质定理时丢三落四,导致无法推出正确的结论.如学生“由BD⊥CD直接得到CD⊥PB”或“由PB⊥PD直接推出PB⊥平面PCD”等，学生识记不准源于教学缺乏结论的探究过程和必要的正反例思辨，学生不理解问题的来龙去脉，只能断章取义.

3)无中生有.不少学生添加条件“AB=AD”强行建立空间直角坐标系，表明学生空间想象能力弱，综合法认识不到位，只有“华山一条路”.先证后用是解题的基本规范，也是演绎推理的根基.

4)作茧自缚.部分学生在平面PBD内作PF⊥BD后利用“平面PBD⊥平面BCD”关系，无异于放弃高速公路不走，修建羊肠小道蜿蜒前行，说明学生视野狭窄，审题能力有待提高.

对于第2)小题，学生的主要错误有：

1)蒙混过关.从求解目标知需要求出AB或BD的长度(两者相互依存)，多数学生尝试将点P置于z轴(在平面PBD内过点P作PO⊥BD于点O，以O为原点、OB，OP所在直线分别为x轴、z轴建立空间直角坐标系)上，必须先确定AB的长度；若以命题组提供的答案的方式建立空间直角坐标系，可先建系再求AB的长度.多数学生没有正确解读条件而无法求出AB的长度，直接使用“AB=2”或用“由平面几何知识易得AB=2”来敷衍(在访谈中得以确认)，这与数学严谨、求实的科学态度相悖.如何确定AB的长度(即刻画BD⊥CD)？由题设知∠BAD=∠BDC=90°，∠ADB=∠DBC，这恰是“△ABD∽△DCB”的判定条件，水到渠成.

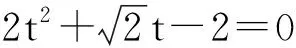
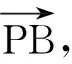
4)思维无序.学生思维无序，表述混乱;部分学生用综合法求解，总体得分不高.表明学生“立体几何平面化”的化归与转化思想和(两次)有序“隔离”的方法仍有待提高.

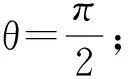
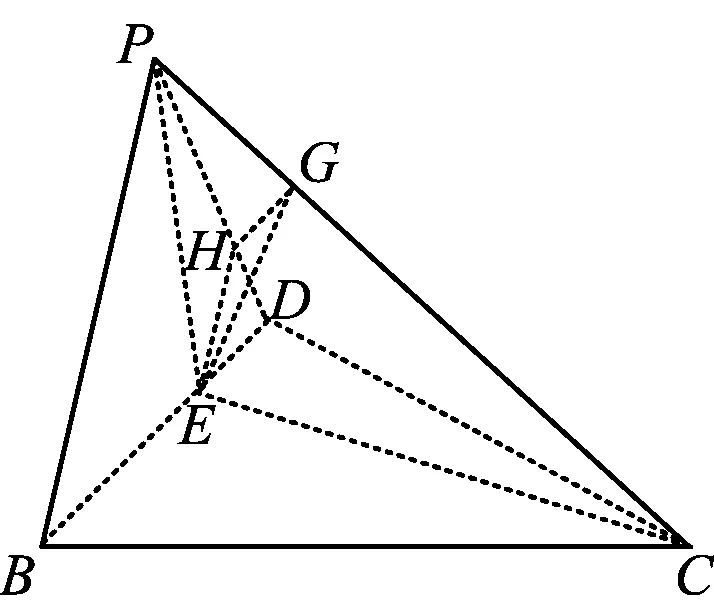
图4

2)解法2 如图4，在平面PBD内，过点E作EH∥BP交PD于点H，则EH⊥平面PDC，且EH=DH=2λ，从而PH=2-2λ.在Rt△PDC中，过点H作HG⊥PC于点G，联结EG，由三垂线定理可知∠EGH即为二面角D-PC-E的平面角.由△PHG∽△PDC，得

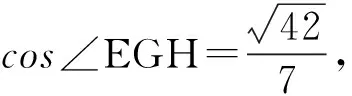
我第一次把我家后山和语文课本联系起来是在我读了杜牧的《山行》之后。我家就在岳麓山下，诗人写的爱晚亭我也去过，但我看到的却没有他写的这么美。自此以后，我常在学习之余爬山，或在阳光明媚的清晨，或在夕阳西下的傍晚，春夏秋冬，随兴而至，百看不厌。

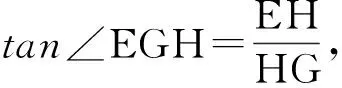
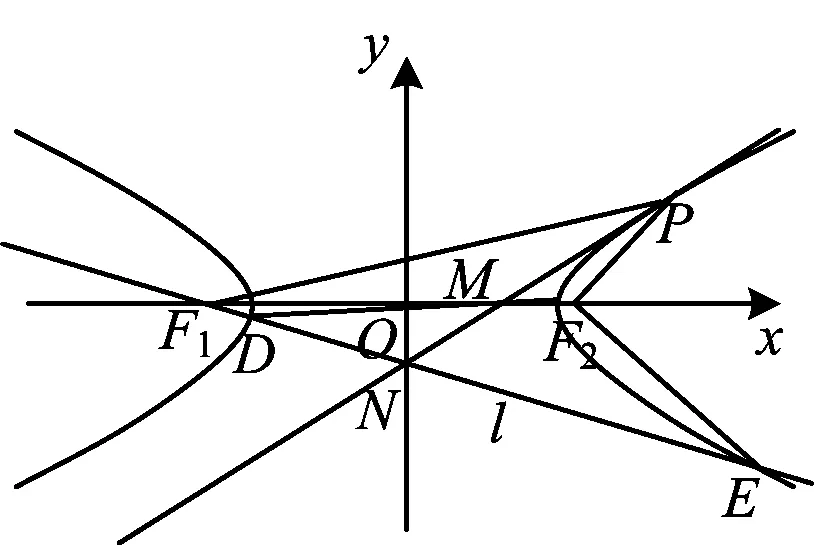
图5

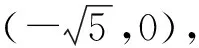
1)求双曲线C的标准方程；

2)求△F2DE面积的最大值.

(安徽省宿州市13所重点中学2018学年第一学期高二期末质量检测数学理科试题第22题)

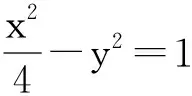
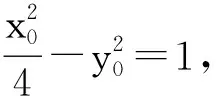
由点M(m,0)在∠F1PF2的平分线上，得

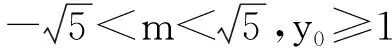
从而

于是

即

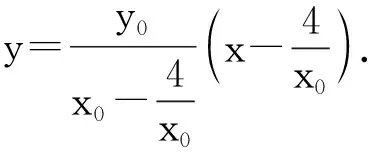
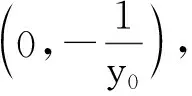
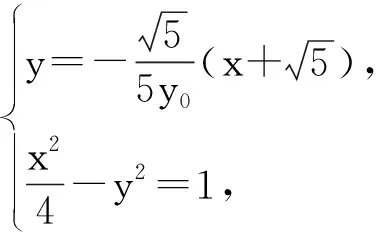
其判别式大于0.设D(x1,y1)，E(x2,y2)，则

因此

因为y0≥1，所以

y1+y2<0，y1y2>0，

得

y1<0,y2<0，

从而S△F2DE=S△F1F2E-S△F1F2D=

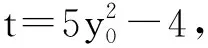
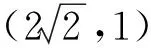
本题以直线与双曲线的位置关系为背景，考查双曲线的标准方程、直线与双曲线的位置关系、韦达定理、弦长公式及二次函数的性质等知识，考查化归与转化思想和运算求解能力以及数学运算、数学抽象和数学建模等数学素养.

对于第1)小题，学生的主要错误有：.

1)张冠李戴.误用椭圆的定义或性质求解双曲线的标准方程.

2)计算错误.利用定义法(正向运算)的学生基本无误，而用待定系数法(逆向解方程组)的学生运算错误率较高.

3)功亏一篑.正确求出a，b，c后，总结时把双曲线的标准方程写成椭圆的方程.

对于第2)小题，学生的主要错误有：

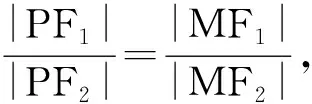
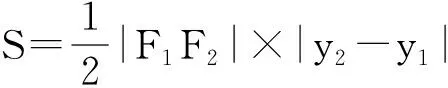
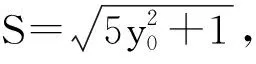
3 教学思考

3.1 立足教材，适度拓展

教材是教师教学与学生学习的最重要的载体.历次考试表明：试题越接近教材，学生考得越差.例1第1)小题推理证明的依据及第2)小题建系的标准在教材中交代得清清楚楚，第2)小题求角的计算公式在教材中讲得明明白白；例2中圆锥曲线的第一定义在教材中反复强化，通过具体案例抽象概括出圆锥曲线的第二定义(并在教材中用极坐标方程进行深化).教材是参天大树的根，教学要避免一叶障目就要正本清源，抓住主干不放松.如三角形的内角平分线定理作为正弦定理的重要应用理应及时渗透，并及时链接平面几何法等证明方法；又如直角三角形的射影定理在“基本不等式”中有所提及，教师要及时跟进并补充其应用.

学生不重视教材由来已久，主要原因是其所遇试题(表面形式上)与教材“相距甚远”；多数教师思想上重视教材，却没有有效的行动落实.近年来，学案与教辅严重侵占学生的时间与空间.教师追求量而不核对质，粗线条管理无法早期发现学生的错误并及时矫正.教师应该研习并挖掘教材，通过对高质量的交送作业(不少教师不以教材为蓝本布置交送作业，而用教辅取而代之)和试卷的面批面改将学生处于萌芽状态的错误及时遏制；对教材中的阅读、探究、课题等栏目要合理定位，力争探究到位；对学生的疑惑进行寻根之旅，揭开千变万化形式下相对稳定的本质，切实感受到教材的力量.教师要对教材有敬畏之心、虔诚的学习态度，通过教材引领师生的行为规范.

3.2 强化直观,逻辑跟进

数学是研究数量关系和空间形式的一门科学.如何获取解题思路？固然离不开解题经验，更需要感性与直观的素材，它是合情推理的切入点.教学过程中发现很多学生过于聚焦目标而不善于探寻直观的构件.如处理几何问题时没有画图的意识和能力，探寻规律问题时没有通过具体特例归纳结论的习惯等.数学家希尔伯特认为：不管在哪个领域，公理化方法都是并且始终是一个合适的、不可缺少的助手.借助直观想象获得解决问题的方向，通过逻辑分析推进或调整解题方案，合理组织论证，用规范性语言将看似零乱的、互不相关的知识，组成一个条理清晰的整体.在例1中，学生的逻辑混乱、思维不清晰、表达不连贯，表明学生对立体几何的掌握不够完善.

3.3 展示过程,精准落实

反思基础教育课程改革，基础性研究做得不够,学生认识问题是从具体到一般，我们在教学中却往往是先给出一般的东西，然后用具体的东西来阐述这个一般的东西，包括教学的呈现和教材的呈现.这些问题应该进行长期的研究[1].教学中不少教师分析解题思路、抄录解题的关键步骤，使得基础薄弱的学生跟不上教学节奏，导致学生对教学可远观而不能近玩.纸上得来终觉浅，绝知此事要躬行，教师要先独立解题，感知学生可能存在的问题，然后结合学生的解题情况稚化自己的思维，示以学生思维之道.如在例1中，教师可让学生说出对第1)小题预期的证明过程，对第2)小题求AB长度的切入点及确定点E位置的推进过程；又如在例2中，确定角平分线PN的方法、表达S的方式等，教师对学生提供的各种方案进行分析，展示心路过程，让学生看得见、想得清、学得来.

3.4 全局视角,一线串通

数学是一个统一的整体，数学学习则要分阶段稳步推进.苏霍姆林斯基曾说：教师在关于教材的思考上使用的精力越少，则学生的脑力劳动的效率越高.如果教师把全副注意力都用在自己关于教材的思考上，那么学生感知所教的东西就很费力，甚至听不懂教师的讲述.因此，教师所知道的东西，就应当比他在课堂上要讲的东西多10倍，多20倍，以便能够应付自如地掌握教材，到了课堂上，能从大量的事实中挑选出最重要的来讲……一个好的教师，并不见得能明察秋毫地预见到他的课将如何发展，但是他能够根据课堂本身所提示的学生的思维逻辑和规律性来选择那唯一必要的路径而走下去[2].

学生记忆的消退、认知的递进性与教材的模块化等特点决定了教学要循序渐进.教师只有站在学科教学的制高点，才能对教学作长期规划与合理布局，教学时才能相机而动.内容理解肤浅，则教学不见本质，索然无味、不解其惑；反之，内容过难则会曲高和寡，学生力不从心，无所适从，自然无法让知识从容生长.教师要基于学情，因材施教.数学核心素养既相互独立、又互相交融，是一个有机的整体，它需要学生对问题及时而持续地反思，进而构建整体结构，理解蕴含于其中的思想方法，进而不断地领悟并内化为数学素养.如推理与运算相互渗透，彼此交融，良好的数形结合能力就是直觉与逻辑齐头并进的体现.又如例1与例2分别为立体几何、平面解析几何问题，但终究为几何问题.学生只有掌握了平面几何的基础知识，才能对立体几何、平面解析几何问题进行恰当的处理，才能实现对几何问题的融会贯通.