课堂因“意外”而精彩*——记一次染色问题探究的奇幻之旅

●盛耀建

(湖州中学,浙江 湖州 313000)

在课堂教学中，往往会出现一些意外，它是超出教师课前教案设计而出现的新情况、新问题，它具有动态性，是稍纵即逝的.如果我们能准确、及时地捕捉到这些生成性资源并加以合理利用，将使课堂不断涌现精彩、鲜活的画卷.

笔者在最近一次主题为“多面体顶点染色问题”的知识拓展类选修课的课堂教学中，学生解答中出现的多种意外，使得笔者在解决意外的过程中，带领学生经历了一次探究之旅，收到了意想不到的效果.

1 部分课堂实录

例1 如图1，从5种颜色中选出3种颜色，染在四棱锥S-ABCD的5个顶点上，每个顶点上染一种颜色，并使同一条棱上的两端点异色，求不同的染色方法种数.

作为一个范例，笔者先让学生思考若干分钟时间，然后与学生一起总结出该题的一种有效染色方案：分步乘法计数原理.具体分析如下：

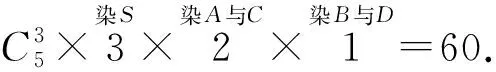
变式1 从5种颜色中选出4种颜色，染在四棱锥S-ABCD的5个顶点上，每个顶点上染一种颜色，并使同一条棱上的两端点异色，求不同的染色方法种数.

1.1 几种答案产生

变式1以学生自主思考为主，教师引导为辅，进行合作探究.

师：从题意分析可知，选出的4种颜色必须要染完.有没有同学能依据例1的解决方法，设计一种合理的染色方案.

(思考片刻后，教师请学生代表发言.)

(360种不是笔者想要的答案，“课堂意外”开始萌芽.)

师：生1的答案是360种，其他同学有不同意见吗？

生2：生1的答案不对，应该是300种！

师：你是怎么想的？

生2：生1的方法包含了点A与点C同色且点B与点D同色的情况，而此时仅用了3种颜色，不符题意，故需除去这种情况.而例1告诉我们仅用3种颜色的染法有60种，因此变式1中不同的染色方法种数仅需在生1回答的360的基础上减去60即可，应为300.

(300种也不是正确答案，“课堂意外”得到蔓延.)

师：好像有点道理，还有不同意见吗？

坐在角落的生3欲言又止，笔者观察到了，请其回答.

生3：我跟前两位同学的答案都不一样，我算出来只有240种(笔者脸上露出一丝笑容).我是这么想的：共5个点仅4种颜色，从图形结构分析可知，分点A与点C同色(点B与点D不同色)有

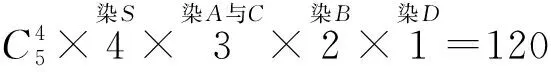
或点B与点D同色(点A与点C不同色)有

故不同的染色方法种数为120+120=240.

(一道题竟然得出了3种答案，“课堂意外”达到顶峰.)

顿时，班级里像是炸开了锅，笔者顺势将学生以前后桌4人为单位分成若干组进行讨论，到底哪个答案正确？

几分钟后，从小组统计结果显示，绝大多数小组认为240种是正确答案.

师：很好，240种是正确答案.生3的做法中注意到了有5个点却仅4种颜色，故必有两个顶点同色，从点A与点C同色(点B与点D不同色)和点B与点D同色(点A与点C不同色)两个角度进行分类，得出不同的染色方法种数为120+120=240(称其为法1).

1.2 错误原因分析

师：生1的答案“360种”明显是错的，那么生2为什么也错了，问题在哪里？

(纠错，找出错解原因，将探究活动推向高潮.)

生4(自言自语)：仅用3种颜色的染法有60种是对的，因此360种肯定不是用3种或4种颜色染色的染法种数，这里一定有问题！我们可以先求出用3种或4种颜色染色的染法种数！

笔者借用生4的话给全班学生作了些许引导，不一会儿生5用间接法求得：

师：生5采用间接法求得用3种或4种颜色染色的染法种数果然是300，因此用生2的想法做此题应该是300-60=240.

师：生1的做法能否通过改进得出正确答案呢？

笔者话音未落，生1举手了.

全班顿时响起了热烈的掌声！

1.3 问题本质揭示

为什么生2不能将生1得到的360种作为用3种或4种颜色染色的染法种数？

为了能够说明问题，揭示问题本质，笔者在课堂上又举了两例：

例2 现有4种颜色，染在四棱锥S-ABCD的5个顶点上，每个顶点上染一种颜色，并使同一条棱上的两端点异色，求不同的染色方法种数.

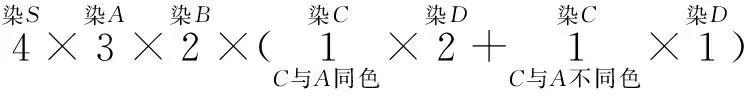
例3 现有5种颜色，染在四棱锥S-ABCD的5个顶点上，每个顶点上染一种颜色，并使同一条棱上的两端点异色，求不同的染色方法种数.

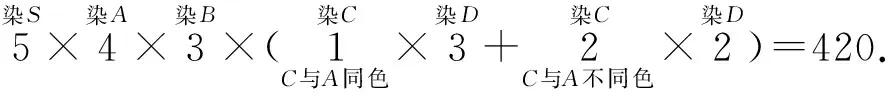
犯了杂揉(一方面要求4种颜色都要用，另一方面将仅用3种颜色的染色的情况也考虑进去了)的错误.

修正错误后可得：

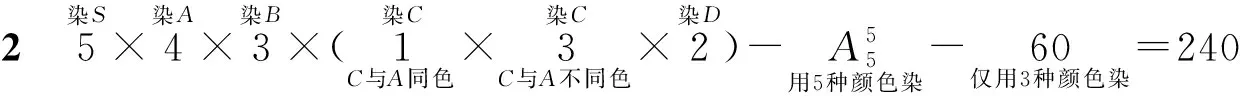
2 课后反思

2.1 课堂意外的认识

课堂意外是一种非常宝贵的课中生成性资源，是教学的瑰宝，值得每一位执教者珍惜，处理得当会使原本平淡的课堂大放异彩，处理不得当也会使精彩的课堂走向平庸.课堂教学作为一个“活”的过程，千变万化，谁也无法阻止“意外”的发生.前苏联教育家苏霍姆林斯基说过：“教育的技巧并不在于能预见到课堂的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉中作出相应的变动.”

2.2 错误资源的利用

课堂中实时产生的错误也是一种教学资源，教师可以利用学生的认知结构引导学生发现错误，带领学生探讨错误产生的原因，并归纳总结，以防再次犯错.整个过程中，学生在不断地完善自身知识结构的同时，也在对比、感悟、思辨、总结中享受成功的喜悦，这也加强了师生间、生生间的互动互助，激发了学生的积极性，培养了学生思维的严谨性，最终达到提高教学效率和育人的目的.正如美国心理学家贝恩布所说：“差错人皆有之，作为教师不利用是不可原谅的.没有大量错误作为台阶就不能攀登上正确结果的宝座.”[1]

2.3 面对意外的处置

课堂意外在所难免，作为教师面对意外应有正确的心态，要认识到课堂教学是服务于学生的.当学生有意无意地跳出教师设计的思路时，千万不能不知所措，也不能硬着头皮按原计划上课.教师应冷静对待，充分调动自己的知识经验和机智，及时调整教学思路，把课堂意外转化为“教学资源”，使意外成为课堂教学中“无法预约的精彩”.俄国教育家乌申斯基说：“不论教育者怎样地研究理论，如果他没有教育机智，他就不可能成为一个优秀的教育实践者.”在本节课的实施过程中，课堂意外随3种答案的依次出现被一步步推向顶峰，面对课堂中出现的一波波“意外”，笔者并没有自乱阵脚，而是做到了“让学生把话说完”，并以问题的形式顺势将“意外”抛出引导学生将其推向顶峰，最终利用纠错环节，将“意外”一网打尽.