紧急避障工况下的分布式驱动电动汽车稳定性控制＊

张缓缓 李庆望 彭博 高超 严帅

（上海工程技术大学，上海 201620）

主题词：分布式驱动 电动汽车 转矩分配 车辆稳定性 PID控制 线性二次型调节器

1 前言

分布式驱动电动汽车相比于传统内燃机车辆以及中央电机驱动车辆，省去了发动机、离合器、变速器等一系列部件，结构更为简单。由于每个车轮上都装有轮毂电机，对于各轮的转矩操纵更为精确、方便，是电动汽车发展的重要方向之一[1-2]。近年来，许多学者对通过控制各驱动轮上的转矩来提高整车的稳定性进行了研究[3-8]。Teng G等[4]考虑轮胎在极限状况下的非线性特性并据此设计了轮胎侧偏刚度估计器来实时计算轮胎的侧偏刚度，在此基础上设计了自适应控制算法来提高极限工况下车辆的稳定性。Zhai L等[6]针对轮毂电机驱动电动汽车提出了一种电子稳定控制算法，该算法利用电机的驱动力和制动力分配控制来提高车辆的稳定性。

在极限工况下保持车辆稳定对普通驾驶员而言是非常困难的，因为在达到或超过轮胎与路面的附着极限时，车辆横摆运动对转向盘转角输入的响应迅速降低，驾驶员的转向操纵很难影响车辆的横摆运动，原有线性区的驾驶经验无法帮助驾驶员“有预见性”地操纵，过度的转向或制动操作反而恶化了车辆的稳定性状态[9]。

在车速较高时，紧急避障工况会使汽车迅速进入非线性区域[10]，仅凭驾驶员的操作无法使车辆重新回到稳定状态，本文利用分布式驱动电动汽车的自身优势，通过对各驱动轮转矩的优化分配，利用对准稳定工况的动力学控制来阻止车辆进入不可控的非稳定状况。

2 控制策略设计

2.1 转矩分配的控制逻辑

车辆高速行驶并突然转向时会导致横摆角速度过大而引起车辆失稳，通过将驾驶员实际输入的油门踏板信号和转向盘信号与理想的线性二自由度模型进行比较，从而计算所需的附加横摆力矩，并将此力矩合理地分配给各轮上的轮毂电机和制动器，从而矫正过大的横摆力矩使车辆保持稳定状态。

当车辆处于急转弯工况时，由于在极短时间内输入较大转向盘转角，横摆角速度过大，容易出现过度转向而产生侧滑，继而出现失稳的状况。前外轮和后内轮对车辆横摆稳定性的影响一般大于其他两轮[11]，对于过度转向状态的车辆，可采用内侧车轮增矩和外侧车轮减矩甚至制动的策略对车辆进行稳定性控制。

因此，本文控制策略分为两个阶段：当车辆的横摆角速度过大而失稳时，减少外侧车轮电机的转矩，此为第一阶段；如外侧车轮减少转矩后仍不能保证车辆的稳定性，即经过相同的失稳判断之后，外侧车轮的转矩减少为0后仍不能满足要求，对车辆的外侧车轮实施制动，同时对内侧车轮实施增矩，此为第二阶段。控制流程如图1所示。

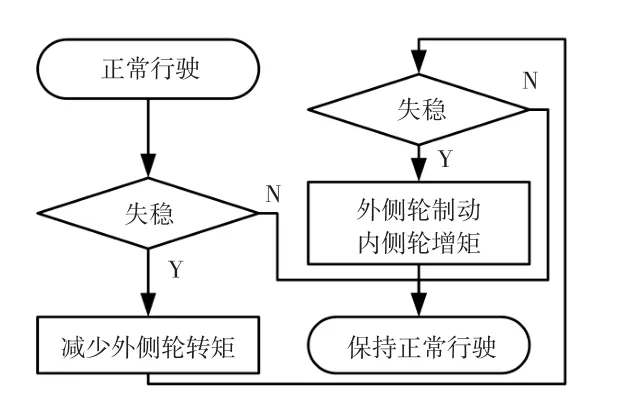
图1 控制策略流程

2.2 转矩分配的控制结构

所设计的控制结构如图2所示，由驱动力矩控制器、执行器和整车模型组成。驱动力矩控制器分为上层控制器和下层控制器。上层控制器根据车辆输入的状态，计算出所需的附加横摆力矩，并将其传递给下层控制器；下层控制器根据各约束条件，将附加横摆力矩合理分配给执行器。图2中，Vd和V分别为车辆的目标速度和实际速度；ωd和ω分别为车辆的理想横摆角速度和实际横摆角速度；βd和β分别为车辆的理想质心侧偏角和实际质心侧偏角；δf为前轮转角。

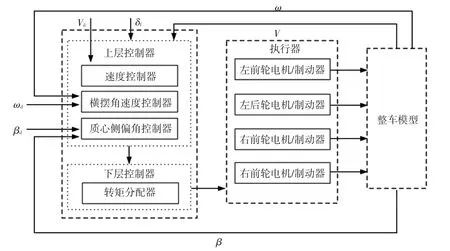
图2 转矩分配控制结构

3 分布式驱动电动汽车模型和轮胎模型

3.1 7自由度车辆模型

在汽车转向稳定性研究中，主要考虑车辆的纵向运动、侧向运动以及横摆运动。因此，采用7自由度非线性车辆模型进行仿真分析，如图3所示，包括汽车的纵向、侧向、侧倾运动，以及4个车轮的转动，不考虑车辆的俯仰、侧向、垂向运动。

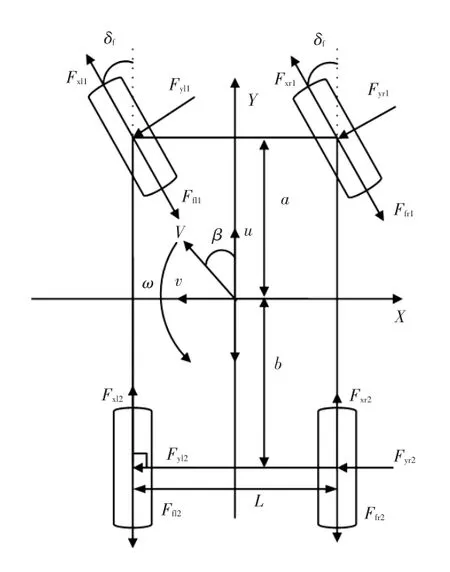
图3 整车模型

该车辆模型沿X轴方向和Y轴方向以及绕Z轴的动力学方程分别为：

式中，FX、FY分别为沿X轴和Y轴方向的合力；m为车辆质量；v为车辆横向速度；u为车辆纵向速度；MZ为绕Z轴的横摆力矩；IZ为车辆绕Z轴的转动惯量。

式（2）、式（3）可以详细表示为：

式中，a、b分别为车辆质心到前、后轴的距离；L为前、后轮距；Fxl1、Fxr1、Fxl2、Fxr2分别为左前轮、右前轮、左后轮、右后轮所受的纵向力；Fyl1、Fyr1、Fyl2、Fyr2分别为左前轮、右前轮、左后轮、右后轮所受的横向力；Ffl1、Ffr1、Ffl2、Ffr2分别为左前轮、右前轮、左后轮、右后轮所受的滚动阻力。

3.2 轮胎模型

选用CarSim自带的“魔术公式”轮胎模型，该模型可以表达出轮胎的各向力学特性，统一性强，其形式为：

式中，y为纵向力、侧向力或回正力矩；x为轮胎侧偏角或纵向滑移率；D为峰值因子；C为形状因子；B为刚度因子；E为曲率因子。

4 控制器设计

4.1 速度控制器

根据文献[12]所提供的速度控制器可知，车辆所需总转矩Td与车辆前轮转角δf、目标车速Vd以及实际车速V有关。速度控制器选用PID控制方法来计算输出转矩，控制器的偏差量为目标车速和实际车速之差，PID控制器的输出量为车辆所需的总转矩，其控制原理如图4所示。

图4 速度控制器原理

偏差定义为：

经过PID控制器的输出总力矩为：

式中，Kp为比例系数；ti为积分时间常数；td为微分时间常数。

当δf＞0时，采取协调分配方式，将总的转矩协调分配给各车轮上的电机；当δf=0时，采取平均分配方式，每个车轮上分得的电机转矩为Td/4。另外，由于是匀速行驶，Vd和V的差距很小，此时Td也很小。

4.2 横摆力矩控制器

参考文献[13]中线性二自由度模型，如图5所示，根据该模型可以写出二自由度模型的状态方程：

式中，K1和K2分别为前、后轮的侧偏刚度。

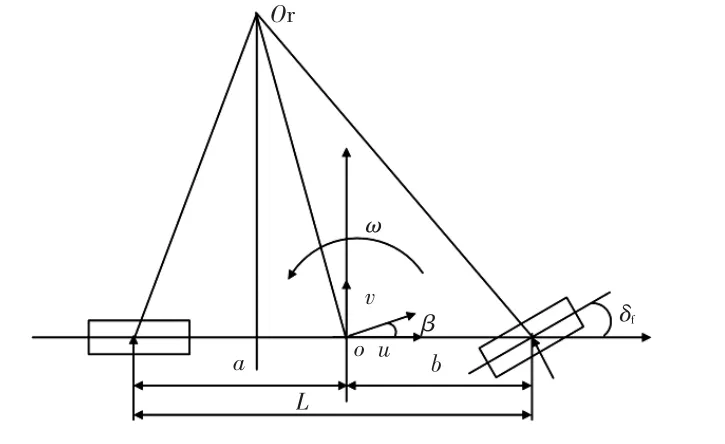
图5 线性二自由度模型

本文基于线性二次型控制算法理论[14]，引入最优控制指标，其性能泛函为：

式中，u(t)为系统输入，取任意值；x（t）为误差矢量；Q1为正定对称矩阵；Q2为正定或半正定矩阵。

最优控制就是要找到合适的系统输入u*(t)使得性能泛函J最小，u*(t)可以表示为：

式中，P为Riccati方程的解，Riccati方程为：

在横摆角速度控制器中，前轮转角作为系统的输入，理想横摆角速度ωd和理想质心侧偏角βd作为系统的状态变量，根据式（9）可得：

当实际质心侧偏角超过设定值或实际的横摆角速度与理想横摆角速度相差过大时，车辆会失稳，此时，施加反向附加横摆力矩ΔM，使车辆回到稳定状态，车辆的运动方程为：

式中，B1=[0 1/IZ]T。

将式（14）减去式（13）可得：

但是在地面附着极限下，车辆的侧向加速度ay受到如下约束：

式中，μ为路面附着系数；g为重力加速度。

当侧偏角较小时，忽略其影响，ay可以表示为：

结合式（16）和（17），可以得到修正后的理想横摆角速度：

取理想质心侧偏角βd=0。

4.3 转矩分配器

转矩分配器的作用是在满足稳定性的前提下将车辆的广义力合理地分配给各执行器。对分布式驱动电动汽车而言，各执行器的分力即轮毂电机/制动器施加给各车轮的纵向力。

4.3.1 转矩分配第一阶段

以左转工况为例，根据前文提到的转矩分配的两个阶段，可以得出车辆达到期望状态所需的附加横摆力矩ΔM和第一阶段所能提供的附加横摆力矩ΔM1：

如果车辆在转矩分配的第一阶段能够稳定，则ΔM=ΔM1。由于匀速阶段每个车轮上的转矩相同，故Fxr1=Fxr2。同时，考虑到节能因素，该阶段对内侧轮不作控制，最终可得每个车轮上的纵向力以及所需的力矩：

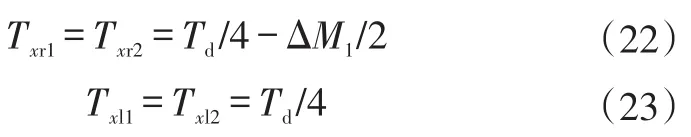
4.3.2 转矩分配第二阶段

在第一阶段中，当外侧车轮转矩减少为0时，可以提供该阶段最大的附加横摆力矩ΔM1max：

然而，如果实际横摆角速度过大，第一阶段所提供的ΔM1max也不能满足稳定性要求，第二阶段采取对内侧轮增矩，对外侧轮制动的控制策略，所需的横摆力矩为：

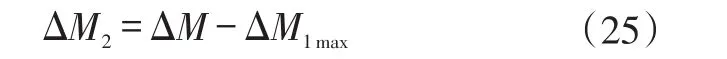
该阶段主要考虑的是对内侧轮转矩及外侧轮制动力矩的分配，以所有车轮负荷率的平方和最小作为最小优化目标，提高稳定裕度，防止单个车轮增加的转矩过大而打滑或施加的制动力矩过大而抱死。目标函数的表达式为：

式中，Cl1、Cl2、Cr1、Cr2为权重系数；Fzl1、Fzr1、Fzr1、Fzr2为各轮上的垂向载荷。

优化分配过程中车辆所需的纵向力和横摆力矩为：

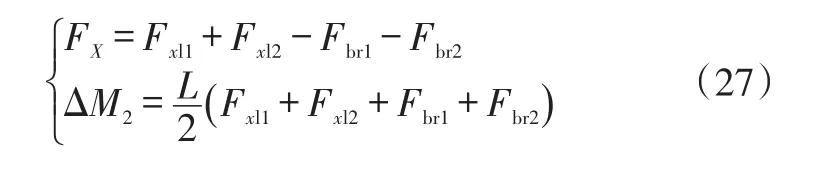
式中，Fbr1、Fbr2分别为右前轮和右后轮制动力。

电机转矩和地面附着力对车轮的限制为：

式中，Tmax为电机峰值转矩；R为滚动半径。

根据文献[15]结论所知，式（26）中Cl1=Cr1=1，Cl2=Cr2=2。综合式（26）、式（27），得到新的目标函数，然后分别对Fxl2、Fbr2求偏导。

在满足式（28）的条件下，最终的解为：

根据式（27）、式（29）、式（30），第二阶段各轮上的最终转矩分别为：

5 仿真与分析

利用CarSim与MATLAB/Simulink平台搭建了整车动力学模型，同时采用双移线工况和蛇行工况模拟紧急避障工况，仿真时间为60 s，为模拟极限工况，取地面附着系数为0.2，相当于压实的雪地路面。具体的仿真车辆参数如表1所示。

表1 仿真车辆几何参数

5.1 双移线工况

仿真车辆原地起步，加速到60 km/h之后以双移线工况行驶。仿真针对无控制情况与采取转矩分配方式的有控制情况进行对比研究。仿真结果如图6所示。

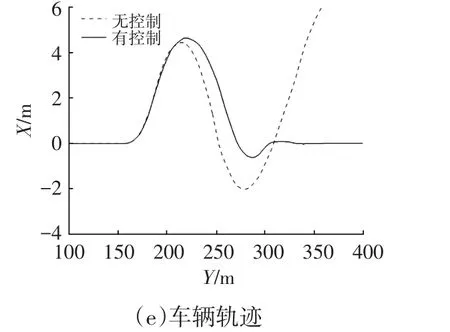
图6 双移线工况仿真结果

由图6可知：在无控制情况下，车速变化较大，横摆角速度急剧增大，车辆的行驶轨迹偏差较大，车辆失稳侧滑；采用转矩分配控制时，速度波动范围很小，横摆角速度在正常范围内波动，在变道结束后，横摆角速度趋于0，质心侧偏角始终处于0°附近，各轮的转矩波动较小并趋于平稳。仿真结果说明，本文提出的控制策略能保证车辆的动力性，使车辆处于稳定状态并有效地控制车辆按照期望路线行驶。

5.2 蛇行工况

车辆原地起步并做匀加速直线运动，当速度达到36 km/h时进行蛇行运动，仿真结果如图7所示。

由图7可知：有控制时的车速波动较无控制时小，波动程度最大不超过1 km/h，对整车的动力性影响相对较小，对能量损耗的减少起到一定的作用；当车辆处于不稳定状况时，横摆角速度和质心侧偏角都在理想范围内波动，但是无控制的曲线相对于有控制的曲线存在一定的滞后，这是由于此时车辆的轮胎力均已达到饱和状态，为了保持车辆稳定而牺牲了轨迹跟踪；在有控制时，出现了转矩为0的状况，而此时对应的制动轮缸压力不为0，说明在该控制方法下，制动系统发挥了作用，但是由于制动系统的参与，一定程度上降低了车速。相比较于仅利用制动力得到期望横摆力矩的普通ESP控制方法，本文的控制方法在满足稳定性的同时，综合驱动力与制动力得到期望横摆力矩，减少制动力对动力性的影响。

由仿真结果可以看出，在双移线工况和蛇行工况下，车辆在无控制的情况下均出现失稳，在转矩分配控制下可以保持一定的稳定性。

图7 蛇行工况仿真结果

6 结束语

本文对紧急避障工况下分布式驱动电动汽车稳定性系统进行了分层优化，分别基于PID控制和LQR理论对速度控制器和横摆角速度控制器进行了优化，对横摆力矩进行了精确计算，设计了协调转矩控制的下层转矩分配控制器，仿真结果表明，该系统提高了车辆的稳定性。

相对于简单的转矩分配控制，利用转矩的协调控制，减少制动力在主动安全控制中的参与范围，起到了减少能量损耗的作用。