四轮独立驱动电动汽车多模式自适应车速估计方法＊

孙磊 刘平 杨明亮 罗立全 陈晓菲

（1.西南交通大学，机械工程学院，成都 610031；2.西南交通大学，先进驱动节能技术教育部工程研究中心，成都 610031）

主题词：四轮驱动 电动汽车 车速估计 联合仿真 硬件在环

1 前言

相对于传统驱动形式的车辆，分布式驱动汽车（如双驱动桥式四轮驱动、轮边驱动、轮毂驱动等车型）因其每个车轮均可成为驱动轮，在行驶过程中都可能发生较严重的滑移或者滑转，所以通过传统的基于非驱动轮轮速计算车速的方法会出现误差较大的情况。车速信息是车辆行驶过程中的重要状态参数，因此，高精度车速估计对于四轮独立驱动电动汽车有着极为重要的意义。

对于四轮独立驱动汽车的车速估计，国内外学者进行了大量相关研究。吴利军[1]等人以两轮驱动轿车为研究对象，提出了一种基于加速度及轮速信息的参考车速估计方法，引入了非驱动轮滑移率，但对于四轮驱动汽车，其适用性有限。齐志权[2]等人通过基于最小轮速的卡尔曼滤波递归算法估算配备驱动防滑（Acceleration Slip Regulation，ASR）系统的四轮驱动汽车车速，但该算法在制动情况下并不适用。Te Chen[3]等人对四轮独立驱动电动汽车的纵向力、侧向速度以及横摆角速度进行了分析和估算。李臻[4]提出了一种基于非线性动力学模型的扩展卡尔曼滤波算法的统一车速估计方法，该方法在转向盘转角较大时估计误差较大，全工况适用性较差。阳贵兵[5]等人提出了一种参数自适应卡尔曼滤波算法的车速估计方法，但通过加速度计算车速时未考虑车辆侧向及横摆运动对车速的影响。余卓平[6]等人基于分布式驱动电动汽车，提出了一种纵向车速非线性自适应估计算法，基于加速度计算车速，但加速度信号受干扰严重，准确的实时信号较难获取。万钢[7]等人根据轮速传感器测得的轮速、电机实际输出力矩以及车轮垂直载荷计算出各车轮的利用附着系数，再利用附着系数和各车轮轮速差异估算各车轮的滑移率，从而估算车速，该方法需要实时计算车轮的垂直载荷，增加了结果的不确定性。袁景明[8]、褚文博[9]、罗禹贡[10]提出的车速估计方法中都均基于轮加速度对车轮稳定性进行判断，但是在工况复杂的情况下，轮加速度与车辆质心加速度相关性变差，导致判断不准确。

从现有研究及应用的情况来看，分布式独立驱动汽车的车速估计方法较为多样，实现难易程度、成本、可靠性、准确性也各有优缺点，能够兼顾多种技术要求的方案较少。本文基于轮速、车辆纵向加速度等信号提出了一种多模式自适应车速估计方法。

2 车速估计算法

本文所研究的车速估计算法按照模块化设计思想通过Simulink搭建功能模块，先采集轮速、加速度等信号，再对每个车轮进行稳定性判定，并根据4个车轮的稳定性状态自动选择相应的车速估计方法，最后经滤波处理得到估计的车辆纵向速度。其中车轮稳定性基于等效车辆纵向加速度（即通过轮加速度折算到车辆质心处的加速度）进行判断，目的在于更加准确地实时评估每个车轮的稳定性状态。该车速估计方法的总体结构如图1所示。

图1 车速估计方法结构示意

2.1 基于轮速的等效车辆纵向加速度估计

对于准确判断某个车轮的滑移/滑转情况，比较理想的方法是在每个车轮轮心处加装速度或加速度传感器，并结合轮速信号计算相应的滑移/滑转率。显然，受技术和成本限制无法采用这种方法，因此，本文提出一种基于轮速分析的等效车辆纵向加速度判断方法。在假设车轮纯滚动的前提下通过对轮速信号的微分处理获取车轮的纵向加速度并通过6自由度车辆动力学模型折算到车辆质心处，得到等效车辆纵向加速度，再通过与安装在质心处的加速度传感器所采集的实际加速度信号进行对比，从而对车轮稳定性进行判断，由于等效加速度在假设车轮纯滚动的情况下计算获得，同时考虑了转向和横摆运动的影响，可以较准确地反映无滑移/滑转的情况下车辆的纵向加速度。

考虑车轮加速度、车辆纵向加速度，车辆侧向加速度的6自由度车辆模型如图2所示。

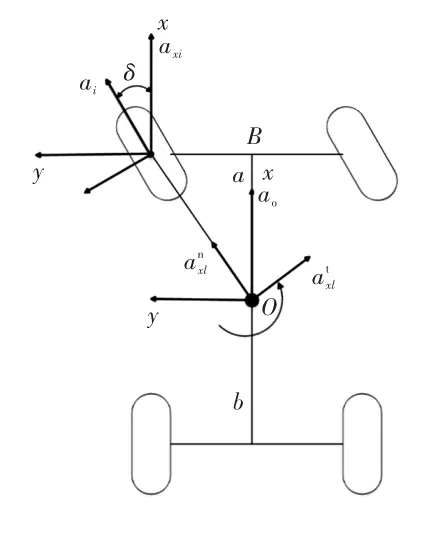
图2 6自由度车辆模型

车轮转动角加速度为：

式中，n为车轮转速。

车轮的切向加速度为：

式中，r为车轮有效滚动半径；i=1,2,3,4分别代表左前、右前、左后、右后4个车轮。

式（2）中，车轮有效滚动半径为车辆半载时的车轮静态半径，由于车轮的动态滚动半径较难获取，在传统车速计算方法中忽略了该值的动态变化，同时，本文车速估计方法主要针对轿车或非载重型商用车，胎压及载荷变化较小，车轮滚动半径在行驶过程中的变化量不大，因此同样忽略车轮滚动半径动态变化对车速估计的影响。

忽略车轮侧向运动的影响，由于车轮在轮胎平面内近似做刚体平面运动，且假设与路面发生纯滚动，则车轮切向加速度即为轮心加速度，即：

车轮切向加速度在车辆纵向上的分量为：

式中，δ为车轮转角。

考虑到车辆在转向过程中横摆运动对车辆侧向运动的影响，已知轮心加速度、横摆角速度，由基点法可得车辆质心处的纵向加速度分量为：

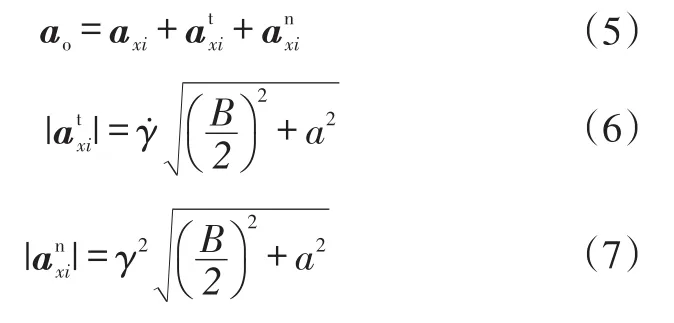
式中，ao为车辆质心处等效纵向加速度；γ为横摆角速度；分别为车辆质心相对于轮心的切向、法向加速度；B为轮距；a为质心到前轴的距离（若通过后轮计算则换为质心到后轮的距离b）。

由式（5）～式（7）可得车辆质心处的纵向加速度为：

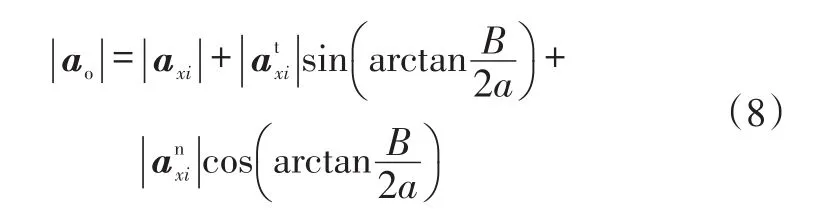
通过仿真对该方法进行验证，仿真工况选择直线加速与转弯加速联合工况，转向盘转角为正弦输入，获得的等效车辆纵向加速度ao如图3所示。

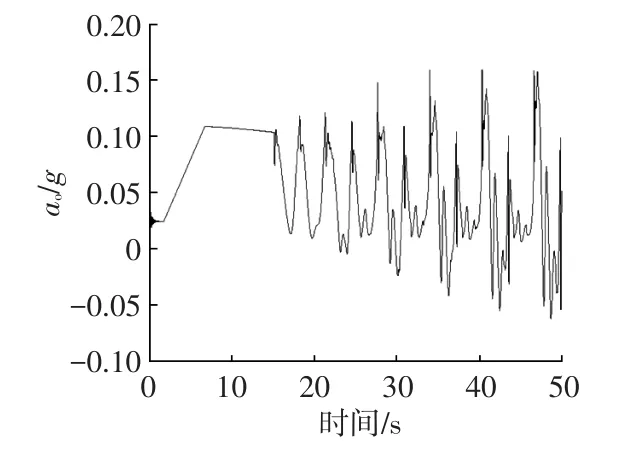
图3 等效车辆纵向加速度

等效车辆纵向加速度反映了车轮没有滑移/滑转情况下的理想车辆纵向加速度。由图3可知，第15 s前车辆做变加速和匀加速运动，第15 s后ao总体呈周期性波动，这与设计工况相符，说明了该方法获得的等效加速度可以在一定程度上反映车辆的运行状态。

2.2 基于模糊规则的单轮稳定性判断

为了更加准确地判断单个车轮的稳定性状态，采用2.1节中获得的等效加速度与传感器采集的实际加速度进行对比判定。等效加速度是假设车轮无滑移/滑转情况下的车辆纵向加速度，而传感器所采集的信号是实车运行过程中车轮存在滑移/滑转时的加速度，因此两者之间的差值可在一定程度上反映车轮滑移/滑转情况，以此作为判断车轮稳定性的依据更为准确。

设车轮线速度为vxi，上一时刻的车速为vxf，2.1节中所求得等效车辆纵向加速度为ao，传感器所采集到的实际车辆纵向加速度为ax，设定滑移/滑转率容差限为Δλ，加速度容差限为ΔA，则单个车轮的失稳判定条件为：

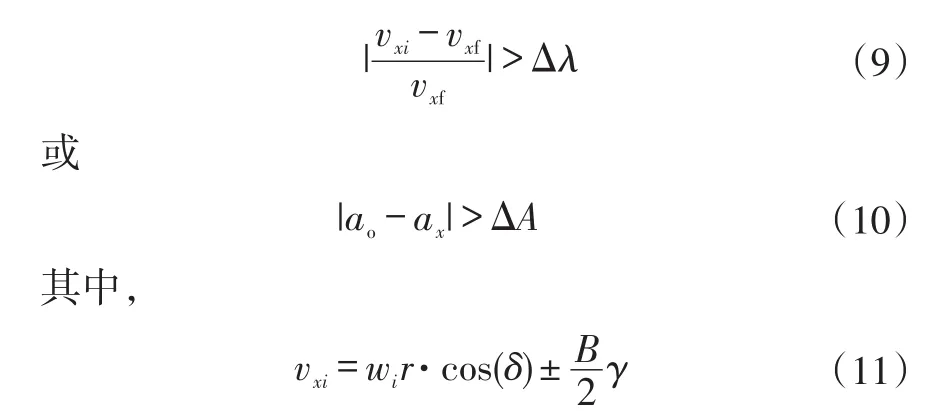
式中，wi为车轮转动角速度。

当满足式（9）、式（10）中任一条件时，判定该车轮不稳定，其轮速不能用于车速估计。对4个车轮分别进行判断，作为车速估计方法选择的依据。

Δλ和ΔA采用自适应模糊控制算法进行实时在线调整，减少整车标定参数数量的同时提高了估计算法的自适应性。例如，在极限情况下适当缩小容差限可以提高通过加速度估计车速的比例，降低对不稳定轮速的依赖，从而提高车速估计精度。考虑到路面附着系数μ以及转向盘转角δw对车轮的滑转/滑移影响较大，将其作为模糊规则的输入。Δλ和ΔA的模糊域及模糊度由仿真试验确定，分别以不同的μ和δw进行分组试验（实车应用时需利用实车试验重新确定该模糊规则）。模糊推理逻辑如表1、表2所示，其中，S、M、L分别表示大、中、小。

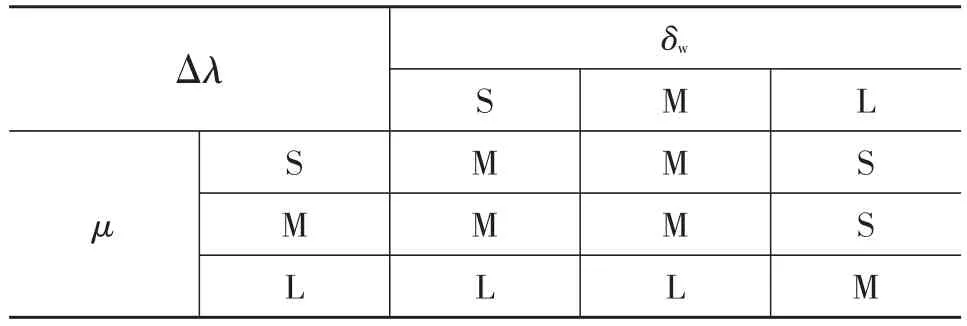
表1 滑移/滑转率容差限模糊规则

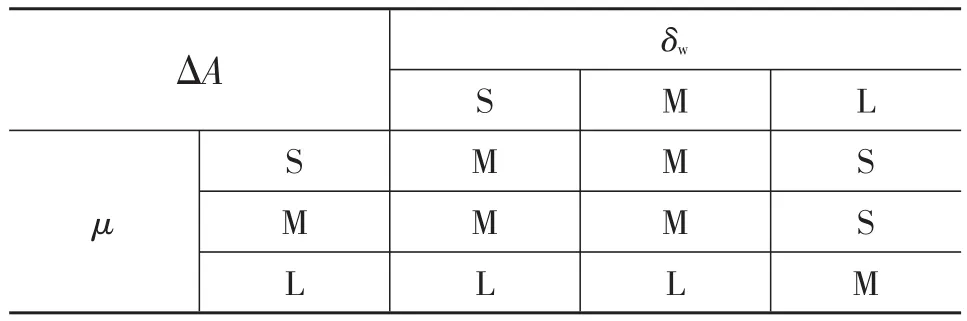
表2 加速度容差限模糊规则

2.3 自适应车速估计方法

车辆在行驶过程中，4个车轮的运行状态实时变化，存在单轮、多轮滑移/滑转或者全轮失稳等情况，本文针对不同情况选择相应的车速估计方法，实时自适应切换车速估计模式。通过Stateflow状态推理机搭建逻辑推理模型，根据车辆4个车轮的稳定性状态自动选择相应的车速估计方法，选择逻辑如图4所示，共有6种模式，主要包括全轮轮速估计、加速度估计、前/后轮轮速估计、单侧轮速估计以及对角轮速估计等。

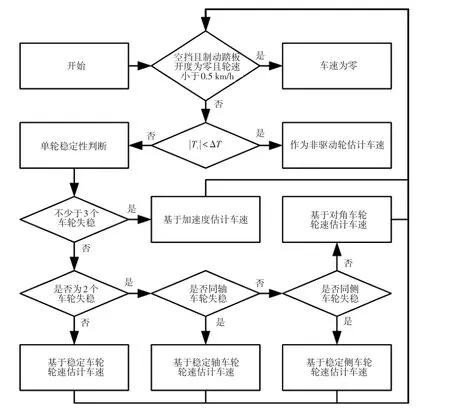
图4 车速估计模式选择逻辑

2.3.1 模式1：非驱动轮/全轮估计模式

a.当4个车轮中有n个转矩小于限定值（即|Ti|＜ΔT）的车轮时，则可将该轮作为非驱动轮，其轮速可以直接作为车速输出，即：

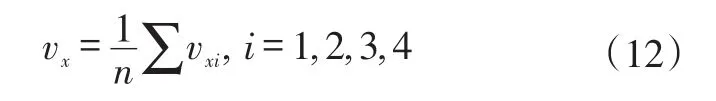
b.当有3个或者3个以上车轮稳定时，若汽车处于驱动状态，则以稳定车轮的最小轮速计算车速：

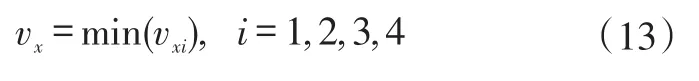
若处于制动状态，则以最大轮速计算车速：

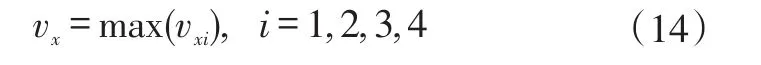
2.3.2 模式2：轮加速度积分模式

当有3个或3个以上车轮发生不稳定情况或者制动踏板开度不为零时，则不能采用轮速估计车速，这时需要通过纵向加速度积分获取车速并用侧向加速度和横摆角速度进行修正。车辆纵向和侧向车速分别为：

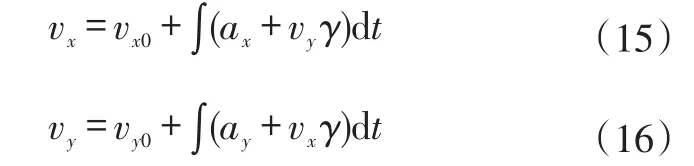
式中，vx0、vy0分别为纵向和侧向初始车速；ay为侧向加速度。

vx0通过比较平均轮速与上一时刻车速来确定，即当两者差值的绝对值大于2 km/h（标定量）时取vx0=，否则vx0=0，这样可以有效判断车辆处于起步过程或运行过程，避免了控制器突然断电重启时积分初始值难以确定的问题；侧向速度初始值为零。

2.3.3 模式3：前轮估计模式

当后轴2个车轮发生不稳定现象时，车速由前轴稳定车轮轮速取均值计算，即：

2.3.4 模式4：后轮估计模式（计算方法同模式3）

2.3.5 模式5：单侧轮估计模式

当同侧2个车轮出现不稳定现象时，车速取稳定侧轮速的平均值并经矫正，即：

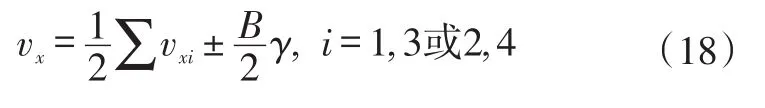
式中，内侧车轮取“+”，外侧车轮取“-”。

2.3.6 模式6：对角轮估计模式

当异侧2个车轮出现不稳定现象时，车速取稳定车轮的轮速平均值，即：

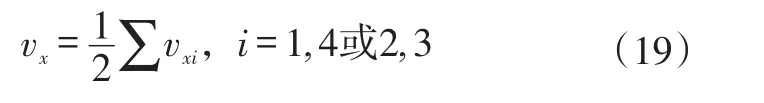
2.4 车速平滑处理

根据工况不同，车辆运行过程中车速估计模式切换会较为频繁，造成估计车速微小突变较多，采用低通滤波器进行处理：

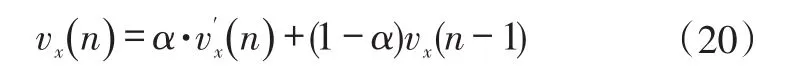
式中，α为滤波系数；为本次采样值；vx(n-1)为上次滤波输出值；vx(n)为本次滤波输出值。

3 仿真验证

采用Simulink/CarSim进行联合仿真，以CarSim的输出车速为目标车速，估计车速与该车速的误差反映了估计精度的高低。

3.1 工况一

为了验证2.1节中基于轮速估计的等效车辆加速度对于车轮稳定性的判定准确性，分别将基于轮速估计的车辆等效纵向加速度ao和直接对轮速微分获得的轮加速度axi代入式（10）判断车轮的稳定性，并进行对应的车速估计，其对比结果如图5所示。图6所示为基于两种车轮稳定性判别方法的车速估计模式选择结果，分别对应2.3节中的模式1～模式6。

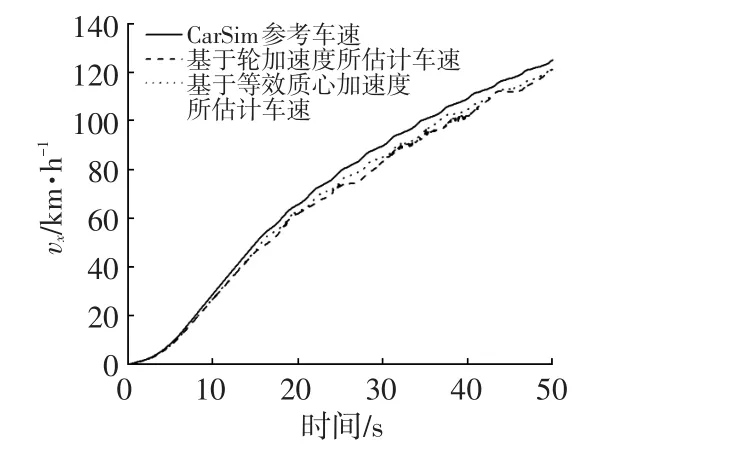
图5 车速估计对比结果

由图5可知，基于等效加速度的车轮稳定性判断结果对车速的估计更加精确。同时，结合图6可以看出，基于轮加速度的车轮稳定性判断模式切换过于频繁，导致估计车速波动更大。

图6 基于两种车轮稳定性判别方法的车速估计模式选择结果

3.2 工况二

为了充分验证本文提出的自适应车速估计方法的有效性，开展不同路面附着系数下的仿真验证，采用四轮驱动、加速转向工况，转向盘转角为正弦输入，路面附着系数分别为0.4、0.5、0.6、0.8进行4次仿真，结果如图7～图10所示。

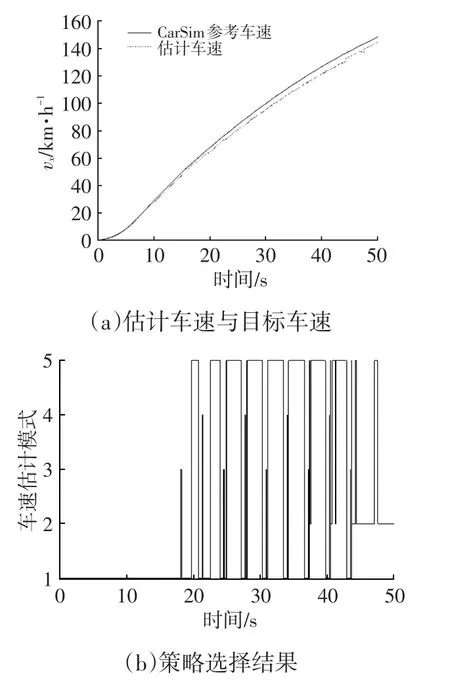
图7 μ=0.4时的仿真结果

由图7a、图8a可知，在路面附着系数较低的情况下该算法也可以对车速进行较精确的估计，说明其适应性强。由图9a、图10a可知，在路面情况较好时，该算法估计的参考车速能够很好地跟踪CarSim中给出的车速，误差不超过5%。由图7b、图8b、图9b、图10b可知，算法可根据单个车轮的稳定性状态自动选择并切换车速估计模式，说明车轮稳定性判断方法有效，模式选择逻辑合理，且随着路面附着系数的下降，车轮处于不稳定的时间增加，采用加速度估计车速的比例逐渐提高。

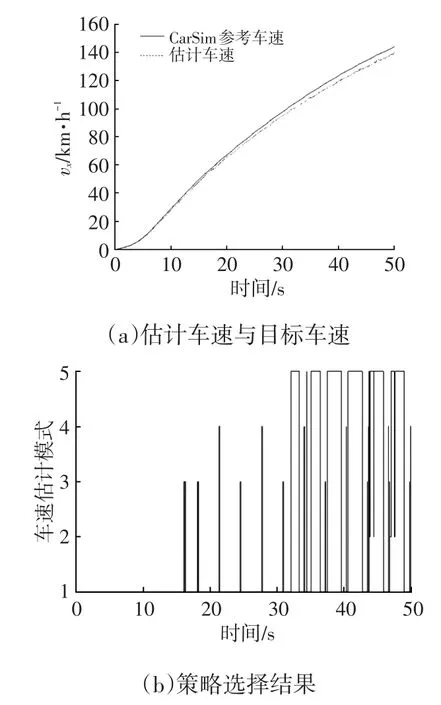
图8 μ=0.5时的仿真结果

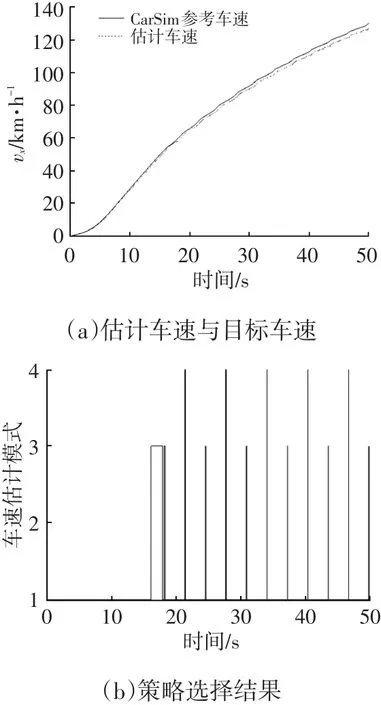
图9 μ=0.6时的仿真结果

4 硬件在环试验验证

本文使用的硬件在环试验平台由dSPACE1005、dSPACE1104以及搭载Infineon-TriCore芯片的整车控制器组成，本文提出的车速估计算法在整车控制器中运行，基于CarSim的整车实时模型在dSPACE环境中运行。

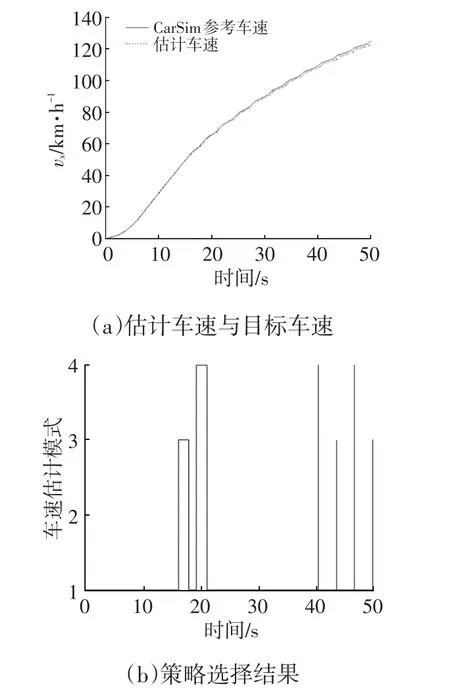
图10 μ=0.8时的仿真结果

设转向盘转角为正弦激励（幅值为180°）、路面附着系数为0.5，工况由加速、等速、转向及制动过程组成。试验结果如图11所示。

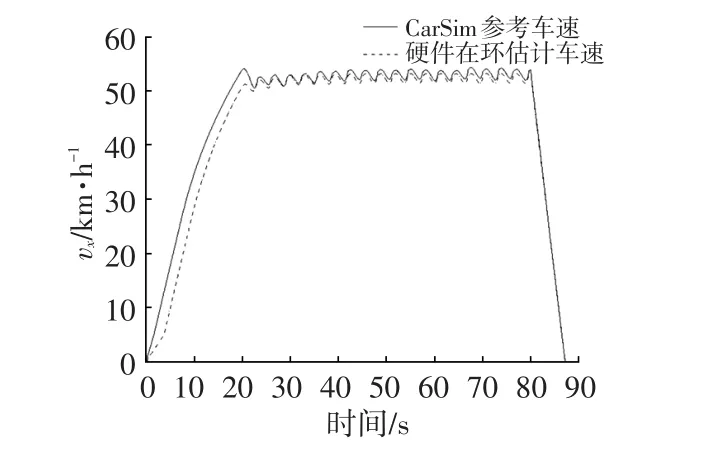
图11 车速硬件在环试验结果

由图11可以看出，硬件在环环境下通过控制器计算出的估计车速与目标车速基本一致，说明该方法可以较准确地对车速进行估计，具有实车应用价值。

5 结束语

本文对四轮独立驱动电动汽车的纵向车速估计进行了研究，提出了一种多模式自适应车速在线估计方法，并通过仿真和硬件在环试验进行了验证，结果表明：相对于直接通过轮加速度判断车轮的稳定性，等效车辆纵向加速度的引入能够更加准确地判断每个车轮的稳定性状态，从而更加合理地选择车速估计方法，提高估计精度；本文提出的车速在线估计方法估计精度较高，具备实车应用的条件。

本文提出的轮加速度与车辆纵向加速度关系式的严谨性与准确性还有待提高，文中引用的多个参数较难获取，例如车轮有效滚动半径和路面附着系数，这些参数本文只进行粗略估算，其估算误差的引入也将会对车速估计精度产生影响，是后续研究的重要内容。