基于稳态转向特性的智能车辆换道轨迹规划＊

张新锋 李传友 夏八科

（1.长安大学，汽车运输安全保障技术交通行业重点实验室，西安 710064；2.长安大学，汽车学院，西安710064）

主题词：智能车辆 换道 轨迹规划 转向特性 安全距离模型

1 前言

我国高速公路里程仅占公路总里程的2.5%，但其死亡人数却占公路交通死亡总人数的14%，高速公路上由驾驶员造成的事故占总数的74%[1-2]。汽车智能化发展在减少交通事故、缓解交通压力等方面存在巨大潜能，已成为世界各国的研究热点。其中，轨迹规划是智能车辆研究的重点内容之一，是指生成一段在未来时间和空间内的行驶轨迹[3]。而换道是车辆最基本的驾驶行为，智能车辆换道轨迹规划的研究对提高公路交通安全性、提高交通效率具有重要意义。

目前，国内外学者从不同角度对智能车辆的轨迹规划问题展开了研究。陈成等人提出一种基于四阶贝塞尔曲线的轨迹规划方法，并通过参数优化规划出曲率变化最小的轨迹曲线，但对交通车的考虑较少，实际应用较为困难[4]。杨志刚等人提出了等速偏移轨迹函数和正弦函数叠加换道模型，解决了一部分换道模型的不足，但没有考虑车辆的实际行驶环境[5]。Chien-Sheng提出了基于多项式函数的轨迹规划方法，建立了加速度约束，速度边界和路径时间最优的多项式参数化仿真模型，为更为精细和完整的动力学模型提供参考[6]。郭枭鹏通过结合人工势场算法和快速搜索随机树算法，实现了实时轨迹规划，但没有考虑轨迹的最优化选取和动力学约束，存在一定缺陷[7]。

利用多项式生成换道轨迹具有参数易获取、曲线多阶连续且易于扩展的优点。本文利用多项式函数进行换道轨迹规划，引入轨迹优化函数和车辆动力学约束，防止车辆出现危险工况，并建立了换道安全距离模型，保证换道安全性。

2 基于多项式的换道轨迹规划

本文研究智能车辆在高速公路上的换道轨迹规划，主要考虑所在车道前车速度过低时，为摆脱低速行驶而进行的换道行为。高速公路具有单侧所有车辆同向行驶、道路坡度平缓、存在连续曲率且曲率较小、可保障汽车高速行驶的特点。由于换道情景较为复杂，为了简化模型，作如下假设：

a.由于换道持续时间较短，一般为4 s左右，忽略换道过程中的速度变化；

b.所有车辆规格相同，即车辆长度、宽度相同；

c.换道过程中，换道车辆纵向运动与横向运动相对独立。

2.1 无交通车轨迹规划

如图1所示，以初始状态车辆质心为原点，以行驶方向为x轴正方向，y轴垂直于x轴指向行驶方向左侧。换道车辆初始状态可以通过车载传感器获得，目标位置状态根据行驶目标设计。本文选择含有6个参数的五次多项式分别描述纵向和侧向轨迹，车辆换道轨迹函数可表示为：

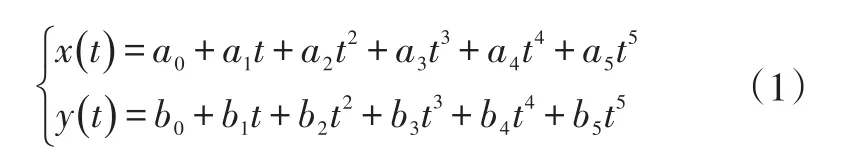
式中，x(t)、y(t)分别为车辆换道过程中的横、纵坐标；t为时间；a0～a5、b0～b5分别为多项式系数。

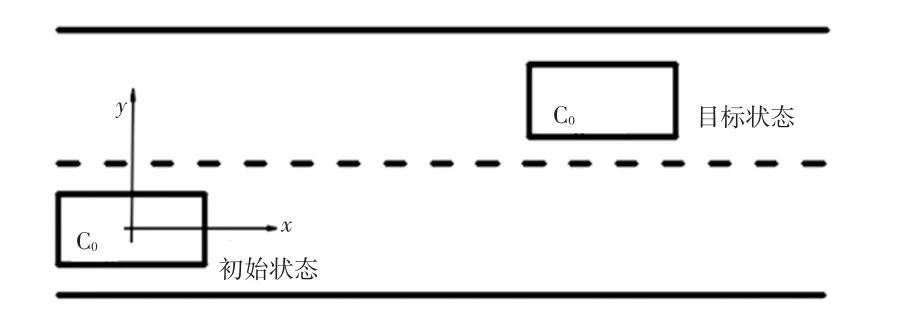
图1 换道状态

车辆在初始位置的坐标为(x0,y0)，x方向初始速度和加速度分别为vx0、ax0，y方向初始速度和加速度分别为vy0、ay0；车辆在目标位置的坐标为(xf,yf)，x方向速度和加速度分别为vxf、axf，y方向速度和加速度分别为vyf、ayf。由于车辆进行匀速换道，vx0=vxf=vc0（vc0为车辆质心速度），ax0=axf=0，车辆在初始位置和目标位置平行于车道线运动，ay0=ayf=0。设车辆换道的初始时刻为t0，到达目标位置的时刻为tf，则根据初始状态和目标位置状态可得：

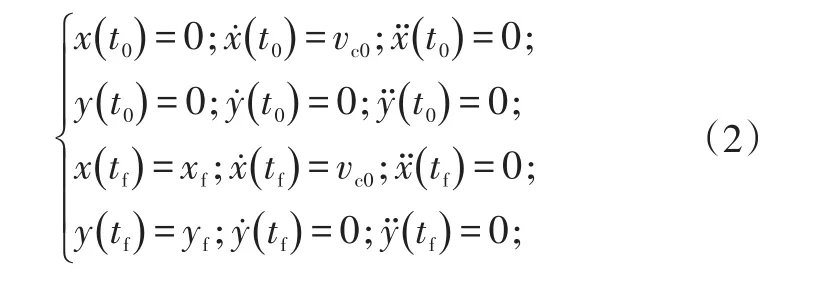
式中，yf与车道宽度相等，取yf=3.5 m；xf=vc0·tf。

式（2）中仅tf为未知量，因此可用tf表示多项式的各系数，tf确定后即可确定换道轨迹。联立式（1）、式（2）可得换道轨迹函数为：

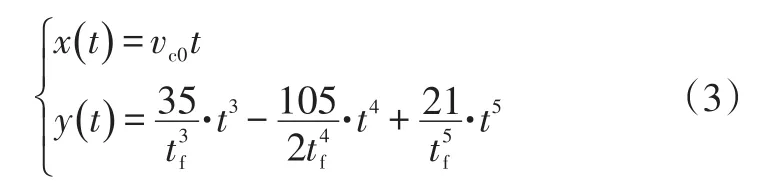
2.2 典型换道工况轨迹规划

在实际的典型换道工况中，交通车对换道车辆的影响不可忽视，其运动状态的估计是进行轨迹规划的前提。交通车的运动学方程可表示为[8]：

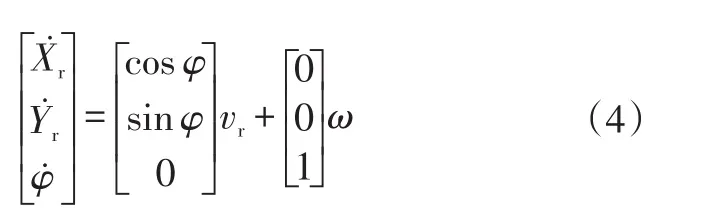
交通车的初始状态可由车载传感器获得，但其运动学方程的输入vr和ω未知，故其未来状态未知。在实际行驶中，交通车大多遵循基本交通规则，因此本文合理假设，在较短的运动周期内，交通车保持当前运动状态不变，即交通车沿车道中心线匀速行驶：

式中，xt、yt分别为t时刻交通车在x、y方向的坐标；vx为交通车在x方向上的速度；(xi,yi)为ti时刻交通车的位置坐标。

换道过程中的潜在危险工况是主车未能充分进入相邻车道时与交通车发生碰撞。本文假设主车在换道过程中以平动的方式运动，由于航向角较小，且其横向位移远大于纵向位移，可假设换道过程中汽车与车道中心线的夹角近似为零。

如图2所示，主车在换道初始时刻以vc0速度行驶，探测到前方距离为S处存在交通车，该车以vcf匀速行驶。假设目标车道有安全换道空间，若vc0≤vcf，两车不会相遇，按无障碍车进行轨迹规划，若vc0＞vcf，假设主车经过tc时间后与交通车的距离为换道间距宽裕度[9]Sw，此时，若主车侧向行驶距离大于交通车的宽度W，则主车已安全避开交通车，换道过程无碰撞风险，其间主车和交通车行驶的距离分别为Sc0tc和Scftc。

联立式（3）、式（6）、式（7）可得：

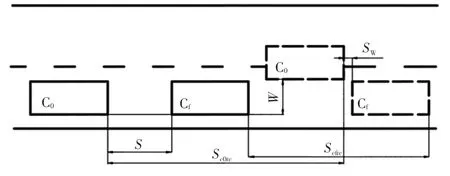
图2 典型工况换道示意

由此可以通过限制tc时刻主车的侧向位移，安全避开前方的交通车，实现安全换道。

3 约束条件与换道安全距离模型

3.1 约束条件

3.1.1 轨迹曲率约束

车辆在高速路上行驶时，需要考虑换道车辆的动力学约束和执行机构的约束，规划结果需保证换道路径的曲率连续且处于合适的范围。本文利用稳态车辆二自由度微分方程对换道车辆的侧向加速度、前轮转角和车速进行分析，得出换道路径曲率与车速和侧向加速度的关系，进而对换道路径的曲率进行限制，满足换道车辆动力学约束。

汽车运动微分方程为：

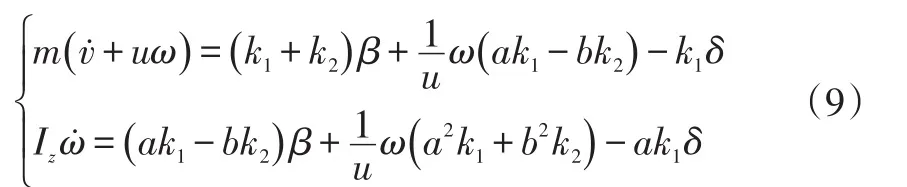
式中，δ为前轮转角；k1、k2分别为车辆前、后轮侧偏刚度；β=v/u为质心侧偏角；Iz为汽车绕Z轴的转动惯量；u为质心速度在x轴的分量；v为质心速度在y方向上的分量；a、b分别为质心到前、后轴的距离；m为汽车总质量。

根据稳态时汽车二自由度微分方程可得侧向加速度与前轮转角和速度的关系为：

式中，K为稳定性因数；g为重力加速度；L为车辆轴距。

由于车辆质心侧偏角较小，可以认为质心速度与u相等，速度一定时，前轮转角满足：

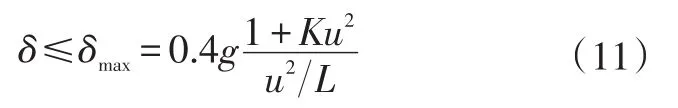
稳态横摆角速度增益为：

又因v=ω·r，联立式（11）、式（12）可得转向半径为：

则换道路径曲率为：

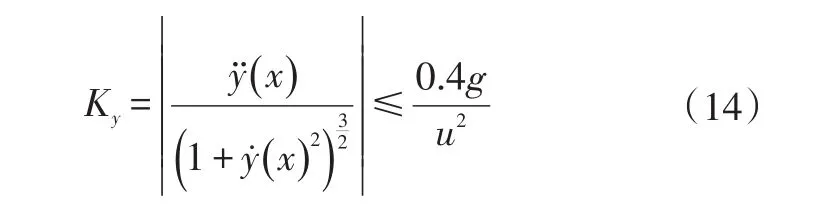
本文考虑车辆在高速公路的换道工况，故车速范围设为60～120 km/h，不考虑车辆低速时的最小转弯半径。根据轨迹函数y(t)可知曲率的最大值存在于tf/4处，则换道路径最大曲率为：

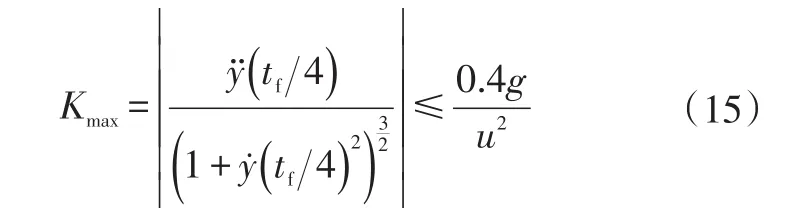
可得tf≥fk(u)，fk(u)为依据式（15）求得的tf关于u的函数。确定tf的最小值即可确定换道车辆在速度为u时的换道路径最大曲率，保证换道平稳性。图3所示为车速在25 m/s时依据不同tf规划所得的轨迹族曲线，其中极限换道轨迹是依据稳态转向特性所求得的最大曲率轨迹曲线，其左侧为易发生侧滑的危险换道轨迹，右侧为安全换道轨迹。

图3 轨迹族曲线

3.1.2 轨迹优化函数及其求解

在换道轨迹规划中，tf的值一般根据经验获得，具有很大的不确定性，本文通过引入换道轨迹优化函数J对其进行最优化选取。J的确定需要兼顾车辆的行驶效率、安全性、经济型和舒适性。为了简化运算复杂度，提高轨迹规划的实时性，本文以车辆的行驶效率、安全性和舒适性为优化目标，在换道过程中，车辆安全隐患主要为换道车辆越过道路边界，与交通车发生碰撞，在规划算法中已对车辆的侧向位移提出约束，对换道安全距离进行单独分析，安全性得到保障。车辆的最大侧向加速度越大，舒适性越差，而换道耗费时间越久，行驶效率越低。本文以车辆最大侧向加速度aymax和换道时间为优化变量，为弥补两个指标在数量级上的差异，对两者均进行无量纲化处理。引入函数：

式中，ay＜aymax；tfmin＜tf＜tfmax；tfmin=fk(v)为最小换道时间；tfmax为最大换道时间。

则轨迹优化函数为：

对于轨迹优化函数将ay和tf作为优化变量的情况，引入遗传算法对其进行求解。在遗传算法中，设种群个体数目为40，最大遗传代数为20，代沟为0.95，交叉概率为0.7，变异概率为0.01。本文选用二进制编码，染色体X的形式可表示为：

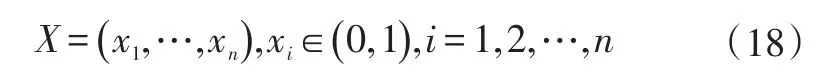
式中，n为种群规模。

本文将轨迹规划中的轨迹优化函数作为遗传算法的目标函数和适应度，定义为：

将轮盘赌选择算子作为遗传算法的选择算子，个体的适应值越高，被选择的几率越大，被选择概率可表示为：

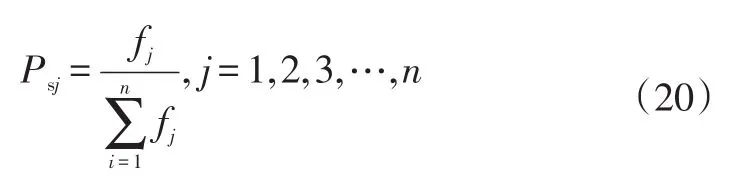
式中，fj为个体j的适应值。

在约束条件的设置中，采用搜索空间限定法，加入对轨迹优化函数参数的约束和车辆自身的约束：

3.2 换道安全距离模型

图4所示为一种典型的换道工况，主车C0在当前车道行驶，车道前方和后方有交通车Cf和Cr，目标车道存在交通车 Clf和 Clr。Cf、Cr、Clf和 Clr是影响换道安全性的主要因素，在换道安全性分析中，Cr与C0的安全性主要由 Cr负责，故不再讨论。本文主要对 Clf、Clr和 Cf对 C0换道安全性的影响进行分析。

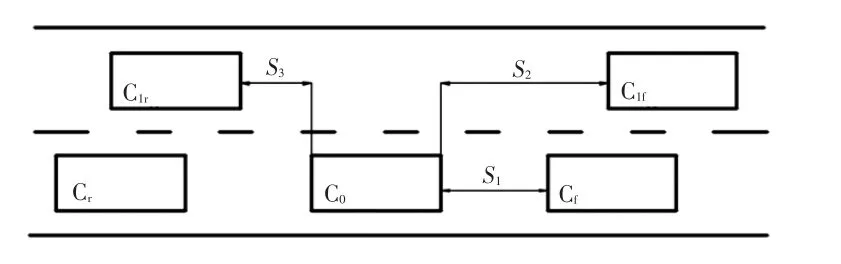
图4 典型换道工况

3.2.1 目标车道换道安全性分析

目标车道交通车对换道安全性的影响主要为C0进入目标车道时因换道空间不足与Clf或Clr发生碰撞。C0与Clf、Clr的距离可由传感器测得，Clf、Clr在目标车道保持匀速行驶，假设C0在当前时刻进行换道，预测换道结束后C0与Clf、Clr的距离，通过判断其是否满足换道安全距离要求确定当前时刻是否可以安全换道。换道完成时，C0与Clf的距离可表示为：

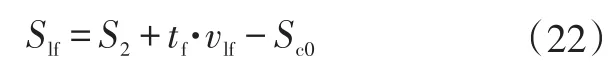
式中，vlf为 Clf的车速；S2为换道前C0与 Clf的距离；Sc0为C0在换道期间的纵向行驶距离。

车辆跟随模式的主动避撞安全距离模型[10]为：

式中，Dsf为主动避撞安全距离；vrel=vlf-vc0为C0与Clf的相对速度；δa=0.52vc0-0.121 5为期望相对减速度；df1=0.850 9vf+1.610 9为相对减速度消除后C0与Clf的距离。

在换道结束后，主车与前车需要保持的安全距离遵循主动避障安全距离，即当Slf≥Dsf时可执行换道。

完成换道时C0与Clr的距离可表示为：

式中，S3为换道前C0与Clf的距离；vlr为Clr的车速。

当vc0≥vlr时，若S3≥0，C0与Clr不会发生碰撞；当vc0＜vlr时，C0与Clr之间应保持主动安全距离：

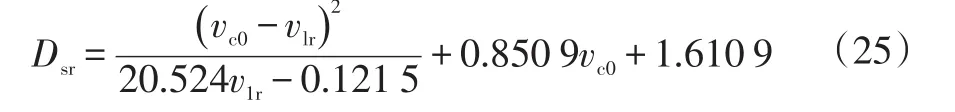
换道结束后，C0与Clr需要保持的安全距离遵循主动碰撞安全距离模式，即当Slr≥Dsr时可执行换道。

3.2.2 当前车道安全性分析

由式（17）可知，当Kmax=0.4g/v2、换道轨迹为极限换道轨迹时换道轨迹曲率最大、换道时间最短，即tfmin=fmin(v)，则最小安全换道纵向距离为x(tfmin)=vc0tfmin。在最小安全换道距离下，要安全避开Cf需满足y(tcmin)＞W，则安全换道情况下C0与Cf最小安全距离为DS-cfmin=vc0tcminvcftcmin。换道前C0与Cf需满足纵向最小安全距离：

式中，S1为换道前C0与Cf的距离。

通过以上分析可以得到满足车辆安全性的换道安全距离模型为：

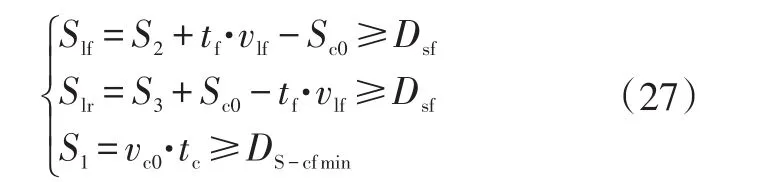
当C0与Cf以及Clf与Clr满足以上条件时可执行换道。

4 仿真分析

设主车在换道时的初始速度为25 m/s，在t0时刻开始换道，结束换道时主车的横向加速度、侧向加速度均为0，车道宽度取为3.5 m，在MATLAB和CarSim中分别进行无交通车和典型换道工况下的规划仿真和动力学仿真，采用的参考车型轴距为2 910 mm，路面为附着系数为0.85的混凝土路面。

4.1 无交通车轨迹规划仿真

设同车道和相邻车道无交通车，C0车速恒定为25 m/s，无制动，转向模式为驾驶员轨迹跟随模式。仿真结果如图5所示：由图5a可求得最优换道时间为4.85 s；由图5b可以看出，当前规划轨迹在极限换道轨迹右侧，满足转向特性约束；由图5c～图5e可知，侧向加速度、横摆角速度和轨迹偏离值在合理范围内。

4.2 典型换道工况轨迹规划仿真

设Cf以18 m/s匀速在车道中心线上行驶，S1=15 m，Clf、Clr分别以30 m/s和28 m/s的速度匀速行驶，S2=35 m，S3=40 m。对各车距进行安全距离判定，由优化函数和最大曲率限制可得，当前工况最优换道时间为3.88 s，当前车速下最短换道时间为2.1 s。由式（27）可知，各车距符合换道安全距离模型，可执行换道。

仿真结果如图6所示，由图6a可得最优换道时间为3.88 s，由图6b可以看出，当前规划轨迹在极限换道轨迹右侧，满足转向特性约束，由图6c～图6e可知，侧向加速度、横摆角速度和轨迹偏离值均在合理范围内。

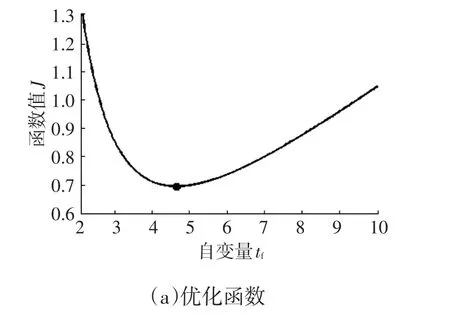
图5 无障碍换道仿真结果

通过仿真可以看出，在无障碍和典型换道工况下换道时，规划出的轨迹曲线满足车辆换道需求，侧向加速度和横摆角速度在合理的范围内，车辆的舒适性和稳定性较高，轨迹偏离值在一定范围内，轨迹的可跟踪性能可得到满足。

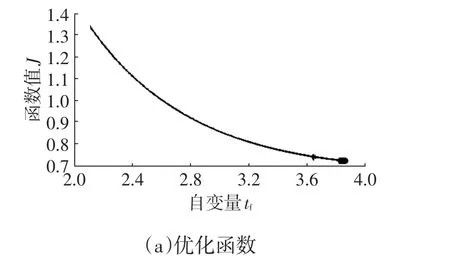
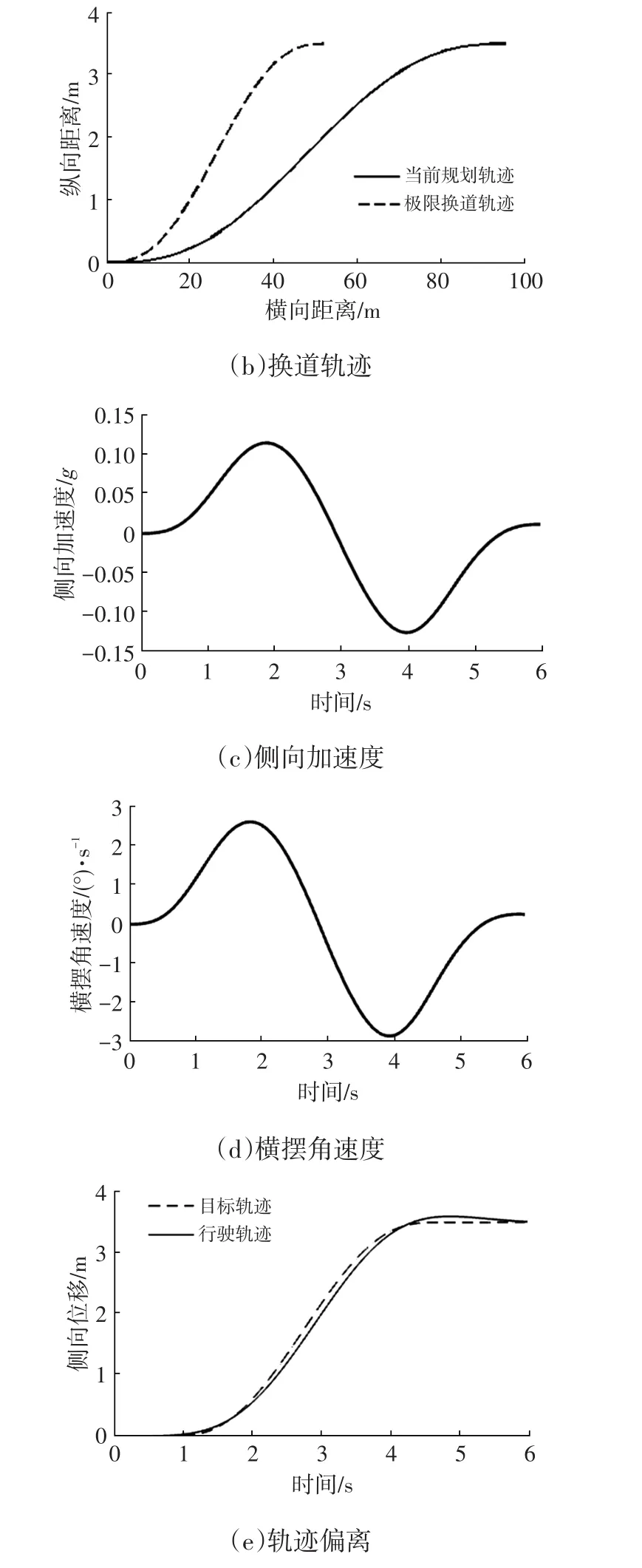
图6 动态换道轨迹仿真结果

5 结束语

本文提出了一种考虑高速时稳态转向特性的换道轨迹规划方法，利用多项式函数建立换道轨迹模型，引入以换道时间和侧向加速度为变量的轨迹优化函数对轨迹进行最优选取，降低了依靠经验选取换道时间的不确定性。同时，建立了换道安全距离模型，保证车辆换道的安全性，基于车辆稳态转向特性对轨迹曲线的曲率进行限制，通过确定车辆在稳态转向特性下允许的最大换道轨迹曲率对车辆的最小换道时间进行限制，避免车辆在高速时因轨迹曲率过大发生侧滑现象。最后，通过仿真分析验证了该方法的合理性。