基于时域差动成像的车辆精细运动轨迹重构方法

张辉 陈静萍 林军记 王浩远 龚文森

（中山大学 智能交通研究中心，广东省智能交通系统重点实验室，广州 510006）

主题词：差动成像 汽车轨迹 速度积分 汽车运动参数 图像匹配

1 前言

在智能车运动控制、智能网联汽车协同运行、事故现场复现、车辆微观驾驶状态观测等领域，准确感知车辆运动轨迹的细节都具有重要的作用。目前，一般采用卫星定位技术、蜂窝无线定位技术，通过解算序列化的定位信息复现车辆的运动轨迹，但往往由于序列定位点的精度较差，无法准确感知车辆变道、泊车等运动过程的精细轨迹。为了解决这一问题，在无人车领域常采用高精度差分卫星定位系统，通过厘米级精度的序列定位点来重构车辆的精细运动轨迹，但采用这类系统成本一般较高，且往往受到环境条件的影响[1-4]。另一类获取车辆精细运动轨迹的方法是惯性导航技术，这类技术主要使用惯性传感器检测汽车在惯性参考系中的惯性加速度和欧拉角速度等惯性参数，利用牛顿运动定律和动坐标系角速度转换进行逐点推算，通过积分计算得出汽车运动位置。但是，其轨迹感知性能在很大程度上依赖于惯性传感器的性能以及车辆本身的固有特性，载荷的动态变化、道路条件的差异等各种因素都可能导致轨迹感知的巨大误差积累[5-8]。

有学者提出采用汽车图像匹配技术对环境进行初步检测，主要是基于两帧计算框架，选取两帧图像中的特征点，基于所获得的特征关联集合进行帧间位姿估计，可以实现车辆的定位和运动估计。然后结合导航卫星、传感器或者蜂窝无线技术检测汽车自身的运动参数，进而实现汽车运动轨迹的感知。由于此类方法多采用前视图像，感知的车辆轨迹仍然不够精细[9-10]。

为此，本文提出了一种高精度、低成本，不依赖辅助设施的车辆精细运动轨迹感知方法。通过时域差动成像的方法，首先使用光轴垂直于地面的摄像头获取车辆所在路面的细节图像，利用对路面图像细节在差动时间内偏移量的识别与匹配，计算车辆相对于路面的运动速度、方向、横摆角，进而根据速度积分法实现汽车精细轨迹重构与感知。

2 车辆运动轨迹差动成像重构原理

车辆的运动轨迹可以通过车辆精确位置坐标时间序列获取，也可以通过车辆运动参数依据动力学原理进行推算，本文研究的方法在不依赖车辆的精确位置坐标的条件下实现车辆运动轨迹的感知，因此采用常用的动力学推算方法——速度积分法重构车辆的精细运动轨迹，同时讨论获取速度积分所需参数的方法。

2.1 速度积分法

速度积分法[11]重构车辆运动轨迹的原理如图1所示。首先，定义车辆二维坐标系，原点为车辆中心，车辆运动方向为横轴正方向，横轴逆时针旋转90°为纵轴方向。图中坐标系XOY为大地坐标系，且与车辆初始状态的车辆坐标系重合；坐标系Xk-1Ok-1Yk-1、XkOkYk分别为(k-1)和k时刻的地面坐标系，且分别与相应时刻的车辆坐标系重合；vk和uk分别为k时刻车辆在坐标系XkOkYk中的纵向速度和横向速度；ψk为k时刻车辆坐标系横轴与坐标系XOY横轴的夹角，即横摆角；φk为车辆坐标系横轴与大地坐标系XOY横轴的夹角在(k-1)至k时刻期间的增量，在此定义为“瞬态横摆角”。

图1 速度积分法原理示意

根据速度积分原理，在离散情况下车辆位置的轨迹序列为(xn,yn),n=0,1,2,…，可以表示为：

式中，T为两次采样的间隔，即(k-1)和k时刻的时间差。

T足够小时，所计算的轨迹序列无限逼近真实轨迹，且车辆坐标系横轴与大地坐标系XOY横轴夹角的累计值为：

其中，定义φ0=0、x0=0、y0=0，则只要感知和检测到车辆在采样时刻k的纵向速度vk、横向速度uk和瞬态横摆角φk，即可重构出车辆的运动轨迹。

2.2 差动成像车辆运动参数检测原理

传统的速度积分法利用陀螺仪测量出汽车的角速度在汽车坐标系上的分量，利用五轮仪或加速度计测量出汽车的速度和加速度在汽车坐标系上的分量，经过积分与变换重构出汽车的质心轨迹。本文通过车载设备的差动成像提取车辆的纵向速度、横向速度和瞬态横摆角。

在此，差动成像是指间隔一定时间，具有一定视场重合度的两次成像工作模式，利用差动成像提取车辆运动参数的原理如图2所示。在车辆运动过程中，通过车载设备差动成像对路面进行拍摄，则第k次差动成像会在Δ时间间隔连续获取2帧图像，即A帧图像和B帧图像，如图2a所示；此时，路面特征点（如图2中Ⅰ、Ⅱ、Ⅲ）将分别呈现在2帧图像上，但其坐标有所区别，如图2b、图2c所示。特征点的坐标差别可以反映出车辆相对于路面的位移和横摆运动，从而获取车速和横摆角速度。

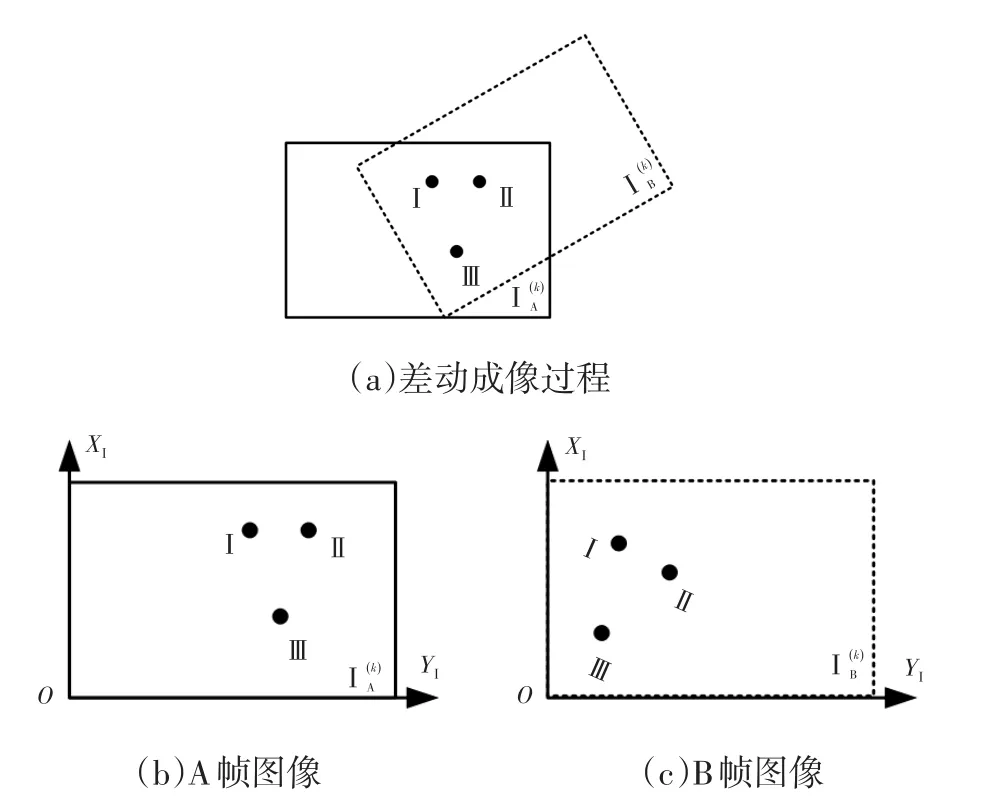
图2 差动成像运动参数检测原理

式中，D为两坐标系之间的平移距离向量[dxdy]T；dx、dy分别为横向和纵向位移量；PA和PB分别为特征点在和中的坐标矩阵为旋转矩阵；β为两帧图像的相对旋转角。

利用图像识别技术获取各特征点在两帧图像中的坐标，求解式（3）中的D和β，经过图像距离与地面距离的尺度增益，可得k时刻的车辆运动参数：

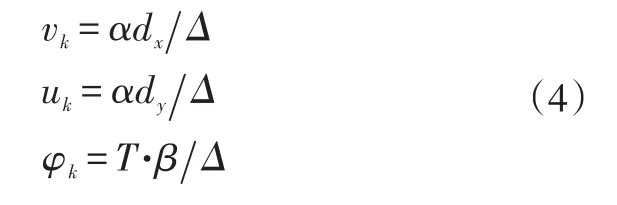
式中，α=H/f为尺度增益；H为差动成像设备与路面间的高度差；f为成像系统特性参数（可通过标定试验获得）；Δ为间隔时间。

3 差动成像轨迹重构的实现

3.1 时域差动成像设计

时域差动成像的核心是间隔时间Δ完成连续2帧图像的采集，最简单的实现方法是采用单个摄像头的连续2帧图像，此时T=Δ。但车速较快时，由于单个摄像头的帧率较低（25帧/s）或视场较小，导致相邻2帧图像间无重叠部分，无法通过该方法进行检测，而高帧率摄像头的成本较高，且无法适应高速情况或者速度变化较大的情况[12]。为了解决这一问题，本文设计了采用双摄像头的差动成像方案，其基本原理如图3所示。

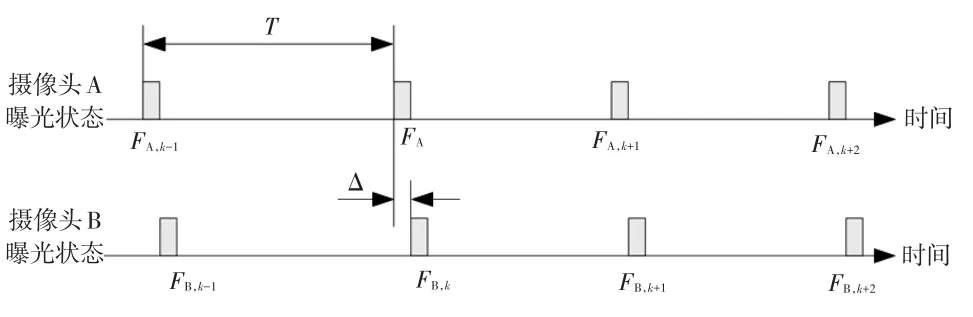
图3 双摄像头时域差动成像原理

由图3可以看出，摄像头A和摄像头B帧率虽均很低，一般T=40 ms，但可以通过控制2个摄像头的启动时刻，使曝光帧FA,k和FB,k的时间间隔为Δ。

为此，设计时域差动控制和光路结构分别如图4、图5所示。图4中，将2个摄像头的独立时钟改为共用时钟，以保证两者的时钟同步，同时采用单片机控制其启动时刻，实现两者的差动成像，差动时间1～40 ms可调。图5所示的双摄像头光路结构，使用立方体分光棱镜确保2个摄像头的视场保持一致，避免检测区域减小。

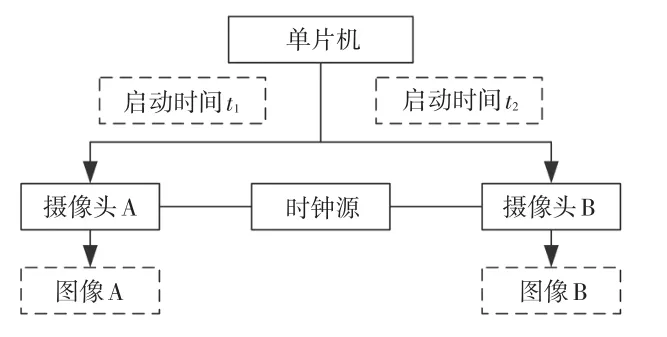
图4 差动控制示意

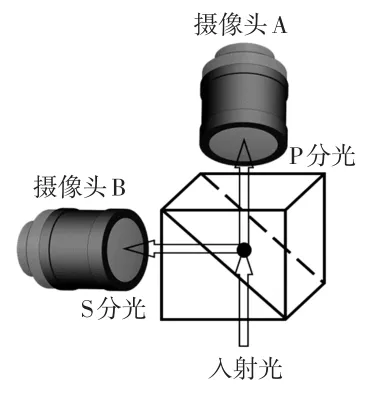
图5 立方体分光棱镜

3.2 图像匹配方法

本文选用加速鲁棒性特征（Speeded Up Robust Features，SURF）匹配算法[13-14]进行图像匹配。Hessian矩阵是SURF匹配算法的核心，图像中的某一点是否为图像的极值点可以使用Hessian矩阵及其判别式来判定，从而检测出图像中的特征点及其位置与尺度[16]。假设图像中的某一点为I(U,V)，图像尺度为σ，则该点的Hessian矩阵为：

则该点的Hessian矩阵的判别式为：

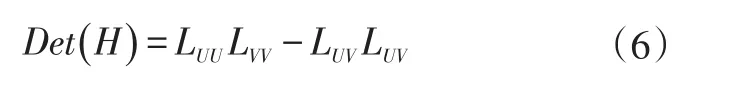
当Hessian矩阵的判别式取得局部极大值或极小值时，判定当前点较周围邻域内其他点更亮或更暗，由此定位关键点，可以检测出图像在尺度σ下特征点的响应值，遍历所有像素，即可检测出该尺度下所有的特征点。SURF匹配算法采用不断增大滤波器模板尺寸求取Hessian矩阵响应值，求取不同尺度下的特征点。

在检测出特征点后，对其进行特征向量描述。首先求得特征点的主方向，以y表示沿主方向，x表示垂直于主方向。为了描述特征点，首先以该点为中心，取20s×20s（s为该点所在图像的尺度值）的图像，将该图像划分为4×4共16个子块，每个子块内有5s×5s个像素。对每个子块进行Haar小波响应值计算，分别得到dy、dx及对应的绝对值|dy|和|dx|。

对需要匹配的图像进行特征向量匹配，以特征向量间的欧几里得度量作为相似性度量的结果，采用基于欧几里得度量的最邻比较法来实现。将图像A中任意一个特征点与图像B中欧几里得度量最小的2个特征点进行比较，当度量最小的点小于度量次小的点一定比例时匹配成功。匹配得到的结果如图6所示。

3.3 系统误差校正

有2类系统误差对轨迹的重构产生较大影响，分别是成像光路带来的图像畸变和车辆承载状态带来的成像高度差变化。系统应用中必须对其进行校正。

图6 SURF匹配结果

3.3.1 图像畸变校正

图像畸变校正的方法已经非常成熟，本文采用网格模板法[15]进行畸变校正。通过对标准网格模板进行拍摄，获取理想像素坐标与相应畸变像素坐标的对应关系：

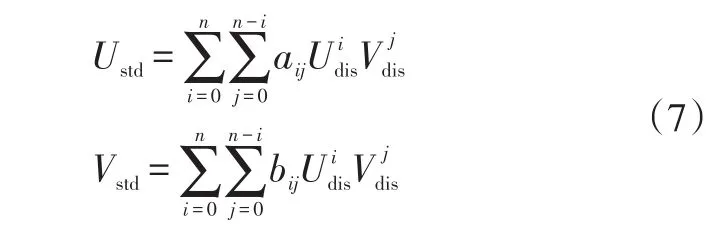
式中，aij、bij为待定系数；n为多项式的次数。

利用曲面拟合方法拟合选取的控制点对，然后用最小二乘法求出待定系数aij与bij，就可以得到理想像素坐标与畸变像素坐标之间的映射关系，完成图像畸变校正。

3.3.2 侧倾与高度误差校正

由于汽车自身的振动、轮胎的压力变化、路面的起伏变化等原因，运动过程中安装在汽车上的差动图像试验平台与地面的相对位置会发生变化，一般情况下其影响不大，但是车辆重载时误差不可忽略。针对该问题，本文在试验平台中加入激光发射器模块，利用激光光斑与路面的图像分析出激光发射器、差动摄像头、路面三者的相对位置关系，从而实现汽车侧倾角和汽车垂直高度的实时检测，其具体实现方法见文献[16]。

4 试验与结果分析

为了检验基于差动图像的汽车精细轨迹重构方法在实车条件下的性能，本文设计了实车连续轨迹重构试验。将差动图像试验平台固定在汽车外部可以观测到路面的位置，记录汽车的起始位置和终点位置作为轨迹重构的参考位置。试验过程中，差动图像试验平台拍摄得到连续的路面图像，同时使用GPS与惯性传感器进行测量，利用测得的数据进行轨迹重构，得到的试验结果如图7所示。

从图7可以看出，汽车进行前进、转弯、倒车等运动时，差动图像试验平台能够比较精确地匹配运动轨迹起点与终点的实际位置，误差较小。本方法试验平台重构的轨迹与GPS和惯性传感器重构的轨迹走势一致，虽然无法获取真实的运动轨迹，但本文提出的方法终点位置误差小于GPS与惯性传感器轨迹重构的终点位置误差，如表1所示。这一结果表明，基于差动图像的汽车精细轨迹重构方法具有较高的精度。其中，3种方法的理论值存在差异的原因是试验时3种测量装置在车辆上的安装位置存在前后差异。GPS的数据误差是由于试验现场的差分基站信号不稳定造成的，因此其误差远大于系统的标称误差。

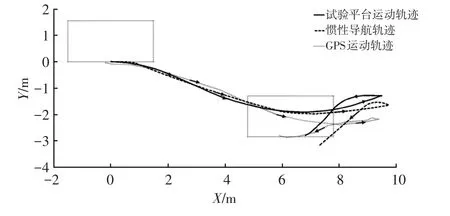
图7 汽车连续轨迹重构结果

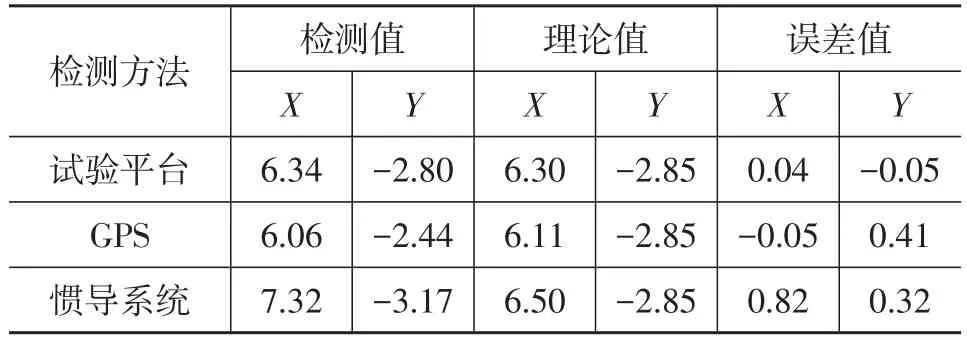
表1 轨迹终点检测结果 m

使用基于差动图像的汽车精细轨迹重构方法一方面能够重构汽车的运动轨迹，另一方面根据速度积分法的特性，在计算过程中能够得到各时刻相对于大地坐标系的横摆角，因此本方法能够将汽车运动过程中车身姿态的精细变化进行重现。试验结果如图8所示，这一结果可以有效反映车辆运动中所占用的空间，对于车辆的运动控制和轨迹规划起到重要的反馈作用。

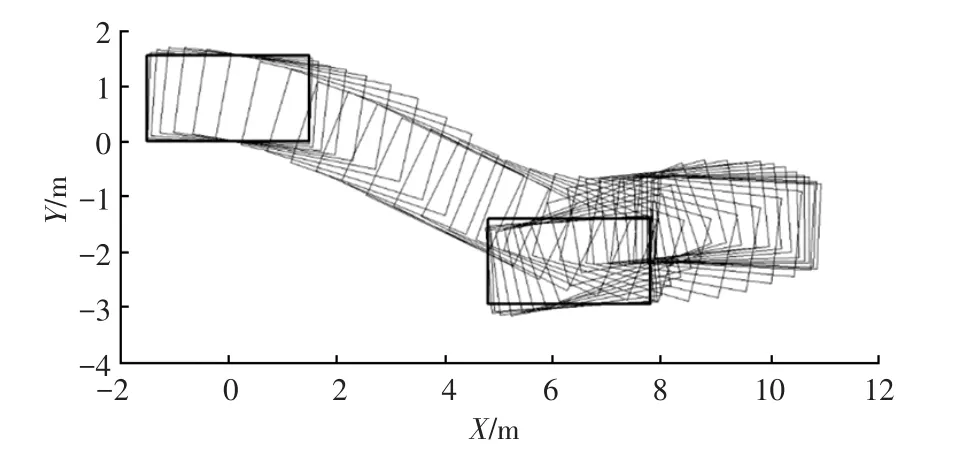
图8 汽车精细轨迹重构结果

5 结束语

本文提出的基于时域差动成像的汽车精细轨迹重构方法，通过双摄像头的可控延时启动实现了时域差动成像，解决了低成本下的毫秒级差动控制问题，克服了车辆运动带来的视场不足现象，并通过图像匹配技术计算出汽车运动参数，使用速度积分法实现了汽车精细运动轨迹的重构，所得轨迹显著优于GPS和惯导系统。同时，所研究的轨迹重构方法还能有效检测到运动过程中车体的姿态和空间占用情况，为多种车辆运动控制提供状态反馈。