对一类常考的全等三角形问题的探究

徐言飞

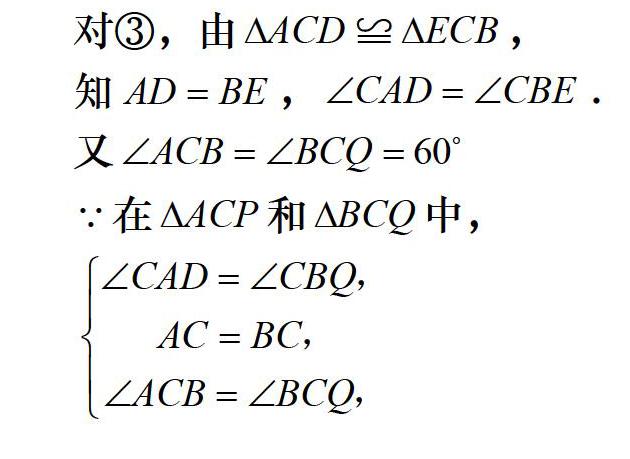
随着期中、期末、中考等大型考試命题的不断创新，试题对常见模型的考查愈加深入，越来越重视学生的知识迁移和知识创新能力.其中有一类关于全等三角形的问题颇受出题人青睐，变成了当前考试的热点.本文以一道常考的全等三角形问题为例，并进行了若干变式，期待将此类问题研究透彻.

1 试题呈现

例1 如图1，四边形ACEG和四边形BCDF是两个正方形，证明：（l）AD=BE;（2） AD⊥BE.

分析 本题意在考查正方形的性质、全等三角形的判定与性质.

解 （1）∵四边形ACEG，BCDF均为正方形，

∴AC=EC，BC=DC，

∠ACD= ∠BCE= 90°.

在AACD和AECB中，

AC=EC，

己证{∠ACD= ∠ECB，

CD= CB，

∴△ACD≌△ECB（SAS）.

∴AD=BE（全等三角形对应边相等）.

如图2，延长BE交AD于H，

∵△ACD≌△ECB，

∠l=∠2（全等三角形对应角相等）.

又△ECB是直角三角形，∠BCE=90°，

∴∠2+∠4=90°，

又∠3=∠4（对顶角相等），

∴∠1+∠3=∠2+∠4（等量代换）=90°，

∴∠DHE=90°.

∴AD⊥BE（垂直的定义）.

点评对本题第二问，还可以换一种思路，△BCE和△DHE构成“8”型，利用“8”型性质，∠1+∠DHE=∠2+∠BCE，又∠l=∠2，∴∠DHE=∠BCE=90°，则AD⊥BE.

在考试中，本题常常出现一些变式，如将正方形改为等边三角形、等腰直角三角形、顶角相等的等腰三角形，或将正方形或三角形旋转一定角度.

2 试题变式

变式1 （2015年湖北恩施中考.18）如图3，四边形ABCD，BEFG均为正方形，连接AG，CE.证明：（l）AG=CE：（2） AG⊥CE.

分析本题考查了正方形的性质、全等三角形的判定与性质、垂线的证法;熟练掌握正方形的性质，证明三角形全等是解决问题的关键.方法类似上题，第二问重点在于找“8”型.

变式2 如图4，已知点C为线段AE上一点，AABC，ACDE都是等边三角形，证明：（l） AD=BE;（2）∠AOB=60°.

分析 本题在例题的基础上变为了等边三角形，方法完全类似，意在考查学生的知识迁移能力.

变式3 若将变式2的ACDE绕点C沿逆时针方向旋转到图5时，变式2中的结论还成立吗？请说明理由.

分析 本题相对于变式2的区别在于其中的一个等边三角形逆时针旋转，沿用例题中的方法易知变式2中的结论仍然成立.

更进一步可知，这里的“沿逆时针方向旋转”换为“沿顺时针方向旋转”结论也是成立的.

变式4 如图6，AACB和AECD都是等腰直角三角形，∠ACB=∠ECD=90°，AD分别交BC，BE于点P，O，BE交CD于点Q.试猜测线段AD和BE的位置和数量关系，并说明理由.

分析 本题相对于变式3，区别在由等边三角形变成了等腰直角三角形，方法类似，发现AD=BE，AD⊥BE.

变式5 若上题中的条件“△ACB和△ECD都是等腰直角三角形”换为“△ACB和△ECD都是等腰三角形，∠ACB，∠ECD，分别为△ACB和△ECD的顶角（为锐角）且相等”，其它条件不变，试猜测线段AD和BE的位置和数量关系，并说明理由.

分析本题相对于变式3的区别在于由等边三角形变成了顶角相等的等腰三角形且顶角顶点相同，方法类似，发现AD=BE，线段AD和BE的夹角与等腰三角形△ACB的顶角∠ACB相等.注意：若△ACB和△ECD的顶角为钝角时，则线段AD和BE的夹角与等腰三角形△ACB的顶角∠ACB互补.

点评实际上不管是正方形还是三角形，图形整体运动时图形内处处保持一致.以变式2来说明△ACD≌△ECB，△ECB由△ACD旋转而来，其中CA旋转至CE，旋转了60°，CD旋转至CE，也旋转了60°.AD和CA，CD都是△ACD的组成部分，运动保持一致（角速度相同），故AD和BE的夹角为60°.

3 能力升华

在考试中，越来越注重对学生中学数学核心素养的考查.选择填空的最后一题、大题也常以例题为原型，靠近学生的最近发展区，考查学生的逻辑推理能力和知识迁移能力.我们以接下来的3道题目为例，升华一下对此类全等三角形问题的探究.

例2 如图8，点C为线段AE上的一个动点（不与端点重合），在AE同侧分别作正三角形ABC和CDE.连接AD和BE交于点O，AD交BC于P，BE交CD于Q，连接PQ.以下六个结论：①AD=BE;②PQ、/AE;③AP=BQ;④DE=DP;⑤∠AOB=60°，⑥△CPQ是等边三角形.一定成立的结论是_____________（把正确结论的序号填在横线上）

分析2008年山东菏泽市、滨州市中考第17题，2008年山东东营市中考第16题，即最后一个填空题，均考到了前5个结论.结论①⑤在变式2中己证明，现只需判断其余4个结论的正确性.

对③，由△ACD≌△ECB，

知AD=BE，∠CAD=∠CBE.

又∠ACB=∠BCQ=60°

∵在△ACP和△BCQ中，

∴△ACP≌△BCQ（ASA），

∴AP=BQ，故③成立.

对④，∵AD=BE，AP=BQ，

∴AD-AP=BE-BQ，即DP=QE.

若DE=DP，則DE=QE.

又∠CDE=60°，∴△QDE为等边三角形，与△CDE为等边三角形矛盾，故④不成立.

对②和⑥，由④知DP=QE，

由△ACD≌△ECB，

知∠PDC=∠QEC.

又∠PCD=∠QCE=60°，

∵在△PCD和△QCE中，

∴△PCD≌△QCE（AAS），

∴PC=QC.

又∠PCQ=60°，

∴△PCQ为等边三角形，

∴∠QPC=60°，

又∠BCA=60°∴PQ//AE，

故②和⑥成立.

例3在△BCD中，∠BCD<120°，分别以BC，CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF，联结AD，BE和CF交于点P.

（l）下列结论中正确的是____（只填序号即可）.①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°.

（2）求证：PB+PC+PD=BE.

分析 本题实质是变式3的推广，变为了三个等边三角形，采用相同方法可证得结论①②③成立.关键在于如何证明第二问，我们下面来进行证明.

证明在PE上截取PM=PC，连接CM，

易知△BCE≌△ACD（SAS），

∴∠1=∠2.

设CD与BE交于点G，

在ACGE和APGD中，

∵∠1=∠2，∠CGE=∠PGD，

∴∠DPG=∠ECG=60°.

（△CGE与△PGD构成“8”型）

又（l）中已证∠CPE=60°，

∴△CPM是等边三角形，

∴CP= CM，∠PMC=60°.

∴∠CPD=∠CME=∠120°.

又∠1=∠2，

∴△CPD≌△CME（AAS），

∴PD=ME.

∴BE= PB+PM+ME=PB+PC+PD.

即PB+PC+PD=BE.

例4 （2016年苏州市立达中学期末卷）在锐角三角形ABC中，AH是边BC上的高，分别以AB，AC为一边，向外作正方形ABDE和ACFG，连接CE，BG和EG，EG与HA的延长线交于点M，则①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC.其中正确的结论有（ ）个.

A.1个 B.2个 C.3个 D.4个

分析 本题实质是变式l的推广，结论①②显然成立.但本题图形比变式2复杂，线段增加了一些.难点在于判断③和④的正确性.我们下面来进行分析.

过点E作AM的高交AM的延长线于点P，过点G作AM的高交AM于点Q，△EAP与△ABH构成“K”型，AB=AE，易知△EAP≌△ABH（AAS），..，ZEAM=∠ABC，EP=AH，故结论④成立.

同理△CAH与△AQG构成“K”型，AC=AG，易知△CAH≌△AQG（AAS），∴AH=QG，∴EP=QG（等量代换），∴△EPM≌△GQM（AAS），∴EM=MG，故AM是△AEG的中线，结论③成立.所以本题中正确的结论有4个.

其实本题中还有很多等量关系，如S△EAG=S△BAC，不妨思考下：延长EA至B'，使得AB'=EA，连结GB'，∠BAC和∠GAB'都是∠CAB'的余角，∴∠BAC=∠GAB'.∵AB=EA，AB'=EA，∴AB= AB'.又AC=AG，∴△BAC≌△AB'AG（SAS）.∴S△BAC=S△B'AG，又AB'=EA，∴AG为△GEB'的中线，∴S△EAG= S△B'AG，故S△EAG=S△BAC.

4 结语

著名发展心理学皮亚杰在他的认知发展理论中指出，II岁、12岁及以后的儿童处于形式运算阶段，儿童思维发展到抽象逻辑推理水平.因此，教师尤其是数学老师在日常教学中要注重举一反三，让学生加深对知识的理解，理清知识的结构脉络与知识间的逻辑关系.

本文对全等三角形中常考的一类问题的探究，变式中的5道题目和能力升华中的3道题目都是以例题为原型产生的，不同的结论针对不同层次的学生，核心在于通过“8”型、“K”型找全等三角形，探究两条线段位置关系时，要善于转化.并要学会透过现象看本质，举一反三，锻炼自己的数学逻辑思维，掌握数学思想方法，升华自己的学习能力.