抗大规模监视密码学研究综述*
2019-07-16刘建伟张宗洋
李 耕, 刘建伟, 张宗洋,2
1.北京航空航天大学网络空间安全学院, 北京100083
2.中国科学院信息工程研究所信息安全国家重点实验室, 北京100093
1 引言
2013年6月, 美国国家安全局(National Security Agency, NSA)爆发“棱镜门” 事件, 前中央情报局职员爱德华· 斯诺登(Edward Snowden)爆料美国国家安全局和联邦调查局(Federal Bureau of Investigation, FBI)通过潜入各大网络巨头的服务器, 监控美国公民的个人信息[1].后续爆料揭露NSA一直尝试对全球通信网络进行攻击, 对世界各国重要领域的通信内容进行窃听[2].斯诺登的爆料震惊了世界, 使得人们对当前信息安全技术的可靠性产生了质疑.
“棱镜门” 及相关事件所涉及的窃密方法有部分与密码学直接相关.当前并没有公开证据表明美国情报机构能够有效破解各种常用密码体制所基于的数学难题[3], 但是却有证据显示这些机构能通过一些非正常手段攻破密码系统.例如, NSA 操纵标准化组织强行通过隐含后门的标准: Dual_EC_DRBG[4].Dual_EC_DRBG 在密码学中起着伪随机数生成器的作用, 它由NSA 内部员工设计, 跳过了形式化证明[5], NSA 通过不正当手段使其被国家标准技术研究所(National Institute of Standards and Technology, NIST)、美国国家标准学会(American National Standard Institute, ANSI)和国际标准化组织(International Organization for Standardization, ISO)等组织推荐成相关标准, 在这些标准所推荐的参数里, Dual_EC_DRBG 的设计者可以嵌入后门, 使得在获取随机数生成器足够长的输出后, 后门拥有者可以预测后续输出结果, 这就使得伪随机数生成器的安全性不复存在.Bernstein 等人[6]回顾了Dual_EC_DRBG 的设计历史和标准化过程, 解释了其后门在实际中是如何运行的, 并对NSA 所起的不光彩作用进行了深刻的揭露和批判.这种在大规模监视(mass-surveillance)的背景下, 对密码体制进行篡改和恶意设计、对算法的执行过程加入非安全因素的攻击方法跳脱了传统密码学的考虑范畴, 使得一些在传统密码学分析方法下被认为是安全的密码体制不再安全.
针对这些新问题, 抗大规模监视密码学成为密码学理论研究的一个新方向, 逐渐受到国内外学者的广泛关注.总体来说, 当前电子设备使用快速普及, 重要领域以及个人数据信息价值凸显, 各国对网络情报搜集需求上升, 密码体制应用日趋复杂化, 闭源模块与器件的广泛使用, 以及以“棱镜门” 为代表的一系列信息安全事件构成的导火索, 共同推动了这一新方向的产生.抗大规模监视密码学是传统密码学的延伸, 是密码学对新的实际情况所做的适应, 其产生和发展具有一定的合理性.
本文结合该领域当前主要成果, 对抗大规模监视密码学做了较为全面的介绍, 具体贡献如下:
(1)提炼了抗大规模监视密码学的一般特征, 总结了诸如IV 替换攻击、偏密文攻击、输入触发攻击等各种攻击方法, 基于监视-检测、watchdog 等安全模型, 以及分割-融合、自防御、密码反向防火墙等各种安全防御方法;
(2)从单向函数、伪随机数生成器、加密体制、签名体制、密码协议等方面介绍了该领域主要结论及相关最新进展, 理清了发展脉络, 并对研究动向做了一定的展望.
本文组织结构如下: 第2 节介绍了抗大规模监视密码学的基本特征与当前研究布局; 第3 节介绍了抗大规模监视的加密和签名体制研究; 第4 节介绍了抗大规模监视的密码学原语研究; 第5 节介绍了抗大规模监视的密码协议研究; 第6 节介绍了抗大规模监视密码学其他研究方向; 第7 节对当前抗大规模监视密码学的研究工作做了总结和展望.
2 抗大规模监视密码学基本特征与研究布局
传统密码学针对密码体制的安全性分析, 一般默认目标算法能够正确地被执行, 在此基础上进行形式化分析.然而在大规模监视密码学中, 为了更准确地反映实际情况, 不再无条件保证算法的正确执行, 将密码算法的执行阶段视作博弈的一个环节.这是因为实际中大量的密码相关单元属于闭源模块.另外, 由于密码算法的复杂度日益增大, 通过代码本身来分析算法安全性的难度也迅速增大(例如心脏滴血漏洞在程序源代码公开近两年后才被发现[7]).安全防御一方仅能通过分析算法的输入与输出判断其执行的正确性.
Schneier 等人[8]在分析恶意弱化密码体制的行为时, 将新环境下各个实体概括如下:
(1)破坏者(Saboteur): 通过恶意篡改等各种方式对密码体制本身进行弱化的一方;
(2)受害者(Victim): 被弱化的密码体制的使用者;
(3)攻击者(Attacker): 试图利用弱点攻击受害者的一方;
(4)防御者(Defender): 基于安全目的设计密码体制的一方.
这种概括在一定程度上可以代表大规模监视背景下围绕密码体制的博弈形式.
由于上述基础假设的变更, 抗大规模监视密码学与传统密码学在安全性的定义上产生了分歧.在大规模监视密码学中出现了诸如算法替换攻击、参数替换攻击等一系列新型攻击方式.密码学体系的各个组成部分, 如密码学原语(单向函数、伪随机数生成器等)、加密、数字签名和密码协议等等, 其安全性需要重新进行分析.面对新的威胁, 一方面, 可以对这些密码学构件重新设计, 如采用分割-融合技术等对密码算法进行重新设计, 以保证在新威胁下的安全性; 另一方面, 也有部分研究提出引入一些新的方式和机制, 如密码反向防火墙等, 保证密码体制的安全性.鉴于抗大规模监视背景下, 攻击与防御的形式和方式更为复杂, 如何对实际情况进行抽象, 总结出合理的形式化安全模型, 用以分析上述所有攻击和防御方法的有效性, 也是该领域当前核心研究内容之一.以上内容构成了抗大规模监视密码学总体研究布局, 如图1 所示.
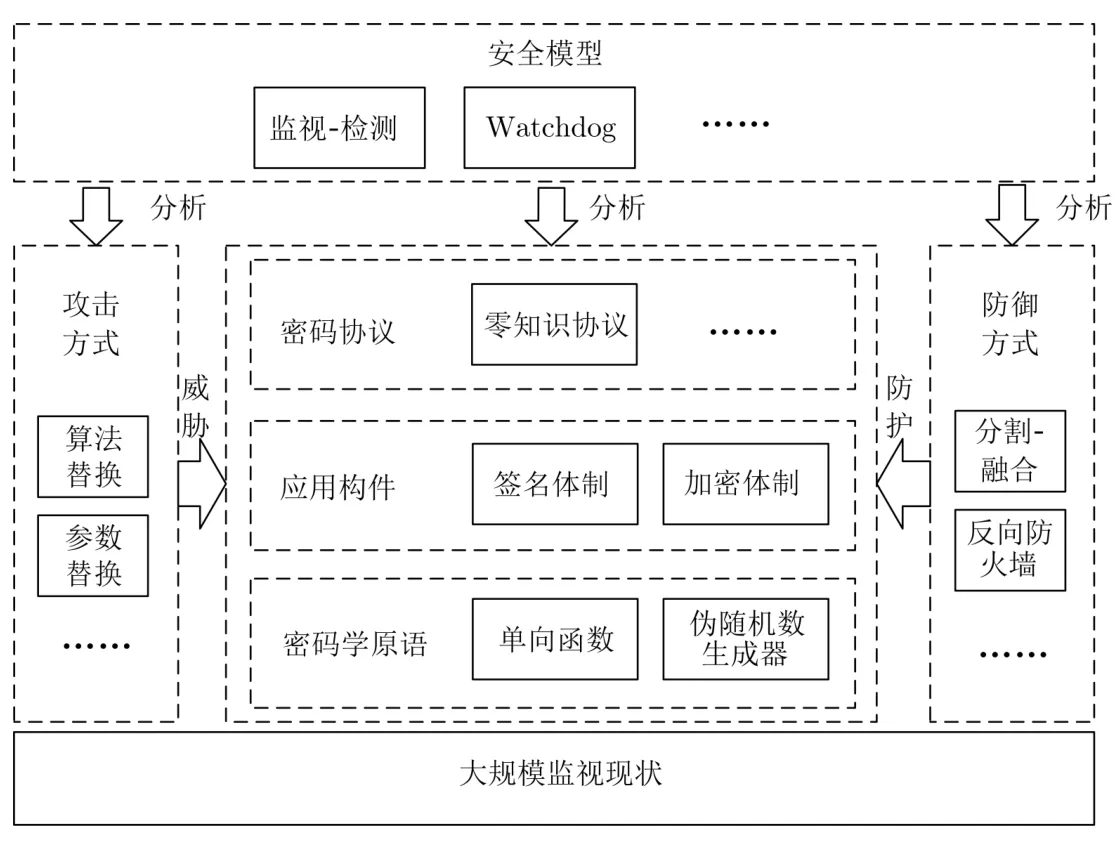
图1 抗大规模监视密码学Figure 1 Cryptography against mass surveillance
3 抗大规模监视加密和签名体制研究
相关方面的研究最早可追溯到1983年, Simons[9]指出恶意修改密码体制的实现方式会弱化其安全性.攻击者在密码体制中, 利用公钥加密、数字签名等密码技术建立起一种隐蔽信道, 除指定接收者外, 其他人都无从知晓通信信息是否嵌入隐藏消息.按着这一思路发展, Young 等人[10–13], Bellare 等人[14]分别从攻击方法、防御方法和安全模型等方面对大规模监视下的加密和签名体制展开了一系列研究.
3.1 攻击方法研究
攻击方法的研究对整个研究体系的建立起着重要的牵引作用.目前在抗大规模监视背景下, 算法替换攻击(algorithm subversion attacks, ASAs)是攻击加密体制的重要手段之一.ASAs 指攻击者使用自身特有的权力和能力, 使用某种经过篡改的算法去替换被攻击者使用的纯净算法, 并结合各种后续具体方法,达到获取信息的目的.以下是迄今为止提出的几种主要的具体攻击方式, 总结见表1.
SETUP:Young 等人[15]于1996年针对黑盒密码体制提出了一种名为通用保护的内嵌后门(secretly embedded trapdoor with universal protection, SETUP)的攻击机制.其主要攻击思路基于公钥密码体制, 由攻击者设计替换算法C′, 用以代替用户器件中的纯净密码算法C, C′中含有一个公钥, 而窃取秘密的攻击者持有此公钥所对应的私钥(为表述方便, 此处将之称作后门信息).C′与C 在不掌握后门信息的使用者看来具有相同的输入输出特征, 在概率多项式时间内计算上无法区分.但是攻击者可以使用后门信息, 通过C′所产生的输出获取相应敏感信息, 如使用者的明文、密钥等等.此过程具有一定反追溯性.Young 等人根据强度的不同定义了强SETUP 和弱SETUP, 并将这种对密码体制进行攻击和安全分析的思路概括为kleptography.在该框架下, Young 等人针对常用密码体制, 包括Diffie-Hellman 密钥协商体制[16]、RSA 加密体制、ElGamal 加密体制[17]、ElGamal 签名体制和Kerberos 协议[18]等, 设计了一系列具体攻击方法[10–13].
Teseleanu[19]在SETUP 机制中引入了门限体制, 提出了针对ElGamal 签名体制的(ℓ,n)-门限SETUP 攻击方案.其中, n 个恶意实体中如有ℓ 个参与攻击, 则可获取受害者的相应私钥.此种攻击方式更有利于保护攻击者的身份.
IV 替换攻击(IV-replacement attack):此攻击由Bellare 等人[14]针对对称密码体制提出.攻击者对密码算法进行恶意颠覆, 其与颠覆算法之间享有一个密钥(称颠覆密钥), 颠覆后的密码算法在实现过程中, 将本应具有随机性的初始向量IV, 由对用户密钥加密所得密文代替, 此过程加密密钥为颠覆密钥.当存在有效算法利用密文恢复IV 时, 攻击者可以使用所掌握的颠覆密钥对IV 进行解密获取用户密钥.
偏密文攻击(Biased-ciphertext attack):此攻击由Bellare 等人[14]提出, 适用于随机化加密体制.被颠覆的加密算法在某一明文所对应的密文集合中, 带有特定偏向性而非随机均匀选取密文, 通过这种偏向性将加密密钥逐比特按序泄露.掌握后门(颠覆密钥)的攻击者能够识别这种偏向性, 获取关键信息, 并攻破加密体制; 而不掌握后门的用户则无法识别此偏向性.偏密文攻击是一种强大的攻击方式, 理论上对所有随机化、无状态、随机数单射(coin injective)1随机数单射(coin injective): 对所有密钥、消息以及关联数据, 加密过程中所使用的随机数到密文的映射是单射.的对称加密体制都具有有效性.
改进的偏密文攻击:Bellare 等人[20]提出了改进的偏密文攻击方式.之前的偏密文攻击需要逐比特按序泄露密钥, 因此颠覆算法必须是有状态的; 改进的攻击方式则实现了一次密文泄露密钥一个随机的比特位, 这样颠覆算法本身可以具有无状态的特性, 攻击适用范围更广.
输入触发颠覆(Input-triggered subversions)攻击:Degabriele 等人[21]针对文献[14]所提出的安全分析模型(详见3.2节)的局限性, 提出了输入触发颠覆攻击, 即颠覆算法仅在输入为特定信息时才采取一定机制泄露密钥等关键信息, 其余情况下均执行与纯净算法一样的操作, 且此特定信息仅有攻击者知晓.简言之, 即颠覆算法在仅由攻击者掌握的特定的输入下才发动攻击.
定时炸弹(Time bombs)攻击:文献[22]和文献[23]分别讨论了木马与硬件后门中的定时炸弹攻击.该攻击与输入触发替换攻击在思路上相类似, 只是触发攻击的因素是特定时间, 可逃避离线看门狗(offline watchdog)(详见3.2节)的审查.
偏随机数攻击(Biased randomness attack):该攻击由Ateniese 等人[24]针对签名体制提出, 基本构造思路与偏密文攻击类似, 在随机化签名体制中, 颠覆算法使用一个伪随机函数以及与攻击者共享的颠覆密钥, 偏向性地选择签名所用的随机数, 实现每一次签名泄露签名者私钥的一个比特.攻击者在获取若干签名后, 可以恢复出签名密钥.
非对称颠覆攻击(Asymmetric subversion attacks):Liu 等人[25]针对当前一系列常用的签名体制设计了非对称颠覆攻击.该方法具有反追溯特性, 监视者所掌握的后门并不嵌入颠覆算法中.
此外, Auerbach 等人[26]还针对加密体制提出了参数颠覆攻击(parameter substitute attack, PSA)方法, 详细将在6.2 节中介绍.

表1 主要ASAs 方式总结Table 1 Summary of ASAs
3.2 抗大规模监视安全模型研究
安全模型研究是抗大规模监视加密和签名体制研究的主线之一.其主要针对新背景下的现实情况, 包括攻击方与防御方所能掌握的信息、影响的环节等, 以形式化的语言, 设计相应游戏, 建立起大规模监视背景下对密码体制进行安全性分析的标准.抗大规模监视下密码学的安全模型相比于传统模型如CPA 模型、CCA 模型等[27–29]有较大的发展.
Young 等人[12,13]在对SETUP 具体攻击方式进行广泛探索后, 明确定义了基于游戏的SETUP 攻击,并将算法执行可颠覆的密码学称为kleptography.Bellare 等人[14]第一次对大规模监视下的算法替换攻击作出了一系列形式化定义, 首次建立了基于监视-检测的安全模型思路, 提出了针对ASAs 的较为完整的安全模型(BPR14), 并对攻击与防御方法的有效性给出了形式化判断方法.BPR14 模型的基本思路为, 在ASAs 环境下, 攻击者一方面需要保证攻击的有用性, 即能够从所设计的颠覆算法产生的密文中得到敏感信息; 另一方面, 需要保证攻击的隐蔽性, 即不掌握后门信息的普通用户无法觉察到攻击的存在, 否则攻击理论上无法持续下去.基于这种思想, Bellare 等人设计了代表攻击方执行的监视游戏(surveillance game), 与代表防御方(用户, 密码体制设计者)执行的检测游戏(detection game), 在游戏的基础上定义了刻画某种替换算法(攻击方法)的抗检测性与刻画某种密钥体制的抗监视性.
然而, BPR14 模型存在一定局限性.为了保证内部逻辑的严谨, BPR14 模型对所分析的颠覆算法做了严格的限制, 要求颠覆的加密算法与纯净的解密算法之间能满足完美的加解密正确性.Degabriele 等人[21]对这种限制提出了质疑, 并通过设计输入触发颠覆攻击, 否定了原模型在放宽对颠覆算法的限制时的实用性.他们针对BPR14 模型的局限提出了改进的安全模型(DFP15).DFP15 模型适用于分析范围更广的颠覆算法, 其关注的是一个在线过程, 即检测者并不意在判断密码体制是否被颠覆, 而关注攻击者是否通过颠覆达到了获取了相应信息的目的.该模型将检测游戏设计为检测方审阅监视游戏的在线交互记录, 从而体现出监视与检测是一对针对同一对象、基于不同目的的竞争过程, 通过双方的优势对比来定义密码体制的抗颠覆性.
DFP15 模型虽然具有更大的适用范围和更完备的内部逻辑, 但其与现实情况的符合程度值得商榷.Bellare 等人[20]提出了新的安全模型(BJK17), 相较于之前模型, 此安全模型主要特点在于, 检测方的能力更强, 在询问中可以自主提交密钥, 并可获取算法的更新状态σ; 并对攻击者提出了更高的要求, 监视游戏最终提交的不是一个判断比特b, 而是完整的用户密钥.此模型是在Degabriele 等人的质疑下对安全模型发展所做的又一次改进.
数字签名在身份认证、数据完整性、不可否认性以及匿名性等信息安全领域中有着重要的作用[30].Ateniese 等人[24]在算法替换背景下, 对签名体制的安全性做了相对完整的研究, 指出一大类随机化数字签名方案不能避免替换攻击.对抗ASAs 的签名体制的研究在一定程度上借鉴了上述加密体制的研究思路, 并结合了数字签名的特点以及其传统形式化安全定义方式.出于在ASAs 下对数字签名体制分析的需要,定义了签名体制的唯一签名性(unique signatures)、正确性(correctness)、可验证性(verifiability)、宽松可验证性(relaxed verifiability)等具体性质.在新环境, 即存在算法替换者和攻击者的情况下, Ateniese等人设计了针对原体制代表攻击者参加的不可识别性游戏、针对颠覆体制代表使用者或监管方参加的公共/私有不可检测性游戏、针对颠覆体制代表攻击者参加的选择明文攻击下的冒充性游戏.以上工作所建立的形式化分析模型是分析抗ASAs 的数字签名体制安全性的依据.
Russell 等人[31]提出了基于看门狗(watchdog)的安全模型, 基本思想为基于检测的安全.该模型引入一个正面第三方(实际中可视为网络管理者), 将所有的检测能力集成为一个身份——看门狗(watchdog).模型由看门狗、敌手与挑战者(用户)之间的三方交互规则来定义, 三者之间交互方式如图2 所示.根据权限的不同, 看门狗被分为离线看门狗(offline watchdog)、在线看门狗(online watchdog)、以及全知看门狗(omniscient watchdog)三类.看门狗可获取标准算法(纯净算法)与被视为黑盒的实际运行算法; 此外, 在线看门狗和全知看门狗还可以获取敌手与挑战者之间运行游戏的在线交互副本, 全知看门狗甚至可获取挑战者的私有状态.另外, 敌手与挑战者之间运行传统的安全游戏.针对一个密码体制, 如果所有的颠覆攻击, 要么无法削弱安全性, 要么能大概率地被看门狗检测出来, 则称这样的密码体制是安全的.该模型理论上可分析所有kleptography 环境下的密码算法安全性.

图2 Watchdog 防御模型Figure 2 Defense system based on watchdog
Horel 等人[32]提出了一种较为特殊的安全模型, 其中挑战者必须使用敌手所提供的加密算法, 而且敌手有能力解密此算法产生的密文.挑战者可以采取特殊的调用方式, 以期在通信双方之间建立一条隐蔽信道, 而使得敌手无法通过所传输的信息判断通信双方是否在信道中隐藏了秘密信息.该安全模型与隐写体制有很大相似, 但严格意义上来讲存在明确的区别.主要区别在于, 其一, 双方事先没有共享秘密信息;其二, 双方无法自主选择明文.
笔者[33]考察了现实中存在多个独立监视者的场景并定义了一种新的安全模型, 在该场景中, 用户只能使用监视者提供的算法来构建密码系统并传递消息, 但是这些算法可以来自多个不同的监视者, 并且这些监视者之间相互独立.如果所有的监视者, 要么认为用户诚实地执行了其给出的颠覆算法(对用户之间真实消息的传递毫无察觉), 要么认为用户执行的是未经颠覆的纯净算法, 则称该系统是安全的.
以上是当前对于抗大规模监视背景下建立的安全模型所做的主要探索.相关研究在一定程度上形成了大规模监视背景下, 密码设备本身不可信时分析算法安全性的研究思路, 为后续具体的密码体制研究提供了框架.然而, 由于新背景下攻击的形式, 以及攻击方的权力和能力等情况极其复杂, 现有模型与实际情况的吻合度值得商榷, 尚未有一种公认模型能够完美地刻画现实环境, 相关研究仍在继续中.
3.3 大规模监视防御方法研究
对抗颠覆攻击的一种较为直观的防御方法是在一个密码体制的实现中采用多个不同来源的设备.此时攻击者只有在同一时间颠覆所有设备才能成功获取敏感信息.但此种方法显然带来了额外的成本开销.
偏密文攻击(详见3.1 节)的提出, 从理论上证明了在没有进一步防护机制(如外加可信设备等)的情况下, 所有随机化加密体制(有状态、无状态)都不能抵抗ASAs.因此, 如果从算法本身的层面上来进行安全防护, 则所设计的加密体制必须满足唯一密文(unique ciphertext)的性质, 即在纯净的解密算法下,任一明文所对应的密文集合的元素个数不大于1.文献[14,20,21,34]等都通过严格的数学方法, 证明了在各自所提出的安全模型下, 唯一密文体制具有抗颠覆的性质.
在签名体制防护方面, Ateniese 等人[24]证明了满足唯一签名性等特定性质的签名体制, 在攻击者所使用颠覆体制具有一定限制(如保留正常功能)的情况下, 具有不可识别性.这为设计在ASAs 下安全的数字签名体制提供了方向性的建议.另外, 他们还将密码反向防火墙(CRF)的概念应用于签名体制, 定义了带CRF 的安全模型, 并给出了具体构造.Chow 等人[35]结合watchdog 模型与分割-融合(decomposition and amalgamation)技术(详见下段)对签名体制提出了一种通用性的颠覆防御方法; 并引入全域哈希, 设计了完全颠覆模型下安全的签名体制.另外, 在攻击者能力有限的情况下, 门限签名对于ASAs 具有较强的防护能力, 至少目前尚没有文献提出对于门限签名体制的此类攻击方案[19].
Russell 等人[36]对随机化密码算法提出了一种防御方法.此方法基于分割-融合(decomposition and amalgamation)技术.此技术将密码算法进行分割, 分割后的算法一部分为随机性算法RG, 如随机字符串生成算法、密钥生成算法等, 另一部分为确定性算法DG.所有的算法构件重新组合后能够实现与原算法相同的功能.分割后的算法都能够被广泛测试.由于DG 的确定性的性质, 使得攻击者只能对RG 进行攻击.为了使针对RG 的后门不产生作用, 此模型又将所有RG 进一步分割为两个相互独立的随机算法和一个基于随机预言的可信整合算法, 以此达到防护密码体制的目的.
以上对加密和签名等密码体制的分析, 都需要一定程度地限制攻击者所使用的颠覆算法.然而, 在防御方(检测者)能力较弱时, 不排除存在颠覆算法无限制的ASAs, 这种攻击的危害则更为直接.基于密码协议的分析框架, Mironov 等人[37]首次引入密码反向防火墙(cryptographic reverse firewall, CRF)的概念.CRF 是部署于信息系统与外部之间的安全模块, 区别于传统的抵抗外来攻击的防火墙概念, CRF存在的目的是为了防御由内部攻击所造成的对外泄露关键信息的安全威胁.CRF 具有特殊的信任状态,一方面其具有执行的可信性, 即不可颠覆性; 另一方面, 其身份本身又具有不可信性, 即仅允许其掌握原本可公开的数据, 如公钥、密文等等.Mironov 等人沿用传统的密码协议形式化框架, 给出了CRF 运行方式的形式化定义, 即协议中每个实体对外发送与接收的信息均经过CRF 的处理(如图3 所示).CRF 需要满足以下三个基本性质:
(1)功能保留性(Functionality–maintaining): 引入CRF 后仍保留原协议的功能;
(2)安全保留性(Security-preserving): 引入CRF 后仍保留原协议的安全性;
(3)抗泄露性(Exfiltration-resistance): 引入CRF 后, 任何内部攻击无法对外泄露额外信息.

图3 CRF 运行示意图Figure 3 Operation of CRF
CRF 的安全保留性与抗泄露性有着紧密的关联, 但二者互不蕴含.笔者[38]对其二者在消息传输协议框架下的相互关系进行了详细的形式化分析, 并对Mironov 等人提出的CRF 抗泄露性定义做了一定程度的完善, 考虑了游戏定义中敌手能力更强的情况.
Fischlin 等人[39]提出了自防御密码协议的防御方法, 它区别于密码反向防火墙与基于检测的看门狗(watchdog)的防御机制.该类体制假设存在“安全锚(security anchor)”, 以确保一个安全的启动阶段2在安全的启动阶段中, 使用者可获取算法的一个纯净版本..当把部分密码算法建模成可颠覆黑盒时, 基于安全启动阶段, 特殊设计的密码协议可以使得攻击者的优势可忽略.根据这一思路, Fischlin 等人为具有同态性质的公钥加密体制和随机化单钥加密体制设计了相应安全防护方法.
4 抗大规模监视密码学原语研究
4.1 颠覆环境下的单向函数及哈希函数研究
作为密码学基本原语之一, 单向函数对密码体制的构建起着重要的作用.Russell 等人[31]构造了一个在传统模型下安全, 但无法抵抗kleptography 环境下攻击的单向函数实例, 指出在新情况下有必要重新分析单向函数的安全性并给出构造.Russell 等人在其所定义的watchdog 模型(详见3.2 节)下, 定义了单向置换(one-way permutation, OWP)的三种安全性质, 分别为: (1)OWPC, 敌手可以选择OWP 的参数生成函数; (2)OWPA, 敌手可以直接提供OWP 的公共参数; (3)OWPSP, 其定义基于分离程序模型(split program model).在合适哈希函数假设下, Russell 等人给出了利用传统OWP 构造满足OWPA和OWPSP安全的OWP 的方法.
Russell 等人[40]在kleptography 环境下形式化分析了随机喻言机的安全性, 对被颠覆的随机喻言提出了纠正方法, 使得在颠覆攻击下仍然能够可信地黑盒调用随机喻言, 而无需关心随机喻言的具体实现.当哈希函数被颠覆时, 通过对一系列哈希输出值进行异或, 并再次运行哈希函数的方法, 利用颠覆算法仍需要满足黑盒测试下无法被检测识别的限制, 可以实现最终的输出能够满足随机喻言下的安全要求.Russell 等人在无差别(indifferentiability)模型下证明了纠正方法的安全性.
4.2 带有后门的伪随机数生成器研究
伪随机数生成器(pseudorandom number generator, PRG)在密码体制中扮演着十分重要的角色, 其本身的安全性对于密码体制的安全起着十分重要的作用[41].
在抗大规模监视密码学产生之前, 就有包括Barak 等人[42]在内的学者对PRG 的安全性进行了形式化定义.受斯诺登事件的影响以及文献[14]等对算法替换攻击形式化分析思路的启发, 研究人员还严格分析了一系列PRG 相关标准[43–46], 并开始研究在内部攻击安全威胁下的带有后门的伪随机生成器(backdoored pseudorandom generators, BPRG).
Dodis 等人[47]形式化定义了BPRG 的安全性质.其在传统的PRG 安全性定义的基础上, 加入了后门信息sk 并允许攻击者掌握sk.BPRG 的定义基于两个游戏: 挑战者与普通敌手A(不持有后门信息sk)的游戏, 和挑战者与持有后门信息sk 的敌手B 的游戏.BPRG 需要在第一个游戏中表现出传统PRG的安全性质, 并在第二个游戏中使敌手B 可以凭借后门sk 获取特殊的优势.根据敌手B 可获取的不同特殊优势, 可以将BPRG 的强度分为3 类:
(1)敌手可以区分BPRG 的多步输出和等长的均匀随机分布字符串.
(2)敌手可以根据BPRG 的多步输出恢复出BPRG 的最后状态.
(3)敌手可以根据BPRG 的多步输出中任意一步输出恢复出其余任意一步输出.
Dodis 等人给出了BPRG 的构造方法, 并通过BPRG 与公钥密码体制之间的相互构造证明了其二者之间等价.Dodis 等人还研究了对BPRG 的免疫方法, 讨论了使用一种作用于BPRG 输出端的“非平凡函数” 来保证输出结果对于敌手B 的随机性的方法, 由此定义了公共免疫、半私有免疫、以及私有免疫三种免疫的强度, 证明了公共免疫的不可能性, 并给出了后两种免疫的具体方法.
Degabriele 等人[48]在Dodis 等人工作的基础上, 给出了两种新的BPRG 安全性定义.新安全性定义对敌手B 的要求更高, 要求其在得到单步输出后可以恢复BPRG 的状态以及BPRG 的所有可能输出.随后, 他们考察了带输入的伪随机数生成器(pseudorandom number generator with input, PRNG with input)模型[42], 研究其存在后门(backdoored PRNGs with input, BPRNG with input)时的形式化定义, 规定敌手可以获取泄露的输入信息、获取或设置BPRNG 的状态并在其输入累计熵达到一定值后获取挑战消息.Degabriele 等人基于可再随机化加密体制[49]具体构造了带输入的BPRNG, 并给出了BPRNG 状态长度与攻击者成功嵌入后门机会之间的关系.
Russell 等人[31]基于经典的Blum-Micali PRG 构造方法[50]和OWPA(详见4.1 节), 设计了抗颠覆攻击的PRG.考虑到Dodis 等人已给出的相关否定结论, 即不可能通过将“非平凡函数”作用于BPRG的输出实现BPRG 公共免疫, Russell 等人则采取不同思路绕开了这一点, 其设计基于对PRG 公共参数的随机化处理.
5 抗大规模监视密码协议研究
5.1 零知识协议相关研究
在交互式证明协议中, 如果恶意的验证者只知道输入命题正确与否, 却获取不到其他一切有用信息,则称此协议为零知识协议[51].Ben-Sasson 等人[52]分析了零知识协议中共同参考字符串(common reference string, CRS)被颠覆时的安全威胁, 提出了分布式CRS 生成方案, 使得只要其中一个实体诚实,则协议安全.Bellare 等人[53]分析了恶意共同参考字符串模型下非交互式零知识(non-interactive zeroknowledge,NIZK)协议[54]和非交互式证据不可区分(non-interactive witness indistinguishable,NIWI)协议的安全性, 形式化定义了颠覆可靠性、颠覆不可区分和颠覆零知识性质, 并考察这三种性质与传统可靠性、不可区分性和零知识性的各种组合性质, 给出一系列肯定或者否定结果.针对NP 语言, 主要结果包括4 点:
(1)在文献[55]所提供范例的基础上, 通过构造能破坏可靠性的模拟者, 证明了不存在颠覆可靠的NIZK;
(2)通过借助NP 关系与双线性群生成器构造的NIZK 框架, 基于computational Diffie-Hellman(CDH)、decision linear (DLin)和knowledge-of-exponent (KEA)变种假设, 证明了存在满足颠覆零知识的NIZK;
(3)借助于文献[56]构造的非交互式系统, 基于DLin 假设, 证明了存在颠覆可靠和颠覆不可区分的NIWI;
(4)借助伪随机数生成器和ZAP (即两轮的NIWI 协议[57])构造的NIZK, 证明了存在颠覆不可区分的NIWI 协议.
Abdolmaleki 等人[58]在文献[53]的基础上, 要求CRS 陷门可提取以及CRS 公共可验证, 实现了计算可靠和完美可组合的抗颠覆零知识系统.
5.2 基于密码反向防火墙的抗大规模监视安全协议
密码反向防火墙(CRF)是部署于信息系统和外部之间, 防止因内部攻击造成对外信息泄露的器件(详见3.3 节).在密码协议中, CRF 通过对协议中传输的信息实施“再随机化” 以及其他相应操作, 实现在保留原协议功能和安全要求的基础上, 防止被颠覆的实体对外泄露信息.
Mironov 等人[37]针对由Naor 等人[59]、Aiello 等人[60]各自独立提出的基于DDH 难题的不经意传输协议, 为协议双方都设计了CRF.所设计的CRF 基于内部生成的随机数, 在满足原协议功能的前提下对消息收发双方发出的消息都进行了再随机化.可以证明即使在协议实体遭到颠覆的情况下, 经随机化后的消息仍然可以与完全随机均匀产生的消息不可区分.Mironov 等人还给出了一种方法, 能够将任意协议转化成一个实现相同功能的新协议, 在新协议中所有实体都可以配备一个具有强抗泄露性(详见3.3 节)的CRF, 以此来保护实体在颠覆风险下的安全性.
Dodis 等人[61]在文献[37]建立的框架下, 继续定义了CRF 可检测失败(detectable failure)的性质, 并对消息传输协议环境下的CRF 进行了较为全面的研究.针对消息传输协议, 他们借助于再随机化加密体制, 提出了协议双方的CRF 的通用构造方法.并且, 他们构造了一种抗选择密文攻击的安全密钥协商协议的CRF.
国内学者陈等人[62]在平滑映射哈希系统[63,64]的基础上, 通过引入密钥可延展性和元素可再随机化性, 提出了可延展平滑映射哈希系统的概念, 并给出了一个相应实例.基于可延展平滑映射哈希系统, 他们为包括消息传输协议、不经意信封协议、不经意传输协议在内的多种协议构造了CRF.
6 抗大规模监视密码学研究其他方向
6.1 算法替换攻击与隐写体制相关研究
算法替换攻击的思想与隐写体制(steganography)联系紧密.Berndt 等人[65]重新分析了现有算法替换攻击的本质, 认为针对对称加密体制的颠覆其本质就是构造一种隐写体制.他们对对称加密算法的颠覆体制与隐写体制实现相互构造, 严格证明了其二者实际上是等价的, 这也为设计算法替换攻击提供了一种实际可行的方法.Russell 等人[36]从隐写的角度讨论了针对随机化加密体制的抗颠覆防御方法, 提出了无隐写(stego-free)体制的概念.
6.2 参数颠覆攻击相关研究
参数颠覆的概念首次由Bellare 等人[53]提出.他们分析了非交互式零知识协议在共同参考字符串在遭到恶意颠覆时的安全性(详见5.1 节).另外Dodis 等人[47]和Degabriele 等人[48]在研究伪随机数生成器时也采用了参数颠覆的思想(详见4.2 节).文献[66–69]分别考察了公共参数在非可信环境下生成时密码体制的安全性.
Auerbach 等人[26]在参数颠覆攻击下形式化定义了公钥加密体制和密钥封装体制的安全模型, 其中,敌手可以完全控制公共参数的生成过程.他们提出了相较于传统密文不可识别性、公钥隐藏性更强的密文伪随机性(ciphertext pseudo-randomness, CPR)的概念, 以及高效可嵌入群族(efficiently-embeddable group, EEG)概念, 构造了具有CPR 性质的密钥封装体制, 又基于椭圆曲线密码学, 给出了EEG 实例的构造方法.
6.3 抗泄露密码学相关研究
抗算法替换攻击、抗公开参数替换攻击等攻击的密码体制并不能够保证一定可避免其他潜在攻击.在当前背景下, 攻击的手段日趋多样, 如侧信道攻击就是一种强大攻击方法.侧信道攻击指当加载密码体制的电子设备运行时, 通过测量其运行过程中的时间消耗、功率消耗或电磁辐射等侧信道信息, 进而获取密钥部分或全部信息.针对于此, Dziembowski 等人[70]正式提出了抗泄露密码学(leakage-resilient cryptography), 抗泄露密码学将物理泄漏方式抽象为信息论意义上的泄漏函数, 在此基础上设计可证明安全的密码算法和协议, 使得算法和协议的安全性独立于底层的硬件实现工艺和敌手的侧信道攻击手段, 因此具有更广的安全性.当前, 研究人员已设计了抗泄露攻击的单向函数[71]、伪随机函数[72,73]、对称加密体制[74,75]、公钥加密体制[76–79]、消息认证码[74,75]和零知识证明协议[80,81]等.笔者在抗泄露的公钥加密领域进行了相关研究, 利用零知识协议构造了后挑战泄露情况下选择密文攻击安全的公钥加密体制[82].
抗泄露密码学与抗大规模监视密码学有着紧密的关联, 在产生背景、前提假设、关注对象、分析方法等方面存在广泛的共通性.在某些情况下, 二者所产生的密码体制也具有相互借鉴意义, 二者研究存在着结合的趋势.
7 展望与结束语
从目前学术界的研究来看, 抗大规模监视密码学实际上是在新背景下对传统密码学所做的一种推进和延伸.结合学者们在各方面所做工作, 此领域研究现已完成了从发现问题(设计攻击方法)、定义问题(建立安全模型等)到解决问题(设计防御体制)的一个较为完整的框架, 然而仍存在诸多不足之处, 很多现实问题未能得到很好的解决, 主要包括:
(1)现有抗大规模监视安全模型与现实情况存在偏差.迄今为止发表的公开文献中, 对于抗大规模监视的威胁的建模各有优缺点, 但核心思想都较为相似, 且都不能十分全面地刻画现实情况.
(2)现有的防御策略在实际中较难实现.当前所设计的针对大规模监视的防御策略, 一方面集中在放弃随机化体制, 回归确定性加密, 这显然无法满足相当大一部分现实需求; 另一方面则使用CRF、分割-融合技术、可靠伪随机数生成器等方法保证随机化密码算法的安全, 这些方法都需要较强的假设或较高的实现成本.
如何解决上述问题将是此领域下一步的重要研究方向.本文介绍了当前在该领域各个方面的主要研究成果.由于实际所面对问题的复杂性, 抗大规模监视密码学的发展也是一个曲折的过程, 此方面的研究目前还处在一个较为初步的阶段.抗大规模监视密码学的研究对于突破与丰富当前密码学理论, 探索新的密码应用技术, 解决新形势下现实信息安全问题, 都具有重要的理论和现实意义.
