轻量级分组密码GIFT 的差分故障攻击*

2019-07-16冯天耀韦永壮史佳利郑彦斌

密码学报 2019年3期

关键词：密文差分密钥

冯天耀, 韦永壮, 史佳利, 丛旌, 郑彦斌

1.桂林电子科技大学广西密码学与信息安全重点实验室, 桂林541004

2.桂林电子科技大学广西无线宽带通信与信号处理重点实验室, 桂林541004

3.桂林电子科技大学广西高校云计算与复杂系统重点实验室, 桂林541004

1 引言

物联网设备通常受到存储资源、运算资源、能耗资源等限制, 不能运行高强度的密码算法和协议.从而, 轻量级算法和协议应运而生[1–13], 旨在保证设备安全性的同时, 节省资源的消耗.目前国内外陆续提了许多轻量级密码算法, 如GIFT[4]、PRESENT[5]、MIDORI[6]、PRINCE[7]、LBLOCK[8]、LED[9]、MIBS[10]、TWINE[11]等.其中GIFT 算法是Subhadeep Banik 等人于2017年提出的一种轻量级密码算法[4], 其分组长度支持64 比特或128 比特, 密钥长度为128 比特, 轮数分别为28 轮或40 轮.GIFT 密码算法是PRESENT 算法的一种改进算法, 不但节省了大量的资源消耗, 还提高了运行速度, 与此同时还改进了PRESENT 算法线性层的脆弱部分.GIFT 算法设计简单, 在资源消耗方面甚至优于SIMON[12]、SKINNY[13]等算法, 成为当前最具实现效率的算法之一.

1997年Biham 和Shamir 针对DES 密码算法提出了差分故障攻击[14], 其核心思想是在密码设备正常运行时通过外部物理攻击得到错误密文, 运用差分攻击的原理, 结合错误密文与正确密文获取密钥.关于差分故障攻击的研究已经成为密码学研究热点之一.目前, 差分故障攻击已经应用到一些轻量级密码算法的分析中, 如MIDORI[15]、PRIDE[16]、PRESENT[17,18]等.以PRESENT 算法为例, 文献[17]能够通过在非线性层注入18 个单比特故障恢复全部密钥比特.文献[15]能够通过注入3 次随机半字节、2次随机字节故障, 分别获取Midori64、Midori128 的密钥信息.但是, 关于GIFT 算法能否抵抗差分故障攻击, 目前没有相关的研究进展.

本文通过利用GIFT 算法的内部结构提出了两种通用、有效的差分故障攻击方法.其核心思想是在S盒运算前注入错误故障, 利用差分密码分析的基本原理, 分析错误故障导致的S 盒输入差分与输出差分,进而获取内部状态的信息.针对GIFT 算法的轮结构, 根据其置换层的变换规律, 寻找出故障在每一轮的传播特点, 再根据其传播特点选择错误故障注入的位置, 设计出故障模型.本文所提出的两种差分故障攻击方法, 每一种攻击方法都是注入单比特的错误故障, 使S 盒的输入差分控制为1 比特.通过S 盒输出差分的值对差分分布表进行搜索, 获取S 盒输入值的一组候选值, 通过多组候选值能够筛选出S 盒的输入信息.研究结果表明, 第一种攻击方法分别在第28、27、26、25 轮S 盒运算前注入错误故障, 理论上平均192 个错误密文能够恢复全部的密钥信息; 第二种攻击方法在第一种攻击方法的基础上做出了改进, 分别在第26、25、24、23 轮S 盒运算前注入错误故障, 理论上平均32 个错误密文能够恢复全部的密钥信息.由于实验的样本空间有限, 在实验中需要错误密文数比理论值稍多, 但也能在1 秒内, 平均通过44 个错误密文恢复密钥信息.因此, 在不加防护的条件下, 本文所提出的方法能够有效地攻击GIFT 算法.

本文第2 节给出了本文所用符号的说明, 简述了GIFT 算法的密码结构和密钥编排; 第3 节介绍了差分的基本思想, 对GIFT-64-128 算法的性质进行分析; 第4 节阐述了对GIFT-64-128 算法进行差分故障攻击的攻击原理、攻击方法及攻击步骤; 第5 节给出了攻击实验的基本配置和实验结果; 第6 节总结.

2 预备知识

2.1 符号说明

具体的参数定义如下.

P: 明文;

K: 密钥;

Ki: 第i 轮的轮密钥,表示Ki的第j 个比特;

Bi: 在第i 轮, 没有注入错误的S 盒输入,表示Bi的第j 个比特;

Bi∗: 在第i 轮, 注入了错误的S 盒输入;

BiNj: 在第i 轮, 第j 个S 盒的正确输入, Bi表示BiNj的第n 个比特;

Si: 在第i 轮, 没有注入错误的S 盒输出,表示Si的第j 个比特;

Si∗: 在第i 轮, 注入了错误的S 盒输出;

SiNj: 在第i 轮, 第j 个S 盒的正确输出, SiNjn表示SiNj的第n 个比特;

C: 正确密文;

D: 错误密文.

2.2 GIFT 算法简介

GIFT 算法是一种基于SPN 结构的轻量级分组密码算法, 该算法分为两种版本, 一种是GIFT-64-128, 它的分组长度为64 比特, 密钥长度为128 比特, 轮数为28 轮; 另一种是GIFT-128-128, 它的分组长度为128 比特, 密钥长度为128 比特, 轮数为40 轮.本文是以GIFT-64-128 为例进行阐述.

2.2.1 GIFT-64-128 的轮结构

GIFT-64-128 的轮结构由非线性层、线性层以及异或密钥与轮常数组成, 如图1 所示.

(1)非线性代换: GIFT-64-128 每一轮的非线性代换都是由16 个并行的S 盒构成, 每一个S 盒都是4×4 的S 盒, S 盒代换表如表1 所示.

(2)线性置换: GIFT-64-128 的置换层改变了S 盒输出后比特位的次序, P 盒置换表如表2 所示.

(3)异或密钥与轮常数: GIFT-64-128 算法的每一轮都从128 比特的密钥集合中提取出32 比特进行运算.提取出的K 分成两个部分j ∈(0,1,··· ,15).同时,每一轮的第3、7、11、15、19、23 位都分别异或轮常数C =c0c1c2c3c4c5的一位,并且每一轮第63 位都与“1”异或.即S3=S3⊕c0,S7=S7⊕c1,S11=S11⊕c2,S15=S15⊕c3,S19=S19⊕c4, S23=S23⊕c5, S63=S63⊕1.

表1 GIFT-64-128 的S 盒代换[4]Table 1 Specifications of GIFT-64-128 S-box [4]

表2 GIFT-64-128 的P 盒置换[4]Table 2 Specifications of GIFT-64-128 bit permutation [4]

2.2.2 GIFT-64-128 算法的密钥编排与轮常数编排

密钥编排: 将128 比特的密钥放入一个4×32 的矩阵中, 即

每一轮取第一行的32 位密钥比特进入轮函数, 之后进行密钥更新.首先, 将第一行的的密钥比特分成两个组, (k0||k1||···||k15)与(k16||k17||···||k31); 然后将第一组左循环移位12 位, 将第二组左循环移位2 位;最后将矩阵每一行向上循环移动1 行.即:

轮常数编排: 首先将6 比特的轮常数置为0, (c5||c4||c3||c2||c1||c0）=(0||0||0|0||0||0), 然后左循环移动1 位, 并将c5进行异或计算, 得到新的轮常数, 即(c5||c4||c3||c2||c1||c0)→(c4||c3||c2||c1||c0||c5⊕c4⊕1).轮常数和密钥不同, 密钥是先进入轮函数再更新, 轮常数是先更新再进入轮函数.

3 GIFT-64-128 算法结构分析

3.1 GIFT-64-128 算法性质1

每4 个连续的S 盒划分成一个组, 则每一个S 盒的输入来自同一组不同的4 个S 盒的输出, 每一个S 盒的输出会去往不同组的4 个S 盒.具体传播位置置换如图2 所示.

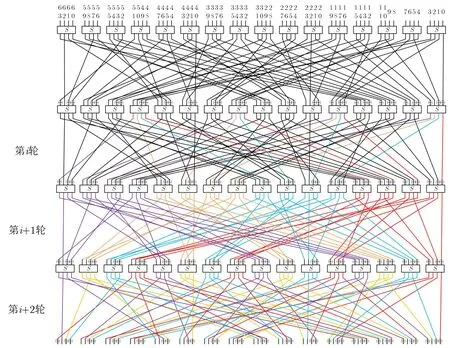
图2 GIFT-64-128 的置换图[4]Figure 2 Permutation of GIFT-64-128 [4]

3.2 GIFT-64-128 算法性质2

GIFT-64-128 算法的主密钥为128 比特, 分成4 组, 每一轮有1 组密钥参与了运算.在密钥编排中,不同组的密钥间不会互相影响, 同一组的密钥之间也只是循环移位, 因此, 得到4 轮连续的轮密钥就能求解唯一的主密钥.

3.3 GIFT-64-128 算法性质3

定义1 设IN 和IN∗是S 盒中两个不同的输入, S(IN)和S(IN∗)是它们对应的两个S 盒输出, 称∆IN′= IN⊕IN∗为S 盒的输入差分, ∆OUT′= S(IN)⊕S(IN∗)为S 盒的输出差分.每一对∆IN′都可以得到一个相应的∆OUT′, ∆IN′有24=16 种可能.对∆IN′的每一对, 可以计算出一个∆OUT′, 共可计算出16 个∆OUT′, 它们分布在24=16 个可能的值上, 这些分布的不均匀性是差分分布表的基础[19].GIFT-64-128 算法S 盒的差分性如表3 所示.

4 GIFT-64-128 算法差分故障分析

4.1 基本假设

假设满足下列攻击条件: (1)每一次攻击, 攻击者能够注入任意比特的错误; (2)每一次攻击, 攻击者能够选择在S 盒前或者在S 盒后注入错误; (3)攻击者能够选定任意的明文, 在加密过程中, 能够对后6轮注入错误, 并且能够获得相应的正确密文与错误密文.本文所提出的攻击方法的关键是通过搜索S 盒的差分分布表来寻找S 盒的输入, 进而恢复密钥.

表3 GIFT-64-128 中S 盒的差分分布表[4]Table 3 Differential distribution table of GIFT-64-128 S-box [4]

4.2 攻击方法1

4.2.1 攻击方法1 的故障模型

如图3 所示, 根据GIFT-64-128 算法非线性层的错误传播规律, 在第28 轮的S 盒运算前, 注入1 比特的错误故障, 这个错误会进入到B28Nj中, 错误比特位可能为我们假设S 盒的输入差分为∆IN′, 则∆IN′= B28Nj⊕B28∗Nj∈(0001,0010,0100,1000).通过正确密文C与错误密文D 的信息, 我们能够获得S 盒的输出差分∆OUT′.利用GIFT-64-128 算法S 盒的差分分布表, 结合输出差分∆OUT′, 可以列出一组B28Nj的候选值如表4 所示, 接着我们进一步分析整理表4,可以得到每一个S 盒的输入所对应的所有可能出现的输出差分, 如表5.通过多组候选值, 我们能够筛选出唯一的B28Nj, 进而恢复密钥信息K.

表4 GIFT-64-128 中S 盒每一个输出差分可能的输入Table 4 Possible inputs of each difference output of GIFT-64-128 S-box

4.2.2 攻击方法1 的具体步骤

(1)选择任意明文P, 在初始密钥K 下进行加密, 获取正确明文C;

(2)输入同样的明文P, 在第28 轮的S 盒运算前注入错误故障, 得到相应的错误密文D1;

(3)通过正确密文和错误密文, 找到故障的S 盒, 并求出输出差分:=P −layer−1(C ⊕D1);

图3 攻击方法1 的故障模型Figure 3 Fault model of attack algorithm 1

表5 GIFT-64-128 中S 盒输入对应的所有可能的输出差分Table 5 All possible difference output for GIFT-64-128 S-box input

(5)重复(2)–(4), 直到得到唯一的一个正确的S 盒输入;

(6)通过K28=P−layer (S−layer(B28))⊕C, 得到第28 轮的密钥K28;

(7)输入同样的明文P, 在第27 轮的S 盒运算前注入错误故障, 得到相应的错误密文D2;

(8)通过正确密文和错误密文,找到注入了故障的S 盒,并求出输出差分:=P −layer−1(S−layer−1(P −layer−1(C ⊕K28))⊕S −layer−1(P −layer−1(D2⊕K28)));

(10)重复(7)–(9), 直到得到唯一的一个正确的第27 轮S 盒输入;

(11)求解第27 轮密钥K27, K27=P −layer(S −layer(B27))⊕S −layer−1(P −layer−1(C ⊕K28));

(12)通过与上述步骤类似的方法依次恢复K26,K25;

(13)通过K25,K26,K27,K28获取唯一的一个主密钥.

4.2.3 攻击方法1 分析

在第28 轮S 盒运算前注入1 比特的故障错误, 能够得到一个S28∗Nj.根据表4 所示, 平均3 个不同的S28∗Nj能够搜索出唯一的正确B28Nj.因此, 平均48 个错误故障可以确定唯一的正确B28.最后,已知B28以及正确密文C, 可以得到密钥K28的值.

4.3 攻击方法2

4.3.1 攻击方法2 的故障模型

尽管运用攻击方法1 的故障模型能够得到GIFT-64-128 算法的全部主密钥, 但是获取每一轮的密钥都需要48 个错误故障, 恢复全部128 比特的主密钥则需要48×4=192 个错误密文.显然, 所需要的错误密文数量比较大, 在实际操作时需要占用大量的存储资源和计算资源, 因此, 我们提出了一种改进的DFA方案.

通过进一步分析GIFT-64-128 算法置换规律, 我们得出一个结论, 在第26 轮的S 盒运算前注入1 比特的故障, 能够让故障在第28 轮的扩散效果达到最大, 并且在第28 轮, 每个被影响的S 盒的输入也只有1 比特, 即∆IN′∈(0001,0010,0100,1000).接着我们再运用攻击方法1 的基本思想去求解密钥, 这样可以大量减少所需错误密文数量.攻击方法2 的攻击模型如图4 所示.

图4 攻击方法2 的故障模型Figure 4 Fault model of attack algorithm 2

4.3.2 攻击方法2 的具体步骤

本节将具体地描述用攻击方法2 攻击GIFT-64-128 算法的过程.

(1)固定明文P 和密钥K.在密钥K 的作用下, 明文P 通过加密模块后, 得到正确密文C.

(2)恢复最后一轮(第28 轮)的密钥K28, 步骤如下.

(a)在第26 轮轮函数运行之前注入1 比特的随机故障到寄存器B26Nj(0j16)中, 继续进行加密运算并得到错误密文D1.将正确密文C 与错误密文D1进行异或, 得到密文的输出差分∆D1.根据逆推轮函数的方法, 对密文的输出差分∆D1反序变换, 得到第28 轮多个S盒的输出差分∆S28Nj(0j16).∆S28Nj=P −layer−1∆D1.

(b)查找表4, 由第28 轮S 盒输出差分∆S28Nj(0j16)列出相应S 盒正确输入B28N 的候选值.

(c)在第26 轮轮函数运行之前, 多次注入1 比特的随机故障, 重复步骤(a)和步骤(b), 不断缩小S 盒正确输入B28N 的候选值的个数, 直到只剩下唯一的一个.此时得到的就是正确的S盒输入B28N.

(d)正向计算轮函数, 将正确的S 盒输入B28N 代入轮函数中, 计算得到第28 轮的密钥K28的值.K28=P −layer(S −layer(B28))⊕C.

(3)恢复倒数第二轮(第27 轮)的密钥K27, 步骤如下.

(a)确定密钥 K28的值后, 在第 25 轮轮函数运行之前注入 1 比特的随机故障到寄存器B25Nj(0j16)中, 继续加密得到错误密文D2.逆推轮函数, 将正确密文C 反序变换, 结合密钥K28, 计算出第27 轮的S27N ⊕K27.S27N ⊕K27= P −layer−1(S −layer−1(P −layer−1(C ⊕K28))); 再将错误密文D2反序变换, 结合密钥K28, 可以计算出第27 轮的S27N∗⊕K27.S27N∗⊕K27=P −layer−1(S −layer−1(P −layer−1(D2⊕K28))).进一步可以得到第27 轮S 盒输出差分∆S27N.∆S27N =S27N ⊕K27⊕S27N∗⊕K27.

(b)查找表4, 根据第27 轮S 盒输出差分∆S27Nj(0j16), 列出相应第27 轮S 盒正确输入B27N 的候选值.

(c)在第25 轮轮函数运行之前, 多次注入1 比特的随机故障, 重复步骤(a)和步骤(b), 不断缩小S 盒正确输入B27N 的候选值的个数, 直到只剩下唯一的一个.此时得到的就是正确的S盒输入B27N.

(d)正向计算轮函数, 将正确的S 盒输入B27N 代入轮函数中, 计算得到第27 轮密钥加之前的状态P −layer(S −layer(B27)), 之后通过异或B28N, 得到第27 轮的密钥值K27.K27=P −layer(S −layer(B27))⊕B28N.

(4)恢复倒数第三轮(第26 轮)的密钥K26, 步骤如下.

(a)确定密钥K27,K28的值后,在第24 轮轮函数运行之前注入1 比特的随机故障到B24Nj(0j16), 得到错误密文D3.逆推轮函数, 分别将正确密文C 和错误密文D3反序变换, 结合密钥K27、K28, 得到第26 轮S 盒输出差分∆S26N.

(b)通过与(3)相类似的方法计算出第26 轮密钥K26.

(5)恢复倒数第四轮(第25 轮)的密钥K25, 步骤如下.确定密钥K26,K27,K28的值后, 在第23 轮轮函数运行之前注入1 比特的随机故障到B23Nj(0j16), 得到错误密文D4.通过与上述(2)–(4)类似的方法恢复第25 轮的密钥K25.

(6)利用密钥编排, 逆向计算K25,K26,K27,K28, 得到唯一的一个主密钥.

4.3.3 攻击方法2 分析

根据表4 所示, 注入1 比特的故障错误, 经过S 盒后到下一轮, 有的概率保持1 比特的故障错误, 有的概率变成2 比特的故障错误, 有的概率变成3 比特的故障错误, 有的概率变成4 比特的故障错误.显而易见, 通常情况下, 在第26 轮S 盒运算前注入1 比特的故障错误, 在第28 轮能够得到至少4 个注入故障错误的B28Nj.在这种情况下, 我们恢复第28轮的密钥K28所需要的错误密文则减少到12 个.由于我们是在第26 轮的S 盒运算前注入的故障错误,因此, 在我们恢复K28的同时, 也可以得到第27 轮的24 个注入了错误的B27Nj, 只需要在第25 轮的S盒运算前, 再注入6 次错误, 得到6 个错误密文, 就可以恢复K27; 由此类推, 恢复K26需要在第24 轮的S 盒运算前, 再注入6 次错误; 恢复K25需要在第23 轮的S 盒运算前再注入8 次错误.综上所述, 理论上利用攻击方法2, 我们只需要32 个错误密文就可以获取GIFT-64-128 算法的全部主密钥.

5 攻击实验和结果对比

5.1 实验配置

本文使用一台普通PC 机进行实验, CPU 为Inter(R)Core(TM)i7-6700HQ, 主频2.60 GHz; 内存16 GB; 64 位操作系统; 使用Microsoft Visual Studio 2010 编程.

5.2 攻击实验结果

本文的故障注入是通过编程语言修改GIFT-64-128 算法的加密过程进行实现的, 再通过C++ 程序将注入随机故障所得到的错误密文进行处理, 最后记录恢复主密钥所需要的错误密文、每一轮的错误密文数量、程序运行时间及轮密钥等.我们进行了多组实验, 现仅列举其中15 组如表6 所示.表7 列举了序号1 的实验数据.

由于我们的样本空间有限, 样本的量不够多, 因此所得到的结果与理论值有所差别.我们实验中所选择的样本空间在注入故障后能有效利用的故障传播路径比理论值略少, 即每个故障注入对S 盒输入的影响比理论上略少, 要达到理论上的故障传播效果就会需要更多的错误密文, 因此, 所需要的实际错误密文数量会略多于理论值, 但平均也只需要44 个错误密文就能在1 秒内恢复全部的密钥信息.

在序号1 实验中, 我们首先固定明文为FEDCBA9876543210, 密钥为FEDCBA9876543210FEDC BA9876543210, 放入加密算法中进行加密, 获得密文C1B71F66160FF587.然后在第26 轮轮函数前, 注入故障错误, 通过注入15 次故障错误能够计算出第28 轮的轮密钥EDCF98BA;接着再依次在第25、24、23 轮轮函数前, 分别通过注入6 次、7 次、10 次的故障错误, 能够计算出第27 轮的轮密钥65471032、第26 轮的轮密钥EDCF98BA 及第25 轮的轮密钥65471032.最后, 通过逆运算密钥编排能够得出主密钥为FEDCBA9876543210FEDCBA9876543210, 与原始密钥一致, 验证了本文所提出方法的正确性, 并且通过实际分析证明, 只需较少的错误密文数量就能够恢复全部的密钥信息.

表6 差分故障攻击GIFT-64-128 算法的实验结果Table 6 Experimental result of differential fault analysis on GIFT-64-128

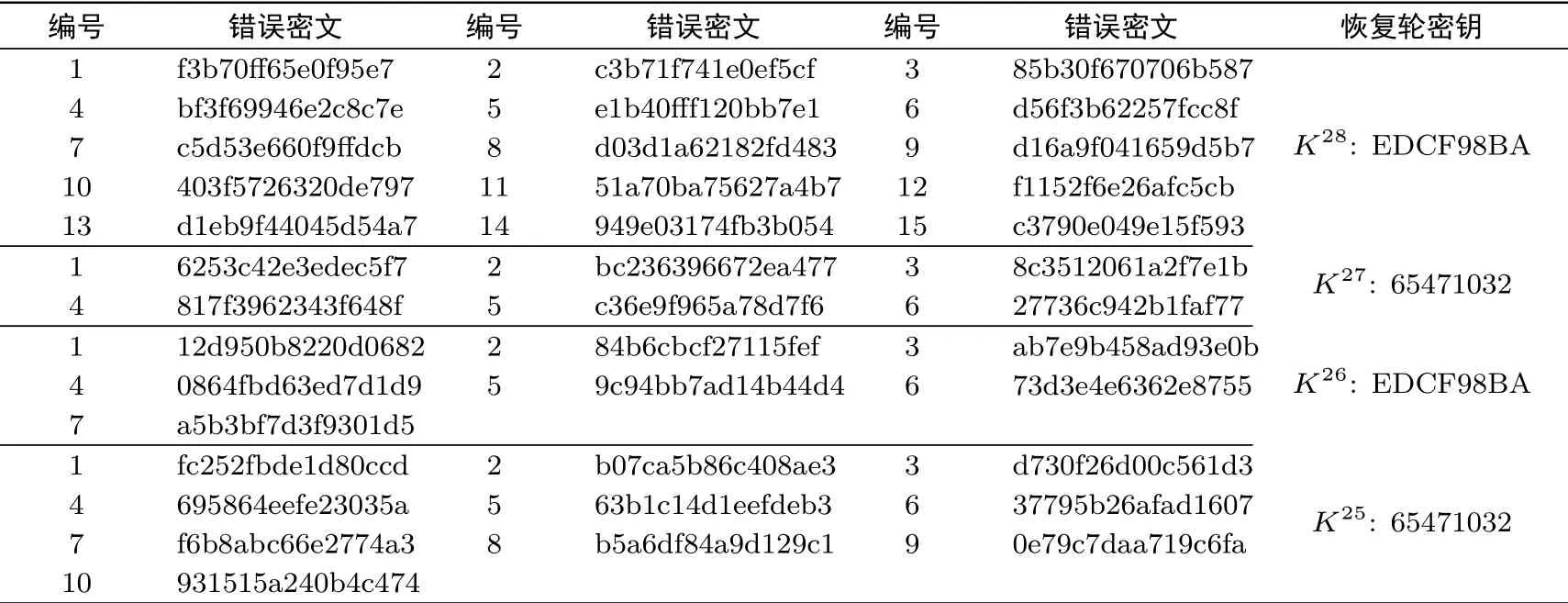
表7 差分故障攻击GIFT-64-128 算法的一组实验结果数据Table 7 One of experimental result of differential fault analysis on GIFT-64-128

本文所提出的方法还具有简单直观、通用性强的特点, 能够应用于其他轻量级密码中, 尤其是拉线类型的密码算法.尽管不同的轻量级密码有不同的置换层, 但通过研究置换层的传播规律, 找到能使错误扩散最多却又不会影响同一个S 盒的轮数, 就有可能利用本文所提出的方法恢复密钥信息.

6 总结

在选择明文攻击下, 根据GIFT-64-128 算法的置换层传播特性和S 盒的差分特性, 本文提出了两种基于单比特错误注入的差分故障攻击方法.第一种攻击方法, 理论上平均需要192 个错误密文就能够恢复全部的密钥信息.第二种攻击方法, 理论上平均需要32 个错误密文就能够恢复全部的密钥信息, 在实际验证中, 所需的错误密文数量比理论值略多, 但也仅需44 个错误密文就能在1 秒内恢复全部密钥信息.GIFT 算法应用在物联网上时如果将算法的最后7 轮额外加上一个校验轮, 并检测算法运行情况, 则能够提高抵抗故障攻击的能力.下一步, 我们将会研究注入多比特错误时, 对S 盒造成叠加影响的内在规律,进一步减少错误密文的数量; 同时我们也会尝试运用代数故障攻击等方法对GIFT 算法进行分析.

附录: 用基本DFA 方法得到B28Nj 简例

每一个字符代表的都是16 进制(例: 2 = (0010)2), x 表示任意的16 进制的数.

密文C: xxx8xxx0xxx0xxx1;

第一个错误密文D1: xxx8xxx0xxx2xxx0;

第二个错误密文D2: xxx0xxx0xxx0xxx0;

第三个错误密文D3: xxx0xxx4xxx0xxx1;