HBcipher: 一种高效的轻量级分组密码*
2019-07-16刘波涛
李 浪, 郭 影, 刘波涛, 欧 雨
1.衡阳师范学院计算机科学与技术学院, 衡阳 421002
2.智能信息处理与应用湖南省重点实验室, 衡阳 421002
1 引言
目前, 无线传感器网络与射频标签技术的应用非常广泛, 这些器件制造成本低, 且网络健壮性与自组织性强, 适用性广泛, 涉及到人们生活的各个方面.一个典型的RFID 标签具有1000–10 000 个标准门电路, 但是用于保障信息安全分组密码算法仅能占用200–2000 个门电路.一般采用两种方案来降低面积资源: 一种是对传统分组密码进行不断地优化和提高硬件工艺, 其中已有不少学者对AES 密码不断地优化实现[1–4]; 另一种是设计低资源面积、高效的轻量级分组密码.轻量级分组密码最近几年引起密码学者的高度重视.
香农提出的扩散和混淆概念奠定了密码算法的基本安全性[5].一个分组密码算法的扩散层通常是通过一个线性扩散矩阵实现, 通过线性运算将输入向量转换成输出向量[6].但是在有限的计算资源下, 找到安全性与执行效率的最佳平衡点是困难的.混淆则是尽量使密文与密钥之间的统计关系复杂化, 使用复杂的非线性变换可以达到比较好的混淆效果.目前已提出了一些轻量级分组密码, 例如DESL/DESX/DESXL[7]、Hummingbird[8]、Magpie[9]、QTL[10]、LBlock[5]、KLEIN[11]、LED[12]、PRESENT[13]、TWINE[14]等.PRESENT 在CHES 2007 上提出, 由于其简洁的密码结构、良好的硬件性能和安全性, 引起了广泛关注.PRESENT 硬件实现高效, 因为其扩散层采用基于比特的排列置换, 这在硬件中只需要连线实现.2012年, PRESENT 被采纳为ISO/IEC 轻量级密码标准.许多轻量级分组密码, 例如PRESENT、KATAN/KTANTAN[15]和Hummingbird, 在硬件方面的实现效率都很高, 但软件实现性能不佳.正如文献[13,16–18]中指出的密码算法也需要很高的软件实现性能, 与面向硬件的设计相比, 软件实现具有更好的灵活性和更低的成本.
本文结构如下安排.第2 节对HBcipher 密码算法进行设计与实现, 第3 节从各个层次介绍HBcipher算法的设计原理, 第4 节用多种分析方法对算法进行安全性评估, 第5 节描述算法的硬件实现所占资源以及各算法所占资源对比, 第6 节描述算法软件实现性能以及对比, 第7 节是总结.
2 HBcipher 算法设计与实现
在本节中, 我们详细叙述HBcipher 的结构和各个组件的设计方法与实现.
2.1 符号定义

2.2 加密算法HBcipher
HBcipher 分组长度为64 位, 密钥长度设计为64 位和128 位两种.当密钥长度为64 位时, 迭代轮数为32, 记为HBcipher-64; 当密钥长度为128 位时, 迭代轮数为40, 记为HBcipher-128; 轮函数采用三组SPN 结构的F 函数, 如图1 所示.令P =L ∥R 表示64 位明文.

图1 HBcipher 加密结构图Figure 1 Encryption structure of HBcipher
动态轮密钥加:HBcipher 算法选取轮数作为轮运算控制信号, 输入64 位明文P 与64 位密钥K(或输入128 位密钥K, 但每一轮仅选取轮密钥前64 位参与动态轮密钥加运算), 64 位密钥K 以4×16 的矩阵形式表示, 矩阵左边8 列记为
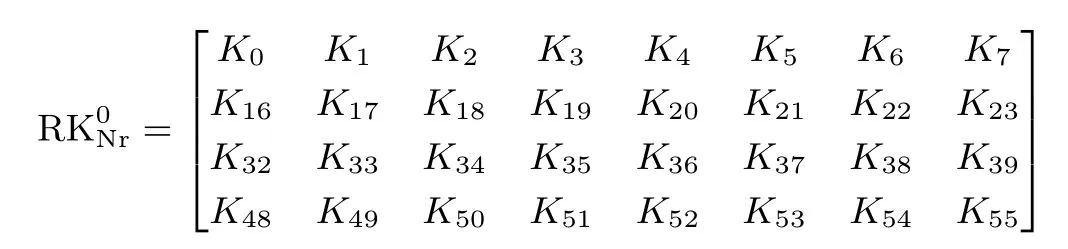
右边8 列记为
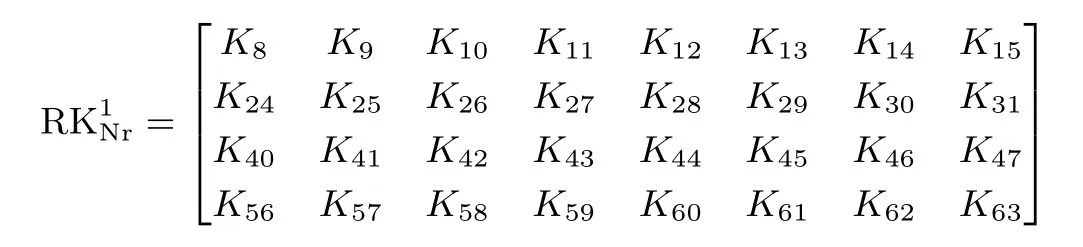
(Nr 表示轮数), 即所述:
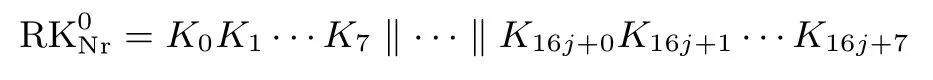

其中, j =0,1,2,3, Nr=1,2,··· ,32.当轮运算控制信号count 为奇数时:
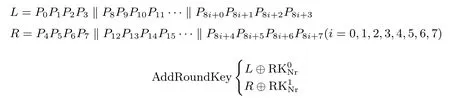
当轮运算控制信号count 为偶数时:
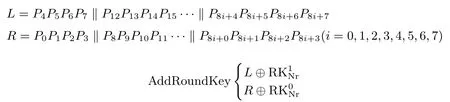
轮函数:HBcipher 算法轮函数采用三组SPN 结构的F 函数, 分别为F1、F2、F3.F1包括轮密钥加、S 盒替换和行移位, 如图2 数据流程图所示; F2包含轮密钥加、S 盒替换和轮常数加, 如图3 数据流程图所示; F3仅包括P2置换, 如图4 数据流程图所示.

图2 F1 函数流程图Figure 2 Flowchart of F1 function
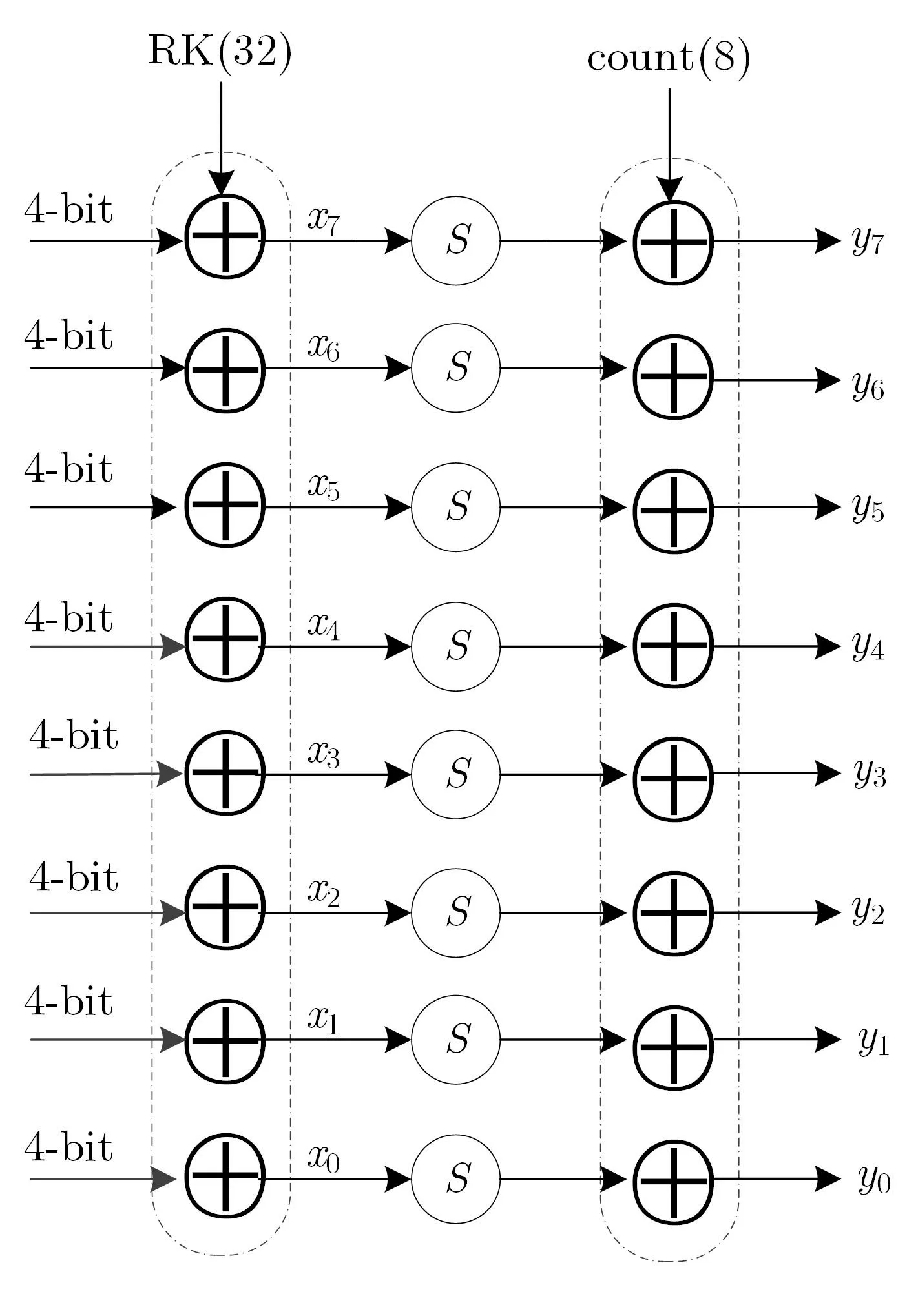
图3 F2 函数流程图Figure 3 Flowchart of F2 function

图4 F3 函数流程图Figure 4 Flowchart of F3 function
S 盒置换:在HBcipher 算法非线性层设计中, 引用PRESENT 算法加密的S 盒, 主要用于函数变换和密钥更新模块中, S 盒元素如表1 所示.

表1 S 盒元素值Table 1 Value of S-box
行移位变换:对于4×8 的矩阵, 矩阵每一行左循环不同的比特, 第一行循环左移3 个比特, 第二行循环左移5 个比特, 第三行循环左移6 个比特, 第四行循环左移7 个比特, 如图5 所示.

图5 行移位操作示意图Figure 5 Diagram of ShiftRow
常数加:在加密第1、5、9、13、17、21、25、29 (33、37)轮时, 轮常数count 与数据高8 位进行常数加运算; 在加密第2、6、10、14、18、22、26、30 (34、38)轮时, 轮常数count 与数据高9–16 位进行常数加运算; 在加密第3、7、11、15、19、23、27、31 (35、39)轮时, 轮常数count 与数据低9–16位进行常数加运算; 在加密第4、8、12、16、20、24、28、32 (36、40)轮时, 轮常数count 与数据低8位进行常数加运算, 常数加变换操作如图6.

图6 常数加变换操作Figure 6 Diagram of AddConstants
P2 置换:经过F1、F2变换的4×16 状态矩阵如图7 所示.

图7 P2 置换示意图Figure 7 Diagram of P2
区域①对称映射到区域②, 原区域②则以直角顶点顺时针旋转90 度对称映射到区域③, 以此类推, 原区域⑧以直角顶点逆时针旋转90 度对称映射到原区域①, 而区域A 对称映射到区域D, 区域B 则对称映射到区域A, 同理, 区域C 对称映射到区域B, 区域D 对称映射到区域C, 经过上述操作后所形成的P2置换元素表格如图8 所示.
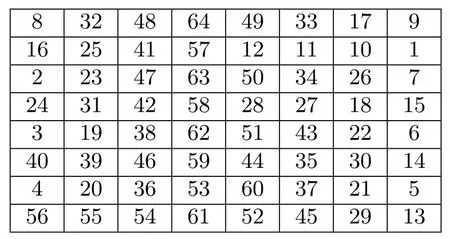
图8 P2 置换表Figure 8 Permutation table of P2
白化密钥加:为避免最后一轮完全暴露给攻击者, 对各种攻击提供方便, 我们在最后一轮P2置换输出后, 增加白化密钥加.HBcipher-128 算法中选取前64 位初始密钥进行白化密钥加运算.
2.3 密钥更新
HBcipher 有64 和128 位的两种密钥更新模式.
64 位密钥:将用户提供的64-bit 密钥K =k0k1···k62k63存储在64-bit 密钥寄存器中:

密钥寄存器更新方式如下:
(1)第0 列和第15 列进行S 盒置换.

(2)64 位的密钥经过P1置换后第i 列移动到P1(i)列, P1置换表元素如表2, 如下式(1)所示:
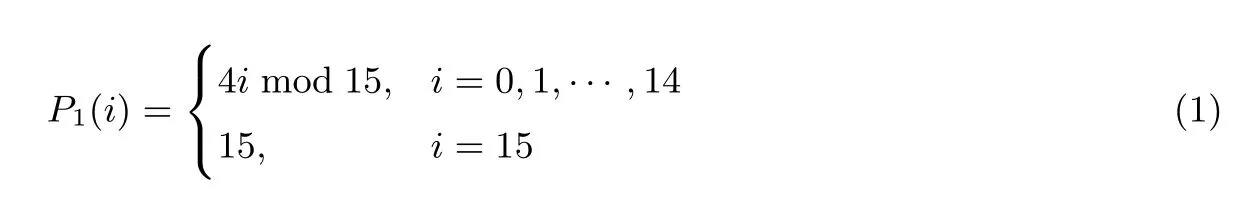

表2 HBcipher-64 P1 置换表Table 2 Permutation table of P1
(3)每行都循环左移不同的单位, 第一行循环左移7 位, 第二行循环左移9 位, 第三行循环左移11 位,第四行循环左移13 位.
128 位密钥:将用户提供的128-bit 密钥K =k0k1···k126k127存储在128-bit 密钥寄存器中.

在加密第count(count=1,2,··· ,40)轮时, 选取前四行作为轮密钥, 密钥寄存器更新方式如下:
(1)第0 列和第15 列进行S 盒置换.
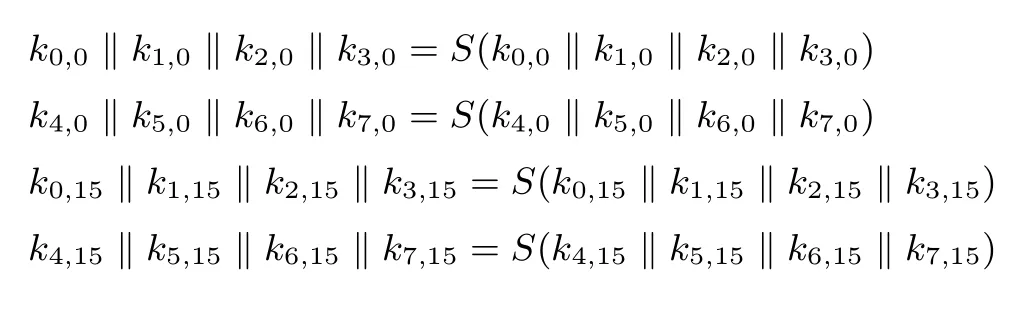
(2)每一行都循环左移不同的单位且循环上移1 行, 具体移位方式如图9 所示.
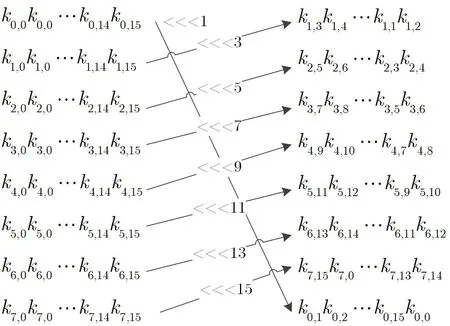
图9 移位示意图Figure 9 Diagram of shift
2.4 HBcipher 解密算法
HBcipher 算法是基于SPN 结构的轻量级密码算法, 其解密过程与加密过程相反, 通过把输入密文和密钥由轮函数经Nr 轮迭代来实现, 解密轮密钥是加密轮密钥的逆序使用.其解密过程具体由白化密钥运算、P2逆置换、行移位逆变换、轮常数加逆变换、S 盒逆变换、轮密钥加逆变换组成.以下将具体介绍各模块.
白化密钥运算:待解密数据与初始密钥异或操作.
P2 逆置换:P2逆置换过程与HBcipher 算法加密过程相反, 逆置换表如图10 所示.
行移位逆变换:解密过程的行移位逆变换与加密过程相反, 操作示意图如图11 所示.
轮常数加逆变换:解密过程的轮常数加变换与加密过程相反, 轮常数逆序使用.
S 盒逆变换:解密S 盒元素如表3 所示.

图10 P2 置换表Figure 10 Permutation table of P2
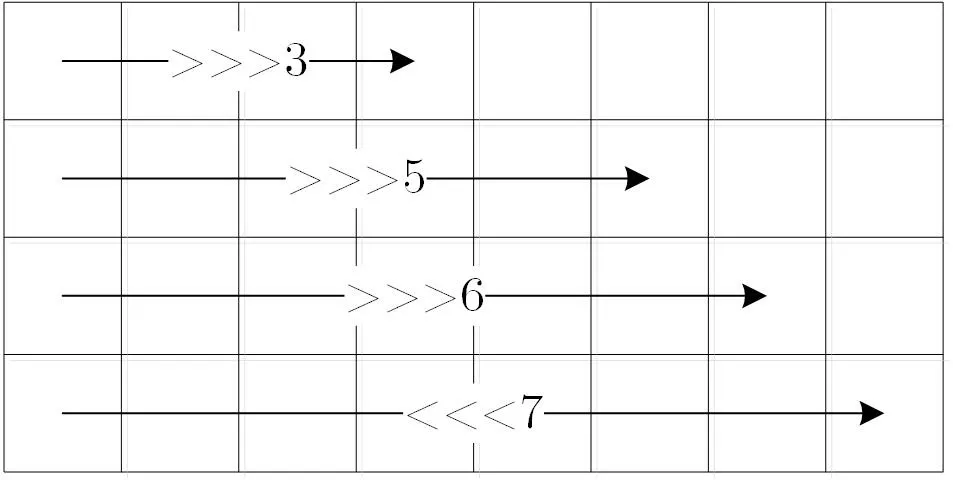
图11 行移位逆变换Figure 11 Diagram of inverse ShiftRow

表3 解密算法逆S 盒Table 3 Value of inverse S-box
3 HBcipher 设计原理
3.1 算法结构
HBcipher 是基于SPN 结构的轻量级分组密码算法, 轮函数采用3 组微型SPN 结构函数, 分别为F1、F2和F3.64 位的初始明文P 根据轮运算控制信号count 的奇偶性动态划分成两个32 位的数据块并行执行F1、F2函数后, 恢复64 位执行F3, 得出密文.该种结构模式下, 待加密数据根据算法轮运算控制信号奇偶性动态选择更新后的子密钥, 且每轮待加密数据划分原则的不同相当于一次基于比特的位置换, 在保证了加密速度的前提下充分隐藏明文的统计特性, 提高算法抗统计分析能力.
3.2 动态轮密钥加结构
在动态轮密钥加操作中, 首先, 需要将轮子密钥进行划分两部分与同时还对待加密数据进行划分两部分L 与R.在轮子密钥与待加密密钥的划分过程实现操作, 相当于对子密钥与待加密数据进行了移位操作.然后, 当轮运算控制信号count 为奇数时, 轮密钥加操作为与当轮运算控制信号count 为偶数时, 轮密钥加操作为与这种根据轮运算控制信号进行动态选择的轮密钥加与一般静态的算法的轮密钥加的操作相比, 更具有灵活性与安全性, 特别是抵抗自相似攻击, 而动态轮密钥加对于HBcipher 算法整体安全性影响, 本文第4 节对算法的安全性分析已证明.
3.3 非线性层
密码设计时不仅要硬件和软件实现性能之间的平衡, 也要考虑硬件实现和算法安全性能之间的关系.虽然采用大S 盒可以实现更好的安全性, 但即使在软件中, 大S 盒也需要高昂的存储成本, 而且硬件实现要差得多; 另一方面, 太小的S 盒难以达到合适的安全性.我们观察到门数随S 盒的大小呈指数增长, 所以选取了目前最具有代表性的轻量级分组密码PRESENT 的4×4 小S 盒, 做到硬件效率、软件实现以及安全性能三者之间的折中.
3.4 线性层
在HBcipher 算法加密流程、密钥更新以及轮函数的设计中使用了大量置换、移位等操作.在动态轮密钥加操作中, 根据轮运算控制信号的奇偶性动态选择子密钥与待加密数据进行异或, F1函数中的行移位操作, F2函数中的常数加操作以及F3函数中的P2置换.为避免最后一轮完全暴露给攻击者, 对各种攻击提供方便, 我们在最后一轮P2置换输出后, 增加白化密钥加运算.使用这些变换和运算的目的主要有两方面: 一是方便软硬件实现; 二是提高HBcipher 算法的抗攻击强度, 这些变换在一定程度上具有快速扩散的作用, 隐藏了明文和密钥信息、从而使明文与密钥之间不具有统计特性.
4 安全性分析
4.1 雪崩效应
在密码学中, 雪崩效应是指任意一组明文输入, 随机改变其中一个输入位, 将导致至少有一半以上的输出位发生改变.若某种分组密码没有显示出一定程度的雪崩特性, 那么它可以被认为具有较差的随机化特性, 而且密码攻击者可以利用输出数据推测输入数据, 因此, 从加密算法的设计角度来说, 满足雪崩效应是充要条件, 为了测试HBcipher 算法是否满足雪崩效应, 我们用两个实验进行验证.
在实验1 中, 固定一条64 位明文, 随机选择一条64 位初始密钥进行加密得到初始密文, 将初始密钥中各位按位取反, 得到64 条密钥, 分别将64 条密钥与固定明文进行加密得到64 条密文, 将64 条密文分别与初始密文进行异或操作, 统计每条异或结果中出现1 的次数, 1 的次数代表了当改变其中一个输入位时, 有多少输出位发生改变, 实验结果如图12, 图12 中1 的平均数值是32.3125, 大于明文输入位数值的一半.

图12 改变密钥的雪崩效应统计图Figure 12 Statistical map of avalanche effect with changed key
在实验2 中, 固定一条64 位密钥, 随机选择一条64 位初始明文进行加密得到初始密文, 将初始明文中各位按位取反, 得到64 条明文, 分别将64 条明文与固定密钥进行加密得到64 条密文, 将64 条密文分别与初始密文进行异或操作, 统计每条异或结果中出现1 的次数, 1 的次数代表了当改变其中一个输入位时, 有多少输出位发生改变, 实验结果如图13, 图13 中1 的平均数值是32.296 88, 大于明文输入位数值的一半.

图13 改变明文的雪崩效应统计图Figure 13 Statistical map of avalanche effect with changed plaintext
由图12 和图13 的统计结果可知, HBcipher 算法具有良好的雪崩性.
4.2 HBcipher 算法的差分密码分析
差分密码分析方法是攻击迭代型分组密码最有效的方法之一, 也是衡量一个分组密码安全性的重要指标之一.差分密码分析的本质就是研究差分在加密(解密)过程中的概率传播特性.本小节主要介绍对HBcipher 算法加密差分密码分析过程.
定义1迭代分组密码的一条i 轮差分特征Ω = (β0,β1,··· ,βi−1,βi), 是指当输入对(X,X∗)的差分值满足X ⊕X∗= β0, 在i 轮加密过程中, 中间状态(Yj,的差分值满足Yj⊕= βj, 其中1ji.当i=1 时, 差分(α,β)和差分特征(β0,β1)概念统一, 表征轮函数的差分传播特性.
定义2迭代分组密码的一条i 轮差分(α,β)所对应的概率DP(α,β), 是指在输入X、轮密钥K1,K2,··· ,Ki取值独立且均匀的情况下, 当输入对(X,X∗)的差分值X ⊕X∗= α, 经过i 轮加密后,输出对(Yi,的差分值满足Yi⊕Y∗i= β 的概率, 当i = 1 时, DP(α,β)表示轮函数的的差分传播概率.
定义3迭代分组密码的i 轮差分特征Ω = (β0,β1,··· ,βi−1,βi)所对应的概率DP(Ω)是指在输入X、轮密钥K1,K2,··· ,Ki取值独立且均匀的情况下, 当输入对(X,X∗)的差分值X ⊕X∗=α, 经过i轮加密后, 中间状态(Yj,的差分值满足Yj⊕= βj的概率, 其中0ji.在上述假设下, 差分特征概率等于各轮差分传播路径的乘积.
定义4给定两条差分特征Ω1= (β0,β1,··· ,βs), Ω2= (γ0,γ1,··· ,γt), 若βs= γ0, 则称Ω =(β0,β1,··· ,βs,γ1,··· ,γt)为Ω1和Ω2的级联, 此时DP(Ω)=DP(Ω1)×DP(Ω2).
定义5若一条i 轮差分特征Ω = (β0,β1,··· ,βi−1,βi)满足β0= βi, 则称Ω 是一条i 轮迭代差分特征, 若Ω 是迭代差分特征, 则自身可进行级联.
定义6设m,n ∈Ν , 从到的非线性映射记为: S:给定α ∈定义INS(α,β)=x ∈:S(x ⊕α)⊕S(x)=β,NS(α,β)=#INS(α,β).
定义7考虑轮函数F 的一对输入(X,X∗), 若该输入对导致某个S 盒的输入差分非0, 则称输入对导致该S 盒活跃, 简称该S 盒为差分活跃S 盒.
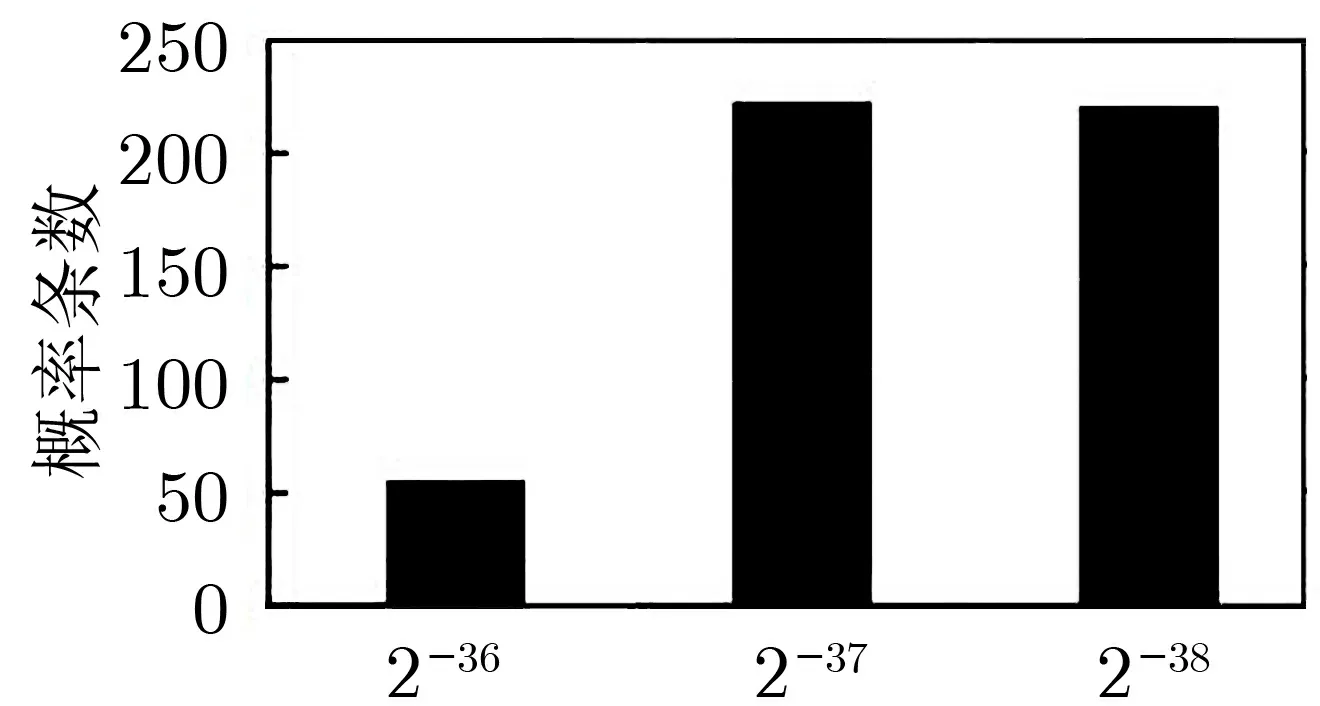
图14 500 条HBcipher 算法4 轮差分特征概率统计图Figure 14 Probability statistics of 500 4-rounds differential characteristics of HBcipher algorithm
根据定义1 寻找差分特征, 给定输入差分, 跟踪轮函数迭代过程, 到达某个输出差分, 这一过程即对应一条差分特征.本文假定输入差分值, 依据附录B 表9 HBcipher 算法S 盒的差分分布表得到S 盒的输出差分, 跟踪HBcipher 算法轮函数的迭代过程, 到达第4 轮S 盒的输出差分, 随机截取500 条HBcipher 算法的4 轮差分特征, 得到3 条差分特征概率值, 如图14 柱形图所示, 其中56 条差分特征的概率值为2−36, 223 条差分特征的概率值为2−37, 221 条差分特征的概率值为2−38.当使用差分攻击手段攻击n-bit 分组密码时, 在整个加密过程中必定只有极少轮数差分特征能大于21−n, 对于HBcipher 算法, 根据定义5 和6, 假设HBcipher 算法差分特征为迭代差分特征, 那么500 条HBcipher 算法32 轮差分特征上限为2(−36)×8= 2−288.这个差分概率非常小, 因此32 轮的HBcipher 算法具有足够抵抗差分攻击的能力.
4.3 HBcipher 算法的线性分析
定义8设X ∈{0,1}n, X 的线性掩码定义为某个向量ΓX ∈{0,1}n, ΓX 和X 的内积ΓX ·X 代表X 某些分量的线性组合.即
定义9迭代分组密码的一条i 轮线性特征Ω = (β0,β1,··· ,βi)是指当输入掩码为β0, 在i 轮加密过程中, 中间状态Yj的掩码为βj, 其中1ji.
定义10迭代分组密码的一条i 轮线性特征Ω = (β0,β1,··· ,βi)所对应的线性概率LP(Ω)是指在输入X、轮密钥K1,K2,··· ,Ki取值独立且均匀的情况下, 当输入掩码为β0, 在加密过程中, 中间状态Yj的掩码取值为βj的线性概率, 其中1ji.
定义11给定两条线性特征Ω1= (β0,β1,··· ,βs), Ω2= (γ0,γ1,··· ,γt), 若βs= γ0, 则称Ω =(β0,β1,··· ,βs,γ0,γ1,··· ,γt)为Ω1和Ω2的级联, 此时LP(Ω)=LP(Ω1)×LP(Ω2).
定义12若一条i 轮线性特征Ω=(β0,β1,··· ,βi−1,βi)满足β0=βi, 则称Ω 是一条i 轮迭代线性特征, 若Ω 是迭代线性特征, 则自身可进行级联.
定义13设m,n ∈Ν, 从到的非线性映射记为: S:给定α ∈定义INS(α,β)= x ∈α·x=β·S(x),NS(α,β)= #INS(α,β).构造2m×2n的表格: 以α (S 盒的输入掩码)为行指标遍历β(S 盒的输出掩码)为列指标遍历行列交错项取值为NS(α,β)−2m−1.以上述方式构造的表称为线性逼近表.
HBcipher 算法S 盒线性逼近表如附录B 表10 所示.
定义14在一条i 轮线性特征中Ω = (β0,β1,··· ,βi)中, 若第j 轮(ji)输出掩码βj, 导致某个S 盒的输出掩码非0, 则称这条线性特征导致该S 盒活跃, 简称该S 盒是线性活跃S 盒.
根据定义寻找一条线性特征, 给定输入掩码, 跟踪轮函数迭代过程, 到达某个输出掩码, 这一过程即对应一条线性特征.本文假定S 盒输入掩码值, 根据附录B 表10, S 盒线性逼近表得到输出掩码值, 跟踪HBcipher 算法轮函数迭代过程到第4 轮S 盒输出掩码结束, 随机截取500 条HBcipher 算法的4 轮线性特征, 得到2 条线性特征概率.如图15 柱形图所示, 其中224 条线性特征的概率值为−2−22, 276 条线性特征的概率值为2−22.根据定义11 与定义12, 假设HBcipher 算法线性特征具有迭代性, 那么HBcipher算法500 条32 轮线性特征概率上限为2(−22)×8= 2−196, 这个差分概率非常小, 因此32 轮的HBcipher算法具有足够抵抗线性分析的能力.
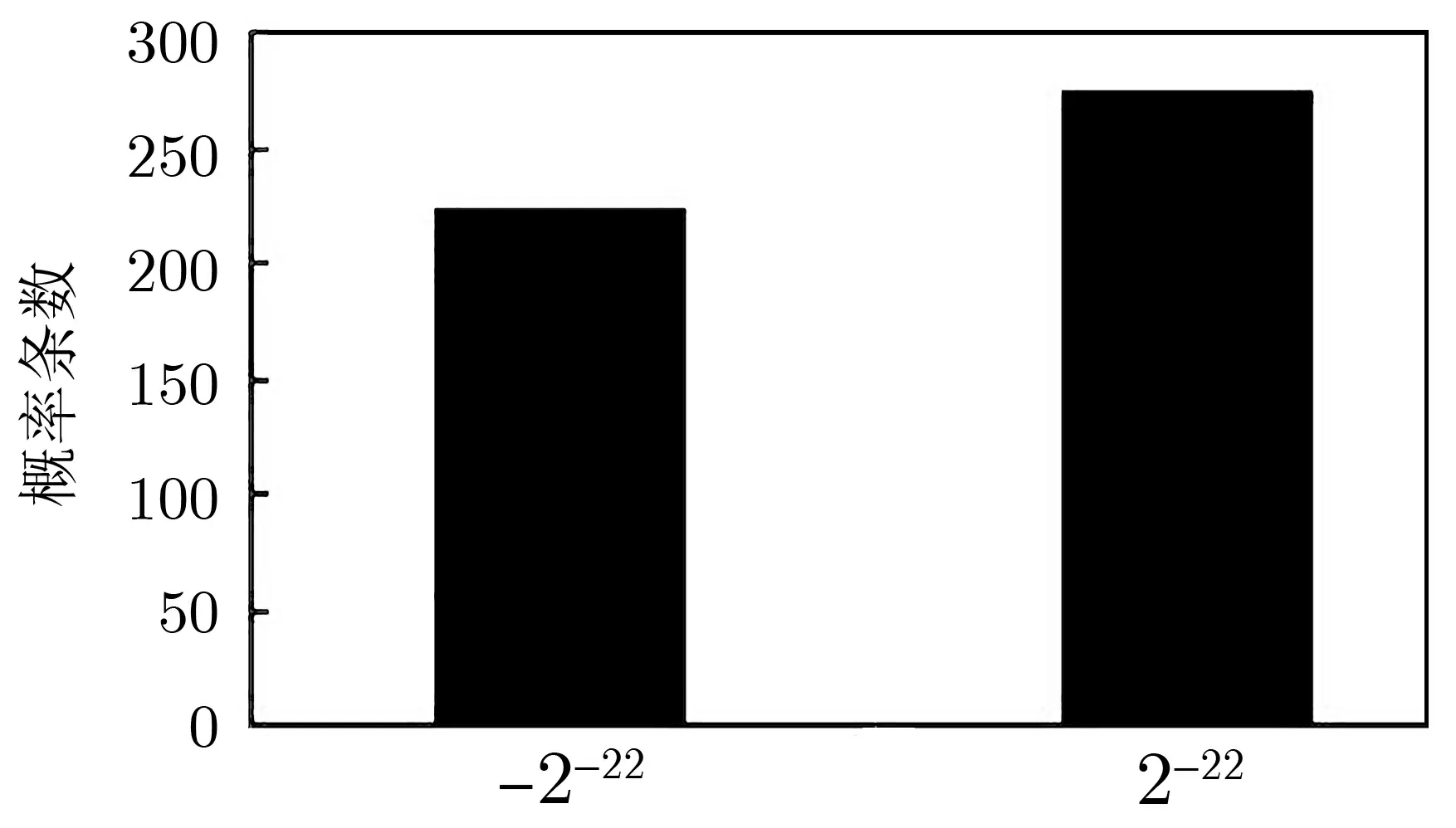
图15 500 条HBcipher 算法4 轮线性特征概率统计图Figure 15 Probability statistics of 500 4-rounds linear characteristics of HBcipher algorithm
4.4 代数攻击
代数攻击是把对密码系统的攻击问题转化为求解与之相对应的代数方程组, 由Courtois 和Pieprzyk在分析AES 时提出的[19].任意4-bit S 盒至少可以用21 个二次方程来表示, 所以整个密码在n×8 个变量中有n×21 个二次方程(n 是整个加密算法和密钥扩展中S 盒数量).在HBcipher-64 算法中我们有n = 32×16+64 = 576 个4-bit S 盒, 即在4608 个变量中有12 096 个方程.HBcipher-128 算法中有n=40×16+160=800 个S 盒, 即在6400 个变量中有16 800 个方程.文献[19]采用工作因子来估计分组密码上XSL 攻击复杂度, 对于HBcipher-64, 本文据此估计如下:
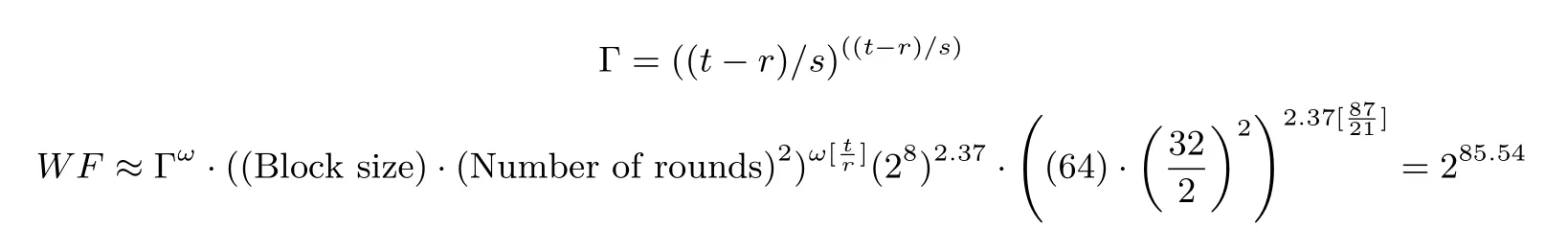
这超出了穷举搜索所需的264个操作, 从而HBcipher 算法是能够抵抗代数攻击.
4.5 相关密钥攻击
相关密钥攻击是一种利用密钥调度的弱点来进行分析的攻击方法.在相关密钥攻击模型下, 攻击者能够通过某种方式获得明文及其在某些未知密钥下对应的密文, 攻击者虽然并不知道这些密钥的具体取值,但可以了解或者选取这些密钥之间的关系.密钥扩展不同于轮函数中行移位的旋转变换, 同时采用依据轮数控制迭代次数的方式, 由文献[20]相关安全性证明可知HBcipher 的密码特性能够抵抗相关密钥攻击.
5 硬件实现
HBcipher 算法能高效地在硬件中实现, 我们通过实验计算了硬件实现所需要花费的资源.在Ubuntu 14.04 平台上进行了仿真, 在Synopsys Design Compiler Version B-2008.09 进行综合, 其中综合工艺库为SMIC 0.18m CMOS, 在综合实验结果当中, 用等效门数GE 来衡量面积资源, 1 GE 相当于一个双向与非门.有限状态机用于生成控制逻辑, 明文和密钥通过多路复用器加载到每个寄存器中.然后在接下来的时钟周期中, 数据从寄存器中读出, 通过状态和关键数据路径并分别存回寄存器, 最后可以在64 位输出中获得密文.HBcipher-64 算法数据通路图如图16 所示, HBcipher-128 数据通路图类似于HBcipher-64.
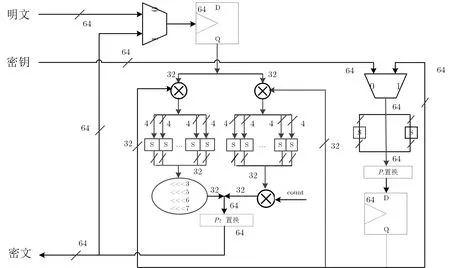
图16 HBcipher-64 数据通路图Figure 16 Data path diagram of HBcipher-64
加密算法HBcipher-64 存储64 位明文需要384 GE, 密钥异或需要174 GE, 且F2 中有一个8位的常数加运算, 由于算法选取轮数作为轮常数不需要花费寄存器, 所以该运算需要资源为27 GE.HBcipher-64 算法一个S 盒的实现资源需要24 GE, P 置换、以及行移位的硬件实现是通过连线操作, 从而不需要花费硬件资源.此外, 其它资源需要15.25 GE.HBcipher-128 存储64 位明文需要384 GE, F1与F2中的两个32 位密钥加需要174 GE, 且F2中有一个8 位的常数加运算需要资源为27 GE, S 盒需要480 GE, 存储128 位的密钥需要576 GE, 此外, 其它资源需要15.25 GE.表4 列出了HBcipher-64 和HBcipher-128 的各层次加密所需资源及占比大小.HBcipher 算法解密逆运算跟加密运算硬件资源实现时, 具有相同的资源.
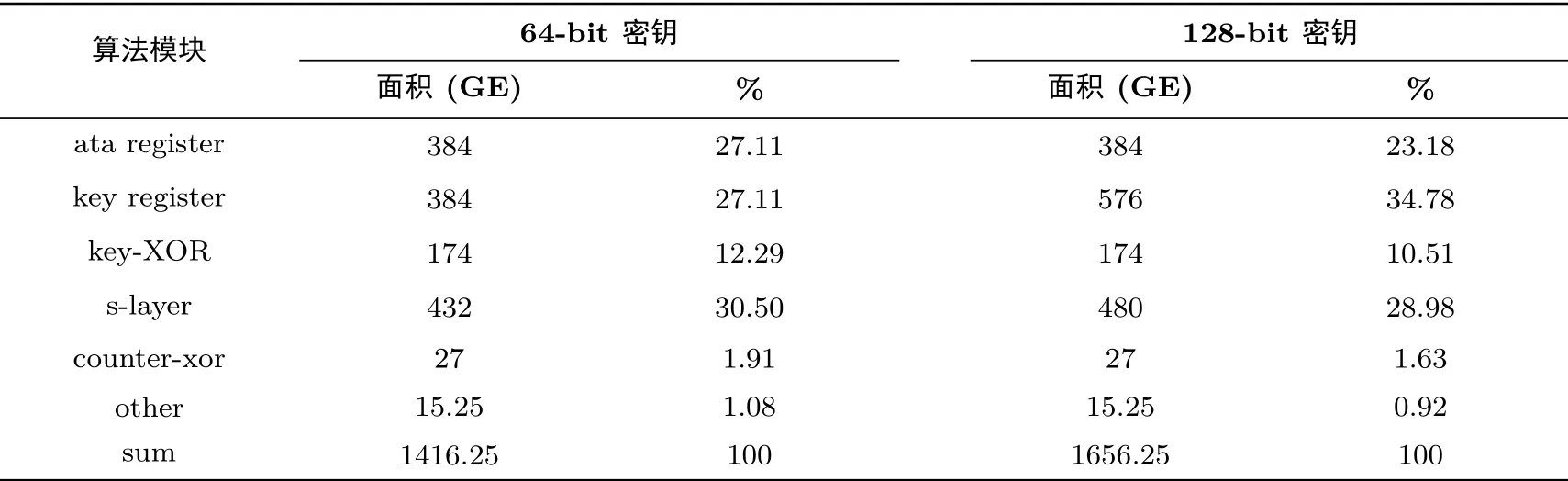
表4 HBcipher-64 和HBcipher-128 的各模块所需资源及占比大小Table 4 Resource and scale of modules for HBcipher-64 and HBcipher-128
表5 列出了各算法硬件实现面积对比, 通过对比我们可以看到HBcipher 算法加密所需的实现面积与偏向软件实现的RECTANGLE 算法相比, 其占用面积资源较小, 适合于资源受限的环境, HBcipher 算法解密性能与加密保持一致.

表5 各算法硬件实现面积对比Table 5 Area comparison of hardware implementation
6 软件实现
目前大多数轻量级密码算法都是面向硬件实现而设计的, 对于轻量级密码算法实现性能的研究也多集中在硬件实现上, 对软件实现的研究相对较少.然而, 事实上, 如果应用环境中的目标平台能够支持密码算法采用软件实现, 那么不仅比硬件实现节约成本, 而且实现及维护起来也方便.
本文将讨论在X86 体系架构上的采用位片实现HBcipher 算法的性能.HBcipher 算法加密成本的一个重要部分是S 盒, 但是位片法允许在几个时钟周期内并行计算S 盒中的大部分内容.本文中S 盒采用文献[18]中提供的逻辑指令序列实现, 假设输入为: r3,r2,r1,r0,t, 输出为: r3,r2,r1,r0, 则HBcipher的S 盒可由下列逻辑指令序列实现:
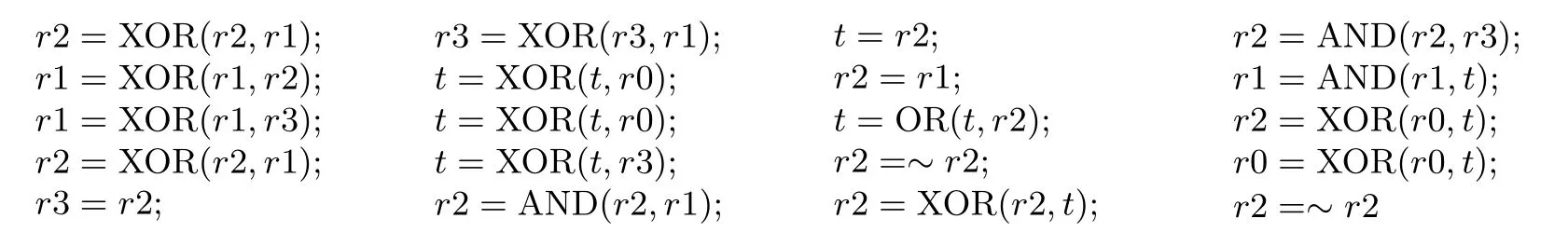
线性扩散层是HBcipher 算法加密成本的另一个重要部分, 行移位只需执行几个pshufb 操作, P2置换层可以通过以比特形式重组xmm 寄存器的16 位(或32 位)字的位置来执行, 轮常数加以事先存储的常量完成, 而列混淆可以采用与AES 中相同的方法.
对于服务器与设备D 之间的通信, 服务器必须对64 位数据块B 进行加密.假设执行加密过程所需的时间为tE(包括密钥更新, 但是没有输入/输出数据的打包/解包).在加密过程中一次加密块的数量为PE, 同样, 假设实现执行密钥更新过程(不包含密钥数据)所需的时间为tKS, 则执行一次密钥更新过程所需的块数量为PKS.假设加密比PE或PKS更少的数据块仍然需要时间tE或tKS.但是, 与加密过程或密钥更新过程相反, 输入/输出数据的打包/解包时间将很大程度上取决于所涉及块的数量.因此, 如果我们用tpack表示打包一个数据块所需的时间, 那么打包x 块只需要x·tpack.同样, 我们用tunpack表示解包一个数据块所需的时间, 解包x 个块只需要x·tunpack.对于密钥更新, tpackKS表示打包密钥数据的时间, 并且打包x 个密钥需要x·tpackKS.最后, 根据D 和B, 使用并行操作模式加密所有D·B 数据块所需的每块平均时间由下式给出[16]:

PRESENT 是典型的面向硬件实现的轻量级分组密码算法, 通过表6 各个算法软件实现性能的比较,得到HBcipher 算法加密的软件性能优于PRESENT 算法, 且接近RECTANGLE 算法.HBcipher 算法解密实现性能与加密保持一致.
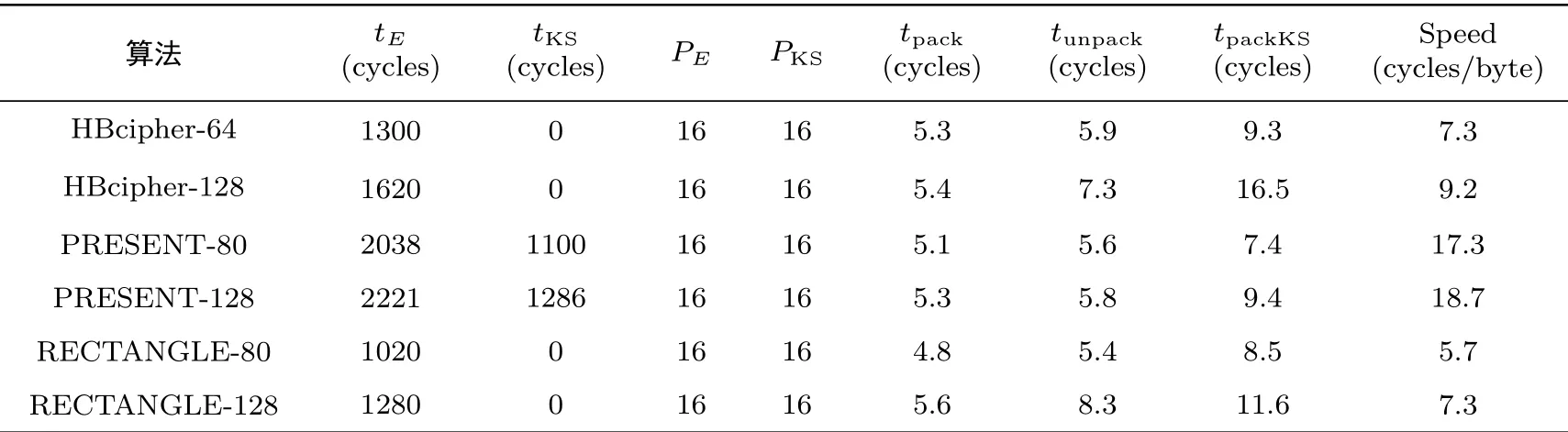
表6 软件实现性能表Table 6 Software implementation performance table
7 结论
本文中我们介绍了HBcipher 算法.我们的设计目标是做到算法在硬件效率、软件实现以及安全性能三者之间的折中.首先, 在动态轮密钥加操作中, 根据轮运算控制信号的奇偶性动态选择子密钥与待加密数据进行异或, 这种根据轮运算控制信号进行动态选择的轮密钥加与一般静态的算法的轮密钥加的操作相比, 更具有灵活性与安全性, 特别是抵抗自相似攻击.然后, 算法采用4 位非线性S 盒以减少能耗, 通过实验, 验证了HBcipher 算法满足雪崩效应的充要条件, 与偏向硬件实现的PRESENT 算法相比其软件实现性能更优越, 而与偏向软件实现的RECTANGLE 算法相比其硬件实现面积更小.最后, 通过安全性分析, 证明算法具有抵抗差分攻击与线性攻击等已知攻击的能力.
附录A 测试向量
分别给出了HBcipher-64、HBcipher-128 的测试向量如表7 和表8, 表中数据用十六进制表示.

表7 HBcipher-64 测试数据Table 7 HBcipher-64 test data

表8 HBcipher-128 测试数据Table 8 HBcipher-128 test data
附录B

表9 HBcipher 算法S 盒差分分布表Table 9 Differential distribution of S-box of HBcipher algorithm
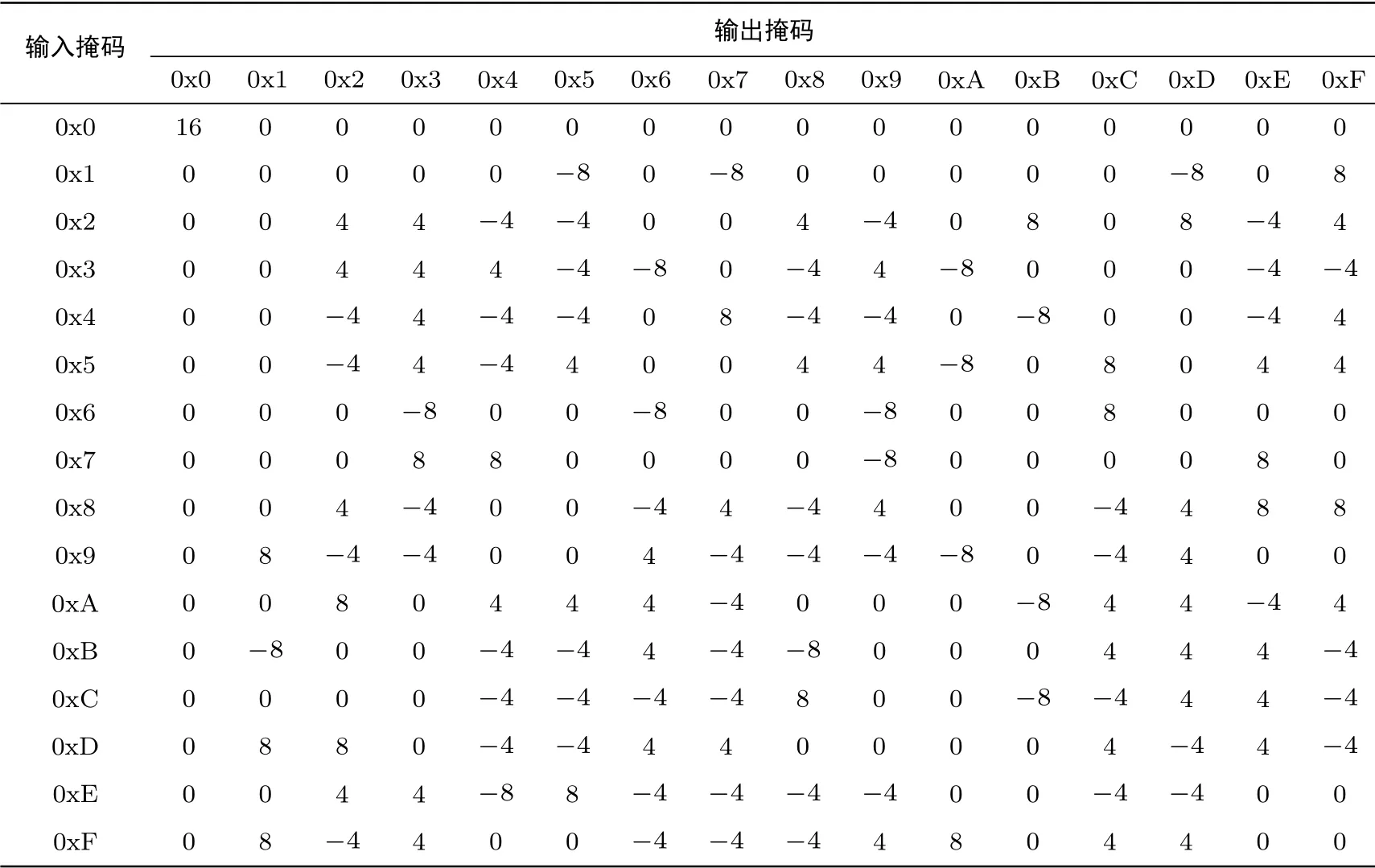
表10 HBcipher 算法S 盒线性逼近表Table 10 Linear approximation table of S-box of HBcipher algorithm
