改进的缩减轮Crypton-256 分组密码算法的中间相遇攻击*

郝泳霖, 田呈亮, 袁 祺

1.密码科学技术国家重点实验室, 北京100878

2.青岛大学计算机科学技术学院, 青岛266071

3.中国科学院信息工程研究所信息安全国家重点实验室, 北京100093

1 引言

分组密码算法Crypton[1]于1998年被Lim 提出, 它也是高级加密标准(Advanced Encryption Standard, AES)的候选算法之一.分组长度128 比特, 密钥长度可变, 最短64 比特, 最长256 比特.在FSE 1999 会议上, Lim 又提出了Crypton 的加强版[2], 对原版的S 盒和密钥扩展方案进行了改进, 命名为Crypton v1.0 (由于本文的攻击方法对Crypton 和Crypton v1.0 都有效, 在没有特别说明的情况下, 我们将两个版本统称为Crypton).虽然Crypton 最终不敌Rijindael[3], 落选AES 标准算法, 但是Crypton 与最终的AES 标准算法有很多相似之处, 学术界对它在单密钥和相关密钥模型下的安全强度进行了相当多的研究.

在相关密钥模型下, Wei 等人给出了9 轮Crypton 的相关密钥不可能差分攻击[4].在单密钥模型下,早在1999年, D’Halluin 就给出了6 轮Crypton 的积分攻击[5]; 2001年又出现了同样轮数的不可能差分结果[6]; 2010年出现了7 轮不可能差分结果[7]; 2013年, Lin 等人给出了7 轮Crypton 的中间相遇攻击[8]; Liu 等人改进了7 轮的攻击结果并将轮数扩展到了8 轮、9 轮[9]; 最近, Li 和Jin 又给出了复杂度更低的8 轮攻击[10].此外, Derbez 等人声称用自动化方法找到了11 轮中间相遇攻击, 但并未提供攻击过程和详细参数[11]; Shakiba 等人还给出了Crypton-256 的Biclique 攻击[12], 可以攻击到全12 轮, 但这种方法需要穷搜全部密钥空间, 并不是一个真正意义上威胁安全强度的密钥恢复攻击.根据以往的攻击结果可见: 中间相遇攻击是对Crypton 最行之有效的攻击方法.

本文关注的是Crypton 在单密钥模型下的中间相遇攻击,详细分析了Crypton 和Crypton v1.0 的算法结构和密钥编排特征.通过构建性质优良的截断差分特征、定制巧妙的密钥猜测方案, 改进了Crypton的中间相遇攻击结果.分析结果表明: 就抵抗中间相遇攻击的能力而言, Crypton v1.0 并不优于Crypton.

中间相遇攻击.中间相遇攻击于1977年被Diffie 和Hellman 提出[13].在过去的十余年中, 中间相遇攻击被广泛运用于对分组密码算法的安全性分析中, 并取得了很好的成果(如文献[14–17]等).特别是对高级加密标准AES, 中间相遇攻击的效率非常高: Demirci 和Selçuk 在FSE 2008 上首次将中间相遇攻击的思想运用于对AES 的安全性分析[18], 给出了对7 轮AES 的攻击结果, 之后经过一系列的改进[19–24], 提出了多重集(multiset)、超级S 盒匹配(super-box)等新思想新技术, 使得攻击轮数逐渐增加, 攻击复杂度逐渐降低.目前, 对AES 最优的密钥恢复攻击结果是由Li 等人给出的[24], 他们构造出了6 轮区分器, 并利用了之前已有的密钥分割技术[23]降低复杂度, 给出了对10 轮AES-256 的中间相遇攻击, 数据/时间/存储复杂度为2111/2253/2211.2.

本文贡献.给出了3 个对Crypton-256 的中间相遇攻击结果.借鉴Li 等人对10 轮AES 的中间相遇攻击[24]的思想, 我们构造了一个6 轮截断差分区分器, 给出了9 轮攻击, 与之前的9 轮攻击结果相比具有更低的时间和存储复杂度; 用同样的6 轮区分器, 我们给出了第一个10 轮中间相遇攻击结果, 数据/时间/存储复杂度为2113/2240.01/2241.59.接着, 利用Crypton 密钥编排性质, 通过巧妙构建密钥过滤方法[23], 提出了10 轮攻击的改进版, 降低了存储复杂度, 改进后的复杂度为2113/2245.05/2209.59.我们将本文的结果与之前所有单密钥模型下的攻击结果进行对比(表1)可见: 我们的10 轮中间相遇攻击是目前对Crypton 可验证的最好的密钥恢复攻击结果(考虑到Derbez 等人[11]声称的11 轮攻击并未给出具体的攻击过程和详细参数, 其正确性不可验证).

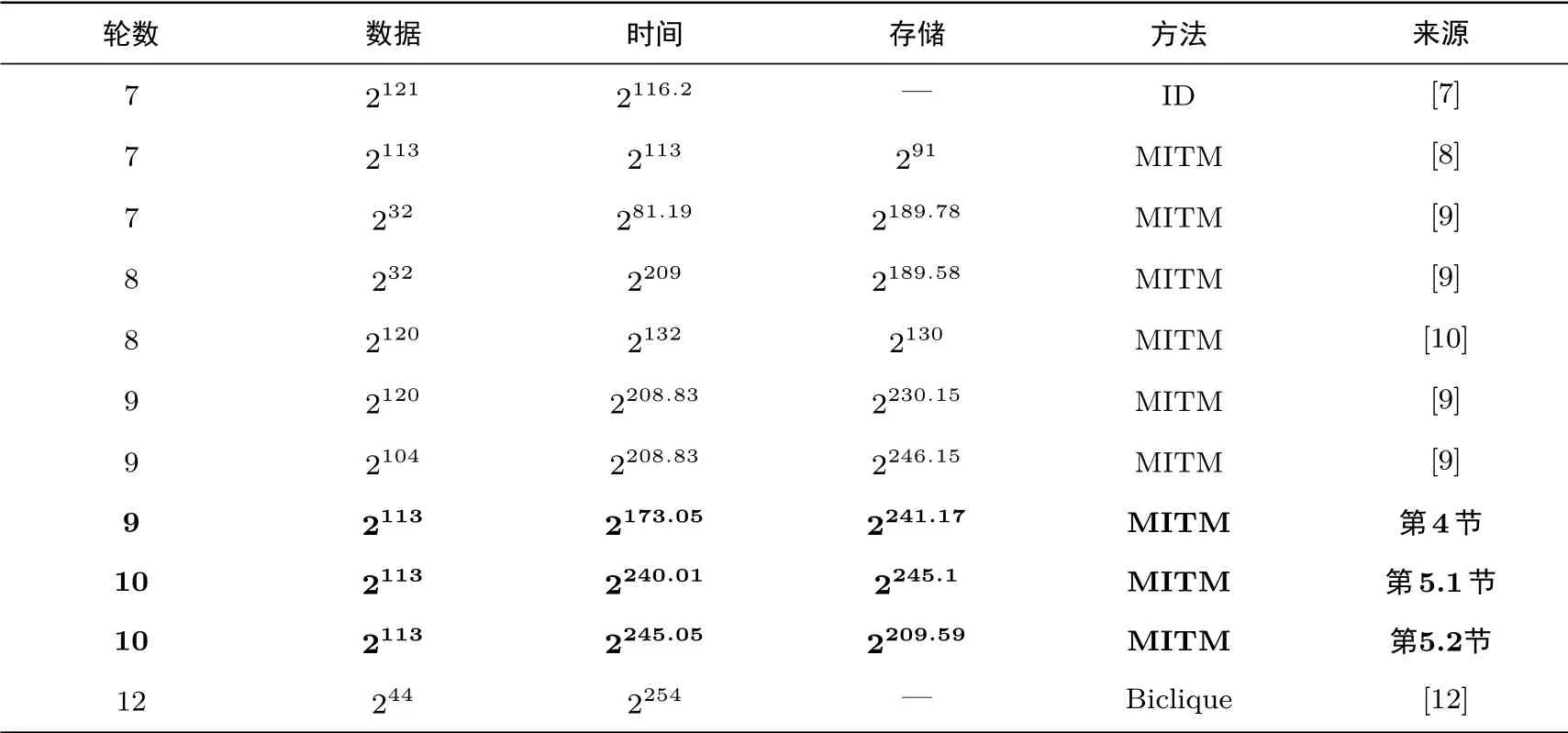
表1 单密钥模型下对Crypton 的密钥恢复攻击Table 1 Key-recovery attacks on Crypton under single-key model

文章结构安排.第2 节简要介绍了Crypton-256 的算法流程和攻击中所需要用到的一些性质.在第3 节构造了Crypton-256 的6 轮区分器, 基于这一区分器, 我们在第4、5 节分别详细描述了针对9 轮、10 轮Crypton-256 的中间相遇攻击, 其中第5 节包含基本攻击和改进攻击两个版本.最后, 我们在第6 节总结全文.

2 预备知识

本节第一部分简要介绍Crypton-256 的算法基本流程, 更多细节请参考原始文献[1,2]; 第二部分介绍中间相遇攻击中需要用到的概念和性质.首先, 对常用的运算的符号做一说明: 按位与(AND)运算用“∧” 表示1在不会引起误会的情况下, 为了使公式简洁, 有时会省略, 如xy 等价于x ∧y.; 按位异或符号为“⊕”; 字符串的级联运算用“∥”.

2.1 Crypton-256 简介

与AES 相同, Crypton 的分组长度为128 比特, 采用SPN 结构进行设计.每个128 比特分组可以看成16 个字节组成的4×4 矩阵, 每个字节的编号如下:完整的Crypton 共有12 轮, 每轮由以下四种变换构成:

非线性代换γ.使用2 个8 比特S 盒S0,S1, 对式(1)的每一个字节进行替换, 其中S0,S1满足关系S0=且具有与AES 的S 盒相同的性质.

性质1 [1]任意给定非零的输入输出差分∆in,∆out∈F28{0}, 则平均只有一个解x ∈F28满足方程Si(x)⊕S(x ⊕∆in)=∆out.

比特置换 π.对式(1)中矩阵A 的每一列进行线性变换, 共有四种可能的线性列变换, 记作π0,···,π3.将A 的第i 列记作Ai= (a4i,a4i+1,a4i+2,a4i+3)T.在偶数轮(2,4,··· ,12)中, π(A)=(π3(A3),π2(A2),π1(A1),π0(A0)), 奇数轮(1,3,··· ,11)中, π(A)=(π0(A3),π3(A2),π2(A1),π1(A0)).由于我们只需要用到列变换 π0的性质, 将 π0的具体运算介绍如下: 令 (b0,b1,b2,b3)T=π0((a0,a1,a2,a3)T), 则

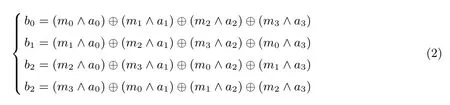
其中m0=0xfc, m0=0xf3, m0=0xcf, m3=0x3f 为常数.通过简单的计算可以得到π0具有性质2.

性质2[24]设(b0,b1,b2,b3)T= π0((a0,a1,a2,a3)T)并令a2= a3= b3= 0, 则a0∥a1共有28个可能值.

π0,··· ,π3的分支数均为4, 具有如下性质3.

性质3[24]在πi的8 个输入/输出字节中, 如果已知其中的5 个, 那么剩下的3 个也可以唯一地确定出来.

置换τ.类似于矩阵转置, 将矩阵中的元素位置做如下变换

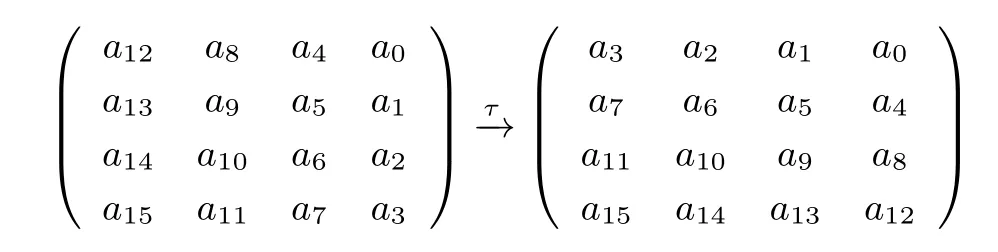
密钥加σ.σK即为令中间状态的16 个字节与密钥K 进行按位异或(XOR)操作, 这与AES 的轮密钥加(AddRoundKey, ARK)是完全一样的.

在加密流程开始之前, Crypton-256 密钥扩展方案会将256 比特的主密钥K 扩展为13 个128 比特的子密钥k0,··· ,k12.

对于轮数r = 1,··· ,12, 我们定义相应的轮函数ρr(·)= σkr◦τ ◦π ◦γ(·), 进一步定义线性变换Φ(·)=τ ◦π ◦τ(·).从而, 由明文P 开始, 通过r 轮Crypton-256 加密得到密文C 的完整流程可以表示为

在加密过程中, 所有的128 比特中间状态(P,C 除外)我们都用小写字母来表示, 我们约定σkr输出的128 比特状态为xr, 而ρr中γ 的输出为yr−1, τ 的输出为wr−1(r =1,··· ,12), 即

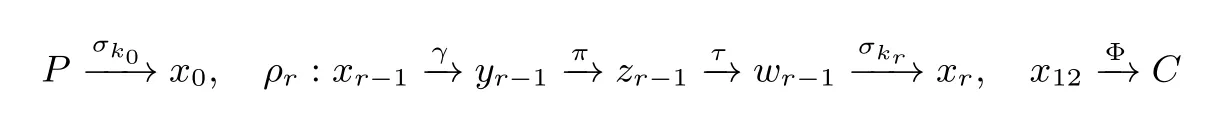
任一状态x 的第i(i ∈[0,15])个字节用x[i]表示, 第i 到j 字节用x[i,··· ,j]表示, 编号与式(1)一致.

密钥扩展方案.对于256 比特主密钥K, Crypton-256 首先对其进行非线性变换, 得到一个新的256比特密钥, 由于这个非线性变换是1-1 映射, 所以我们依然用K 来表示.子密钥k0和k1分别对应K的高位128 比特及低位128 比特, 即K = k0∥k1.然后, 对于i = 1,··· ,6, 子密钥k2i(k2i+1)可以由k2i−2(k2i−1)通过循环移位和与轮常数异或这两种简单的操作而完全确定, 即

性质4[1,2]Crypton-256 的子密钥k0,··· ,k12满足: 对于任意i ∈[0,6](i ∈[0,5]), 知道k2i(k2i+1)就完全可以推出全部的k0,k2,··· ,k12(k1,k3,··· ,k11).而且, 知道k2i(k2i+1)的一个字节, 一定可以唯一确定出k0,k2,··· ,k12(k1,k3,··· ,k11)的一个字节.

性质4 对于Crypton 和Crypton v1.0 都是成立的, 但具体到密钥字节的位置, 二者略有差异, 我们的中间相遇攻击需要利用Crypton 和Crypton v1.0 的子密钥之间的一些具体关系, 分别表述为性质5 和性质6, 这些性质可以帮助我们降低中间相遇攻击的复杂度.

性质 5[1]在 Crypton 中, 已知 k5[0,··· ,7]可以推出 k1[0,7,9,10,11,12,13,14]; 已知k4[4,7,10,13], 可以推出k0[0,··· ,3].

性质6[2]在Crypton v1.0 中,已知k5[0,··· ,7]可以推出k1[2,3,5,7,8,9,12,14];已知k4[2,4,9,15]可以推出k0[0,··· ,3].

2.2 中间相遇攻击相关概念

定义1 (σ 集)[18]一个σ 集是由256 个128 比特中间状态所构成的集合.中间状态的1 个字节取遍全部256 个可能值(称为“活跃字节”), 其余15 个字节取相同的常值(称为“非活跃字节”).

定义2 (超级S 盒)[24]考虑Crypton 加密中的如下流程:

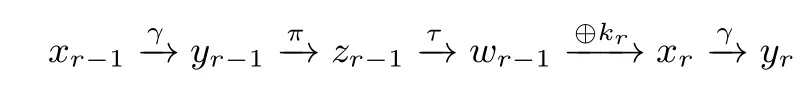
整个过程等价于并行如下4 个超级S 盒SSB0,··· ,SSB3:

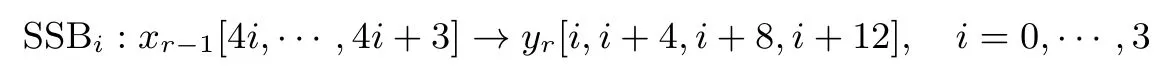
其中超级S 盒SSBi需要知道4 个密钥字节kr[i,i+4,i+8,i+12]才能进行, 它可以看作是32 比特到32 比特的S 盒运算.根据性质1, Crypton 的超级S 盒具也有如下性质7.

性质7[24]给定非零的输入盒输出差分∆in,∆out∈F232{0}, 平均只有一个解满足方程SSBi(x)⊕SSB(x ⊕∆in)=∆out.

3 Crypton-256 的六轮区分器

借鉴之前AES-256 的6 轮区分器构造方法[24], 我们构造了Crypton-256 的6 轮截断差分区分器.根据性质3, 我们可以证明第6 轮中间状态字节满足如下关系

定义字节ein,eout如下

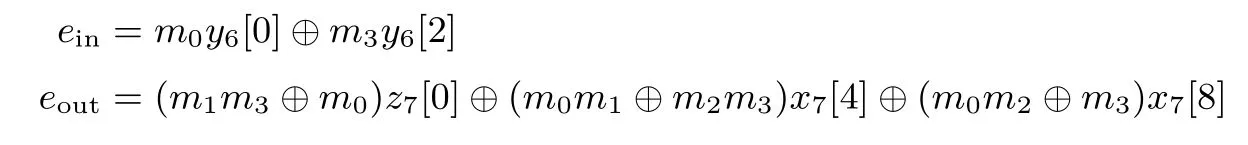
则ein,eout满足关系

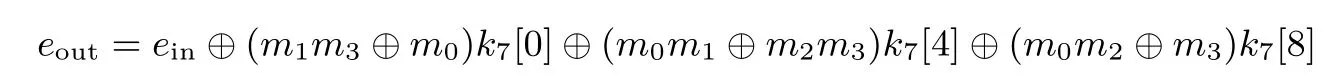
根据性质5 和性质6, 已知k5[0,··· ,7]可以推出k1[12], 因此我们可以构造图1 所示的截断差分区分器, 该区分器对于Crypton 和Crypton v1.0 都有效.(注: 本文所有图中, 黑色表示差分非零的字节, 阴影部分表示需要通过猜测或计算得到的密钥字节).为了证明构造该区分器的存储复杂度上界, 我们证明了如下定理1, 该定理的证明综合运用了高效差分枚举技术[22]和密钥过滤技术[23].

定理1令为w0[12]位置活跃的σ 集且其中的元素满足: 对t ∈[0,255], 有考虑对σ 集的前33 个元素(w0,··· ,w32)进行6 轮加密得到一个256 比特序列如果该σ 集中存在一对元素满足图1 所示的截断差分, 那么对应的256比特序列只有2240个可能的取值.

图1 本文的中间相遇攻击中所使用的6 轮区分器Figure 1 6-round distinguisher used in proposed MITM attacks

证明:首先, 我们要证明: 知道如下46 个字节的信息就可以计算出序列

对于固定的i,我们将任意中间状态的差分xm⊕xi表示为∆xm(m ∈[0,255]).在第1 轮,可以在已知的情况下通过等式显式地计算出来.由于已知, 我们可以根据计算由于可以进一步通过线性变换σk2◦τ ◦π 得到差分[3,7,11,15].类似地, 我们可以在已知[3,7,11,15]的情况下得到由于和都是已知的, 我们可以推出状态值和再通过密钥k4进行1轮加密得到和已知和k5[0,··· ,7], 我们就能得到[0,··· ,7]和[0,··· ,7].又因为k6[0,1]可以通过k4得到(性质4), 我们又可以进一步进行部分加密得到[0,1]和[0,1]最终获得根据式(3), 我们知道对m ∈[1,32]恒成立, 这就证明了式(4).

如果对固定的i 做一限制: wi属于某状态对(wi,wj)满足图1 的截断差分特征.可以进一步证明:只需知道如下式(5)中的33 个字节的信息, 我们就可以确定式(4)的全部信息

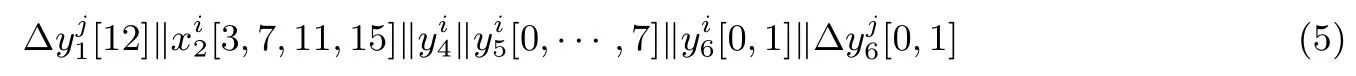
我们从加密方向推导.由于(wi,wj)满足图1 的截断差分传播, 因此知道就足以求解出差分再知道了式(5)的我们就可以计算出并进一步得到差分

4 9 轮Crypton-256 的中间相遇攻击

我们将第3 节的6 轮区分器上扩1 轮, 下扩2 轮, 给出了9 轮Crypton-256 的中间相遇攻击.扩展之后的截断差分特征见图2, 明文对(P,P′)符合该截断差分特征的概率为2−144.攻击过程分为预计算和线上两个阶段, 具体步骤如下.

预计算阶段.在预计算阶段, 我们构建2 个查找表T0,T1.其中T0存储着2240序列及能提高攻击成功率的其他信息; 表格T1可以进一步降低线上阶段的时间复杂度.具体步骤如下:

(1)将T0初始化为空.对全部2128个k4可能值, 我们做如下步骤:

(a)根据k4, 推出k6.

(b)通过以下步骤构建临时查找表T2:

i.对于y5[0,··· ,7]的所有可能值, 根据k6向前计算得到y6[0,1];

ii.根据性质2, 确定出28个∆y6[0,1]值满足:

iii.根据已知信息向后计算得到x5[0,··· ,7]和∆x5[0,··· ,7];

iv.将得到的x5[0,··· ,7]存储在T2(∆x5[0,··· ,7])中; 对于每个∆x5[0,··· ,7](共264个),平均有28可能的x5[0,··· ,7]被保存下来.

(c)再通过以下步骤构建临时查找表T3:

i.对∆y2[3,7,11,15]∥∆x5[0,··· ,7]的全部296个可能值, 推出对应的差分∆x3∥∆y4;

ii.根据性质7 和密钥k4, 我们平均可以得到一个解x3∥y4满足差分条件∆x3∥∆y4;

iii.将x3∥∆x5[0,··· ,7]存储在T3(∆y2[3,7,11,15])分量中, 每个∆y2[3,7,11,15](共232个)对应264个x3∥∆x5[0,··· ,7].

(d)对每个∆y1[12]∥x2[3,7,11,15](共240个), 我们通过查找表T2和T3逐步构建出T0:

i.通过k2推出k4(性质5)并进一步通过部分解密y1[12]∥x1[12];

ii.根据已知的y1[12]和∆y1[12]推出∆x2[3,7,11,15]并进一步根据已知的x2[3,7,11,15]得到∆y2[3,7,11,15];

iii.查询T3(∆y2[3,7,11,15]), 可以平均得到264个对应的x3∥∆x5[0,··· ,7];

iv.对每一个x3∥∆x5[0,··· ,7], 通过查询T2找到对应的28个x5[0,··· ,7].由于k4是已知的, 我们可以从x3加密到w4, 再根据k5[0,··· ,7]得到x5[0,··· ,7];

v.在通过k5[0,··· ,7]推出k1[12]之后, 我们可以通过对y1[12]进行部分解密得到w0[0]从而构建出序列

vi.通过k4推出k0并将字符串存储在表格T0中.

(2)将T1初始化为空, 定义集合λ 如式(6)

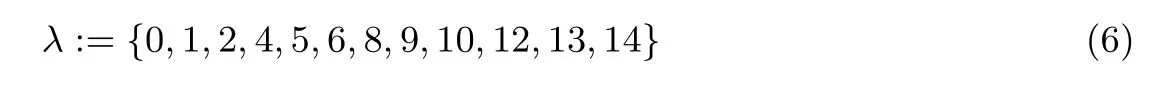
进行如下步骤:

(a)对密钥u9[λ]||u8[0,4,8]全部2120个可能值和的296个可能值, 我们计算相应的eout;

(b)将eout存储在中.

线上阶段.首先要找到满足图2 差分特征的明文对, 从而构造出相应的σ 集, 再进一步通过密钥猜测和部分加解密得到对应的序列最后通过预计算阶段构建的查找表T0确定取遍所有可能值, 其余12 个字节取相同的常值.这样每个结构体中都有个明文对满足截断差分特征的起始部分, 共有281+63= 2144.由于整个截断差分的概率为2−144, 平均有1个明文对满足图2 的要求.

(2)在每个结构体内部选择满足∆C[12,··· ,15]= 0 的明文对, 这是一个32 比特的过滤器, 共有2112个明文对(P,P′)被保留了下来.

(3)对每个保留下来的(P,P′)进行如下操作:

(a)猜测∆w0[12]并假定∆w0[0,4,8]= 0, 从而推出差分∆y0[0,··· ,3], 再结合已知的差分∆x0[0,··· ,3]= ∆P[0,··· ,3], 我们平均可以得到1 个符合上述差分条件的x0[0,··· ,3]∥y0[0,··· ,3](性质1).根据已知的P[0,··· ,3]∥x0[0,··· ,3], 我们进一步推出k0[0,··· ,3];

(b)猜测∆y7[0,1,2]并假定∆y7[3,··· ,15]= 0, 然后线性求出差分∆x8.再根据密文的差分得到∆y8.对于∆x8[λ]∥∆y8[λ], 我们平均可以得到1 个符合差分条件的x8[λ]∥y8[λ](性质1, λ 定义见式(6)); 又根据x9= τ ◦π ◦τ(C)可以线性推出以及密钥

(c)猜测密钥u8[0,1,2], 由于已知k0[0,··· ,3], 我们可以从P 出发得到w0[0,4,8,12].将w0[0]赋值为0,··· ,32, 通过部分解密确定出对应的P0,··· ,P32以及密文C0,··· ,C32; 再通过已知的u9[λ]||u8[0,4,8]和(由密文得到, t = 0,··· ,32), 我们可以获得以及对应的序列

(d)查询T0, 看是不是在T0中, 如果存在, 则u9[λ]∥u8[0,4,8]为正确的密钥; 否则,返回步骤(a); 如果穷举∆w0[0]∥∆y7[0,1,2]∥u8[0,1,2]的全部256个可能值仍未找到正确密钥, 则换一个新的明文对重新开始步骤(a).

(4)在获取了u9[λ]∥u8[0,1,2]之后, 我们穷搜剩余的136 比特密钥u9[3,7,11,15]∥u8[3,··· ,15]从而恢复出256 比特的主密钥K.

复杂度分析.预计算阶段, 构造T2需要28×(8+2)=280次加密; T2包含264+8=272条记录.构造出正确的序列和密钥.具体步骤如下:

(1)构造281个明文结构体并获得它们对应的密文.每个结构体中含有232个明文使得P[0,··· ,3]T3需要296次加密操作, 最终的规模也是296条记录.步骤(d)需要240×28×264×33 ≈2117.05次加密.因此, 预计算阶段的时间复杂度为2128×(280+296+2117.05)≈2245.05; 查找表T0包含2240条记录,每条记录占36 个字节的存储空间, 相当于2240×36/16 ≈2241.17个128 比特分组, 这也是整个攻击的存储复杂度.攻击的时间复杂度由线上阶段的步骤3.(c)决定, 具体值为2112×28×224×224×33 ≈2173.05.数据复杂度为281×232=2113.错误的密钥通过3.(d)的概率仅为2240×2−8×36=2−48, 故该攻击的成功概率为1 −2−48.

图2 攻击9 轮Crypton-256 所用到的截断差分特征Figure 2 Truncated differential characteristics for attacking 9-round Crypton-256

5 10 轮Crypton-256 的中间相遇攻击

将第4 节的攻击向下扩展1 轮就可以得到10 轮Crypton-256 的中间相遇攻击.我们首先在第5.1 节介绍10 轮基本攻击, 然后在第5.2 节介绍10 轮改进攻击.改进攻击通过将基本攻击拆分成多个“弱密钥” 攻击, 从而降低了攻击的存储复杂度, 这一方法之前曾在部分文献中被应用于对AES 的中间相遇攻击[23,24].10 轮攻击的截断差分特征见于图3.

5.1 基本攻击

预计算阶段.10 轮攻击的预计算阶段和9 轮基本是一样的, 只是将9 轮预计算阶段的步骤1.(c).vii替换为如下形式:

• 通过k4推出k10并将存储于T0中;这一变化使得10 轮攻击的成功概率大幅度提升.

线上阶段.10 轮攻击中找到符合图3 截断差分特征的消息对的过程比较复杂, 具体步骤如下:

图3 攻击10 轮Crypton-256 所使用的差分特征Figure 3 Truncated differential characteristics for attacking 10-round Crypton-256

(1)首先构造与9 轮攻击相同的281个明文结构体并获取相应密文, 共得到了2144满足截断差分特征的明文对(P,P′).

(2)对全部2144个明文对(P,P′)进行如下操作:

(a)猜测差分∆y8[λ]并求出∆x9; 通过密文差分∆C 推出∆y9, 对接差分(∆x9,∆x9), 根据S 盒的性质1 平均可以确定出1 个x9∥y9满足差分条件.由于知道了y9和C, 我们可以得到整个k10也就知道了k0(性质4).用k0对明文对部分加密得到∆w0, 如果差分∆w0[0,4,8]0, 则说明之前猜测的∆y8[λ]是错误的, 这是一个24 比特的过滤器.由于∆y8[λ]有96 比特, 所以通过这一步我们共得到了296−24=272个候选的k10及与之相应的k0;

(b)对性质2 中的28个可能的∆y6[0,1]进行部分加密得到∆x7; 再通过已知的k10推出k8.由于∆x7∥k8∥∆y8[λ]都是已知的, 所以根据性质7, 平均可以得到一个解x7[λ]∥y8[λ], 又x9也是已知的, 我们可以恢复出密钥u9[λ]; 用k0对明文P 进行部分加密得到w0, 依次令w0[12]=0,··· ,32, 再部分解密得到σ 集前33 个元素对应的明文P0,··· ,P32和相应的密文C0,··· ,C32;

(c)对(a)中得到的272个k10, 推出相应的k8和等价密钥u8, 根据已知的对密文进行部分解密得到图3 的查询预计算表获得相应的并最终得到序列检测是否在T0中, 如果在, 则继续进行到步骤3.

(3)对于已经得到的密钥u9[λ]∥k10, 穷搜剩余的u9[3,7,11,15]确定出全部256 比特主密钥K.

复杂度分析.预计算阶段的时间复杂度仍为2245.05, T0的中仍然是含有2240条记录, 但每条记录的大小由36 字节增加到48 字节, 因此存储复杂度相应增加到了2240×48/16 ≈2241.59.线上阶段的步骤1 复杂度为232+81= 2113.对于全部2144个明文对中的每一个, 执行步骤2.(a)的复杂度为296; 步骤2.(b)和2.(c)分别为272+8= 280和272+8×33 ≈285.04.因此线上阶段步骤2 的复杂度为2144×(296+280+285.04)≈2240.01.步骤3 的复杂度仅为232.所以, 线上阶段的整体时间复杂度由步骤2 决定, 为2240.01.整个攻击需要232+81= 2113个明文, 所以数据复杂度仍为2113.对于成功概率, 正确的明文对和正确的密钥通过步骤2 的概率为1; 错误密钥通过步骤2.(a)的概率为2−24, 通过2.(c)的概率为2240×2−8×(32+16)= 2−264.因此, 整个攻击的成功概率为1 −2−288.综上, 10 轮Crypton-256 的基本中间相遇攻击的数据/时间/空间复杂度为2113/2240.01/2241.59/, 成功概率高达1 −2−288.

5.2 改进攻击

借鉴之前AES 攻击的方法[23,24], 可以将基本攻击密钥猜测空间划分成若干子空间, 对每个子空间分别进行攻击, 从而降低整个攻击的存储复杂度.而Crypton-256 的密钥扩展方案是线性的, 比AES 更加简单, 更便于我们划分密钥空间, 实现时间和存储的折中.

改进攻击中, 预计算阶段不再构建T0, 只构建T1, 详细步骤见第4 节.线上阶段步骤如下:

(1)与基本攻击(第5.1 节)相同, 通过281个明文结构体获取2144个明文对(P,P′)满足图3 的差分特征.

(2)对232个可能的k4[i0,··· ,i3]分别进行如下步骤:

注:对Crypton[1], 取(i0,··· ,i3)= (4,7,10,13)(性质5); 而对于Crypton v1.0[2], 则取(i0,··· ,i3)=(2,4,9,15)(性质6).

(a)猜测k4的其余12 个字节, 根据已知的k4用第4 节预计算步骤1 的方法构建查找表其中包含了2208个

(b)通过k4求出k0(性质4), 再对281个明文结构体进行部分加密得到w0[0,4,8,12], 并确定出满足∆w0[0,4,8]= 0 的明文对.这是一个24 比特的过滤器, 平均每个结构体有263−24=239个消息对被保留下来, 总共剩余2120个;

(c)通过k4求出k10及等价密钥u10, 对每个结构体中剩余的239个明文对所对应的密文进行部分解密得到并确定出其中符合差分条件的明文对.这是一个32比特过滤器, 平均每个结构体剩余239−32=27个明文对, 共剩余288个;

(d)对全部的288个剩余明文对(P,P′)进行如下操作:

i.通过k4求出k8和k10, 对密文进行部分解密得到x9和∆y8[λ].对∆y6[0,1]的28个可能值(性质2)计算∆x7.由于k8是已知的, 对每个∆x7∥k8∥∆y8[λ]平均可以求得一个x7[λ]∥y8[λ](性质7), 进而可以根据已知的y8[λ]和x9求解出密钥u9[λ];

ii.用k0对明文进行部分加密得到w0, 再通过改变w0[12]的值和部分解密, 获取σ 集前33 个元素对应的明文P0,··· ,P32及其密文C1,··· ,C32;

iii.对t = 0,··· ,32, 我们通过k10∥u9[λ]对密文进行部分解密得到通过查询得到相应的及序列再并进一步计算出差分查询看是否存在, 存在则说明密钥k4∥u9[λ]是正确的.

(3)完成上述步骤之后, 平均只能得到1 个正确的密钥候选k4∥u9[λ], 只需要穷举剩余的232个u9[3,7,11,15]即可恢复全部256 比特主密钥K.

复杂度分析.改进攻击的存储复杂度由决定, 为2208×48/16=2209.59.而构建的时间复杂度是构建T0的2−32,而构建T0的时间复杂度为2245.05,所以构建一个的复杂度2245.05−32=2213.05,所以步骤2.(a)的时间复杂度为232×2213.05= 2245.05, 这也是整个改进攻击的时间复杂度.错误密钥通过步骤2.(e).iii 的概率为2208×2−8×(32+16)= 2−276, 所以攻击的成功概率为1 −2−276.数据复杂度保持不变, 仍为2113.

6 结论

本文借鉴了之前AES 中间相遇攻击的技术[23,24], 通过构造6 轮截断差分区分器, 给出了对9 轮Crypton-256 的中间相遇攻击.与之前的9 轮攻击相比, 我们的结果具有更低的时间和存储复杂度.我们还首次给出了10 轮Crypton-256 的中间相遇攻击结果, 这是目前对Crypton-256 可验证的最好的攻击结果.特别地, 10 轮Cypton-256 的从攻击的时间和存储复杂度上看都略低于10 轮AES-256 的同类攻击, 从一定程度上反映出AES-256 在安全强度上可能略优于Crypton-256.我们的攻击方法对原版Crypton[1]和改进版Crypton v1.0[2]同样有效.