量子访问控制问题的可混淆性*

陈然一鎏, 尚涛, 刘建伟

1.北京航空航天大学电子信息工程学院, 北京100083

2.北京航空航天大学网络空间安全学院, 北京100083

1 引言

混淆(obfuscarion)的概念最早诞生于软件工程, 用于保护软件不被反编译等手段得到程序底层实现逻辑.由于理想的混淆器与密码学中的安全性有形式上的相似之处, 2001年Barak 等人[1]首次将混淆的概念引入密码学, 并提出第一个(同时也是最强的)混淆器的定义: 虚拟黑盒(virtual black-box, VBB)混淆.虚拟黑盒混淆需要满足三个特性, 即(1)功能保持性: 混淆后的线路保留原线路的功能; (2)多项式减缓: 混淆后的线路规模不超过原来线路规模多项式级别的大小; (3)虚拟黑盒性: 通过混淆后线路计算出的所有信息, 一定可以通过对原线路的预言式访问有效计算.同时Barak 也指出, 通用的虚拟黑盒混淆器是不存在的.在通用性无法得到满足的前提下, 混淆理论发展出了一个新的分支, 即对于特定功能的线路的混淆.其中对于点函数的混淆性研究格外引人瞩目[2].2004年Lynn 等人提出了点函数的可混淆性结论[3], 这是首个混淆领域的积极结论.他们指出基于有限自动机和正则表达式的功能是可以被虚拟黑盒混淆的; 2005年Hoeteck[4]在一个稍弱的定义下构造了点函数的标准模型混淆器, 并且指出构造基于强单向置换; 针对多比特输出的点函数, Ran 等人[5]分析了线路的组合问题, 给出了正确的混淆器组合方式;在应用方面, Ran 等人[6]讨论了使用多比特输出点函数混淆在对称加密方向的应用, 指出具有不同属性的混淆器可以用于分别构造满足不同安全性要求的对称加密方案.最新的研究结果包括利用混淆构造可验证可搜索的对称加密方案[7].

量子计算机被证明对某些函数(特别是经典密码学感兴趣的困难函数)有强大的计算能力[8]之后,量子密码学成为密码学家关注的新兴领域.量子混淆的概念最早起源于Scott 的“用量子比特保护线路信息” 的思想[9].严格的量子混淆定义建立在量子计算的理论基础之上.直到2014年之前, 都没有人公开发表过对于量子混淆的研究.在2014年的量子计算通信密码理论会议(Conference on the Theory of Quantum Computation, Communication and Cryptography)上, Alagic 等人[10]首次提出了基于量子拓扑计算的量子混淆器.他们利用辫群的特定高维表达将线路编译成辫, 然后再将其转化成标准形式.但该混淆不符合之前混淆器的定义, 它的应用也未经过严格论证.2016年, Alagic 等人正式提出了量子混淆的定义[11].他们首先定义了量子黑盒混淆器, 并认为量子的黑盒混淆比经典的黑盒混淆更加可行; 随后,Alagic 等人定义了量子不可区分混淆器并且指出了量子混淆器可用于构造量子单向函数、长信息公钥量子加密、公钥量子钱币.2019年, Shang 等人发表了关于量子点函数混淆的研究[12,13].访问控制通过权限规定资源是否可以被访问, 实现对资源的管理, 是信息系统安全的基本要求, 而量子访问控制解决量子计算机相应的问题.目前, 量子密码学中的量子密钥分配、量子安全直接通信等解决通信过程的安全问题,而量子访问控制则按照用户身份及其所归属的用户组来限制用户对量子比特的访问或限制对量子线路的使用, 从而实现对量子计算机系统的资源管理.随着量子信息技术的快速发展, 量子计算机的研究也初现成果[14], 量子访问控制可以逐步应用到量子计算机和量子网络上, 提供有效的资源管理功能, 这一方面的研究成果将对量子密码学的发展提供重要的理论基础.

本文深入研究了以往国内外经典混淆和量子混淆的积极结果, 发展了量子点函数混淆方法, 并基于量子点函数以及基于图的访问控制问题的抽象模型, 定义了量子访问控制问题.通过定义的量子访问控制问题的辅助问题, 解决了量子访问控制问题的可混淆性证明过程中的有效输入指数发散问题, 证明了量子访问控制问题的可混淆性.

本文结构如下.第2 节回顾了量子混淆以及经典的基于图的访问控制问题.第3 节定义量子访问控制问题和量子点函数, 并论证量子访问控制问题的可混淆性.最后, 在第4 节总结全文, 并讨论未来可能的研究方向.

2 相关知识

2.1 量子混淆

Alagic 等人[11]最先明确了量子混淆的定义, 并且完成了一些基础的证明工作.在量子混淆理论中,一个量子线路混淆器按如下方式定义:

定义1(可重复)量子线路混淆器

一个(可重复)线路混淆器满足以下条件:

– (功能保持性)输入n 量子比特的量子线路C, 输出m 量子比特的量子态O(C)满足

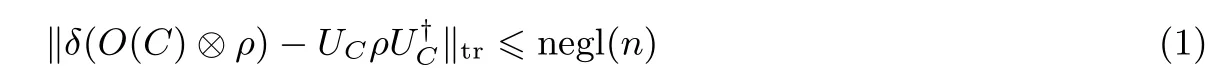
– (多项式减缓)

– (虚拟黑盒性)对任意QPT A, 都有QPT SUC使得对所有的线路C 满足

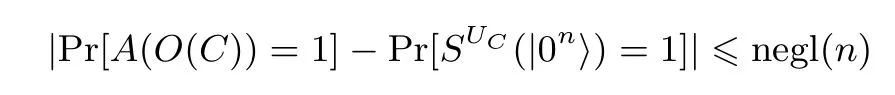
– (可重复)使用δ 后, 功能保持性依然满足.

在式(1)中可以看到,量子混淆与经典混淆最大的不同在于,为了使用户能够完成一些特定的功能[11],量子混淆器的输出不再是一个量子线路的描述, 而是一个量子态.因为混淆器输出的是量子态, 所以解释器δ 是必要的.值得注意的是尽管解释器算法δ 必须是多项式时间的, 混淆算法O 本身并不需要是多项式时间的.在混淆器的实现上要求混淆算法多项式时间可实现, 但在理论上非多项式时间的混淆算法得到的结论更强.定义1 中关于解释器的定义可以有多种形式, 例如对于同一个量子线路族, 可以设置一个共同的量子混淆解释器; 或者混淆算法本身就由一个量子态和一个量子线路构成, 终端用户可以在量子线路上执行量子态和需要的输入.容易证明这两种解释器的定义是等价的, 当其中一种量子混淆器存在时另一种也存在.

本文采用如定义1 所示的量子混淆定义.这里可做一个直观的解释: 混淆算法O 计算线路C 在所有可能的输入下可能得到的输出值, 并记录在O(C)中; 解释器δ 仅起到一个选择的作用, 根据混淆线路的输入, 选择相应的输出.这样尽管混淆算法O 本身可能不再是多项式时间的, 解释器δ 一定是多项式时间的.再次强调解释器是经典混淆器向量子混淆器扩展时自然且必要的补充, 为了使定义有效, 必须存在一个有效的算法来使用O(C)计算UC的功能.无论这个有效的算法是什么, 本文将其定义为解释器, 用δ表示.

另一个量子混淆相较于经典混淆器新引入的性质是可重复性, 显然可重复的量子混淆器要比不可重复的量子混淆器更强, 因为可重复性实际上允许量子敌手拥有更强攻击能力[11].本文中所有的讨论都将基于可重复的量子混淆器.

2.2 基于图的访问控制

基于图的访问控制问题[15,16]中, 安全策略由系统图决定, 系统图由安全策略框架生成.安全策略框架是一个四元组SP = (TG,RS,Pos,Neg).其中, TG 是一个类型图, RS 是规则集合, Pos 是肯定约束,Neg 是否定约束.所有的系统图由类型图根据规则集合变换得到, 并且必须包含肯定约束中的图作为子图,且不得包含否定约束中的图.

一个典型的访问控制系统图如图1 所示.图中U 代表用户, R 代表角色, T 代表任务, t 代表行为.用户到角色的边代表用户与角色的从属关系; 角色到角色的边代表角色之间的从属关系; 角色与任务之间的边代表角色与任务的分配关系; 用户与行为之间的边代表用户与行为的执行关系.系统通过系统图对用户权限进行判定.当用户向系统提出一个行为申请时, 系统根据用户判断所属角色, 并判断申请的任务与角色之间是否有分配关系; 在执行过程中, 由具体的用户来执行任务相应的行为.

图1 典型系统图Figure 1 Typical system graph

3 量子访问控制问题及其可混淆性

3.1 量子访问控制问题的定义

如前文所述, 一个基于图的访问控制系统依据系统图进行各种操作.系统图中的信息可以被再次抽象.图中的节点可以是用户、角色、任务、行为, 统称为节点秘密; 图中的边可以是用户与角色的从属关系、角色与角色的阶层关系、角色与任务的分配关系、用户与行为的执行关系, 统称为邻边口令.节点秘密和临边口令以量子态的形式存储.在系统执行过程中, 用户向系统提出一个行为申请, 在图上反映为从当前节点前进到目标节点: 当且仅当该用户能够提供两个节点之间的临边口令时, 系统接受该申请, 并返回目标节点秘密.

量子访问控制问题包括图的拓扑结构、邻边口令以及节点秘密.对量子访问控制问题的安全混淆要求隐藏量子访问控制问题的全部信息, 包括图的拓扑结构、所有的临边口令以及节点秘密.本节给出访问控制问题的形式化定义.

定义2量子访问控制问题

一个基于图的量子访问控制问题XG定义如下:

(1)考虑一个具有k 个节点的有向图G.每个节点u ∈k 有最多d 个有序邻边(注意可能存在多条邻边指向同一个节点的情况), 定义E ={(u,v,i):v =} 为所有邻边的集合.

那么

注意到量子访问控制问题在形式上与经典的点函数有相似之处.这启发我们从量子点函数的可混淆性入手, 研究量子访问控制问题的可混淆性.

3.2 量子访问控制问题的可混淆性

3.2.1 量子点函数和量子多点函数的可混淆性

定义3量子点函数

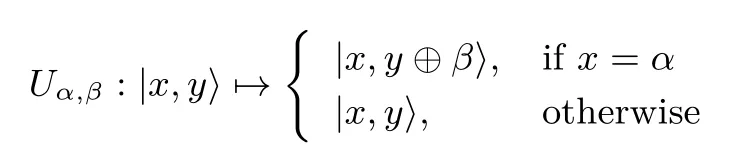
其中α,β ∈{0,1}n.

设功能Uα,β由某个特定的线路Cα,β实现.定义Cn={Cα,β:α,β ∈{0,1}n}, 以及

量子点函数在随机预言模型下是可混淆的.使用文献[17]中定义的量子随机预言机(QRO)Rq:其中R:{0,1}2n{0,1}2n.按如下方式构造一个点函数Uα,β的混淆: OR(Uα,β)随机选取访问随机预言机Rq并得到结果其中R1, R2分别是R 的前n 个和后n 个比特(即随后, 丢弃寄存器|α,将保存下来; 然后对于输入以访问随机预言机Rq得到结果并保存下来; 最后OR(Uα,β)比较是否有R1(r,x)= R1(r,α), 如果是则输出否则输出

定义4一般输出的量子多点函数

其中αi,βi∈{0,1}n.设功能U(α1,β1),···,(αt,βt)由某个特定线路C(α1,β1),···,(αt,βt)实现.定义αi,βi∈{0,1}n}, 以及

C∗的可混淆性可以通过将C∗中的每个元素视作C 中元素的结合来证明.下面证明C∗是可混淆的.

引理1量子线路族C∗是可混淆的.

证明:考虑结合线路{C1#···#Ct:Ci∈C}.线路有输入两个寄存器(一个log k 位的控制位寄存器和一个n 位的输入位寄存器), 在第一个寄存器的值的控制下, 将第二个寄存器应用在对应的量子线路上.即

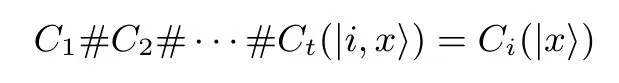
首先Ci是可混淆的, 于是存在O(C1),O(C2),··· ,O(Ct).由于t 是n 的多项式级别, 线路O(C1)#O(C2)#···#O(Ct)中任意两个混淆器使用同样的r 的概率是可忽略的.因为混淆器是随机算法, 在所有的r 都不相同的情况下, 对C1#C2#···#Ct具有预言式访问的模拟器可以模拟任意获得O(C1)#O(C2)#···#O(Ct)的敌手.因此O(C1)#O(C2)#···#O(Ct)是一个对C1#C2#···#Ct的有效混淆.

考虑对C1#C2#···#Ct具有预言式访问的线路MC1#C2#···#Ct.M 按如下方式工作: 对任意输入ρ,M 将|ρ,0输入C1, 得到再依次得到最后返回显然M = C(α1,β1),···,(αt,βt).那么将C1#C2#···#Ct替换为混淆O(C1)#O(C2)#···#O(Ct)并置于M 内部, 得到的也是的有效混淆.即是可混淆的.

3.2.2 量子访问控制问题辅助问题的可混淆性

利用C∗和引理1可以证明量子访问控制问题的可混淆性.但存在以下问题: 有向图中有k 个节点,所以nk; 最坏的情况下, 问题XG可能会有dk种有效输入(输出不为0 的输入), 而C∗对t 要求t=ploy(k), 所以不能直接证明该问题可混淆.

为解决规模的指数发散问题, 引入如下访问控制问题的辅助问题.

定义5辅助问题

该定义下的访问控制问题最多只有kd 个有效输入(输出不为0 的输入).定义问题WG(u,z,i,x), 对于v ∈[k], 随机选取κu←{0,1}k, 对于输入(u,z,i,x)返回定义

由引理1可知辅助问题W 可混淆.显然, 这个混淆器的安全性并不会因为引入的“密钥” κ 而有所降低, 因为除非敌手经历过节点v, 否非他不会得到任何有关κv的信息.而经历节点v 的唯一条件是易知邻边上的口令πe.

3.2.3 量子访问控制问题的可混淆性

现在通过证明量子访问控制辅助问题的可混淆性证明量子访问控制问题是可混淆的.

定理1量子线路X 是可混淆的.

证明:首先, 论证量子访问控制问题和辅助问题的关系.任取XG∈X, WG∈W, 存在线路M 使得且存在线路N 使得按如下方式工作: 对于输入M 以访问WG,如果WG返回则以访问WG, 如此继续直到其返回⊥或者完成所有输入得到不论何种情况输出返回的结果.N 按如下方式工作: N 在内部维护两个表: 一个用于存储“密钥”κi, 一个用于存储经历过的邻边以及邻边口令.初始化时设其他的“密钥” 置为⊥.对于输入|u,z,i,x, N 检查是否有z = κu⊥, 如果是则说明N 已经记录了节点1到节点u 的路线, 将其发送给XG.如果XG返回了v,σv, N 还要检查是否已经分配了κv, 如果不是则随机选择“密钥” 并分配给节点v.注意N 模拟WG成功的前提是在N 经历节点u 的领边e之前没有以有效的口令和“密钥”访问过u 和e, 而该事件的概率是可以忽略的, 所以满足

其次, 利用M 和N 构造XG∈X 的混淆.

由于W 是可混淆的, 设O(WG)是W ∈W 的一个混淆.构造线路按如下方式运作: 首先它将输入传给M; 然后每当M 需要以ρ 预言式访问WG时, M′计算δ(O(WG)⊗ρ)并返回给M; 最后输出M 的输出值.

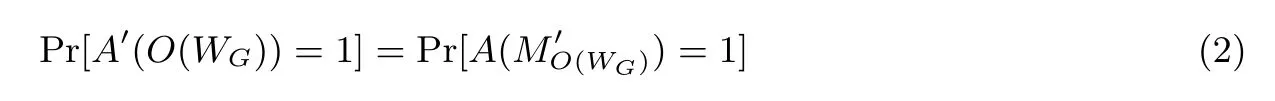
又因为混淆O(WG)满足虚拟黑盒性质:

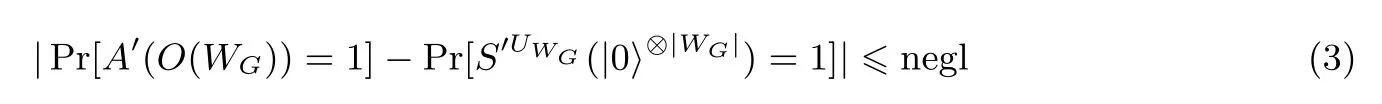
接下来通过S′UWG 构造SUXG.SUXG 按如下方式运作: SUXG 得到输入后, 将传给S′UWG; 每当S′UWG 需要以ρ 预言式访问UWG时, SUXG 计算并返回给S′UWG; 最后输出S′UWG 的输出值.这样, 有

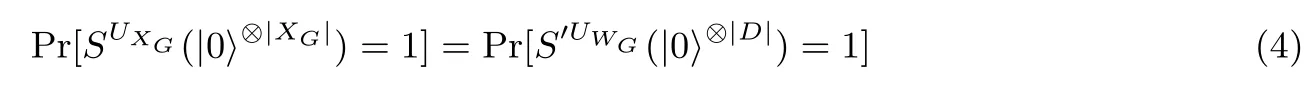
4 总结

本文在Alagic 等人[11]工作的基础之上补充了量子混淆理论的关键引理和概念.本文给出了在量子随机预言模型下的一个可混淆的函数族: 量子点函数, 证明了量子多点函数的可混淆性.本文定义了量子访问控制问题, 通过量子访问控制问题的辅助问题给出量子访问控制问题的可混淆性证明.

相较于密码学的其他领域, 混淆理论的独特性和重要性是不言而喻的; 与此同时, 量子通信和量子计算在本世纪也得到了长足的发展.本文将混淆理论与量子密码学两个前沿方向相结合, 是对量子密码学理论基础的重要补充.

对量子混淆理论的研究目前甚少, 主要的研究方法还是沿袭经典混淆理论的研究轨迹, 将经典混淆理论的结果扩展到量子情形.本文认为, 量子混淆未来的研究重点有以下几项:

(1)信息论安全的量子黑盒混淆器的量子力学机制实现以及用户对混淆量子态多项式次数的使用.这样的量子混淆器将非常强力, 也将成为量子力学在密码学领域能发挥更大作用的有力佐证.

(2)对经典线路的量子混淆.因为经典线路的输出是经典比特串, 所以这样做的巨大好处是可以用量子态进行经典计算, 保留经典输出之后通过逐一撤销酉门还原原来的混淆结果, 可以使混淆结果多次使用.

(3)不可重复使用的量子混淆.在现实中经常需要混淆器的输出不能被复制.Broadbent 等人曾讨论过量子一次程序[18], 这也将在密码学中发挥重要作用.

(4)量子随机预言机的删除.量子随机预言机相对于经典随机预言机, 针对叠加态提问做出了大量调整.而量子混淆输出的量子态也可以是叠加态.如何利用量子混淆机制删除量子随机预言机将成为量子密码学可证明安全的研究热点.