同心圆锥曲线中两个命题的证明

广东省佛山市乐从中学(528315) 林国红

一、同心圆锥曲线

定义如果两个圆锥曲线有着公共的焦点F，且与F 相应的准线f 也是公共的，则称这两个圆锥曲线为同心圆锥曲线.

当椭圆和抛物线有着公共的焦点F，且与F 相应的准线f 也是公共的，那么这样的椭圆和抛物线就是同心圆锥曲线.

本文讨论的是椭圆和抛物线为同心圆锥曲线的情形.

二、同心圆锥曲线的两个命题

命题1如图1，设椭圆和抛物线为同心圆锥曲线，F 和f 分别为它们的公共焦点和对应的公共准线，过抛物线上一点A 作椭圆的两条切线，切点为M,N，则FA 平分∠MFN.

命题2如图2，设椭圆和抛物线为同心圆锥曲线，F 和f 分别为它们的公共焦点和对应的公共准线，过椭圆上一点M 作椭圆的切线，且切线交抛物线于A,B 两点，则FM 平分∠AFB.

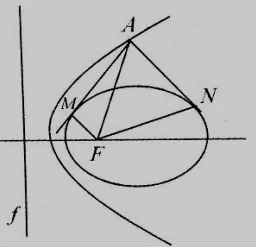
图1

图2

三、两个命题的解析几何角度证法

(1)命题1 的证明

下面证明(∗)式成立.由于

所以(∗)式成立，即FA 平分∠MFN.

(2)命题2 的证明

评注①要证明FA 平分∠MFN，比较容易想的方法是向量的夹角：

虽然式子的两边有对称性，但由于存在x0x1,y0y1,+等不好处理的式子，根据x1+x2,x1x2,y1+y2,y1y2及点A(x0,y0)在抛物线上等已知条件，运算相当复杂，很难证明以上等式成立.②从证明过程可以看出，解析法的运算量较大.

四、两个命题的平面几何角度证法

(1)命题1 的探究与证明

对于命题1，经探究发现，其实并不需要“点A 在抛物线上”这个条件，也就是说可以将命题1 改为更一般性的结论：

性质1设P 为椭圆外一点，过P 点作椭圆的两条切线，切点为P1,P2，F 为椭圆的焦点，则PF 平分∠P1FP2.

性质1 的证明，要用到圆锥曲线的光学性质，先给出三个引理：

引理1从椭圆的一个焦点处发出的光线照射到椭圆上，经椭圆反射后，反射光线通过另一个焦点，且经过反射点的镜面所在的直线为椭圆的切线.

引理2从双曲线的一个焦点处发出的光线照射到双曲线上，经双曲线反射后，反射光线的反向延长线通过另一个焦点，且经过反射点的镜面所在的直线为双曲线的切线.

引理3从抛物线的焦点处发出的光线照射到抛物线上，经抛物线反射后，反射光线平行于抛物线的轴，且经过反射点的镜面所在的直线为抛物线的切线.

这三个引理分别描述了椭圆、双曲线、抛物线的光学性质.其证明读者可参阅文[2].

图3

性质 1 的证明如图3.设 F1,F2是椭圆的两个焦点， 椭圆的长轴长为2a.分别作F1,F2关于切线PP1,PP2的对称点Q1,Q2，连结PQ1,PQ2,P1Q1,P2Q2,PF1,PF2,P1F1,P2F2,Q1F2,Q2F1.易知△PQ1P1∼= △PF1P1， 即得∠PQ1P1= ∠PF1P1①，Q1P1= F1P1， PQ1= PF1.同时△PQ2P2∼= △PF2P2，PQ2= PF2.由引理1， 可得Q1,P1,F2在同一直线上， 且Q2,P2,F1在同一直线上， 所以Q1F2= Q1P1+ P1F2=P1F1+ P1F2= 2a， 同理Q2F1= 2a.所以△PQ1F2∼=△PF1Q2， 可得∠PQ1F2= ∠PF1Q2②.由①， ②， 有∠PF1Q2= ∠PF1P1，即PF1平分∠P1F1P2;同理，即PF2平分∠P1F2P2.所以，回到命题1，即有FA 平分∠MFN.

(2)探究延伸，类比性质

我们知道，很多时侯圆锥曲线间有可类比的性质，这体现圆锥曲线性质的内在统一的和谐美.那么双曲线，抛物线是不是也具有性质1 类似的结论呢? 经进一步的探究，发现在双曲线，抛物线中有性质：

性质2设P 为双曲线外一点， 过P 点作双曲线的两条切线，切点为P1,P2，F 为双曲线的焦点，若切点P1,P2在双曲线的同一支时， 则PF 平分∠P1FP2(如图4); 若切点P1,P2不在双曲线的同一支时，则PF 平分∠P1FP2的外角(如图5).

图4

图5

性质3设P 为抛物线外一点，过P 点作抛物线的两条切线，切点为P1,P2，F 为抛物的焦点，则PF平分∠P1FP2.(如图6)

图6

对于性质2 与性质3，可以用引理2，引理3 并参照性质1 的过程来证明，具体的证明留给有兴趣的读者.

(3)命题2 的探究与证明

命题2 的证明要用到下面两个引理：

引理4若抛物线的焦点为F，抛物线的弦AB 延长后交准线l 于K，则FK 平分FA 与FB 夹角的外角.

证明如图7.分别作AM⊥l,BN⊥l， 垂足为M,N.由AM⊥l,BN⊥l， 易得△AKM ～△BKN， 即有由抛物线的定义， 有AM = AF,BN = BF， 故有由三角形的外角平分线定理的逆定理， 可得FK 平分∠BFG，即FK 平分FA 与FB 夹角的外角.

图7

图8

引理5若椭圆的焦点为F，椭圆的弦AB 延长后交对应的准线l 于K，则FK 平分FA 与FB 夹角的外角.

证明如图8.分别作AM⊥l,BN⊥l， 垂足为M,N，设椭圆的离心率为e.由AM⊥l,BN⊥l， 易得△AKM ～△BKN， 即有由椭圆的第二定义， 有即得故有由三角形的外角平分线定理的逆定理，可得FK 平分∠BFG，即FK 平分FA 与FB 夹角的外角.

图9

命题2 的证明如图9.在抛物线中，由引理4，可知FK 平分FA 与FB 夹角的外角，即FK 平分∠AFG，所以有∠AFK = ∠KFG，在椭圆中，由引理5， 可知FK 平分FC 与FD夹角的外角， 即FK 平分∠CFH， 所以有∠CFK = ∠KFH， 而∠AFC = ∠CFK - ∠AFK，∠GFH = ∠KFH -∠KFG，故有∠AFC = ∠GFH，又因为∠GFH = ∠BFD，所以∠AFC = ∠BFD.于是当C,D重合变成切点M 时(如图2)，即有∠AFM =∠BFM，所以FM 平分∠AFB.

评注①命题2 的证明用到了两个引理，其实在双曲线中，也有类似的性质，即

引理6若双曲线的焦点为F，双曲线的弦AB (或延长后)交对应的准线l 于K，如果点A,B 在双曲线的同一分支上，则FK 平分FA 与FB 夹角的外角;如果点A,B 在双曲线的不同一分支上，则FK 平分FA 与FB 夹角.

②相比较而言，从平面几何角度证明的运算量要少得多，过程简洁，易于理解.

五、命题证明后的反思

(1)数学运算素养包括理解运算对象、探究运算方向、选择运算的方法、设计运算程序、求得运算结果等等.运算是解析几何题型一项重要的考查内容，其解答过程中往往伴有较大的运算，所以合理选择运算方法最为重要，选对方法，才可以简化运算，缩短解题的长度，提高解题效率.

(2)解析几何是用代数方法研究几何问题，其思路直接明了，同时由于代数运算复杂，往往使很多学生对解析几何题望而生畏.实质上解析几何问题本质是几何问题，它们本身就包含一些重要的几何性质，例如圆锥曲线的定义及其光学性质本身就是极其重要的几何性质.如果我们能挖掘出题目里面蕴含的平面几何元素，充分利用平面几何知识，往往可以避开繁琐的代数运算，使解决问题的过程得到简化，解法简洁优美，更好地揭示这些问题的几何性质.因此对于解析几何问题，不应一味地运用解析法，而应该将解析法与平面几何方法相结合，用充分的思考引领认真的计算，从而得到解决问题的最优解法，这不仅是解决解析几何问题，减少运算量的法宝，还可以更好地提高解题能力.

(3)圆锥曲线具有很多统一或相似的性质，圆锥曲线题目往往能引申出多个结论，它的延伸、推广，可以呈现出丰富多彩的数学内容，深刻反映了数学独特的无穷魅力，值得我们去寻找、发现和欣赏.数学家波利亚曾说过“一个有意义的题目的求解，为解此题所花的努力和由此得到的结论和见解，可以打开通向一门新的学科，甚至通向一个科学新纪元的门户”.因此，在平常学习中，我们要有意识加强对圆锥曲线性质的推导与证明，对题目进行适当的发散研究，探索隐藏在题目背后的奥秘，将研究的问题引向深入，挖掘题目的真正内涵，能够找到解决这个问题与解决其它问题在思维上的共性.这样我们才能领会到试题命制的深刻背景，真正做到触类旁通，举一反三，从而达到做一题会一类，甚至会一片的目的，最终让学生在解题思路上产生质的变化，使思维得到发展.