橡胶弹簧结构强度分析及参数优化

丁智平， 曾家兴,， 林 胜， 黄友剑

(1.湖南工业大学 机械工程学院，湖南株洲 412007； 2.株洲时代新材料科技股份有限公司，湖南 株洲 412007)

随着轨道交通的迅猛发展，人们对车辆的安全性、舒适性和可靠性的要求越来越高。橡胶弹性减振元件因其具有良好的减振、隔振性能而广泛应用于轨道车辆减振系统中，起牵引、悬挂、隔振和缓冲的重要作用。但是橡胶弹性元件在使用过程中工况复杂，受到复杂应力和冲击载荷的作用，其刚度特性及疲劳寿命受到很大影响。所以在橡胶弹性元件设计过程中，刚度及疲劳寿命都是设计人员关注的重点。

目前，国内外已有不少学者对橡胶弹性元件的刚度、疲劳以及优化进行了研究。李志超[1]利用ABAQUS软件，以最小化最大应变能密度为目标函数，对平板橡胶堆进行形状优化，提高了橡胶堆的疲劳寿命。丁智平等[2]利用连续介质损伤力学概念，建立疲劳寿命预测模型，对轨道交通用橡胶球铰进行寿命评估，并通过橡胶球铰台架疲劳试验进行验证，预测精度比较理想。Mars等[3]、Saintier等[4]、Verron等[5-6]和Ayoub等[7]进行了一系列的橡胶疲劳研究工作，并提出了多种描述橡胶多轴疲劳的损伤参量。谭高询等[8]结合优化算法以橡胶悬置几何参数为变量，三向悬置刚度曲线为目标，完成橡胶悬置结构设计，并提出一种新的橡胶悬置结构设计方法。张亚新等[9]提出基于等应力设计理念的优化设计，实验结果表明，通过等应力理念设计的产品结构，在确保结构获得等应力的同时，结构的疲劳寿命得到了成倍增加。王伟等[10]对平衡悬架橡胶弹簧静刚度特性进行了分析，并对其极限工况下的内部应力分布进行分析，根据分析结果对现有橡胶弹簧结构进行了结构优化，优化结果理想。赵建才等[11]利用遗传算法和神经网络相结合的策略对橡胶悬置元件的几何结构参数进行优化。王俊等[12]对轨道车辆某型橡胶一系弹簧进行了结构优化。Zhao等[13]对汽车轮子曲轴用橡胶堆的疲劳裂纹问题进行了理论计算和试验分析，发现应力集中区域为橡胶和金属的接触面，并通过改进内套的结构和橡胶胶料硬度，有效的减小了橡胶和金属接触面的应力，提高了产品的疲劳寿命。Lee等[14]考虑橡胶制作的光电隔离器的动态和静态行为特性，采用拓扑优化对光电隔离器进行了优化设计。

本文针对一款新型的锥形橡胶弹簧，选取影响其刚度及疲劳寿命的结构参数，通过正交试验分析各参数对其刚度及最大主应变的影响程度，建立优化模型进行寻优求解，获取最优结构参数。

1 锥形簧结构及工作特性

锥形橡胶弹簧在实际工作中主要承受垂向载荷，同时还能承受一定的横向载荷，起弹性支撑和定位作用，其主要由芯轴、橡胶、隔板和外套组成，见图1。

锥形簧的承载特性为压、剪复合作用，一方面通过橡胶的剪切效应提供大的变形效果，另一方面通过橡胶的压缩效应提供一定的非线性承载能力，从而使得变形与承载达到一个较好的匹配。为提高锥形簧结构的可靠性及承载能力，通常将其设计为多层橡胶压剪复合结构，这种多层结构具有良好的承载特性[15]，承载性能和疲劳性能见表1[16]。

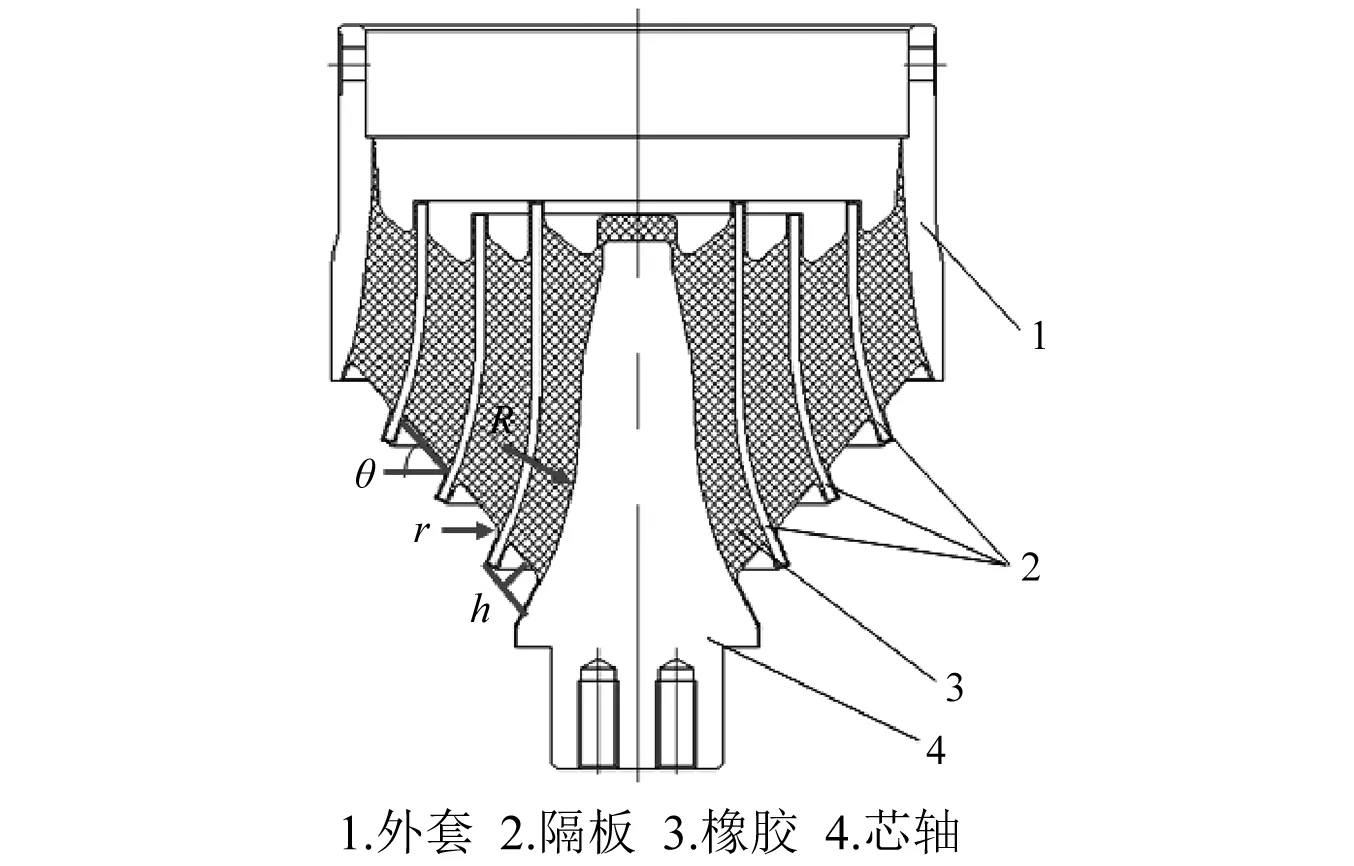
图1 锥形簧结构图

项目工况载荷/kN性能要求垂向刚度/(kN·mm-1)22～300.7(1±12%)疲劳性能(循环次数)30±9kN2000000

2 橡胶材料的本构关系

橡胶材料是一种典型的超弹性材料，具有明显的非线性特征，通常采用应变能密度函数来准确描述其应力-应变关系。橡胶材料的应变能密度函数W是变形张量不变量I1、I2和I3的函数。

(1)

式中：λ1、λ2和λ3为3个主拉伸比。橡胶材料为各向同性几乎不可压缩材料，故λ1λ2λ3=1。W可用变形张量不变量的级数形式表示

(2)

式中：Cij为常数。

表示W广泛采用的是Mooney-Rivlin模型，其表达式为

W=C10(I1-3)+C01(I01-3)

(3)

该模型能很好的描述橡胶在150%内变形的特性。本文在有限元分析中取模型参数为：C10=0.312，C01=0.087[17]。

3 锥形簧结构强度及其影响因素分析

3.1 锥形簧仿真分析

根据图1所示的锥形簧结构，建立如图2所示的轴对称有限元分析模型，根据锥形簧的实际工况载荷，在芯轴一端施加固定约束，在外套沿Y方向施加30±9 kN的载荷。有限元分析结果如表2所示。

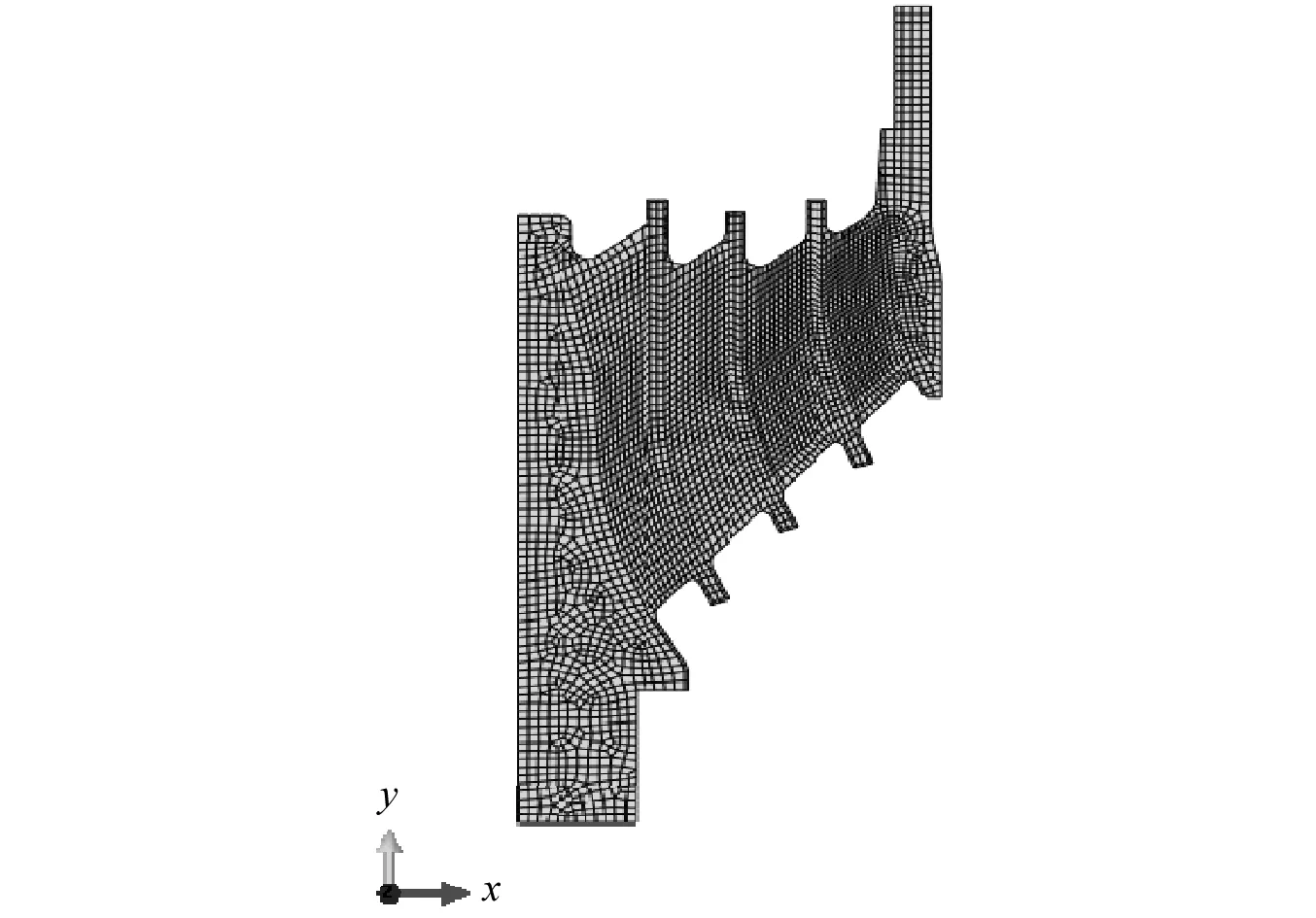
图2 有限元分析模型

项目刚度/(kN·mm-1)最大主应变范围ΔLE分析结果0.6480.6182

文中最大主应变范围是指最大载荷工况下橡胶的节点主应变场数值与最小载荷工况下橡胶的节点主应变场数值之代数差的绝对值中的最大值。

3.2 结构强度影响因素分析

根据锥形簧的结构特点和仿真分析，作者考虑大圆弧半径R、凹槽深度h、型面倾角θ和小圆弧半径r为其结构强度的影响因素，见图1。四个因素初始值分别为：R=150 mm，h=11.3 mm，θ=50°，r=4.5 mm。

本文采用正交试验法研究四个因素对锥形簧结构强度的影响程度。正交试验设计方法的优点有：①因子水平均衡搭配，数据点分布均匀；②大大减少了试验分析次数；③可用相应的极差分析方法、方差分析方法、回归分析方法等对试验结果进行分析，得到有价值的结论[18]。分别对四个因素均匀取4个水平，如表3所示。

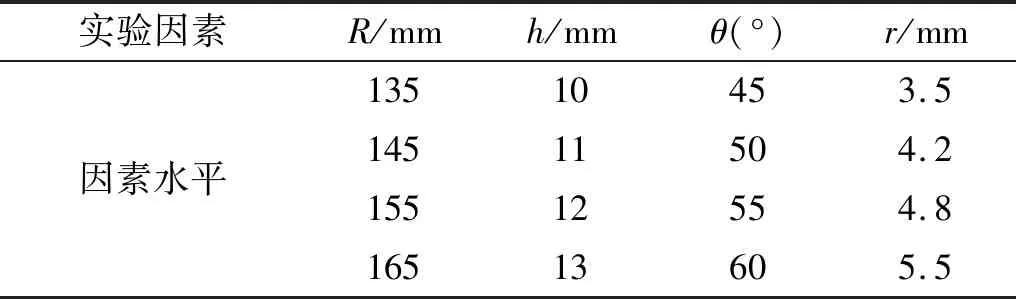
表3 试验因素及水平Tab.3 Factors and levels of simulation test

由表3可知，正交试验为4因素4水平，本文选用L16(45)正交表设计确定了16组试验，进行了锥形簧仿真试验，试验结果如表4所示。表4中第5列未安排试验因素。

为了分析各个因素对锥形簧刚度和最大主应变范围的影响程度，确定各个因素对弹簧刚度及危险单元最大主应变范围影响的贡献率，对表4正交试验结果进行方差分析。所得四个因素对锥形簧刚度和危险单元最大主应变范围影响的方差分析结果见表5和表6,表中F值是指因素平方和与误差平方和的比值。

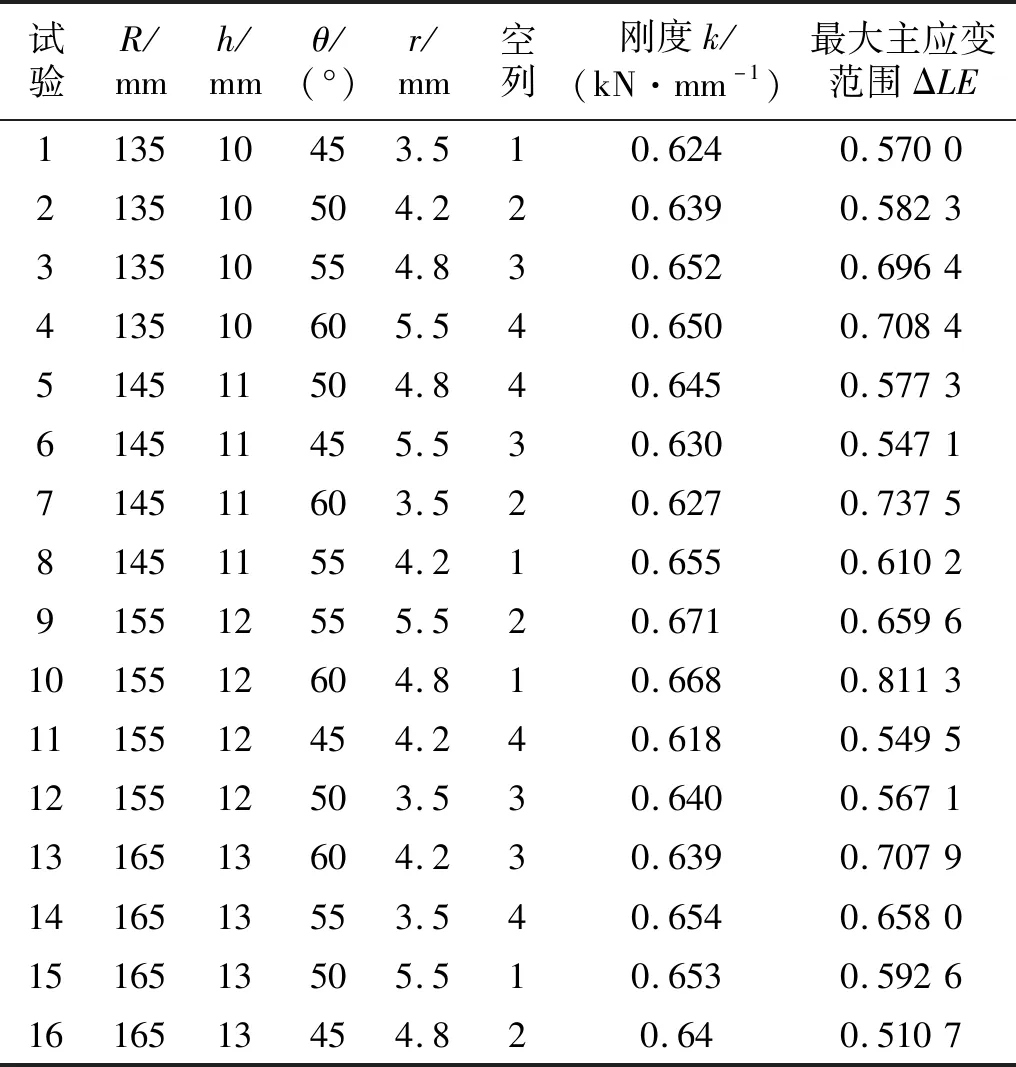
表4 正交试验结果Tab.4 Result of orthogonal test

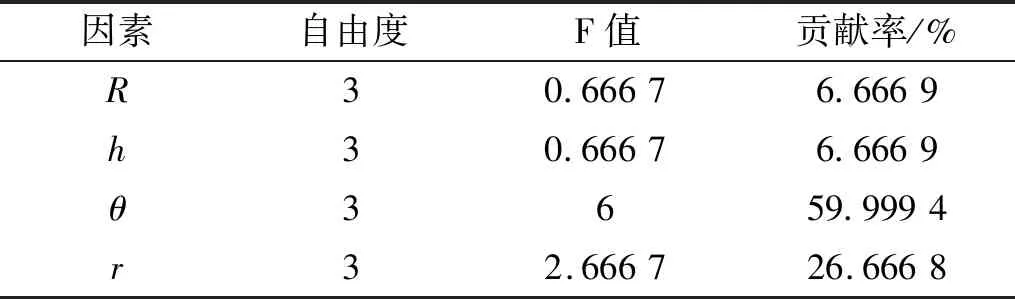
表5 各影响因素对锥形簧刚度影响的方差分析结果Tab.5 The variance analysis results of the influence factors on the conical spring stiffness

表6 各影响因素对最大主应变范围影响的方差分析结果Tab.6 The variance analysis results of the influence factors on the conical spring maximum principal strain range

各因素对刚度和最大主应变范围的影响情况见图3和图4，图中平均数指的是同一水平下试验指标之和与该水平下试验次数之比。

分析表5和表6的数据可知:型面倾角θ和小圆弧半径r对锥形簧刚度的影响较大，贡献率分别为59.999 4%和26.666 8%，大圆弧半径R和凹槽深度h对刚度的影响较小；型面倾角θ对锥形簧危险单元最大主应变范围的影响最显著，其贡献率为88.6848%，大圆弧半径R、凹槽深度h和小圆弧半径r对危险单元最大主应变范围的影响较小。根据图3和图4也可看出，型面倾角对刚度和最大主应变范围的影响最为显著。

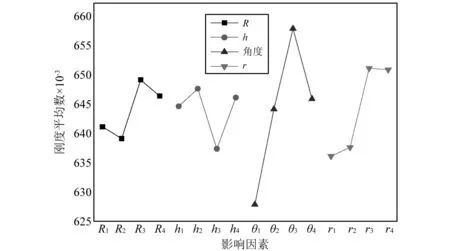
图3 各因素对刚度的影响情况

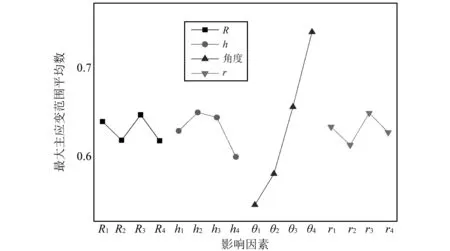
图4 各因素对最大主应变范围的影响情况

4 锥形簧结构参数优化

为了优化锥形簧结构参数，使锥形簧在满足刚度要求的前提下，其最大主应变范围最小，本文利用近似模型方法建立优化数学模型，使用Isight软件结合ABAQUS有限元分析软件对锥形簧结构参数进行优化。

4.1 优化数学模型的建立

以影响弹簧结构强度的四个主要因素大圆弧半径R、凹槽深度h、型面倾角θ和小圆弧半径r作为设计变量，以弹簧刚度k作为约束条件，以橡胶部分的最大主应变范围ΔLE作为优化目标函数。建立优化数学模型如下：

min ΔLE=f(R，h，θ，r)
s.t. 0.616≤k≤0.784

R=[135，165]，h=[10，13]，θ=[45，60]，r=[3.5，5.5]

由于优化目标函数难以用明确的数学表达式描述，本文采用近似模型方法(Approximation Models)[18]来构造目标函数。近似模型是用来模拟一系列输入变量与输出响应之间的数学关系，主要用于难以用数学表达式描述的复杂工程问题。其基本思路是：采用DOE方法布置样本，并得到样本的响应函数值；然后根据样本及其响应值，采用拟合和插值方法构造近似模型；最后以近似模型为依据采用优化方法获取最优方案。近似模型可用下式来描述输入变量和输出响应之间的关系：

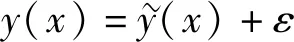
min ΔLE=f(R，h，θ，r)=y(x1,x2,x3,x4)=

响应面模型是近似模型中常用的一种模型，它是以试验设计为基础的用于处理多变量问题建模和分析的一种统计处理技术。构造响应面模型的最少样本点数依赖于模型阶数和输入变量个数。本文采用二阶响应面模型，初始化所需的最少样本点数为(M+1)(M+2)/2个。优化数学模型中有4个设计变量，故构造响应面模型最少需要15个样本点。

4.2 优化试验设计

为了获取构建优化数学模型的试验样本、提高模型的精确性，选用合理的试验设计方法进行试验设计至关重要。最优拉丁超立方设计方法是拉丁超立方设计方法的改进，它能够使所有的试验点尽量均匀分布在设计空间内，如图5所示，具有非常好的空间填充性和均衡性，使因子和响应的拟合更加精确真实。本文使用Isight软件提供的DOE模块，采用最优拉丁超立方设计方法，根据设计变量个数和取值范围，设计了15组试验样本作为输入变量，以刚度和最大主应变范围为输出响应，结合有限元分析技术，得到各样本点响应的数值，见表7。

图5 最优拉丁超立方

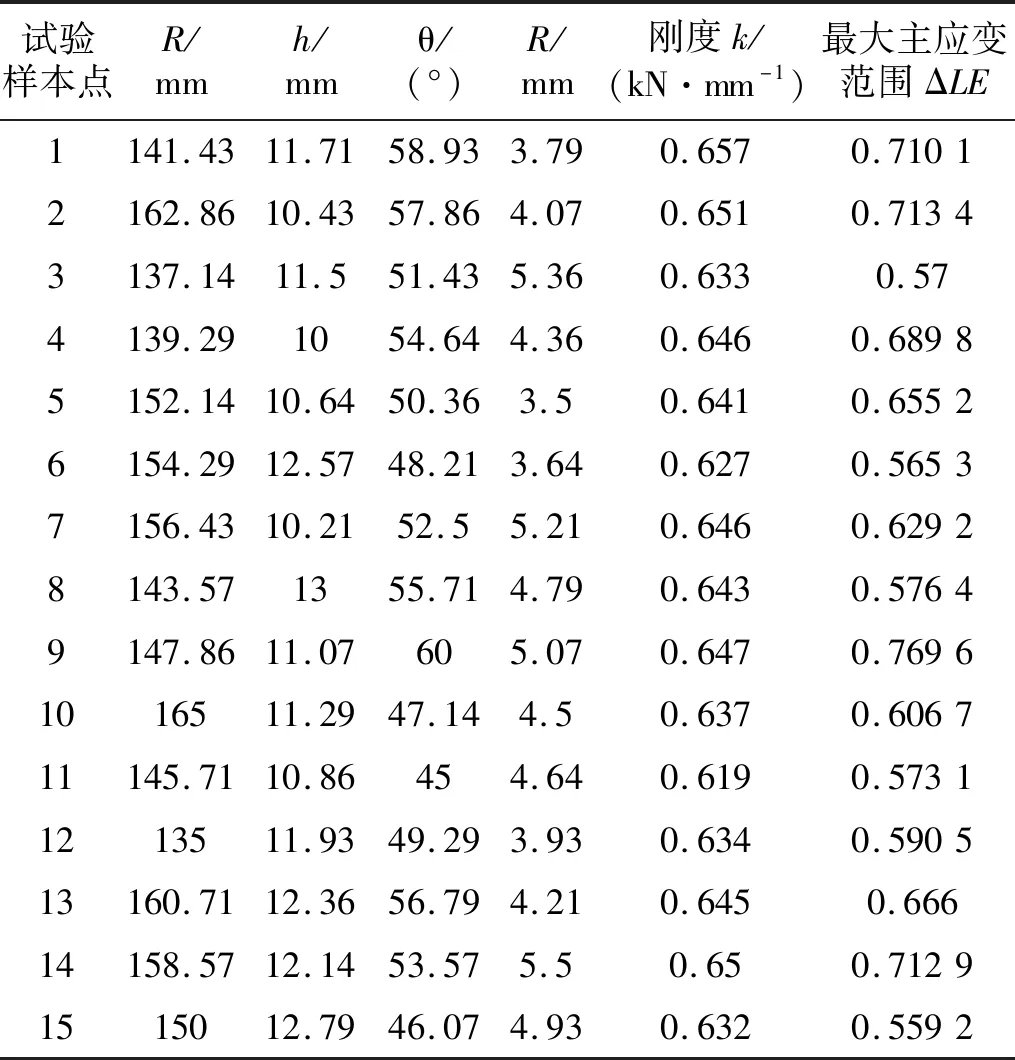
试验样本点R/mmh/mmθ/(°)R/mm刚度k/(kN·mm-1)最大主应变范围ΔLE1141.4311.7158.933.790.6570.71012162.8610.4357.864.070.6510.71343137.1411.551.435.360.6330.574139.291054.644.360.6460.68985152.1410.6450.363.50.6410.65526154.2912.5748.213.640.6270.56537156.4310.2152.55.210.6460.62928143.571355.714.790.6430.57649147.8611.07605.070.6470.76961016511.2947.144.50.6370.606711145.7110.86454.640.6190.57311213511.9349.293.930.6340.590513160.7112.3656.794.210.6450.66614158.5712.1453.575.50.650.71291515012.7946.074.930.6320.5592

4.3 结构参数优化

Isight软件的全域优化算法(Global Optimization)[18]适应性强：只评价设计点，不计算任何函数梯度；具有全局性：能求解全域最优解，避免了集中在局部区域的搜索。全域优化算法中的MIGA多岛遗传算法(Multi-Island Genetic Algorithm)具有比传统遗传算法更优良的全局求解能力和计算效率。

根据15组试验样本的输入变量和输出响应值，将其输入到Isight软件中，由Isight软件自动建立响应面模型，并选择多岛遗传算法作为优化算法，以弹簧刚度为约束条件、最大主应变范围为优化目标对锥形簧结构参数进行优化。通过优化，得到最优解的结果，如表8所示。

4.4 优化结果验证

根据表8中的最优解，圆整锥形簧结构参数为R=135 mm，h=13 mm，θ=50°，r=5 mm，然后设计锥形簧进行产品试验，并进行有限元仿真分析，产品试验和仿真分析结果分别与最优解进行对比，见表9。

表8 最优解结果Tab.8 Optimal result

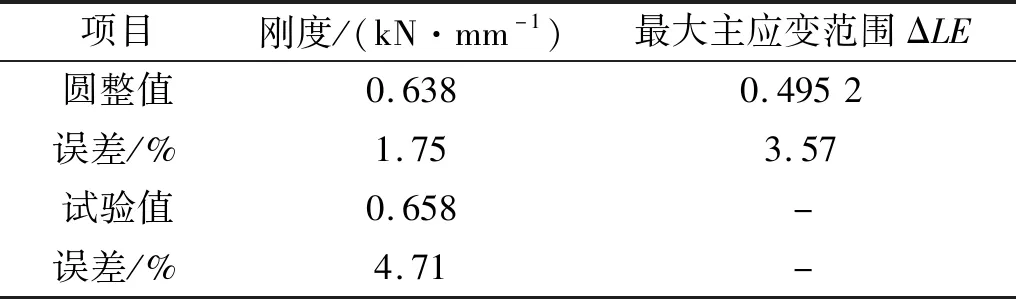
表9 锥形簧结构优化对比Tab.9 Comparison of structure optimization of conical spring

分析表9中的数据可知：根据优化结果对锥形簧结构参数圆整后进行仿真分析，仿真刚度值和最大主应变范围分别为0.638 kN/mm和0.495 2，与最优解的误差分别为1.75%和3.57%，与原结构相比，最大主应变范围降低了19.9%；锥形簧结构参数经圆整后的产品试验刚度值为0.658 kN/mm，与最优解的误差为4.71%，这可能是由于橡胶材料的非线性特性，导致试验值误差大于仿真值误差。

5 结 论

(1)采用Mooney-Rivlin橡胶超弹本构模型，对锥形橡胶弹簧进行有限元数值模拟，分析了橡胶弹簧的垂向刚度和最大主应变范围。

(2)基于正交试验方法，选取大圆弧半径R、凹槽深度h、型面倾角θ和小圆弧半径r为影响因素，进行锥形簧仿真试验，并对试验结果进行方差分析。分析结果表明：型面倾角θ对橡胶弹簧刚度和最大主应变范围影响最大，各因素对刚度的影响程度依次为θ>r>R=h，对最大主应变范围的影响程度依次为θ>h>r>R。

(3)基于二阶响应面模型和最优拉丁超立方设计方法，以大圆弧半径、凹槽深度、型面倾角和小圆弧半径为设计变量，以刚度为约束条件，以最大主应变范围为目标函数建立优化数学模型。采用MIGA多岛遗传算法对锥形橡胶弹簧结构参数进行优化，并将优化结果代入仿真模型进行试验验证，刚度和最大主应变范围试验结果与最优解结果的误差分别为1.75%、3.57%，优化结果精度较高，相比原结构最大主应变范围降低了19.9%；试验刚度值与最优解刚度值之间的误差为4.71%，满足刚度技术要求。