新型冲击响应谱发生器试验参数智能协同优化设计
2019-07-08刘承骛温晶晶
刘承骛, 温晶晶, 吴 斌, 陈 杰, 徐 丰
(西北工业大学 航天学院,西安 710072)
伴随现代飞行器高机动性与强稳定性的发展要求,力学环境试验成为飞行器运行前的必要考核阶段。冲击试验作为检验现代飞行器瞬态性能的力学环境试验之一,具有良好的实用性和可信性,主要分为经典冲击试验和冲击响应谱试验。经典冲击试验以实现单脉冲冲击波形为主(半正弦波,后峰锯齿波,梯形方波),目的是为考核飞行器的运载性能。垂直冲击试验机是进行经典冲击试验的主要设备,通过释放跌落台面,撞击波形发生器,产生单脉冲冲击波形。该设备具有结构简单,波形可调等优点[1]。图1为该冲击试验机的结构简图。

图1 垂直冲击试验机
单脉冲冲击波形单一且低频能量较高,因此提出冲击响应谱试验模拟复杂的冲击环境。冲击响应谱定义为一系列单自由度系统在复杂的振荡冲击信号激励下,其最大响应幅值随固有频率变化的包络谱线[2],该谱线表明试验对象在复杂冲击环境中的结构响应情况。
目前,国内外关于冲击响应谱试验方法的研究主要有:①火工品爆炸[3];②电动振动台;③机械撞击[4]。方法1利用火工品爆炸直接模拟真实冲击环境。由于火工爆炸的非线性与复杂性,目前关于火工冲击试验的研究较少[5]。方法2通过输入冲击时域波形控制电动振动台形成冲击响应谱,其核心技术为复杂冲击波形的时域合成方法。刘洪英等[6]利用衰减正弦波合成电动振动台时域控制波形。马道远等[7]结合遗传算法合成并优化冲击时域控制波形。基于电动振动台的冲击谱试验具有原理简单,效果良好等优点,但限于振动台的幅值与频率,该方法无法产生高幅值,宽频率的冲击响应谱[8]。方法3通过激励谐振响应装置产生复杂的振荡冲击波形,获得冲击响应谱,是当前应用最广的冲击谱试验方式。依据激励方式的不同,该类试验设备主要有摆锤式冲击试验机与气炮式冲击试验机。张华等利用ANSYS软件建立了摆锤式冲击试验机的参数化有限元模型,并提出了冲击响应谱的调试方法。Morais等[9]研究了摆锤锤头形状与冲击响应谱之间的内在联系。Parzianello等[10]基于气炮式冲击试验机,研究了响应信号采集位置对冲击谱的影响。
目前,针对机械撞击式的冲击响应谱试验,国内外的研究方向集中在冲击响应谱试验规律分析与指标调试方法等方面,缺少对试验设备设计与优化的研究工作。考虑到目前进行冲击谱试验需要开发专用的冲击谱试验机,成本较高且功能单一。因此,本文基于传统垂直冲击试验机,设计一种新型冲击响应谱发生器,在保留原垂直冲击试验机功能的基础上,对其进行扩充。随后利用Mindlin板理论推导简支矩形厚板的冲击响应表达式,分析简支厚板固有特性、激励载荷与冲击响应谱的关系。根据具体的冲击响应谱试验规范,结合有限元仿真与智能协同优化方案对冲击谱发生器进行优化,得到谐振板的最优尺寸与激励载荷。最后,通过仿真与试验对上述设计和优化结果进行验证。
1 新型冲击响应谱发生器设计
新型冲击响应谱发生器利用垂直冲击试验机的工作原理,在进行经典冲击试验的同时,实现冲击谱试验,扩展了传统冲击试验机的功能。
该冲击谱发生器的工作原理为:利用跌落台面首次撞击波形发生器后的反弹作为冲击激励载荷,作用于冲击响应谱发生器,使谐振板产生复杂的振荡冲击信号,从而得到冲击谱。为使反弹的跌落台面能够撞击冲击谱发生器的谐振板,需保证谐振板在竖直方向上的运动能力。通过导向杆和弹性软绳约束谐振板,使其只能沿竖直方向运动,同时安装阻尼缓冲器以防止谐振板与冲击谱发生器顶部的限位装置相撞。基于以上思路,设计的新型冲击响应谱发生器,如图2所示。
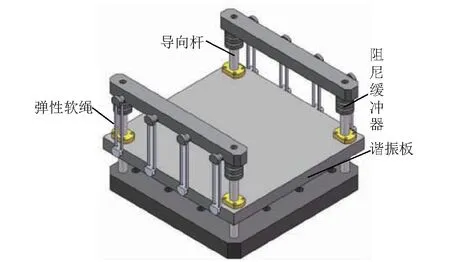
图2 冲击响应谱发生器
整个系统的工作过程如图3中(a)~(c)所示。冲击响应谱发生器安装于垂直冲击试验机的跌落台面上,当跌落台面自由释放时,冲击谱发生器会随台面自由跌落。当跌落台面撞击波形发生器反弹时,谐振板会因惯性作用,保持竖直向下的速度,并与跌落台面发生二次碰撞,产生振荡的冲击响应信号,形成冲击谱。
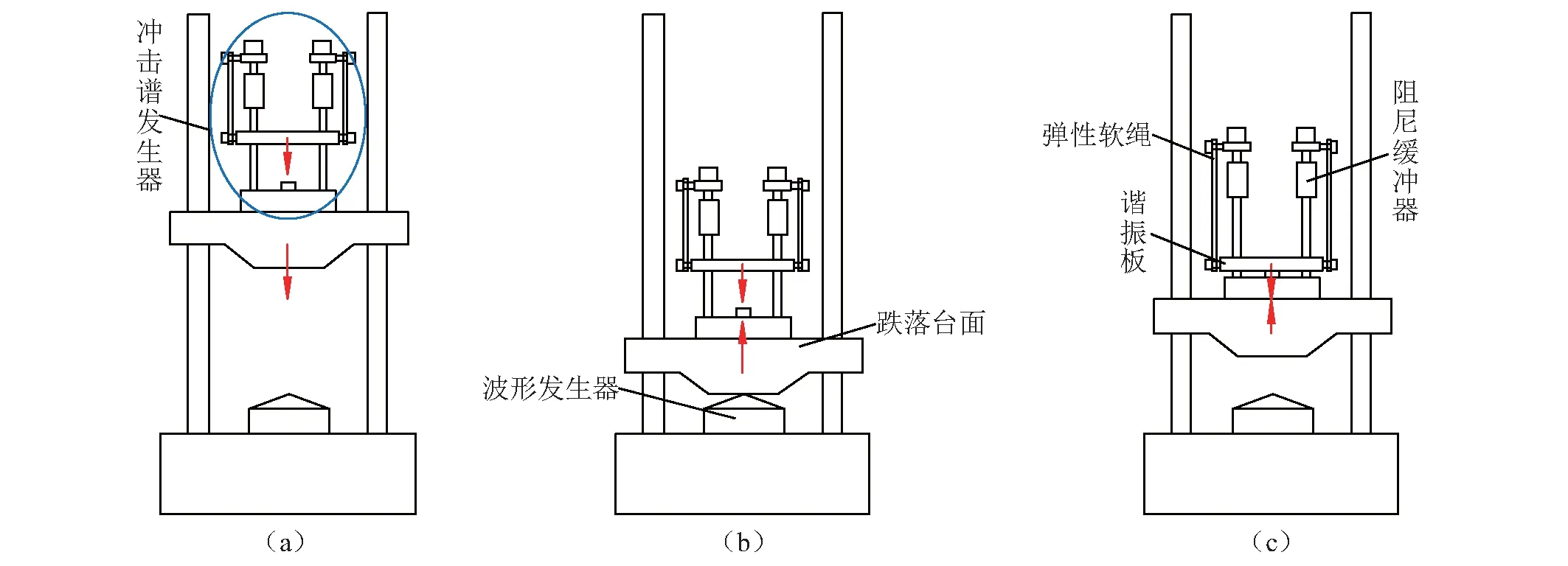
图3 冲击响应谱发生器工作原理
2 基于厚板理论的冲击谱分析
Mindlin板基于一阶剪切变形理论,考虑了厚板弯曲时,其中面的剪切变量,补偿了厚板的横向转动惯量,能够合理分析厚板的振动状态。简支边界具有解析振型,便于理论推导,本节采用四边简支的矩形厚板作为研究对象,分析冲击响应谱同厚板固有特性、激励载荷之间的内在联系。
2.1 矩形厚板响应分析
根据Mindlin板理论,矩形厚板自由振动的本征方程为
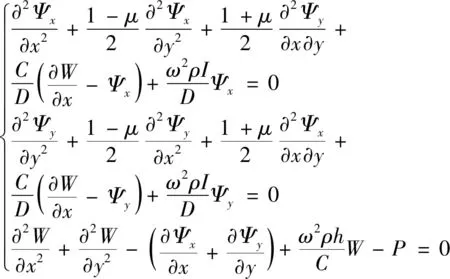
(1)
式中:W为横向位移;Ψx和Ψy分别为x和y方向的转角;ρ为厚板密度;μ为泊松比;h为板厚度;ρI为单位面积转动惯量;D=Eh3/12(1-μ2)和C=κ2Gh分别为厚板的弯曲刚度和剪切刚度,ω为固有圆频率,κ2=π2/12为剪切修正系数[11]。
化简式,可得厚板的横向自由振动微分方程为
(2)
对于四边简支的矩形厚板,各边仅可绕边线方向转动,且横向位移与转矩均为零,其横向振型函数为
(3)
式中:a和b分别为板长与板宽。参数m和n的组合顺序对应厚板固有振型阶数。
将式代入式可得厚板固有圆频率表达式
(4)
当谐振板与跌落台面发生碰撞时,通常会在碰撞位置安装一层橡胶垫作为激励垫块,其主要功能是缓冲碰撞与整形激励载荷。由于橡胶的超弹性与恢复性,矩形厚板的激励载荷F的形状可近似为半正弦[13],如图4所示。
设激励载荷具体表达式为
(5)
式(5)中,A为激励载荷峰值,D0为载荷脉宽。将激励载荷作用于矩形厚板底面形心处,其位置函数为
(6)
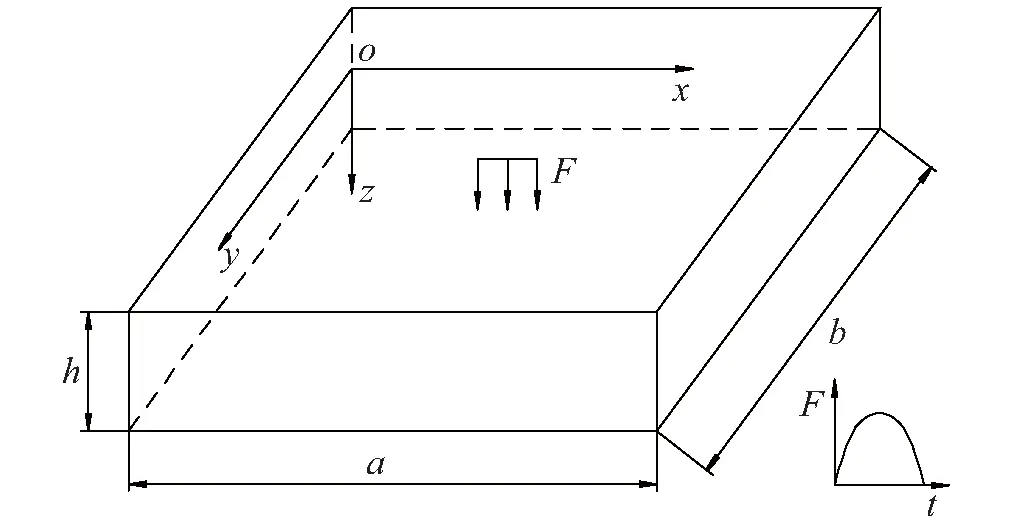
图4 谐振板激励载荷
结合模态叠加法与杜哈美积分[14],求解厚板在该激励载荷作用下,其上表面形心处的横向位移表达式
(7)
将式(7)对时间求导两次,得到加速度响应信号为
(8)
式中: 第一项为厚板在激励载荷作用时间内的强迫振动,第二项为激励结束后的自由振动,Dmn为厚板的各阶广义质量。
初步设计厚板的材料为硬铝合金,其材料参数和结构尺寸,如表1所示。

表1 厚板初始设计参数
为验证基于厚板理论推导的横向振动方程,本文选取Nastran软件进行仿真试验。
利用Mindlin板理论计算简支厚板在三组激励载荷作用下的响应信号,载荷参数,如表2所示。

表2 半正弦激励载荷
在Nastran软件中为矩形厚板剖分六面体网格。设置厚板的边界条件为四边简支,即边界上的节点不能横向移动,仅能绕边线方向转动。通过设置厚板任意相邻两条边为固定铰链约束(约束横向平动与纵向平动自由度),其对边为活动铰链约束(约束横向平动自由度),同时释放各边节点绕边线方向的转动自由度,以模拟四边简支条件,如图5所示。
运用软件中的瞬态响应分析模块求解矩形厚板在半正弦载荷激励下的响应信号。将理论与仿真计算结果进行对比,如图6~图8所示。

图5 四边简支矩形板
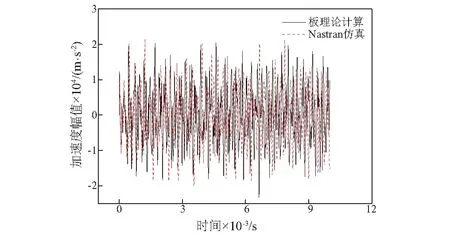
图6 第一组计算结果
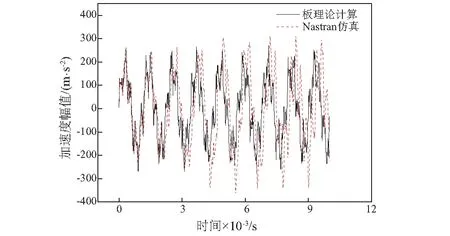
图7 第二组计算结果
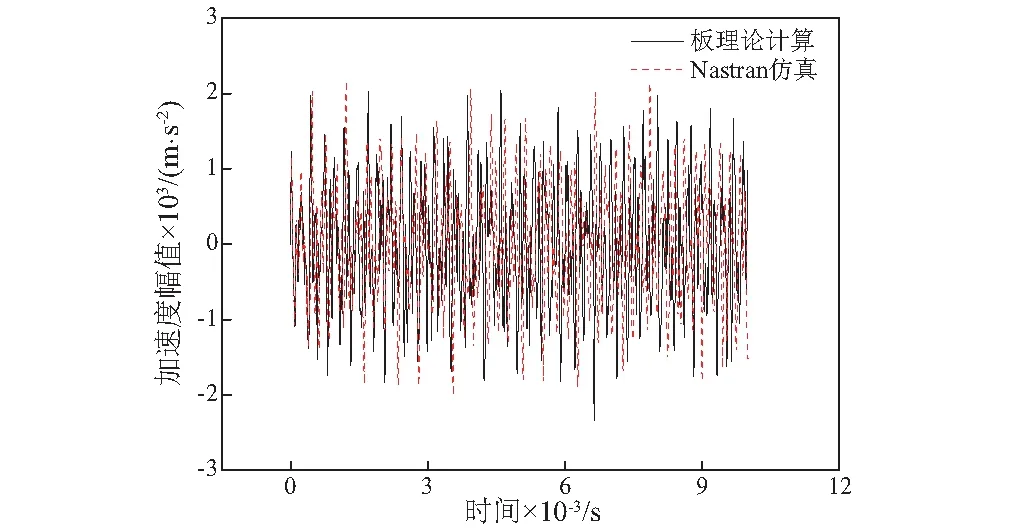
图8 第三组计算结果
对比三组计算结果可以发现,厚板理论计算结果与有限元仿真结果比较吻合。因此,基于Mindlin板理论计算谐振板的冲击响应是可行的。
2.2 冲击响应谱分析
为分析冲击响应谱同厚板固有特性、激励载荷之间的关系,利用公式和Nastran软件分别求解四边简支厚板的前五阶固有频率,结果如表3所示。

表3 厚板前五阶固有频率
可以发现,厚板理论与仿真计算结果基本相同。厚板前五阶振型如图9中(a)~(e)所示。
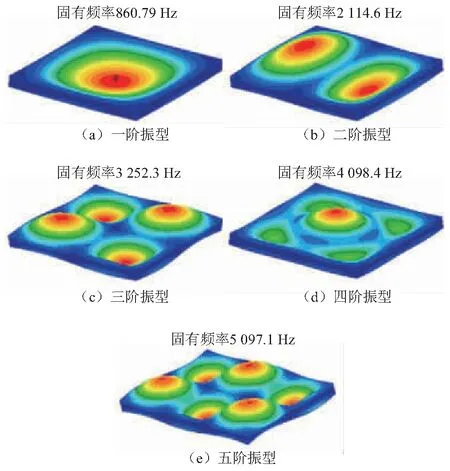
图9 厚板前五阶振型
将“2.1”小节中计算的三组厚板加速度响应信号转化为冲击响应谱,如图10~图12所示。
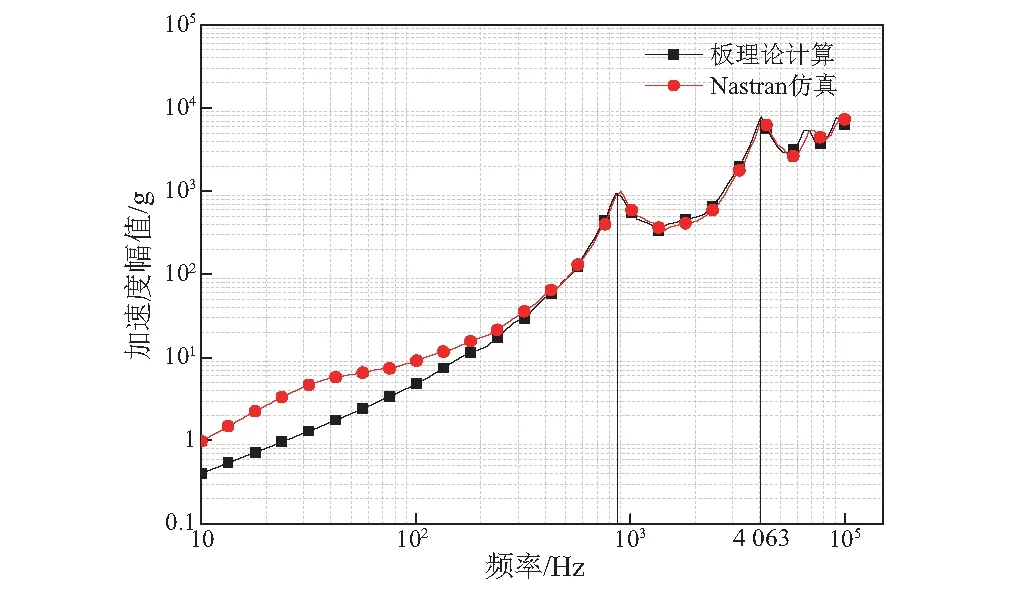
图10 第一组冲击谱
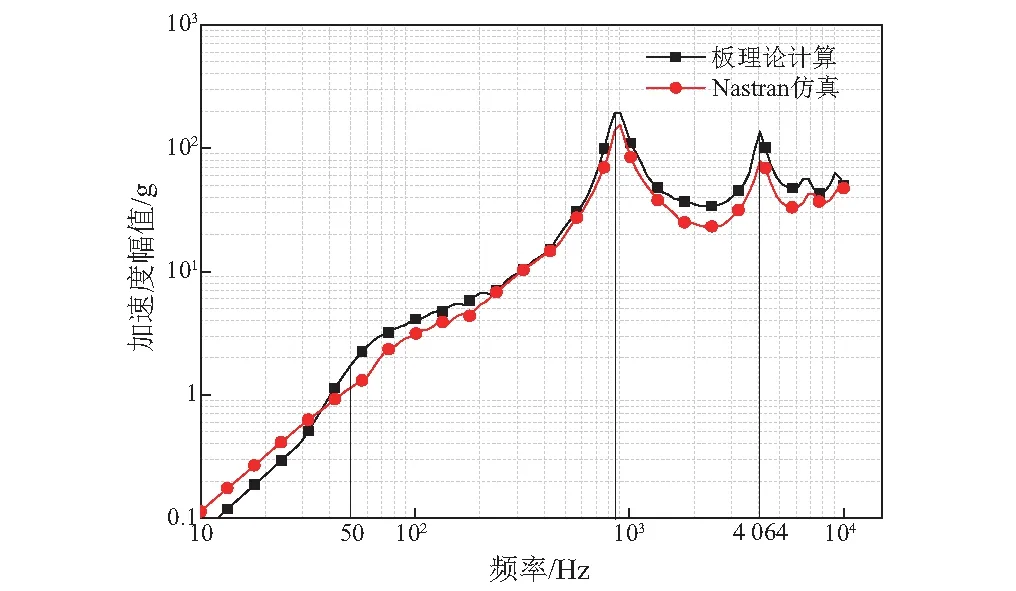
图11 第二组冲击谱
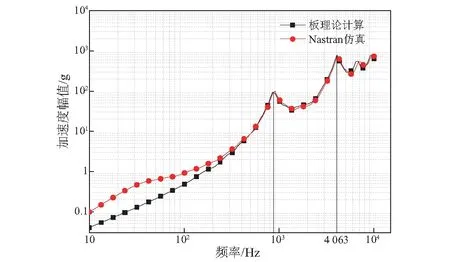
图12 第三组冲击谱
结合厚板振型图9可以发现,响应信号采集点位于厚板上表面形心处,厚板的一阶与四阶振型在该处的振动幅值最大,其余振型在形心位置不产生振幅。因此,三组冲击谱均在厚板第一阶与第四阶固有频率处存在峰值,即厚板的第一、四阶固有频率被激发。
由图10和图12可以发现,相同的激励载荷脉宽所形成的冲击谱线趋势基本相同,但激励载荷峰值越大,冲击谱整体幅值越大。
综上可知,决定冲击响应谱的主要因素为厚板固有特性与激励载荷,主要存在如下关系:
(1) 冲击谱在厚板部分固有频率处存在响应峰值,即厚板固有特性决定冲击谱峰值。
(2) 激励载荷幅值与冲击谱幅值的关系为正相关,载荷脉宽与冲击谱幅值为负相关。
3 智能协同优化方案设计
3.1 智能协同优化目的
冲击响应谱试验通常按照冲击试验规范条件设计。根据我国军用标准给出的冲击谱试验规范条件[15],如图13所示,冲击响应谱被分为低频上升段(f1~f2)和高频平直段(f2~f3)。 其中,k为上升段斜率,一般为+6 dB/oct,Amax为最大响应幅值,Φ为冲击谱容差带,通常为6 dB。
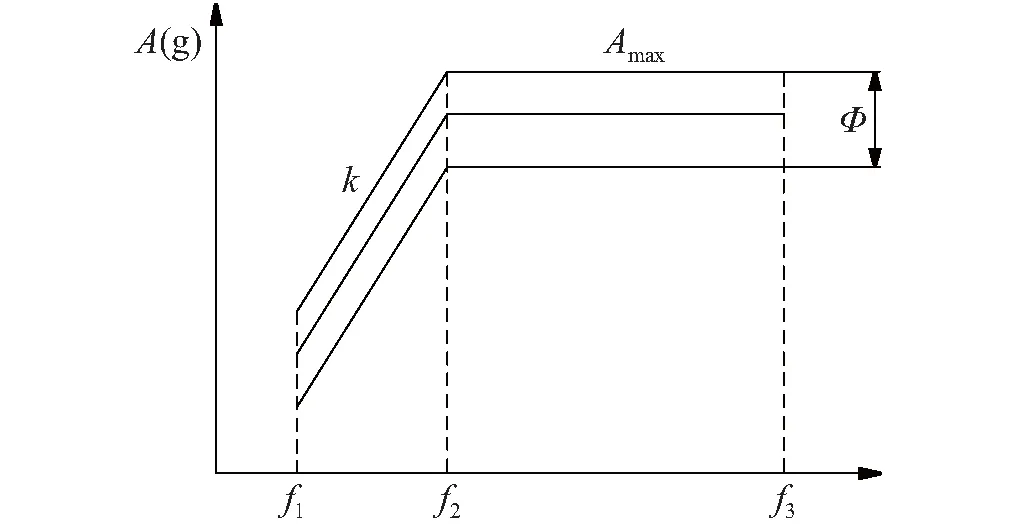
图13 冲击谱试验规范
本文以表4所示的冲击谱试验规范为目标,利用正交试验法构造仿真冲击谱样本数据库,通过支持向量机建立仿真冲击谱与目标冲击谱的均方根误差预测模型,结合多种群遗传算法寻求满足冲击试验规范的谐振板尺寸与激励载荷,优化冲击谱发生器。

表4 冲击谱试验规范
3.2 智能协同优化方案
正交试验是一种多因素试验设计方法,从全面试验样本中均匀整齐地选取最具代表性的部分试验样本,在保留试验样本完整性的同时,最大限度地减少了试验数量[16]。
支持向量机是一种基于统计学的机器学习方法,采用结构风险最小化准则,保证预测值与真实值的误差最小且置信度最大,具有较高的模型泛化能力。将具有全局代表性的正交试验样本作为该模型的学习样本,得到相对合理的预测模型[17]。
遗传算法仿照生物进化原则,在解空间中自适应搜索最优个体,其寻优模式为选择、交叉和变异。传统遗传算法通常存在局部收敛,进化不充分等问题。本文选择多种群遗传算法,建立具有不同搜索能力的种群,利用移民算子建立各个种群之间的联系,通过选择各个种群中的最优个体,实现全局寻优[18]。
结合正交试验、支持向量机和多种群遗传算法设计智能协同优化方案,寻求满足冲击谱试验规范的谐振板与激励载荷,该方案的流程如图14所示。
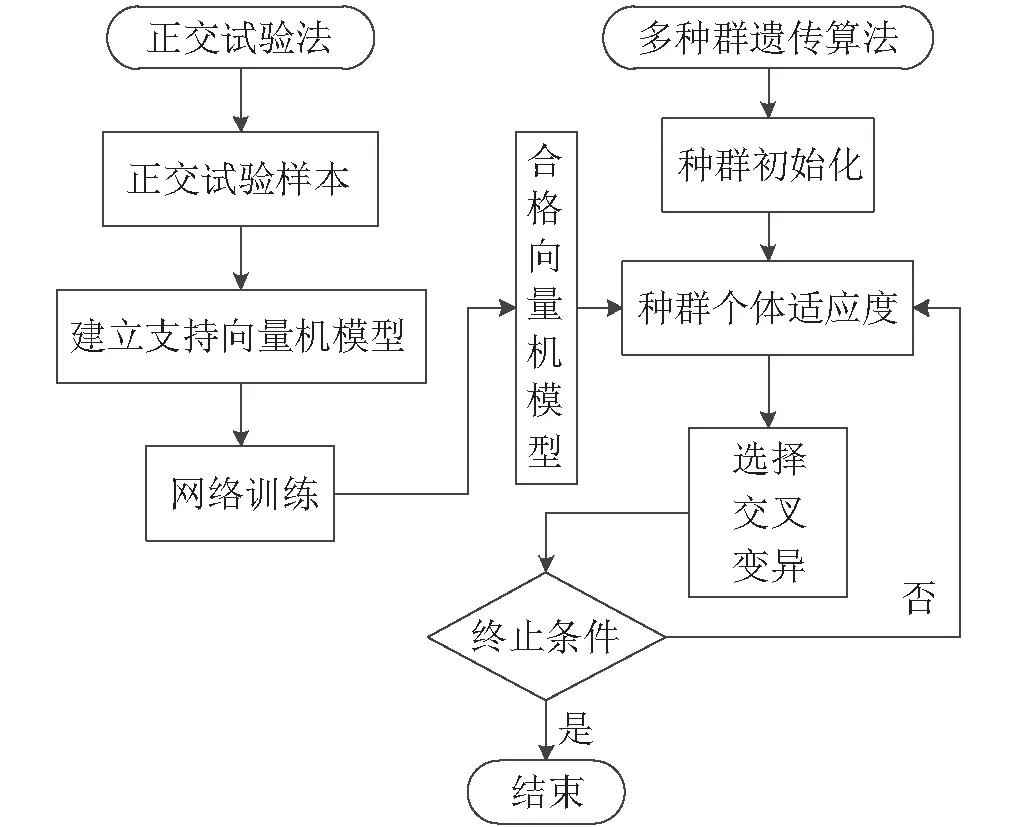
图14 智能协同优化方案流程
3.2.1 正交试验数据库
谐振板结构尺寸主要通过板长a、 板宽b以及板厚h确定,半正弦激励载荷可以通过峰值A和脉宽D0描述。因此,正交试验因素共五项。为保证谐振板具有足够的安装面积,设计试验因素水平范围如表5所示。
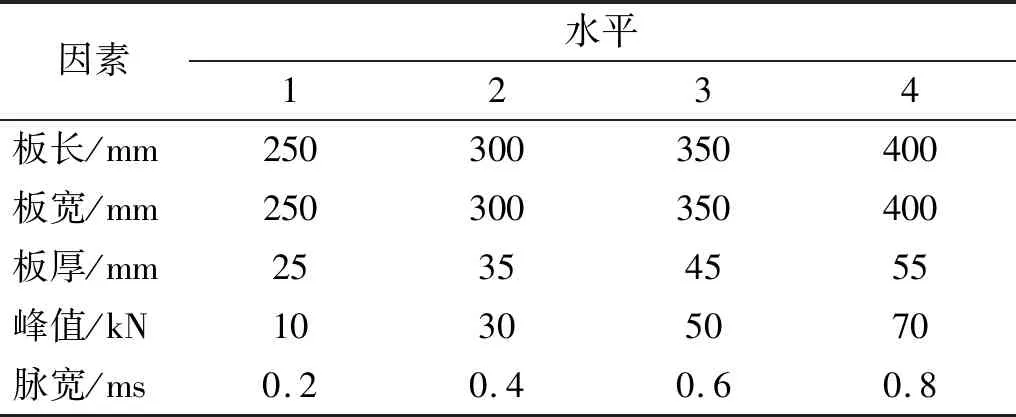
表5 正交试验水平分布表
基于5因素4水平的正交试验,采用的正交表为L16(45),即一共进行16组试验。考虑到试验样本数量较少,支持向量机建模数据不足,根据均匀选取的正交试验原则,本文将试验样本扩充到64组。
3.2.2 支持向量机模型
将正交试验所得的仿真冲击谱数据作为支持向量机预测模型的学习和检验样本,输入矩阵为谐振板尺寸与激励载荷
xT=(a,b,h,A,D0)
(9)
按照1/12倍频程,从起始频率10 Hz到终止频率10 000 Hz,选取仿真冲击谱上的121个点,计算仿真冲击谱与目标冲击谱的均方根误差,作为预测模型的输出。
选取高斯径向基核函数作为转换函数,如式(10)所示
(10)
式中:xi和x分别为输入学习样本和预测样本,σ2为核函数方差。
影响支持向量机模型预测精度的主要参数有目标函数惩罚因子c和核函数方差σ2。通过网格参数寻优法搜索最优的罚函数因子和核函数方差,建立最佳预测模型。
3.2.3 多种群遗传算法
在遗传算法中,个体之间的交叉概率和变异概率直接决定了算法的寻优能力。多种群遗传算法的优势在于其对多个种群设置了不同的交叉和变异概率,赋予各个种群不同的收敛能力,并建立了种群之间的联系,以实现最大范围内的寻优。
本文将支持向量机预测模型与多种群遗传算法结合。利用MATLAB进行支持向量机与多种群遗传算法编程,建立10个种群,每个种群中包含50个个体,其进化代沟均为90%。随机赋予各个种群一定范围内的交叉概率(0.7~0.9)和遗传变异概率(0.001~0.05),并设置最优个体最少保持代数为200代,作为算法的收敛条件。
4 智能协同优化结果
4.1 正交试验样本
利用Nastran软件,对64组正交试验输入样本进行仿真。考虑到冲击谱发生器上的谐振板通过导向杆约束。在Nastran软件中,通过释放谐振板导向孔内节点的横向自由度,约束其余自由度,以模拟导向杆的约束形式,如图15所示。

图15 导向杆约束
输入半正弦激励载荷进行瞬态响应分析,计算每组试验样本的冲击响应谱,如图16所示。
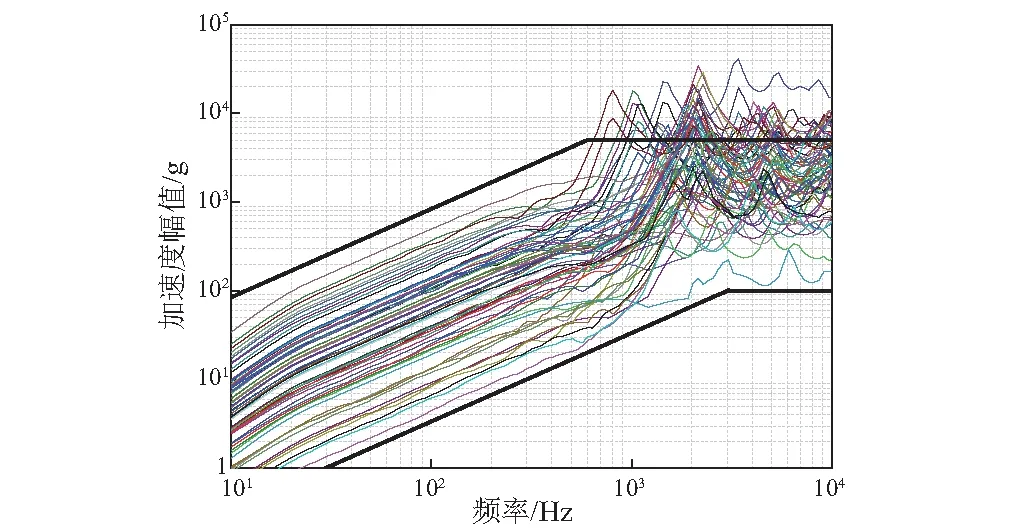
图16 正交试验仿真结果
从图中可以看出,64组冲击响应谱线斜率基本一致,为+6 dB/oct,幅值范围为100~5 000 g,拐点频率范围为600~3 000 Hz。由表4可知,目标冲击谱的试验规范条件在此范围内。
4.2 支持向量机模型建立
将谐振板尺寸与激励载荷作为支持向量机模型的输入,每组仿真冲击谱与目标冲击谱的均方根误差作为输出。随机选择56组试验数据作为预测模型的学习样本,其学习结果如图17所示。可以看出,该模型能准确预测出大部分真实的均方根误差。
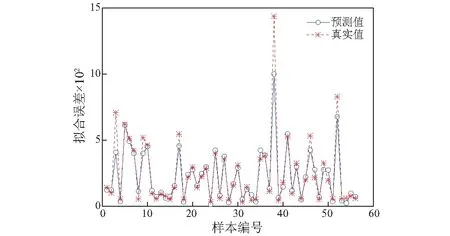
图17 支持向量机模型学习结果
为进一步验证该模型的预测能力,对8组未参与学习的样本进行预测,检验结果如图18所示。
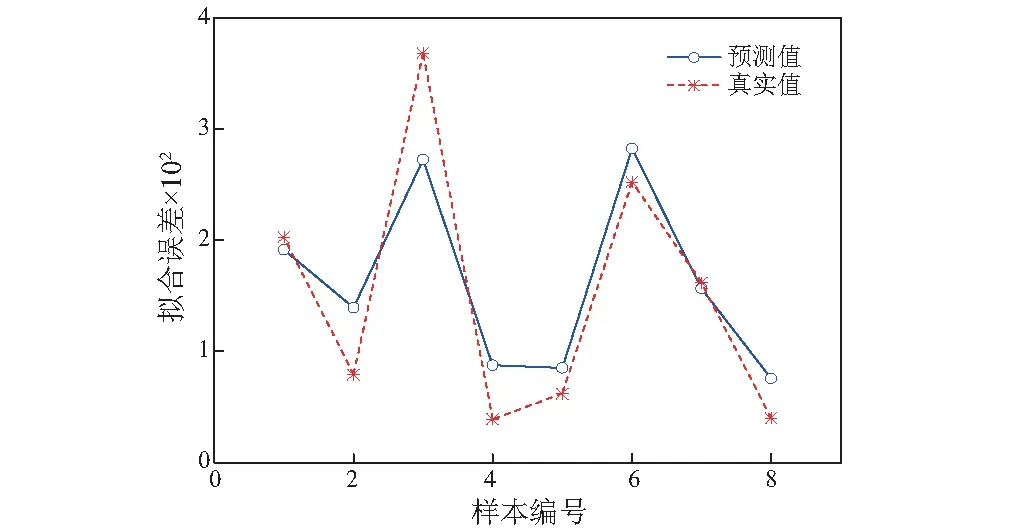
图18 支持向量机模型检验结果
可以发现,模型对未学习样本的预测结果比较准确,即该模型具有准确的预测能力。
4.3 多种群遗传算法优化
基于目标冲击响应谱的试验规范条件,利用多种群遗传算法进行5次全局寻优,收敛结果如图 19所示。可以看出5次收敛的函数值基本相同,平均值为27.7。
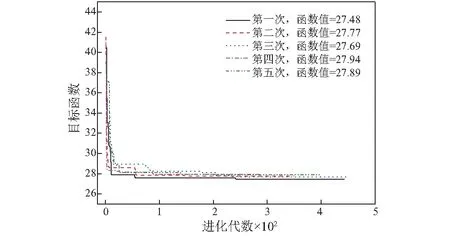
图19 进化收敛结果
寻优得到的谐振响应板尺寸与激励载荷,如表6所示。

表6 最优个体参数
5 试验验证
根据寻优结果,设计谐振响应板的最终尺寸为400×400×30,制造冲击响应谱发生器样机进行试验,如图20所示。

图20 冲击响应谱发生器样机
结合垂直冲击试验工作原理可知:跌落台面的跌落高度对应调节谐振板的激励载荷峰值,激励垫块的厚度对应调节载荷脉宽。经过反复调试,最终确定台面提升高度为200 mm,激励垫块厚度为10 mm。
对表6的优化结果进行仿真,同时利用样机进行试验,得到的加速度波形与冲击谱分别,如图21和图22所示。
由图21和图22可知,仿真波形与试验波形比较吻合,且其对应的冲击响应谱均满足表4的冲击试验规范。对比支持向量机模型的预测结果、仿真计算结果和试验结果,其均方根误差,如表7所示。
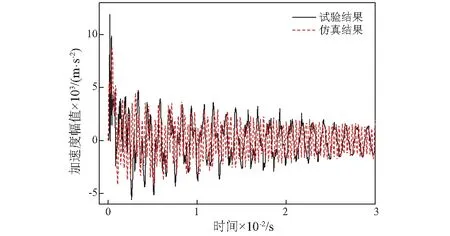
图21 加速度波形
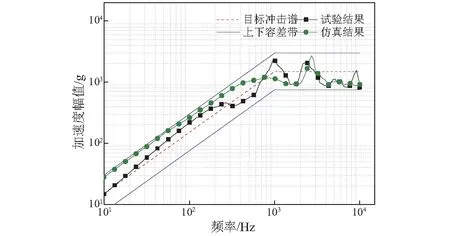
图22 冲击响应谱

冲击谱均方根误差优化算法预测仿真冲击谱试验冲击谱数值27.739.633.4
由表7可知,基于智能协同优化方案所预测的冲击谱均方根误差准确。
6 结 论
(1) 结合垂直冲击试验机的工作原理,设计了一种安装于垂直冲击试验机上的新型冲击响应谱发生器,扩充了传统冲击试验机的功能。
(2) 基于Mindlin板理论,推导并求解四边简支矩形厚板在半正弦载荷激励情况下的加速度响应表达式。分析了影响冲击响应谱的关键因素为厚板固有特性与激励载荷,得出了冲击谱峰值存在于厚板的固有频率处,且激励载荷峰值与冲击谱幅值呈正相关,脉宽大小与冲击谱幅值为负相关的结论。
(3) 基于冲击谱试验规范条件,设计智能协同优化方案,优化谐振响应板结构尺寸与激励载荷,得出最优设计为:谐振板长400 mm,宽400 mm,厚30 mm,载荷峰值为4.628 kN,脉宽0.8 ms。
(4) 根据优化结果进行仿真,并制造冲击响应谱发生器样机,调整跌落台面的跌落高度为200 mm、激励垫块厚度为10 mm,完成相应的激励载荷。试验结果表明:试验响应波形与仿真响应波形吻合,其冲击响应谱均满足冲击试验规范。
(5) 支持向量机模型预测的均方根误差为27.7,仿真结果误差为39.6,试验结果误差为33.4,验证了智能协同优化方案具有较强的可信度。
