基于RNR-WVD与GA-小波的非稳态排气噪声声品质研究

曾发林， 孙苏民

(1. 江苏大学 汽车工程研究院，江苏 镇江 212013；2. 江苏大学 汽车与交通工程学院，江苏 镇江 212013)

汽车的NVH研究已经从对噪声的控制发展到了噪声声品质研究设计的新阶段，传统以声压级为目标的车辆噪声研究已经满足不了当代消费者的需求。

汽车声品质反映了人对噪声的主观感受，目前关于声品质的研究多是采用主观评价试验，它能准确并直接反映出声品质，但耗时耗力。于是国内外学者提出了基于心里声学参量建立汽车声品质预测模型。Liu等[1]对支持向量机进行遗传算法优化，并建立了基于心里声学客观参量的柴油机声品质预测模型；申秀敏等[2]基于心里声学客观参量，建立了车内噪声声品质多元线性回归、神经网络和支持向量机3个预测模型，研究表明支持向量机模型预测精度更高；毕凤荣等[3]建立了基于心里声学客观参量、EEMD信号特征的最小二乘支持向量机模型研究了柴油机辐射噪声声品质。Lee等[4]提出基于小波变换的冲击声品质评价参数HFEC和粗糙度或是波动度共同作为多元线性回归模型的客观参数，用于悬架系统组件改进后的声品质预测。综上所述，关于汽车声品质的研究主要停留在探索阶段，声品质评价参数及模型建立没有统一标准。

车辆的排气噪声作为最主要的噪声源之一，研究其声品质对防制噪声污染大有裨益。本文首先在ArtermiS中基于Zwicker稳态与时变算法[5]分别得到稳态及非稳态信号的相关心里声学客观参量，并建立了基于心里声学参量的排气噪声声品质GA-BP预测模型。随后引入正则化非稳态回归计算WVD分布的方法，得到的系数矩阵建立具有衡量信号波动特性的参量SQP-RW与响度、尖锐度、A声级、峭度一起作为模型输入。同时引入GA-小波神经网络用于声品质预测。结果表明引入参量SQP-RW的GA-小波神经网络模型，在预测非稳态排气噪声中更加精确，可为非稳态排气声品质研究提供参考。

1 排气噪声主观评价模型

本文根据GB 1496—79《机动车辆噪声测量方法》,采用LMS测试并采集了10款国产车发动机转速分别为1 000 r/min、2 000 r/min、3 000 r/min、4 000 r/min、5 000 r/min下的稳态排气噪声信号，以及急加速、急减速非稳态噪声信号，记录发动机转速由1 000 r/min升至5 000 r/min及5 000 r/min减速至1 000 r/min的全过程信号。根据研究经验[6]，本文采用响度，尖锐度，粗糙度，波动度，峭度及A声压级作为初始建模的输入参量。样车1稳态噪声测试结果如图1所示，噪声的线性声压大体随着转速的升高而升高。

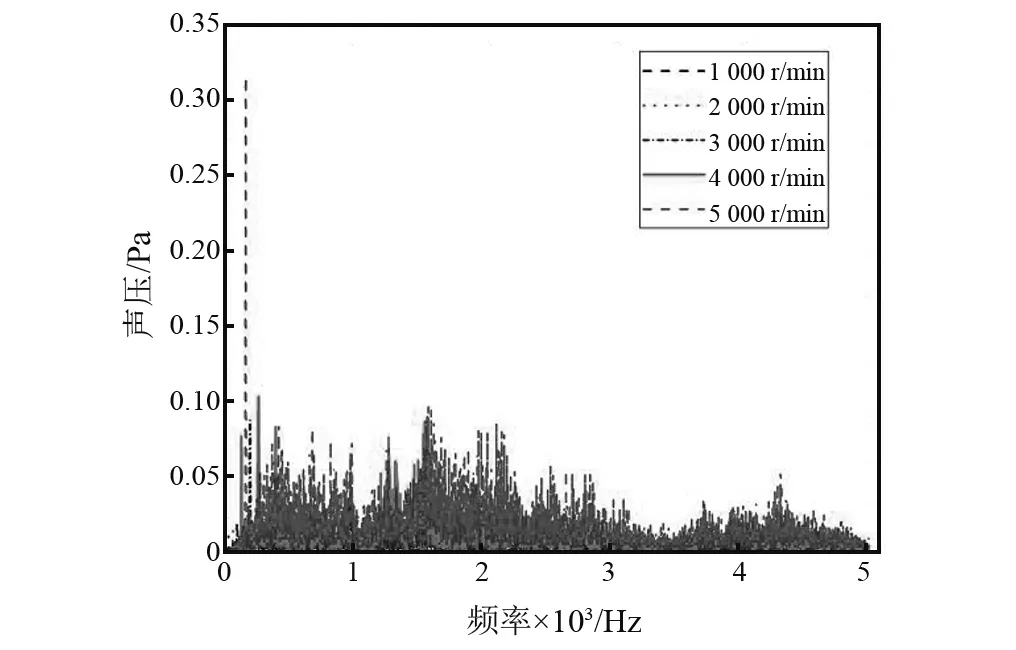
图1 样车1稳态工况排气信号

1.1 主观评价试验

本次主观试验样本虽较多，但考虑到评价人员的听音经验较少，为了试验更好的精度，采用成对比较法[7]进行，为了避免疲劳影响听音人员准确判断将试验周期变长。截取稳态工况信号5 s，截取具有非稳态工况特征信号15 s，将稳态信号样本作延时处理以消除时间长短的主观影响。样本两两配对比较，评价好的样本获得1分，差的不得分，若一组样本对听起来差不多，则都不计分。这样每个样本最终会得到一个确定的数值代表声品质的好坏，比较直观，为后期建模提供方便。

参与主观评价的人员共有42名，是来自某大学车辆相关专业的在读研究生及研究院的相关工作者。其中男性有24名，女性有18名，年龄基本在24～40岁之间。根据样本重合度和一致性系数[8]剔除了4名评价人员的数据后，最终得到样本的平均重合度为0.783，平均一致性系数为0.928。其中一致性系数采用Kendall法[9]计算，样本的心里声学客观参量及主观试验得到的统计结果如表1所示，满意度归一化公式见式(3)。

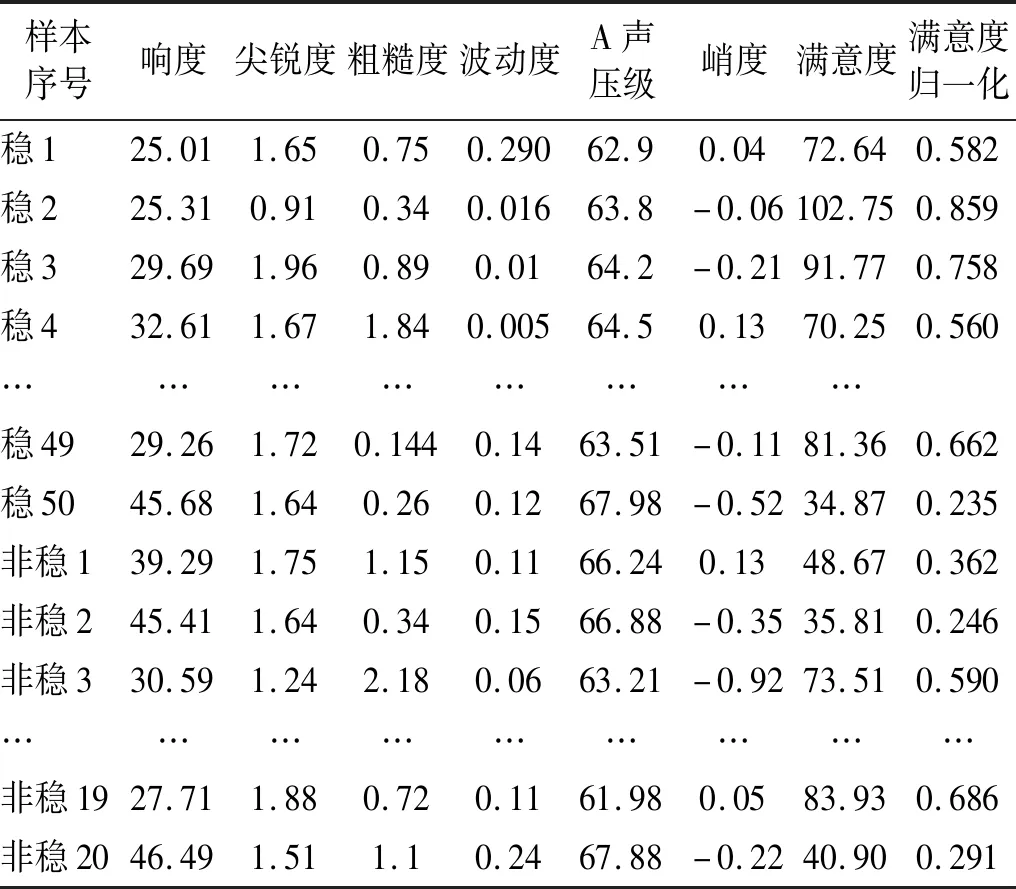
表1 样本心里声学客观参量值及满意度值

1.2 相关性分析

为了研究排气噪声主观满意度与心里声学客观参量之间的联系，采用SPSS.19软件对主观满意度和心里声学客观参量进行相关分析。稳态与非稳态分析结果如图2所示。因为样本含有非稳态噪声，其随着时间变化而会产生极端值，所以采用spearman秩相关双尾进行相关分析，spearman秩相关计算公式如下

(1)

式中：Ui和Vi是两变量的秩，作用是将定距型变量换成非定距型，减小极端值对结果的影响；n为样本数；r为spearman秩相关系数。

根据相关性分析，可以得出响度和尖锐度与满意度之间的相关性较大；除了粗糙度和峭度与主观满意度之间成正相关外，其他的参量与满意度之间成反比的关系。

注：**为双侧置信度为0.01时，相关性显著；*为双侧置信度为0.05时，相关性显著

2 稳态声品质预测模型的建立

采用BP(Back Propagation)网络建立稳态样本心里声学参量与主观满意度之间复杂的非线性映射关系，并采用GA(Genetic Algorithms)对神经网络的权值和阈值进行优化，不仅可以解决BP算法构建非线性模型易陷入局部极小值的问题，同时可以提高计算的效率及模型的准确度。所建立模型如图3所示。隐含层结点数n3根据式(2)计算后根据训练选取7结点。选取46个稳态样本作为模型的训练样本，剩下4个样本作为模型准确性的验证

(2)

式中：n1和n2分别为输入和输出层结点数，a为1～9的调节系数。

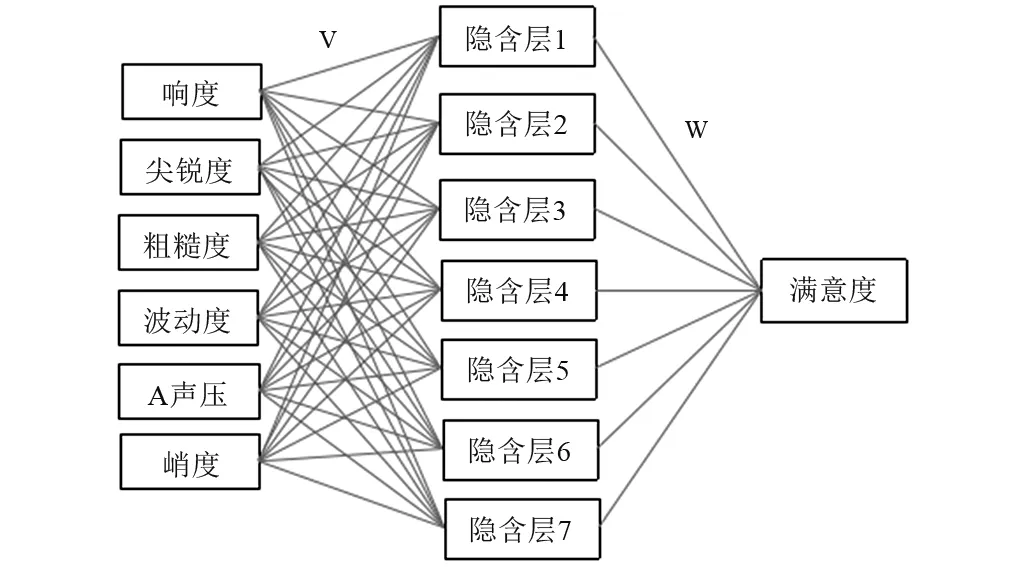
图3 所建GA-BP预测模型结构图

模型选用tansig作为隐含层的传递函数，purelin作为输出层的传递函数，网络学习算法选取梯度下降算法traingd， 学习效率ir取值为0.1， 动量系数mc选取为0.9； 以均方误差MSE作为网络训练目标函数，训练目标设置为0.001；遗传算法的最大遗传代数200，种群规模40，遗传代沟0.85，交叉概率0.7，变异概率0.01。训练前输入输出样本均作归一化处理，归一化公式如下所示

(3)

模型的训练结果如图4所示,4个验证样本预测误差分别为2.4%、1.8%、1.7%、3.4%，平均验证误差只有2.3%，证明所建立的GA-BP网络模型精度较高，满足稳态排气噪声声品质研究及预测的要求。

图4 GA-BP模型训练结果

3 非稳态排气噪声声品质模型建立

非稳态信号不同于稳态信号，其特征随着时间的变化会发生急剧的变化。根据图2的相关性分析结果，可以发现，对于稳态和非稳态排气噪声，响度、尖锐度与主观满意度之间的相关系数都比较大；峭度是度量信号分布经过标准化处理以后，相对于正态分布、高斯分布的尖峭或平坦程度的指标。稳态样本，峭度与满意度相关系数为0.159，非稳态样本峭度与满意度的相关性系数为0.127，相对于响度和尖锐度，峭度对于满意度的影响权重偏弱，但是稳态与非稳态系数相差不大，说明峭度在衡量非稳态噪声满意度中并没有发生比较大的误差，能够较精确的反映出信号的分布特性；粗糙度与波动度是反应人耳对调制音幅度与频率分布的感受程度，粗糙度在调制频率为70 Hz附近时效果最突出，波动度适用于20 Hz以下的低频调制信号并且在调制频率为4 Hz附近最明显。稳态粗糙度与满意度之间的相关性系数为0.271，波动度与满意度之间相关性系数为0.204，显著性水平均小于0.05；非稳态信号的粗糙度与满意度相关性系数为0.169，波动度与满意度相关性系数为0.103，与稳态噪声样本相比较，粗糙度和波动度相关性系数分别降低了37.6%和49.5%，这说明粗糙度与满意度没有精确体现出非稳态排气信号的波动变化特性。因此，为了更加准确的研究非稳态排气信号特征，引入时频分析能力较强的WVD分布，为了解决WVD分布自身存在的交叉噪声干扰，引入正则化非稳态回归(RNR)[10]技术计算WVD分布，得到声品质参数SQP-RW。同时，引入Morlet小波函数构造GA-小波神经网络对GA-BP神经网络进行优化，共同构建出声品质预测模型。

3.1 基于RNR-WVD信号分析

3.1.1 WVD分布及正则化理论

WVD是一种二次型分布，它能满足时频分析所期望的许多数学性质，并且它的变换形式比较简单，属于严格意义上的时频分析[11]。设有信号z(t)，它的Wigner-Ville分布定义为

(4)

式中：z(t)为对应的解析信号，在时间域，解析信号z(t)定义为

z(t)=x(t)+jH[x(t)]

(5)

式中：x(t)为实信号；t为时间；τ为延时；f为频率；z*为z的转置。H[x(t)]为实信号x(t)的Hilbert变换[12]。通过上述公式可以发现WVD分布中出现了乘积项，这会导致分析多频率信号时产生交叉干扰，影响信号的可读性。为了消除WVD分布带来的交叉干扰，引入正则化回归技术计算WVD，其核心是整形正则化理论，首先对整形正则化理论进行简单阐述：

正则化技术的目的是对估计的模型加强限制，以使不适定反问题得以求解。最常用的正则化方法是Tikhonov正则化[13]。Fomel[14]通过考虑整形算子的作用提出了整形正则化理论，该方法可以更加简单的选择正则化算子，例如高斯光化算子、带通滤波算子等。随后，Fomel又建立起整形正则化在非线性反问题中的理论基础。

用向量d表示数据，m表示模型参数，数据和模型之间的关系由正演算子L定义，表达式为

d=Lm

(6)

用最小二乘法计算，可以求解如下所示的优化问题

min‖d-Lm‖2

(7)

式中： ‖-‖2表示的是l2范数。最小二乘优法的目的是在已知数据d的条件下估计出最优解m。 而当算子L的条件数较大时， 直接反求解m是不稳定的， 考虑Tikhonov正则化方法， 对模型参数m加强约束，则有

(8)

式中：D是Tikhonov正则化项， 则式(8)的优化问题有下面的理论解

(9)

整形正则化理论考虑到了光化算子，一般意义下，光滑算子可以认为是约束模型在某个可被接受空间的映射， Fomel称其为整形(shaping)[15]。整形算子可以写为

s=(I+ε2DTD)-1

(10)

式中s为整形算子，又可推出

ε2DTD=s-1-I

(11)

将式(11)代入到式(9)，可以得到在整形正则化下形式上的理论解

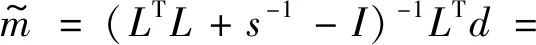
(12)

设离散的WVD分布为

(13)

其互相关函数R(n,m)定义为

(14)

式中：θ=min{n,N-n}， 可以推导出WVD的逆变换形式为

(15)

则式(15)的最小二乘最优解为

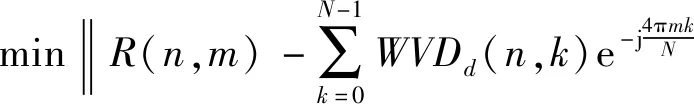
(16)

式(16)中的互相关函数R(n,m)和WVDd(n,k)分别是复数和实数，上述最优化问题在数学上是病态问题，因为求解的未知量比约束方程要多，此时引入上述的整形正则化算法便可以解决此问题。

人耳可听声音频率范围为20～20 000 Hz，采用巴氏高通滤波器对处理信号20 Hz以下频率进行滤波，并且进行基于Shannon准则的高频去噪，以消除无关信号的影响，图5为样车2加速信号处理前后对比频谱图。

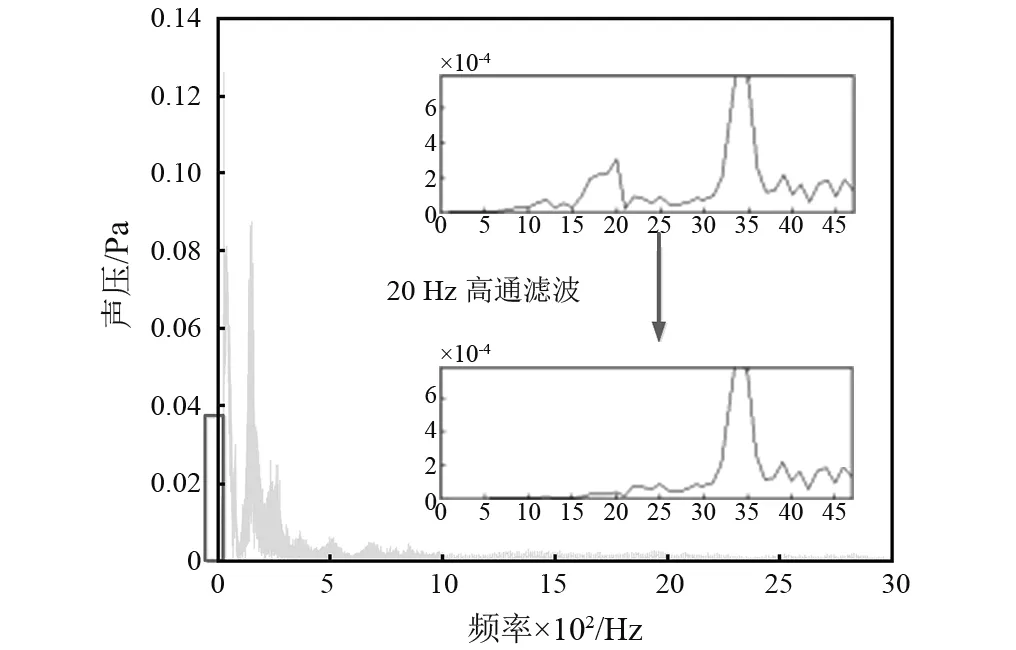
图5 滤波处理频谱图

本文采用大小可调整的高斯光滑算子作为整形算子。需要强调的是，利用RNR迭代WVD后计算得到的WVDd(n,k)是复数，因此将随时频变化的WVDd(n,k)的绝对值(模)定义为WVD时频分布。图6所示为WVD和经RNR优化计算WVD对样车2加速信号分析结果。由结果可以发现WVD分析出现了很多的“毛刺”，这主要是由于WVD分解本身算法引起的交叉噪声引起的，由对比的contour图可以清晰的观察到，通过引入光滑算子的RNR-WVD方法能有效的克服交叉噪声的干扰，并且使得信号具有更好的平滑性，时频分辨率也更加清晰，排除信号分析中一些虚假特征的干扰，会使信号特征的提取更加精确。

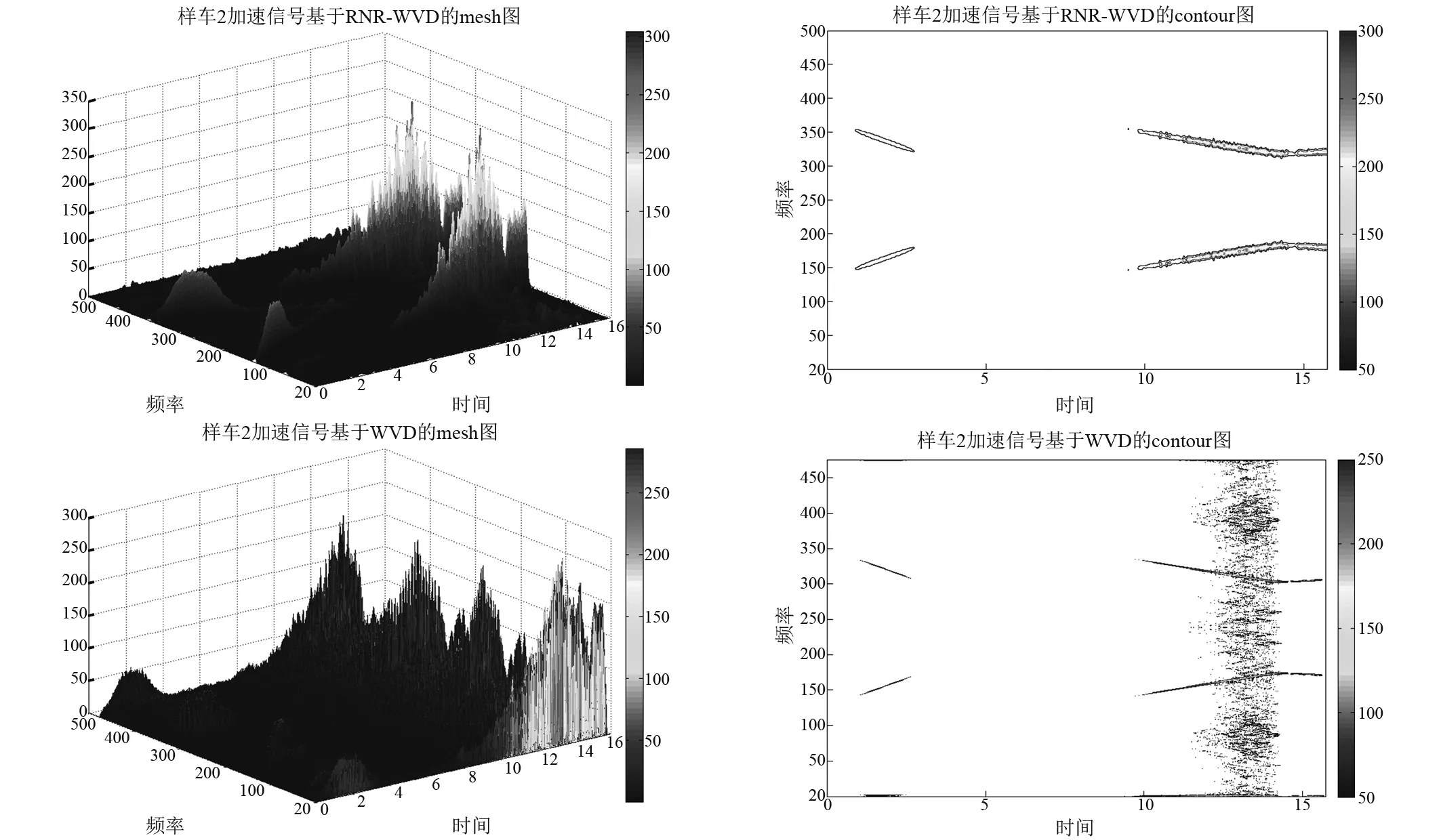
图6 样车2加速信号WVD和RNR-WVD分析结果

3.1.2 声品质参量SQP-RW的建立

基于上文的分析，经过RNR优化计算的WVD处理信号会得到关于信号时频信息的系数矩阵，系数矩阵包含了信号特征，由此，本文提出并建立了一个新的具有显示信号特征的声品质参量SQP-RW，SQP-RW的构建步骤如下：

步骤1信号前处理。对需要研究的非稳态排气噪声信号进行巴氏高通滤波及基于Shannon准则的高频去噪，消除无关噪声信号的干扰。

步骤2RNR-WVD变换。基于RNR-WVD变换对前处理后得到的非稳态排气噪声信号进行分析，得到k个m行n列的矩阵RWk,m,n, 其中k为研究信号个数20。

步骤4SQP-RW计算。计算基于RNR-WVD处理非稳态排气噪声得到的声品质参数SQP-RW

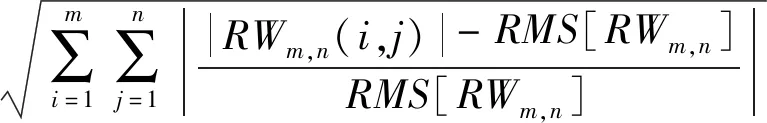
(17)

式中：k取1-20， RMS[-]求取系数矩阵有效值。

非稳态信号分布参数及规律随着时间不同会发生急剧变化，本文提出的SQP-RW参量能反映非稳态信号在时频域上的无序性、抖动性特征。经过RNR-WVD分布的信号会得到关于时间及频率分布的系数矩阵，以一维时间与一维频率为例，实际上系数矩阵是m行n列的，计算示意图如图7，系数曲线幅值偏离有效值越大，则计算参数越大，信号也就越陡峭；系数曲线越平缓，则计算参数值越小；同时在一定程度上可以度量信号距离有效值的分布特性。

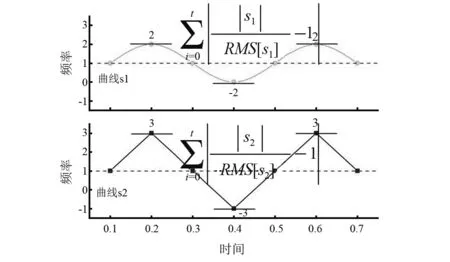
图7 SQP-RW值特性

经过相关性分析，结果表明在反映非稳态排气信号在调制频率下的特性中，粗糙度、波动度存在不足。由此，本文使用SQP-RW参量替换掉波动度与粗糙度，和响度，尖锐度，峭度，A声级共同作为GA-小波声品质预测模型的输入，10辆样车的输入参量，如表2所示。

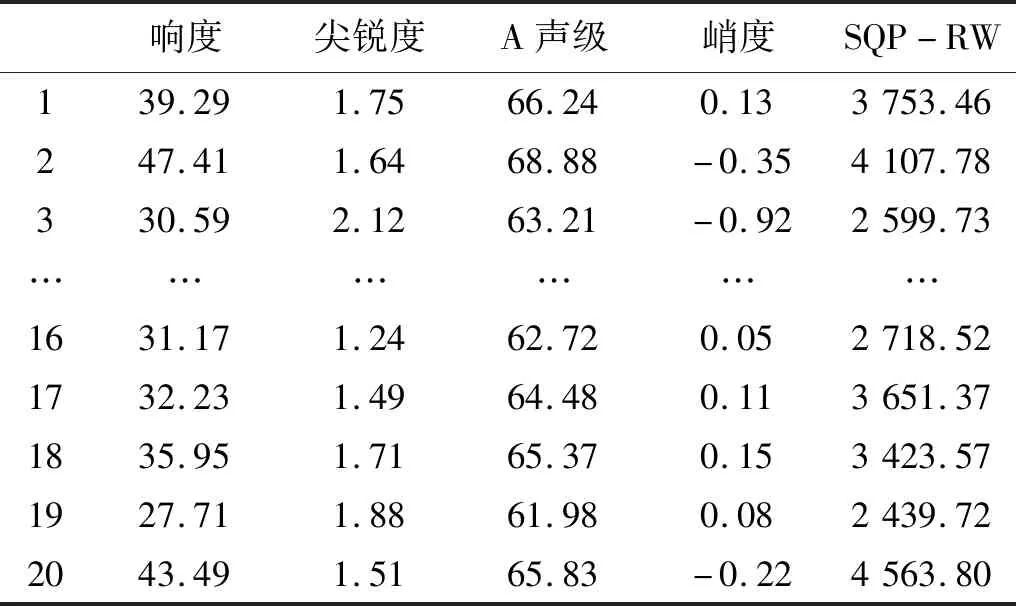
表2 新建模型输入参量值

3.2 GA-小波神经网络模型建立

3.2.1 小波神经网络

本文构建的小波神经网络是以BP神经网络拓扑结构为基础的，并以小波基函数[16]替代了BP网络中tansig函数作为隐含层结点传递函数的一种非线性神经网络。小波基函数具有正交性，紧支性等优点，可在一定程度上提高传统神经网络模型的抗噪性和泛化性。研究选用Morlet小波函数作为所建模型隐含层的传递函数，构造出的小波神经网络拓扑结构，如图8所示。

3.2.2 GA-小波神经网络模型

小波神经网络根植于BP神经网络，本质还是前馈型网络，与BP神经网络一样，层间权值和层内阈值随机初始化，易收敛于局部极小值、网络不稳定。因此采用GA优化小波神经网络的初始权值和阈值，遗传算法的设置参数与优化BP神经网络保持一致，如表3所示。

表3 遗传算法参数设置

所建的GA-小波神经网络模型的输入层有5结点，输出层为主观满意度1结点，根据公式2及训练最终确定了隐含层结点数仍为7。从而建立了一个5-7-1的GA-小波神经网络声品质预测模型。训练前SQP-RW参量值仍按照式3进行归一化处理。

3.3 非稳态排气信号声品质预测

将归一化后的非稳态排气噪声的响度、尖锐度、A声级、峭度和SQP-RW参量作为GA-小波神经网络声品质预测模型的输入，建立非稳态排气噪声声品质预测模型1；为了对比引入SQP-RW参量对于模型建立效果的影响，将响度、尖锐度、粗糙度、波动度、A声级和峭度作为GA-小波神经网络模型的输入进行训练，建立声品质预测模型2；同时为了检验GA-小波神经网络的性能，将非稳态噪声样本的响度、尖锐度、粗糙度、波动度、A声级和峭度作为GA-BP神经网络模型的输入进行训练，建立声品质预测模型3；以及非稳态排气噪声的响度、尖锐度、A声级、峭度和SQP-RW参量作为GA-BP神经网络训练输入建立声品质预测模型4，模型的相关信息统计，如表4所示。

表4 所建4种预测模型的信息

模型训练选取1～15号非稳态信号样本，16～20号样本作为模型训练后的测试数据。所建模型预测结果如图9所示，4个模型的预测精度分析，如表5所示。

由图9所示，GA-小波、GA-BP神经网络与所选定的输入参量均能较好的预测非稳态排气噪声声品质；根据表5，对于GA-小波神经网络而言，引入本文所建参量SQP-RW的模型1预测结果相关系数(R2)为0.978，均方根误差为4.22%，平均误差4.13%，都优于以传统心里声学参量训练的预测模型2；同时，对于GA-BP模型而言，引入本文参量SQP-RW训练的模型4的预测相关系数为0.966，均方根误差为6.14%，平均误差为6.08%，同样优于以传统心里声学参量训练的模型3；这表明，本文所建参量SQP-RW能够对非稳态噪声信号特征进行提取，适合作为预测模型的训练参数；考虑模型输入相同的情况，由分析结果可以发现基于GA-小波神经网络模型要比基于GA-BP神经网络模型精度要高；值得一提的是，虽然GA-小波相较于GA-BP在模型结构上得到了优化，但引入参量SQP-RW后训练的GA-BP模型4的预测均方根误差及平均误差要小于基于声学客观参量训练GA-小波神经网络的模型2，这表明对于特定的回归优化问题，其输入参量的优劣对于预测效果好坏影响权重很大。

图9 模型声品质预测结果

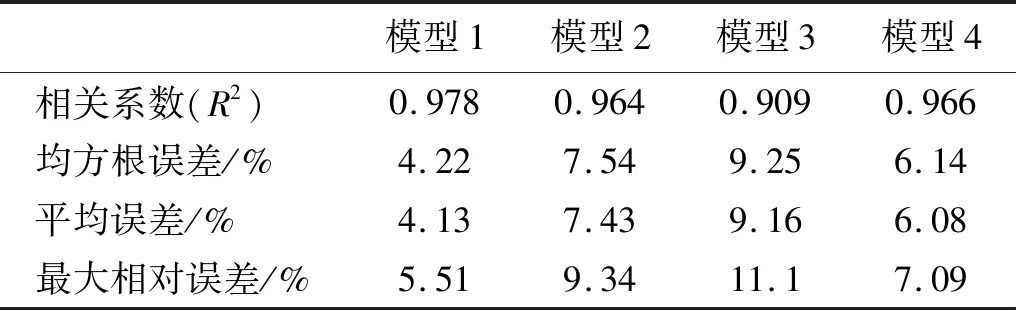
模型1模型2模型3模型4相关系数(R2)0.9780.9640.9090.966均方根误差/%4.227.549.256.14平均误差/%4.137.439.166.08最大相对误差/%5.519.3411.17.09

4 结 论

(1) 通过对排气噪声稳态与非稳态信号采集和主观评价，建立了稳态工况下的排气声品质GA-BP预测模型，所建模型预测精度较高，可用于稳态排气声品质的预测。

(2) 通过相关性分析，得到心里声学参量粗糙度和波动度与主观满意度相关性较低，并对稳态与非稳态工况相关性结果进行对比，得出对于非稳态排气噪声的研究，粗糙度与波动度在提取信号特征中存在不足。

(3) 引入WVD对非稳排气信号进行时频分析，并通过正则化回归技术优化计算WVD消除交叉噪声干扰，消除虚假信息；从而建立了具有非稳态信号波动特性的参量SQP-RW替换掉波动度与粗糙度作为模型的输入，同时引入GA-小波神经网络；为了对比所建预测模型的性能，也建立了非稳态信号的GA-BP模型。结果表明，引入参量SQP-RW建立的声品质模型精度更高，SQP-RW能体现出非稳态噪声特征；在输入相同的情况下，GA-小波神经网络较GA-BP能更准确的预测声品质。