对2018年全国I卷理科21题的研究*

四川省成都市大邑县师大三中 (611331)

李小强 邓文俊

四川内江师范学院数学与信息科学学院 (641100)

刘成龙

2018年数学全国Ⅰ卷理科21题是全卷的压轴题.试题考查了函数、不等式、导数等主干知识，蕴含丰富的数学背景，同时在解答方法上具有创新型和开放性，具有较强的选拔功能.因此，该试题是一道优秀的试题，值得我们研究.下文着重从命题背景、试题解法、试题变式对试题进行分析.

一、试题呈现

(Ⅰ)讨论f(x)的单调性；

二、命题背景

命题背景指命题时选取素材中含有的知识、模型、问题、文化、思想和方法等.(1)研究试题命题背景，有利于把握试题的本质、拓宽试题的解法、加强试题的变式．常见的试题命题背景有教材背景、现实背景、高考背景、竞赛背景、高等数学背景、数学文化背景等等.(2)21题含有丰富的背景，比如：高考背景、竞赛背景和高等数学背景.

背景一 高考背景

21题命题取材于高考真题：

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若f(x)有两个极值点x1,x2，记过A(x1,f(x1))，B(x2,f(x2))的直线的斜率为k.问：是否存在a，使得k=a-2？若存在，求出a的值；若不存在，请说明理由.

可以发现，21题和例1有惊人的相似度：构成f(x)的基本函数一致；第(Ⅰ)问问题一致；第(Ⅱ)问条件几乎一样；解答方法完全一致.因此，21题可以说是例1的翻版.

背景二 竞赛背景

21题含有对数—平均值不等式(ALG不等式)的背景：

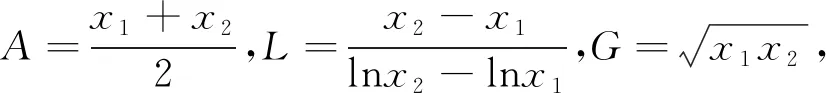
对数平均值不等式高于教材，但时常成为命题的热点素材，值得关注！

背景三 拉格朗日中值定理背景

图1

拉格朗日中值定理的几何意义是：在满足定理条件的曲线y=f(x)上至少存在一点P(x0,f(x0))，该曲线在点P处的切线平行于曲线两端点的连线AB.(如图1所示)

三、解法探究

下面给出21题第(Ⅱ)问的两种正确解法和两种错误的解法.

1.正确解法

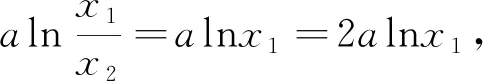
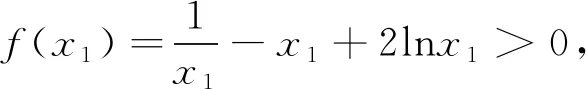
2.错解探究

图2

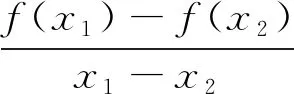
0(※)，只需证明g(x)=f(x)-(a-2)x为单调递减(*).(过程略)

评注:求导发现g(x)在定义域上既有增又有减，证明g(x)=f(x)-(a-2)x为单调递减不能实现.错误的原因是问题中的x1,x2不是任意的x，因此※与*不等价.

四、试题变式

变式是指相对于某种范式，不断变更问题情境或改变思维角度，使事物的非本质属性时隐时现，而事物的本质属性保持不变的变化方式.变式能有效扼制题海战术、能完善学生认知，帮助学生形成良好的认知结构.下面给出试题的变式：

(Ⅰ)讨论f(x)的单调性；

上述三个变式的解答读者自行给出.

文中从四个方面对21题作出了研究，权作抛砖引玉，希望读者继续探讨.