问题驱动 模型识别 揭示本质——基于求解初中几何最值问题的探究与思考

江苏省太仓市第一中学 (215400)

朱建良

建构主义理论提出，学生的数学知识是意义建构的，而不是被动灌输而成的．数学探究活动必须突出学生学习主体性，引导学生亲历体验并参与探究过程，通过学生自主探索和思考，在数学建模、类比转化等多方面得到进步和发展，从而提高探究活动的有效性．下面就初中几何最值问题的教学实践，谈谈如何通过建模教学，引导学生揭示几何最值问题的内涵，疏理方法，理解几何模型的深层意义，笔者意在抛砖引玉，以期广大同行指正．

1.解读问题，明确目标

1.1 疏理结构，探究特征

以苏科版义务教育《数学》九年级教材为学习内容，探究初三几何最值问题为主题，解读教材内容．在平面几何问题中，当某几何元素在给定条件变动时，求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题，称为几何最值问题．解决几何最值问题时应用几何性质有：(1)三角形的三边关系：两边之和大于第三边，两边之差小于第三边；(2)两点间线段最短；(3)连结直线外一点和直线上各点的所有线段中，垂线段最短；(4)定圆中的所有弦中，直径最长等．

几何最值问题是初中数学学习的一个难点，考查了学生的逻辑思维能力和空间观念，学生对此类问题往往感觉无从下手，找不到适当的切入点，导致思维阻滞，通过本课例的探究，尝试以数学建模为解决问题的突破口，基于问题解决，设计问题串展开探究学习，渗透“数形结合”、“类比”等数学思想，帮助学生揭示几何图形变换的规律、积累解决问题的策略，提升学生解决问题的能力．

1.2 理解问题，凝聚思想

求线段和的最值类问题的探究思路在于：通过平移、旋转及轴对称等图形变化转化为求两点之间或者点到直线之间的最短距离问题．此类问题的几何图形变换，往往改变了特殊点的位置，不改变形状和大小，可以通过建模，优化图形结构，整合图形信息，使复杂问题更直观、简洁．如遇涉及生活实际问题，可以通过对实际问题的分析、尝试，构建起相关几何模型，引导学生在质疑探究中感悟领略建模的思想和方法，提升学生的抽象、概括和演绎推理能力．

1.3 提炼模型，形成方法

基本模型1 在直线l上求一点P，使线段PA+PB最短．

如图1，作点A关于直线l的对称点A′，连接A′B交直线l于点P，∵PA=PA′，∴PA+PB=PA′+PB=A′B．此时，线段A′B最短．

图1 图2

基本模型2 如图2，当A、B两点位于直线l的异侧时，连接AB交直线l于点P，AP+BP=AB.此时，线段AB最短．

基本模型3 如图3，⊙O中过圆内一点P的最长弦是直线AB，当弦CD⊥AB于点P时，弦CD是过点P最短的弦．

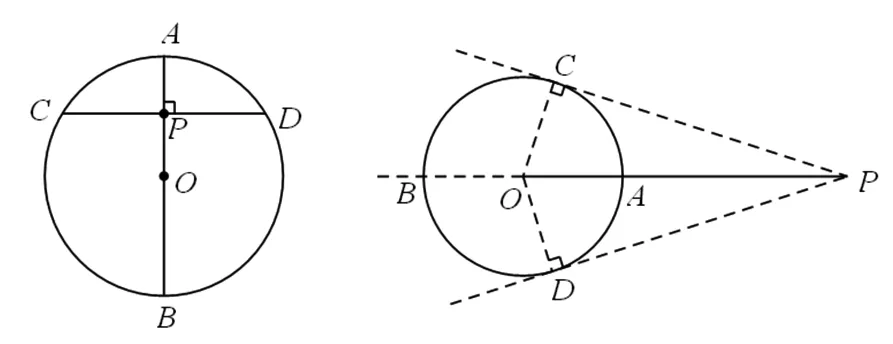
图3 图4

基本模型4 如图4，⊙O外一点P与⊙O上的点连接的线段中，PA最短，PB最长，当⊙O动点与点P的连线PO构成的角的度数最大时，有PC、PD与⊙O相切的位置．

2.凸现主体，回归模型

2.1 问题驱动，引领思维

数学模型描述了各变量间内的数量和位置关系，是指反映特定问题的数学关系结构，几何最值问题学习内容通过数学建模来表达和体现，把数学模型看做是几何知识的起点和主线．探究建模，不是简单地对数学公式、定义、定理、公理等逐条罗列，而是挖掘一组问题包含的数学模型，通过建模解决问题达到建构内化知识结构的目的．

图5 图6

2.2 合理设计，强化联系

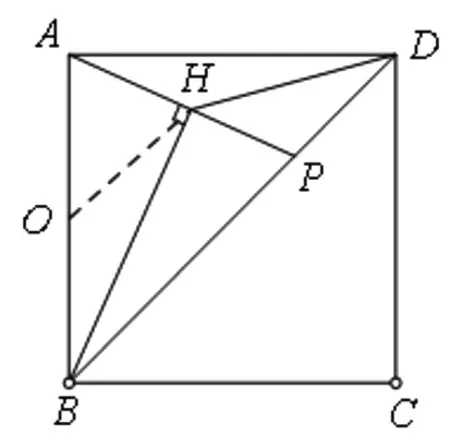
图7

拓展1 如图7，点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合)，连接AP，过点B作直线AP的垂线，垂足为H，连接DH，若正方形的边长为4，求线段DH长度的最小值．

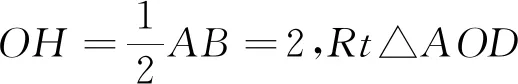
2.3 关注生成，优化策略

图8

拓展2 如图8，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点为A′，当CA′的长度最小时，求CQ长度．

3.追根溯源，积累经验

3.1 动态探究，寻求本质

数学建模的目的指向探究几何最值问题的本质，通过动态变换建模求解，引导学生获得一些关于几何最值知识或者建模技能和“基本经验”，在动态变化过程中寻求不变规律，在感性认识到理性认识的体验过程中积累基本的活动经验．

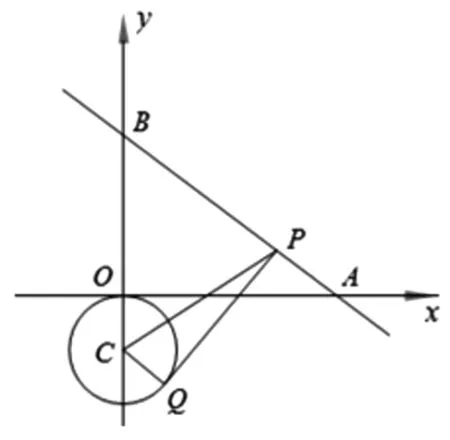
图9

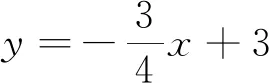
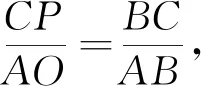
3.2 变式拓展，活化思维

变式1 如图10，在平面直角坐标系xOy中，分别以点A(2,3)，B(3,4)为圆心，以1,3为半径作⊙A，⊙B，点M，N分别是⊙A，⊙B上的动点，点P为x轴上的动点，求PM+PN最小值．

图10 图11

3.3 变式感悟，发展能力

变式2 如图12，已知A、B两点的坐标分别为(2,0),(0,2)，⊙C的圆心坐标为(-1,0)，半径为1，D是⊙C上的一个动点，线段DA与y轴将交于点E，求△ABE面积的最小值．

图12 图13

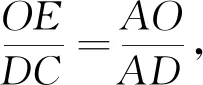
4.反思结构，优化方法

将几个背景相似、角度不同，但又在建模方法和解题技巧等方面具有相似性或有内在联系的几个最值问题组合在一起，作为一个几何最值问题系列展开探究，反思归纳，通过拓展问题，上升到思想方法的层面上去发展学生的思维能力．

拓展在直角坐标系中，已知点A(3,2),B(1,5)，(1)若点P坐标为(0,m)，问m为何值时，△PAB的周长最短，并求出△PAB的周长；(2)若点C、D的坐标分别为C(0,a)，D(0,a+4)，问a为何值时，四边形ABCD的周长最短，并求出此时的周长．

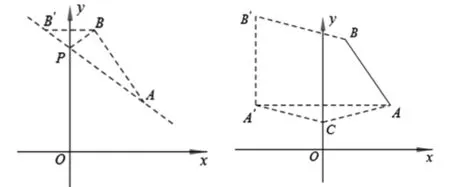
图14 图15

(2)如图15，作A点关于y轴的对称点A′，点A′(-3,2)，作A′B′∥y轴，取A′B′=CD=4，有B′(-3,6)，连接BB′交y轴于点D，∵A′B′∥CD，且A′B′=CD，有A′B′DC，直线BB′解析式为得此时四边形ABDC周长最短，为

5.解法自然，通性通法

设计问题对几何最值问题从不同角度、不同情形、不同层次做出有效变化，使几何最值问题的条件、结论及形式发生变化，以探究的变式问题为思维的载体，引导学生自觉体验几何模型的形成过程、逻辑推导过程和类比拓展提升过程．

变式如图16，在平面直角坐标系中，A(-4,0),B(0,4)，点C、D分别为OA、OB的中点，若正方形OCED绕点O顺时针旋转，得到正方形OC′E′D′，记旋转角为α(0<α<360°)，连接AC′，BD′，设直线AC′与BD′相交于点F，求点F的纵坐标的最大值．

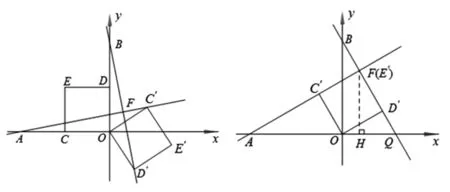
图16 图17

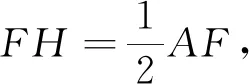
《数学课标(2011版)》中倡导“让学生获得广泛的数学活动经验”．学生数学学习的本质是学生自主建构自己对数学知识理解的过程，学生的学习过程是真正意义上的再创造过程．

探究几何最值问题，既要学会构图，循点觅形，生长图形，在动态变化中整体把握图形间的联系，提炼出基本模型，化繁为简，模型引领，揭示几何最值问题的本质属性．

求解几何最值问题是要顺着问题解决的脉络，引导学生从问题解决中建立几何模型解决问题，再从问题解决后自己产生新问题，再质疑，变式拓展，解一题，连一片，通一类，通过“螺旋递进式”的探究培养学生的问题意识，提升学生灵活解决问题的能力，进而体会探究数学问题的无穷乐趣，体悟成功的喜悦．