注入新元素 增添新感受
——寻求数学课堂新面貌
2019-07-08江苏省无锡市南湖中学214121
江苏省无锡市南湖中学 (214121)
郭淑娅
江苏省太湖高级中学 (214125)
何喜平
基于对提高学生的学习兴趣和增强数学教学的育人功能的思考,笔者一直在探索如何使数学课堂在提升学生核心素养的同时再带给学生一些美妙的感受,如带给学生一些心灵启迪,或者带给学生一些轻松与幽默等,使数学课堂变得轻松和谐,这能使学生对学习数学产生更多的积极情感与积极行为.经过一段时间的探索与实践,略有心得体会,在高三的一轮复习《函数与方程》中用三个成语“盲人摸象”“万象更新”“大象无形”引导课堂,给学生在知识的获取与能力的发展方面提供一些启迪,得到大多数学生的积极回应,现撰写成文与同行交流.
一、教学过程简介
1.盲人摸象
师:我们都听过“盲人摸象”的故事,这个成语常用来形容对事物只通过片面的了解就下结论的现象.但是,这个成语也有积极的一面.试想如果总结几位盲人的说法,或者让一位盲人多摸几处,大象的大概模样不也就清楚了吗?我们的学习过程也是如此,谁能一开始就掌握某一知识的全貌呢?试着回想一下你对某一知识的理解过程,一开始可能只是理解某一部分,然后又理解另一部分……直至你认识到这一知识点的全貌.这是知识从片面到全面,从局部到整体的发展过程.
问题:关于x的方程lnx+x-2=0在区间[1,2]上是否有解?为什么?
师:请大胆地说说你摸的“象”是什么?
生1:我想先求出这个方程的根,然后再看它的根是否在该区间内,但这个方程的根无法求出来.
师:虽然无法解出这道题,但你的方法也是有价值的,因为有一部分题目是可以这样做的.
生2:我的方法是令f(x)=lnx+x-2,可以判断出函数f(x)在定义域上是单调递增的,又因为f(1)=-1<0,f(2)=ln2>0,故函数f(x)在(1,2)内有唯一零点,即原题答案是有唯一解.
师:很好,你用的是什么方法?
生2:方程lnx+x-2=0的根即为函数f(x)=lnx+x-2的零点,可用“函数零点的存在性定理”来判断.
师:说得很好,你能说说“函数零点的存在性定理”的内容吗?
生2:若函数y=f(x)在区间[a,b]上的图像是一条不间断的曲线,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内有零点.
师:很好!还有其他的方法吗?
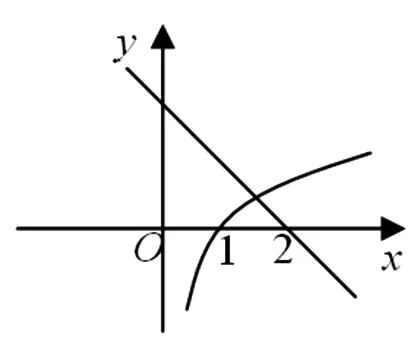
图1
生3:将原方程转化为lnx=-x+2,令f(x)=lnx,g(x)=-x+2,作出这两个函数的图像(如图1),因为原方程的根就是这两个函数图像交点的横坐标,故由图可知,原方程在区间[1,2]内有唯一零点.
师:很好!综合刚才三位同学摸的“像”,你能说说对于“方程根的个数问题”有哪些方法可以解决吗?
生4:有三种解决方法,方法1是直接求出方程的根;方法2是由于方程f(x)=0的根即为函数f(x)的零点,故可结合函数的单调性与函数零点的存在性定理来解决;方法3是将方程化为f(x)=g(x)的形式,然后转化为函数y=f(x)与y=g(x)图像交点的个数问题来解决.
师:总结的很好!非常感谢刚才几位同学的回答,因为这使我们对“方程根的个数问题”的认识,由片面到全面、由局部到整体,希望大家牢记这三种常用方法.
2.万象更新
师:“万象更新”通常指事物或景象改换了样子,出现了一番新气象.我想说的是:第一,通过接下来例题的讲解,希望每一位同学都能进一步认识“方程根的个数问题”及其三种常用方法的应用,从而更新自己原有的知识与方法;第二,当我们内心有新的领悟时,外在的面貌往往会表现出一番新气象,你们所有同学就是我眼中的“万象”,让我们共同努力,在课堂中看到“万象更新”的景象.
例1 若关于x的方程ex-ax=0(a∈R)有两个根,则实数a的取值范围是.
师:请思考这道题该怎么解?

图2
生5:将原方程转化为ex=ax,然后作出f(x)=ex与g(x)=ax的图像(如图2),函数g(x)的图像可视为一条经过原点的直线,a表示其斜率,故先求出g(x)与f(x)相切时的斜率,设切点为(x0,ex0),则切线方程为y-ex0=ex0(x-x0),将原点(0,0)代入,得x0=1,故切线斜率为e,所以实数a的取值范围是(e,+∞).
师:很好!还有不同方法吗?
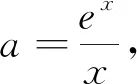
师:怎么行不通呢?将你的做法具体说一说.


图3
生7:不对,因为函数g(x)的定义域为{x|x≠0},故它的单调减区间应为(-∞,0),(0,1).它的图像应如图3,当x=1时,f(x)有极小值e,故实数a的取值范围是(e,+∞).
师:三位同学都说得很好,这两种做法都属于方法3.能用方法2做吗?
生8:令f(x)=ex-ax,则f′(x)=ex-a,若a≤0,则f′(x)>0,故函数f(x)在R上单调递增,不可能有两个零点;若a>0,令f′(x)=0,得x=lna,故当x∈(-∞,lna)时,f′(x)<0,f(x)单调递减;当x∈(lna,+∞)时,f′(x)>0,f(x)单调递增.当x=lna,函数f(x)有极小值f(lna)=a-alna,若a-alna≥0,即a∈(0,e],f(x)至多一个零点,不合题意;若a-alna<0,即a∈(e,+∞),因为f(0)=1>0,且当x→+∞时,f(x)→+∞,故函数f(x)在(-∞,lna),(lna,+∞)各有一个零点,即原方程有两个根.综上,实数a的取值范围是(e,+∞).
师:回答的很好,通过这道题,我们再次看到了如何用方法2与方法3来解决“方程根的个数问题”,接下来请大家思考例2.
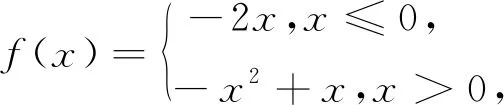
生9:我仍然是用方法3来尝试解这道题的,但是遇到麻烦了.
师:说说你进行到了哪一步?
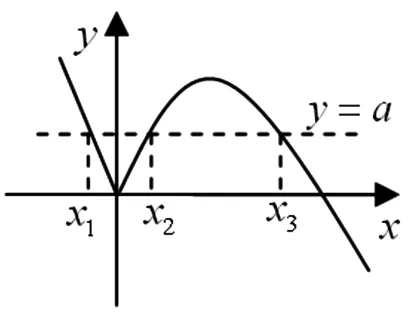
图4
生9:函数g(x)有三个不同的零点,即方程f(x)=a有三个不同的根,于是我将函数f(x)的图像作出来(如图4),设直线y=a与函数f(x)的图像交点横坐标从左到右依次为x1,x2,x3,但是接下来就不会做了.
师:很好!这里要求x1x2x3的范围,如何产生范围呢?
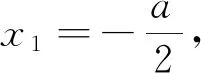
师:很好!看到刚才诸位同学活跃的表现,我感觉到在课堂中“万象更新”的场面.
3.大象无形
师:“大音希声,大象无形”出自《道德经》,是老子提出的一种美学观念,意为越好的音乐越寂静无声,越好的形象越飘渺无形,旨在推崇自然的、而非人为的美.借用“大象无形”这个成语,我想表达两个意思,第一是许多题目的内在本质是相同的,但外在形式却是多样的,面对多样的问题,我们要透过现象寻找本质;第二是“题无定法”,解题时不能拘泥于某一特定的方法,每一道题都有其不同的切入点,需要大家仔细审题.请大家做下面三道练习.
练习1 若函数f(x)=x2-ex-ax在R上存在单调递增区间,则实数a的取值范围是.
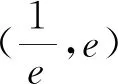

师:谁能说说第一题是怎么做的?
生10:函数f(x)=x2-ex-ax在R上存在单调递增区间,即f′(x)>0有解,因为f′(x)=2x-ex-a,故可化为不等式a<2x-ex有解,即a<(2x-ex)max.令g(x)=2x-ex,则g′(x)=2-ex,由g′(x)>0,得x 师:很好,此题本质上是不等式有解的问题,应当注意与“方程根的个数问题”间的区别.第二题该怎么解呢? 图5 师:此题本质上还是“方程根的个数问题”,你能从不同的角度考虑,很好!第二种解法也行,课后去将它完成,同学们之间也可以相互讨论.第三题该怎么做呢? 师:很好!第二小题怎么解呢? 生13:这道题的本质是不等式的恒成立问题,但我遇到困难了. 师:说说你的做法. 师:思路是正确的,可惜还差了一些,哪位同学可以补充一下呢? 师:回答的很好!在求函数的零点时,还可以用“设而不求”的方法,这与解析几何是密切联系的,说明数学各章节间的知识方法是相通的.请大家谈谈本节课的收获. 生15:本节课的收获是,一方面是认识了“方程根的个数问题”及其三种常用办法;另一方面从这三个“象”的成语感到自己对本课知识的领悟有一个动态的发展过程,先是对“方程根的个数问题”的认识从局部理解到整体把握,然后对这一问题及其解决方法的应用有了进一步的理解,最后的“大象无形”部分,我感觉到了一种境界,一种数学的美! 1.对本课教学环节设计的思考 数学学习的目标之一是提高学生的数学思维能力,包括:观察、实验、比较、猜想、分析、综合、抽象和概括.基于此,本堂课的教学过程分为三个环节,第一个环节是“盲人摸象”,通过学生对问题的解答,由学生总结并提炼出“方程根的个数问题”的求解方法;第二个环节是“万象更新”,在教师陪伴下,通过从多个角度剖析例题,使学生加深对这一问题的认识,并掌握其求解方法的应用;第三个环节是“大象无形”,在缺少教师帮助的情况下,当学生面对不同形式的问题时,培养其分析问题、解决问题的能力和优良的意志品质,从而提高学生的数学思维能力. 2.对数学课堂新貌设计的思考 教师在数学课堂上带给学生的,如果只是数字、符号、逻辑推理等,这会使课堂氛围显得单调、沉闷、缺乏活力,教学达不到理想的效果.本课用三个成语“盲人摸象”“万象更新”“大象无形”组成三个教学环节,让学生清晰地感受到课堂的教学过程及其发展,同时也给数学课堂注入一些新的元素,使课堂具有故事性、趣味性和意境感,这能使学生提高学习兴趣,对数学学习产生更多的积极情感,在课上展现出新的精神面貌与新的活力,课后乐意细细品味课堂的教学内容,使数学课堂呈现出其应有的面貌. 3.对课堂育人功能设计的思考 从“盲人摸象”环节到“万象更新”环节,再到“大象无形”环节,经历这些过程可以让学生明白一些道理:“盲人摸象”,让学生理解对事物的认识,由片面到全面、由局部到整体是一个过程,应当注重培养勇于探索和与人合作的精神;“万象更新”,教导学生要及时更新自己的知识与方法,对事物的认识要追求全面与整体;“大象无形”,一方面是让学生感悟到遇到复杂的问题时,须透过现象看本质,要有分析问题和解决问题的能力,另一方面是让学生明白“题无定法”,要根据题目的特征寻找解决问题的切入点.用这三个成语既表达了从局部到整体,从简单到复杂,从现象到本质的认识发展过程,又体现了层层递进的能力境界.“大象无形”既可以引导学生追求能力发展的新境界,也可以让学生感受到数学的自然之美.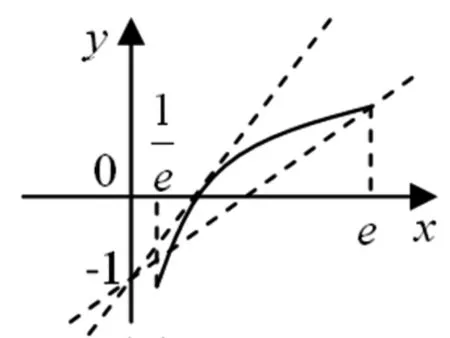
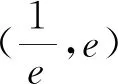

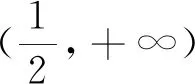
二、课后反思
