区间值映射的半连续性与凸性

李娜,包玉娥

(内蒙古民族大学数学学院,内蒙古 通辽 028043)

1 引言

区间值映射是取值为区间数的函数,是区间分析(区间数学)中的重要组成部分.为了建立区间值最优化理论[1-2]、区间值微分方程理论[3-4],人们开始讨论区间值映射的可微性及凸性等问题,并建立了相关理论.

最优化理论作为数学的一个重要分支,有着广泛的应用.然而在现实问题的建模过程中,由于一些数据或信息的不确定性,许多数学规划中用区间数表示数据或信息的变化范围[5-6].在讨论区间值规划的KKT最优性条件时区间值映射的凸性及相关性质起着关键作用[1,7-8].

文献 [9-10]讨论了区间值映射的极限及可微等问题,并给出了相关性质及其应用.本文在此基础上,进一步讨论区间值映射的半连续性及凸性问题.在第3节中,建立区间值映射的半连续性概念,并给出相关的性质.在第4节中,讨论半连续区间值映射的凸性问题.

2 预备知识

本节介绍区间数及区间值映射的一些相关概念.

设 R表示实数集,对任意R且,称有界闭区间为区间数,记为区间数全体构成的集合记为[R],并称 [R]为区间数空间.特别是,对a∈R,记为=[a,a],则∈[R].当0时,称为正区间数,其全体记为[R+],并称为正区间数空间.下面首先介绍区间数空间[R]上的加法运算、数乘运算及大小关系[8,11].

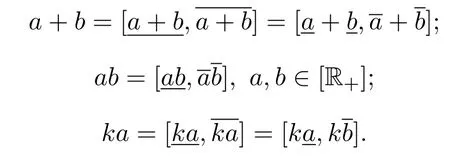
在上述序关系之下,易推出下面的结论.

引理 2.1设a,b,c,d∈[R],则

(1)a≤b⇔a+c≤b+c.

(2)a≤b⇒ka≤kb(k≥0).

(3)a≤b,c≤d⇒a+c≤b+d.

设M是n维欧式空间Rn的一个非空子集,映射F:M→[R]称为区间值映射,且记为

定义2.1[1,11]设M是n维欧式空间Rn的一个非空凸子集,映射F:M→[R]为区间值映射.若对任何α∈(0,1),有F(αx+(1−α)y)≤ αF(x)+(1−α)F(y),∀x,y∈M,则称F为M上的凸区间值映射.

引理 2.2[12]设M是n维欧式空间Rn的一个非空子集,若f是M上的实值函数且存在α ∈(0,1),使得f(αx+(1−α)y)≤ αf(x)+(1−α)f(y),∀x,y∈M,则数集

在[0,1]中稠密.

3 区间值映射的半连续性

本节主要引进区间值映射的半连续性概念及相关性质.为此,首先给出区间数空间子集的有界及确界的概念.

定义 3.1设A为区间数空间[R]中的非空子集.若存在区间数a∈[R],使得对任何x∈A,有x≤a,则称a为A的一个上界,且称A为有上界的子集.

设a0为A的一个上界,若对A的任何上界a,都有a0≤a,则称a0为A的上确界,记作a0=supA.同理可以定义A的下界和下确界b0=infA.

若A既有上界又有下界,则称A为有界集.

定理3.1若A为区间数空间[R]中的有界集,则A的上确界supA和下确界infA都存在,且supA=[supsup],infA=[infinf],其中.

证明设A为区间数空间[R]中的有界集,则存在,使得对任何x=[]∈A,有a≥x≥b,即且.所以由实数集的确界原理,有

下面证明a0=supA=[supsup],b0=infA=[infinf].

只需证明a0=supA=[supsup]即可,b0=infA=[infinf]的证明类似.

假设a0supA,那么存在A的一个上界a1=[11]∈[R],使得a0>a1.从而01且01.又因为对任何x∈A,有x≤a1,即1且1.所以

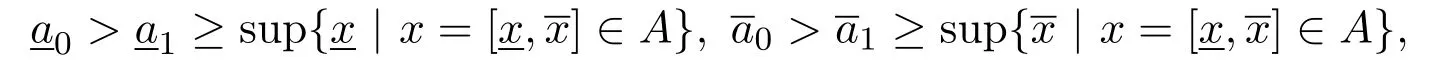
这与0及0的定义相矛盾,故a0=supA=[supsup].

定义 3.2设F:M→[R]是一个区间值映射,x0∈M.如果对任意ε>0,存在δ>0,对任何x∈M,当‖x−x0‖<δ时,有,则称F在点x0处下半连续.

如果F对M中的每一点都下半连续,则称F在M上下半连续.

定理 3.2设F:M→[R]是下半连续的区间值映射,则实值函数(x)和(x)在M上下半连续.

证明设F:M→[R]是下半连续的区间值映射,x0∈M,则对任意ε>0,存在δ>0,当x∈M且‖x−x0‖<δ时,有F(x0)≤F(x)+.所以

从而由实值函数的半连续性概念,有实值函数(x)和(x)在M上下半连续.

定义 3.3设F是区间值映射,若存在A=[]∈[R],当x∈M时,有F(x)≤A,则称F为有上界的区间值映射.如果存在B=[]∈[R],当x∈M时,有F(x)≥B,则称F为有下界的区间值映射.

定理 3.3设M为闭集,F:M→[R]为下(上)半连续区间值映射,则F为有下(上)界的区间值映射.

证明设F:M→[R]为闭集M上的下半连续区间值映射,x0∈M,则对任意ε0>0,存在δ0>0,当x∈M且‖x−x0‖<δ时,有

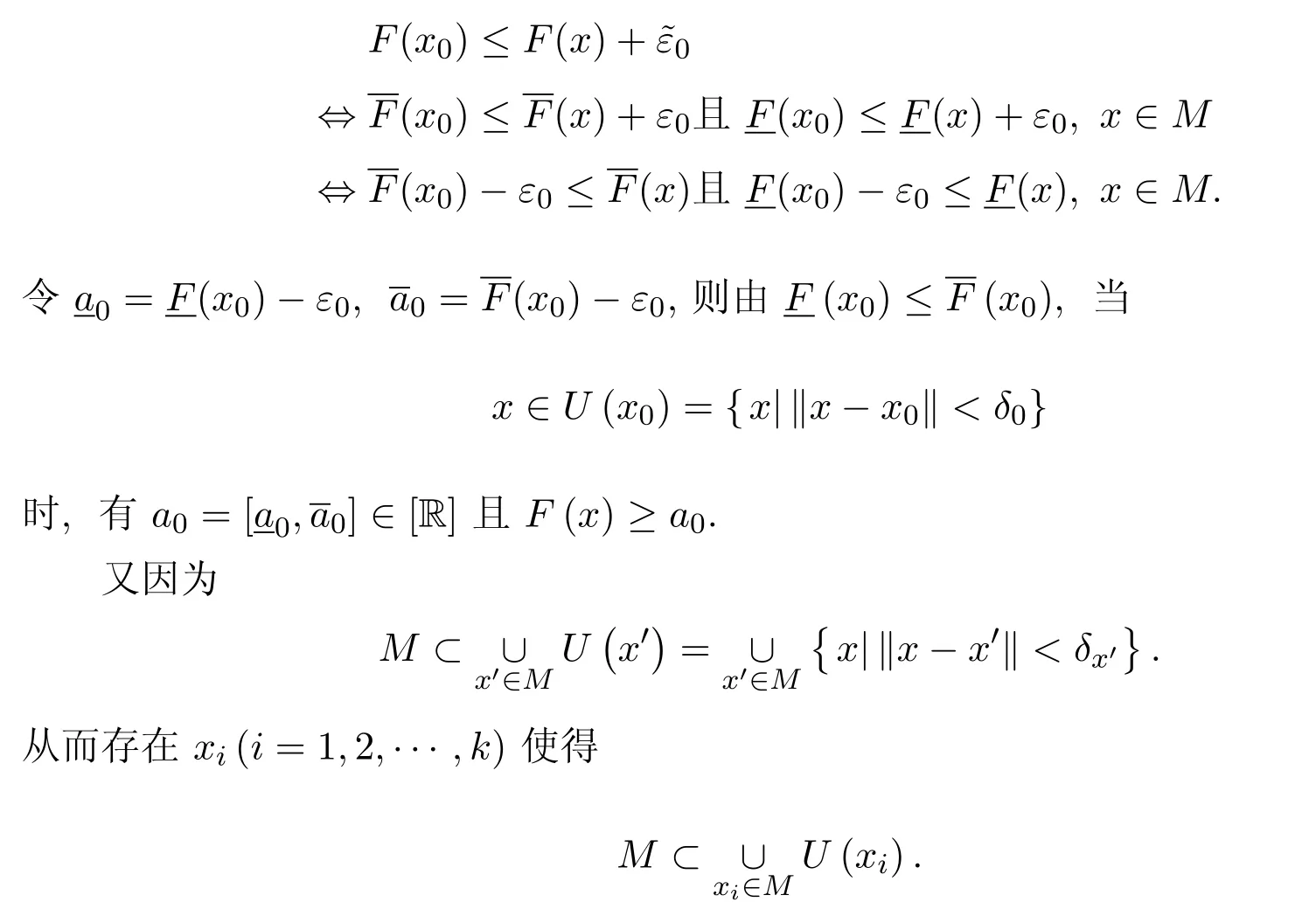
同理可证有界闭集的上半连续区间值映射有上界.

定理 3.4设F和G都是M上的上(下)半连续区间值映射,则F+G是M上的上(下)半连续区间值映射.

证明设F和G都是M上的上半连续区间值映射,x0∈M,则对任意ε>0,存在δ1>0,δ2>0,使得当x∈M且‖x−x0‖<δ1时,有

当x∈M且‖x−x0‖<δ2时,有

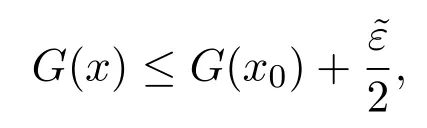
取δ=min{δ1,δ2},则当x∈M且‖x−x0‖<δ时,有

从而(F+G)(x)≤(F+G)(x0)+,即F+G是M上的上半连续区间值映射.

关于下半连续的情况证明类似于上半连续,从略.

称F:M→[R+]为非负区间值映射,关于非负区间值映射有下面的结论.

定理 3.5设F和G都是M上的非负上半连续区间值映射,则F·G也是M上的上半连续区间值映射.

证明设F和G都是M上的非负上半连续区间值映射,对x0∈M及0<ε<1,令

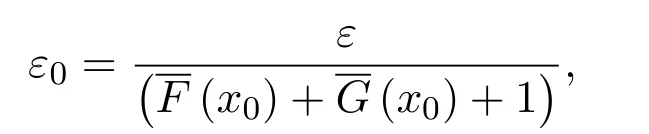
则 0<ε0<1且存在δ1>0和δ2>0使得当x∈M且‖x−x0‖<δ1时,有

当x∈M且‖x−x0‖<δ2时,有

取δ=min{δ1,δ2},则当x∈M且‖x−x0‖<δ时,由F和G的非负性有

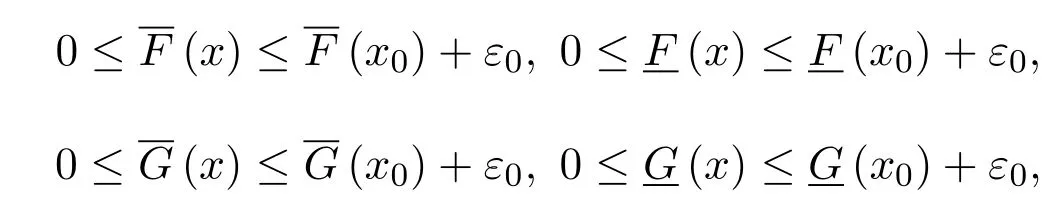
从而

4 区间值映射的凸性

本节讨论半连续区间值映射的凸性问题.在本节中设M是n维欧式空间Rn的一个非空凸子集.首先将引理2.2推广到区间值映射,给出下面的一个引理.

引理 4.1设F:M→[R]是一个区间值映射,如果存在α∈(0,1),使得

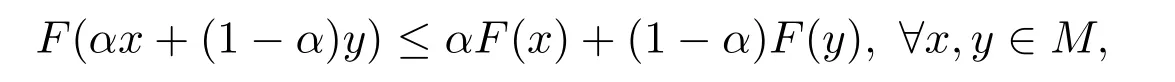
则数集

在[0,1]中稠密.

证明证明与文献[12]中定理2的证明类似,从略.

定理 4.1设F:M→[R]是下半连续区间值映射,如果存在α∈(0,1)使得

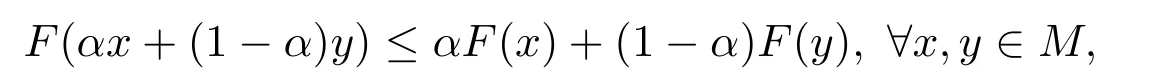
则F是M上的一个凸区间值映射.

证明对λ ∈(0,1),由引理 4.1可知存在点列λn∈K(n=1,2,···),使得

又由F的下半连续性及‖(λnx+(1−λn)y)−(λx+(1−λ)y)‖→0(n→ ∞)可得,对任意ε>0,存在N∈N+,当n>N时,有

于是由λn∈K,有

所以

从而由ε的任意性,当n→∞时有

即

因此F是M上的一个凸区间值映射.

定理 4.2设F:M→[R]是上半连续区间值映射,如果存在α∈(0,1)使得

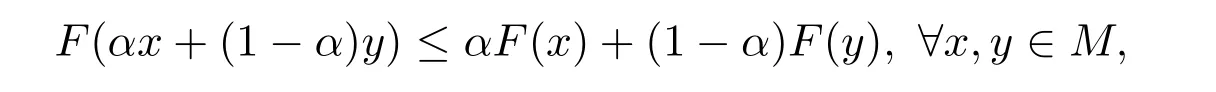
则F是M上的凸区间值映射.

证明对于λ∈(0,1),由引理4.1,可以选取单调递增点列λn∈K(n=1,2,···),使得λn→λ(n→∞),则

对x,y∈M,令s=λx+(1−λ)y,且

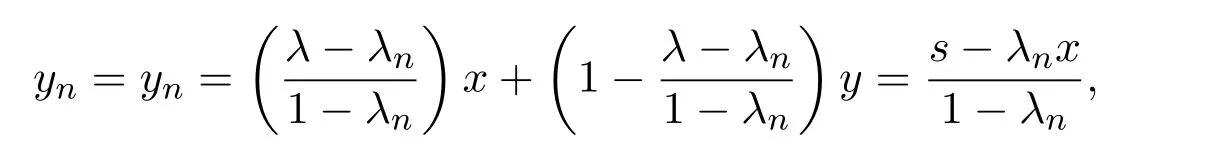
则s,yn∈M且

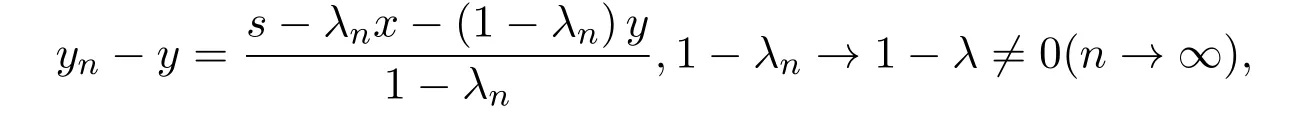
所以

另一方面,对任意ε>0,存在N∈N+,当n>N时,有

又由λn∈K,有

从而

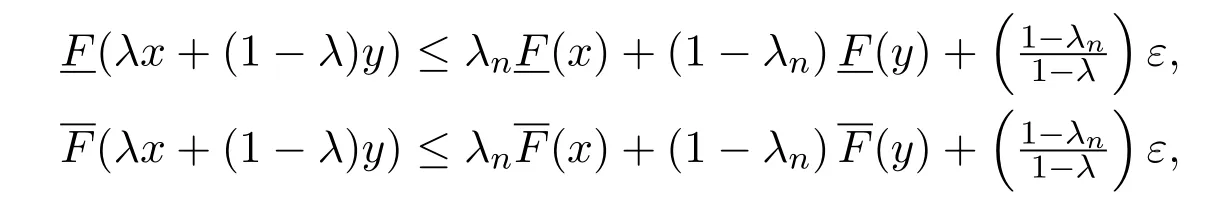
由ε的任意性,当n→∞时有

于是由区间数的序关系,有F(λx+(1−λ)y)≤λF(x)+(1−λ)F(y),∀x,y∈M.因此F是M上的凸区间值映射.

定理 4.3设M是闭凸集,F:M→[R]是下半连续区间值映射.如果对任何x,y∈M,存在λ ∈(0,1)使得F(λx+(1−λ)y)≤ λF(x)+(1−λ)F(y),则F是M上的凸区间值映射.

证明设F:M→[R]下半连续,则由定理3.2,(x)和(x)是闭凸集M上下半连续的实值函数.于是由实分析的性质,(x)和(x)的上图

都是Rn+1中的闭集.

如果对任何x,y∈M,存在λ∈(0,1)使得

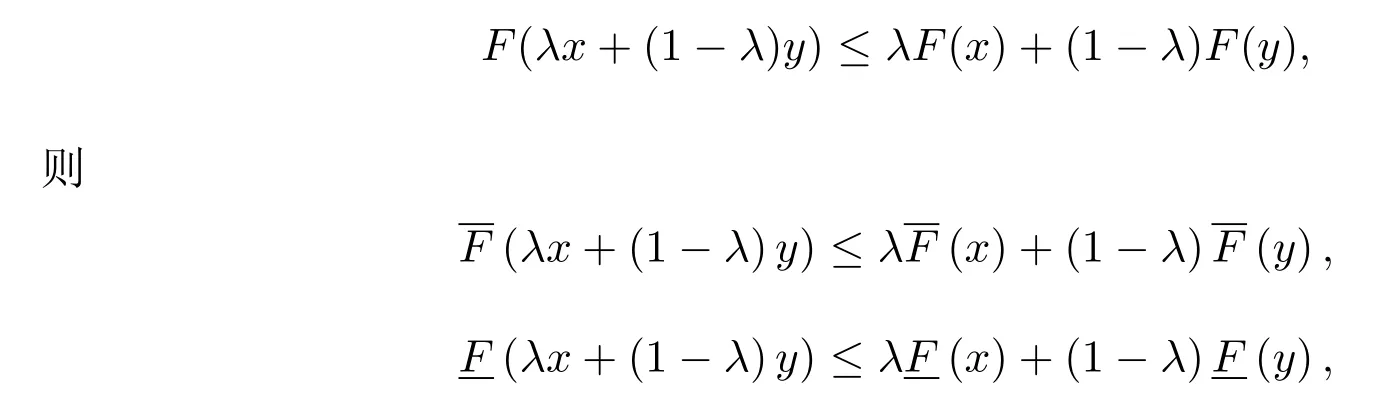
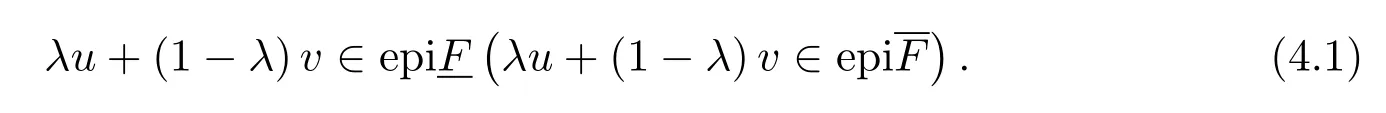
假设F:M→[R]不是凸区间值映射,则存在x,y∈M及λ0∈(0,1)使得

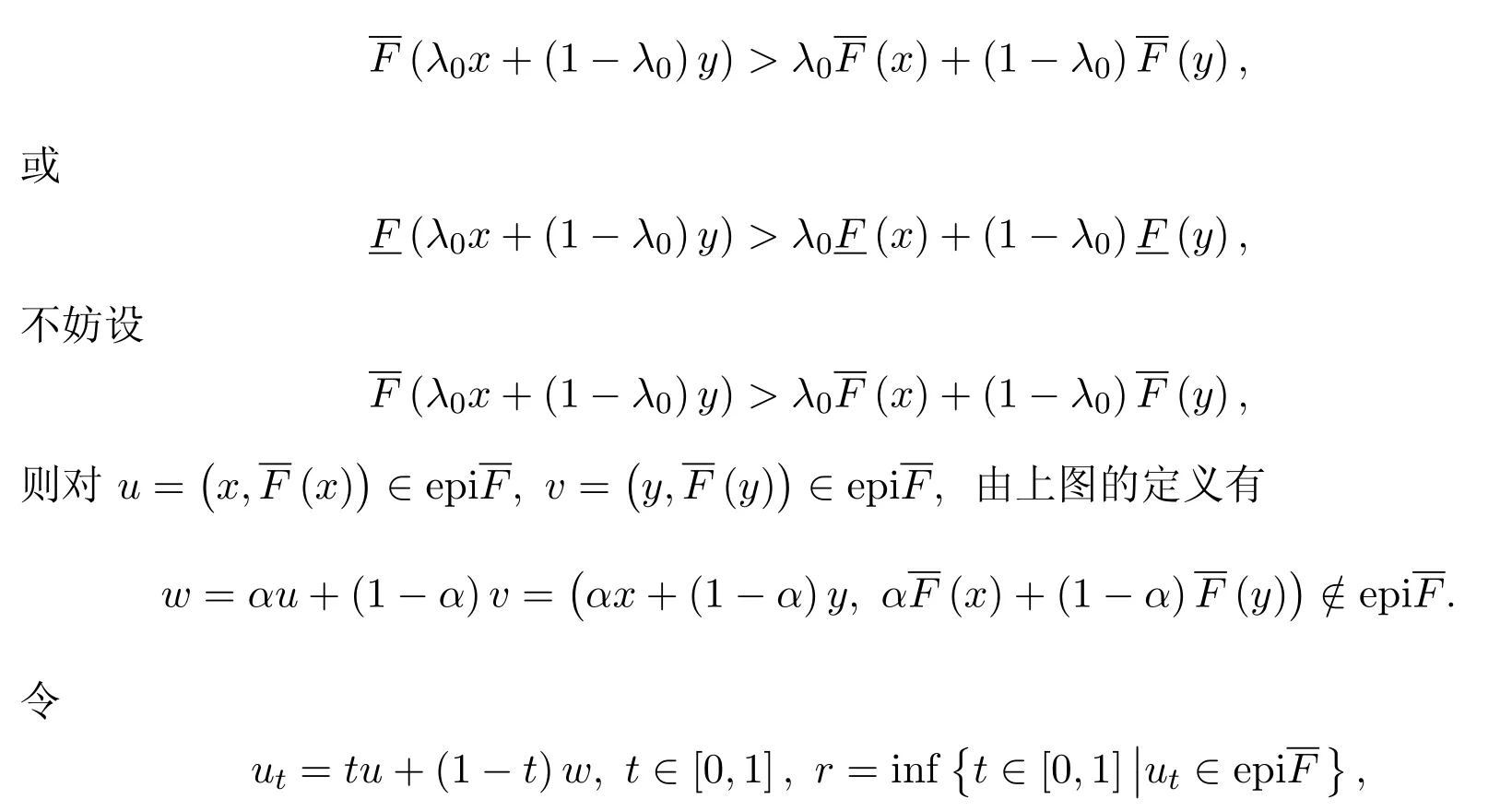
则存在{tn}∈[0,1]使得utn∈epi且tn→r(n→∞).于是由ut在点r∈[0,1]处的连续性及 epi的闭性,有ur∈epi.又由u0=epi,有r>0.从而当t∈[0,r),有utepi.

另一方面,令

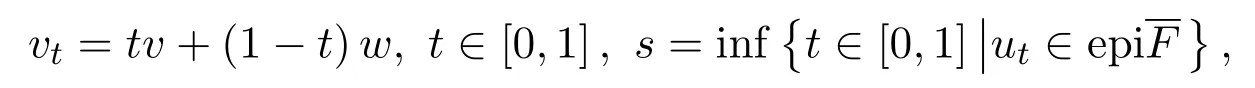
则同样vs∈epi且s>0,使得当t∈[0,s)时,有vtepi.从而对任何λ∈(0,1),有

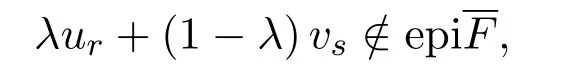
这与(4.1)式相矛盾.即F:M→[R]是凸区间值映射.

注 4.1在定理4.3中,当F:M→[R]是上半连续时,定理的结论也成立.