基于冗余紧框架的ℓ2/ℓ1极小化块稀疏压缩感知

张枫,王建军

(西南大学数学与统计学院,重庆 400715)

1 引言

压缩感知[1-3](compressed sensing)作为一种新的采样理论,它利用信号的稀疏特性,在远小于Nyquist采样率的条件下,用随机采样获取信号的离散样本,通过非线性重建算法完美地恢复信号.压缩感知理论一经提出,就引起了学者广泛关注.目前已在压缩成像[4],医学成像[5],模式识别[6],图像处理[7]等领域得到了广泛应用.

在压缩感知中,主要考虑以下模型:y=Ax+w,其中,A∈Rm×n是测量矩阵,y∈Rm是已知的线性测量,x∈Rn是待重构的未知信号,w∈Rn是噪声(‖w‖2≤ε).压缩感知的核心思想是依赖于信号是否是稀疏的或者近似稀疏的,即信号x的非零元素的个数是否远小于x的长度.然而,在现实中常见的自然信号不一定都具有稀疏特性,甚至这类信号在某些正交基上都不能够进行稀疏表示.自然地,上述信号重构过程不能直接应用于自然信号的重构.研究表明,一些自然信号在某些紧框架D∈Rn×N(n≤N,DD∗=In)[8-9]上能够稀疏表示,即x=Dα,其中α ∈RN是(近似)稀疏的.从数学的角度讲,上述问题可以写成以下形式

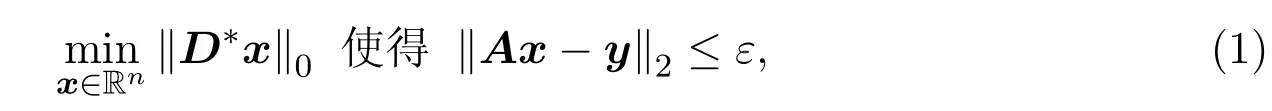
其中D∗表示矩阵D的共轭转置,‖D∗x‖0表示向量D∗x中非零元素的个数,若‖D∗x‖0≤k,那么就称向量D∗x为k-稀疏信号.由于问题(1)是一个 NP-hard问题,即在多项式时间内,计算机无法有效求解.所以一种更为实际的和易于处理的凸优化方法被提出

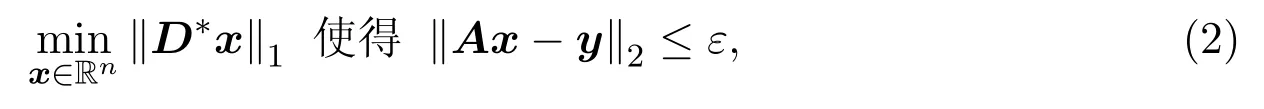
定义 1.1对于任意k-稀疏信号v(‖v‖0≤k),若存在 0<δk<1,使得

那么称矩阵A满足k阶D-限制性等容性质(D-RIP),最小的δk称为D-限制性等容常数(D-RIC).

进一步,他们指出当测量矩阵A满足D-限制性等容性质且δ2k<0.08时通过求解有约束优化问题(2)可以实现信号的鲁棒重构.之后,文献[11]将上述条件作了进一步改善,得到δ2k<0.4931.已知问题(2)可以转换为以下无约束优化问题

文献[8]提出,若A满足D-限制性等容性质(D-RIP),D是一个紧框架,当D-RIP常数δ2k<0.1907并且时,问题(3)的解满足

其中‖D∗x−(D∗x)k‖1是最佳k-项ℓ1逼近误差.C1,C2是两个数值型常数并且C1由 D-RIP 常数和‖D∗D‖1,1:=sup{‖D∗Dv‖1:v∈RN,‖v‖1≤1} 共同量化,C2仅取决于D-RIP常数.

然而现实世界中的自然信号其结构千变万化,一种常见的结构方式是自然信号在某些冗余字典下是块稀疏的,即其非零元素以块的形式出现,例如彩色图像处理[7]和 DNA-微列阵[12]等.从数学的角度看,给定分块τ={τ1,τ2,τ3,···,τd},对于任意向量α∈RN都可以被描述为

其中α[i]表示向量α的第i个子块,而αi则表示向量α的第i个分量元素.如果向量α最多有k个非零块,即‖α‖2,0≤k,则称向量α为块k-稀疏信号.特别地,当d=1时,等价于传统的带字典的压缩感知问题.相应地,测量矩阵A∈Rm×n和冗余字典D∈Rn×N也可以分别被描述为

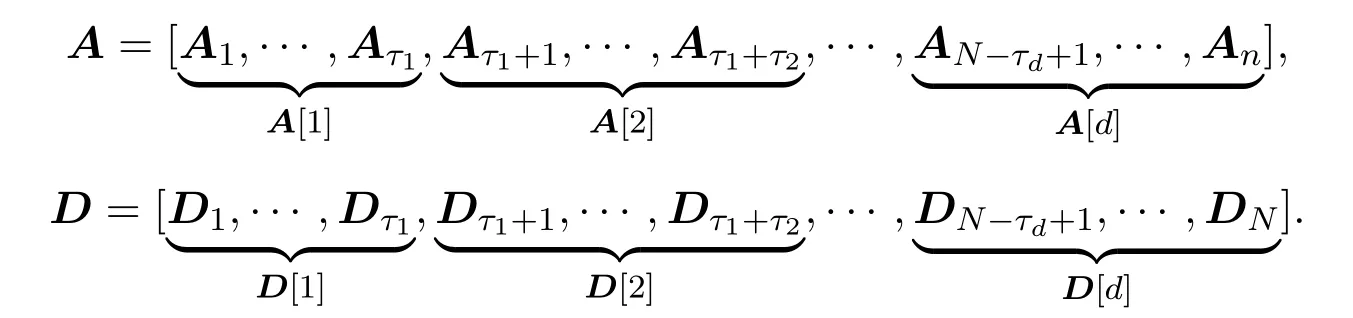
其中A[i],D[i]分别表示矩阵A和D的第i个子块(矩阵),而Ai,Di则分别表示矩阵A和D的第i个列向量.

然而使用原始的ℓ1极小化方法来恢复此类块稀疏信号不能充分利用信号的结构性特征,即非零元素是以块的形式出现的这一特性.为此,一些学者对传统的压缩感知方法进行了针对性的改进.文献[13]提出并研究了如下的ℓ2/ℓ1问题

定义 1.2对于任意块k-稀疏信号v(‖v‖2,0≤k),若存在 0<δk|τ<1,使得

那么称矩阵A满足k阶 Block D-限制性等容性质 (Block D-RIP),最小的δk|τ称为Block D-限制性等容常数(Block D-RIC).

文献 [14]指出当测量矩阵A满足 Block D-限制性等容性质 (Block D-RIP)且δ2k|τ<0.4142时,块稀疏信号能够通过求解有约束优化问题(4)进行鲁棒重构.其后,文献[15]将上述条件作了进一步改善,得到了δ2k|τ<0.4931.类似地,问题(4)可以转化为以下块无约束优化问题

假设A满足Block D-限制性等容性质(Block D-RIP),D是一个紧框架,本文研究表明,当 Block D-RIP 常数δ2k|τ<0.2 并且时,问题(5)的解满足

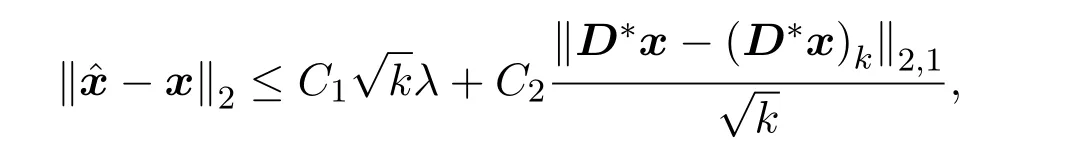
其中C1,C2是两个数值型常数并且C1由D-RIP常数和

共同量化,C2仅取决于D-RIP常数.

2 预备知识

为了方便介绍后文,首先给出以下记号.

•给定正整数d,记索引集T⊂{1,2,···,d}且|T|=k,Tc表示T在{1,2,···,d}中的补集.

•DT∈Rn×|T|表示从D中取出索引集T对应的列所组成的矩阵,记

•记T1为包含的k个最大2范数块的索引集,T2为包含的k个最大2范数块的索引集,等.

接下来,为了证明主要定理,需要以下引理.

引理 2.1

证明由Tj的构造,有

上式两边取2范数,得

所以,有

引理2.2令测量y=Ax+w,h=−x,若,则问题(5)的解满足

证明由实值凸的低阶半连续函数的次微分的定义和是问题(5)的解可知,满足问题(5)的子梯度最优化条件,即

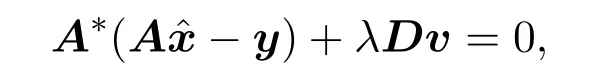
其中v∈RN,若,则,否则‖vi‖2≤1.因此存在v∈RN使得‖v‖2,∞≤1,进一步,有

引理得证.

引理 2.3令D∈Rn×N为满足DD∗=In的矩阵,A∈Rm×n为满足Block DRIP条件的矩阵.令索引集T⊆{1,2,···,d}恰有k个块,测量

证明令T0为包含D∗h的k个最大2范数块的索引集,因为,所以取T=T0就能充分证明该引理.

因为A满足 Block D-RIP条件,不失一般性,假设存在

使得‖u‖2=‖c‖2=1,因此有

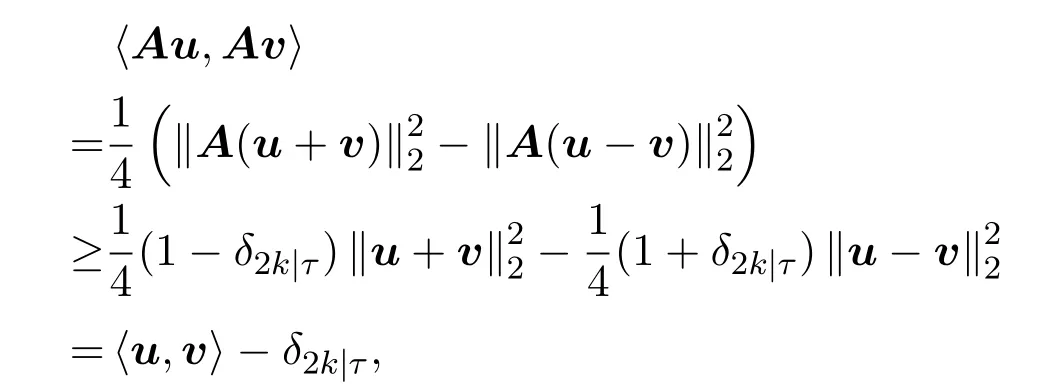
注意到D是一个紧框架,即DD∗=In,故

因此

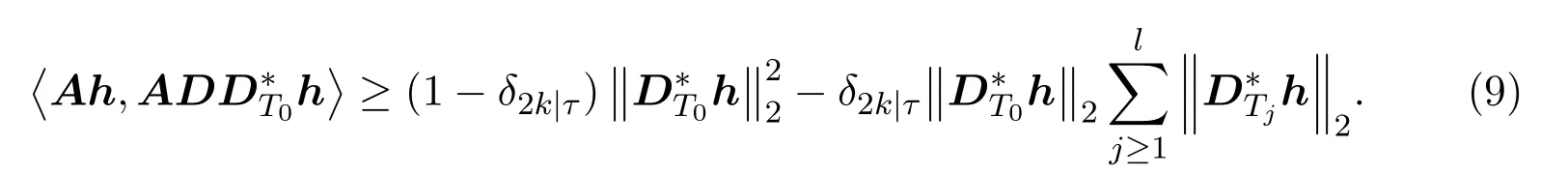
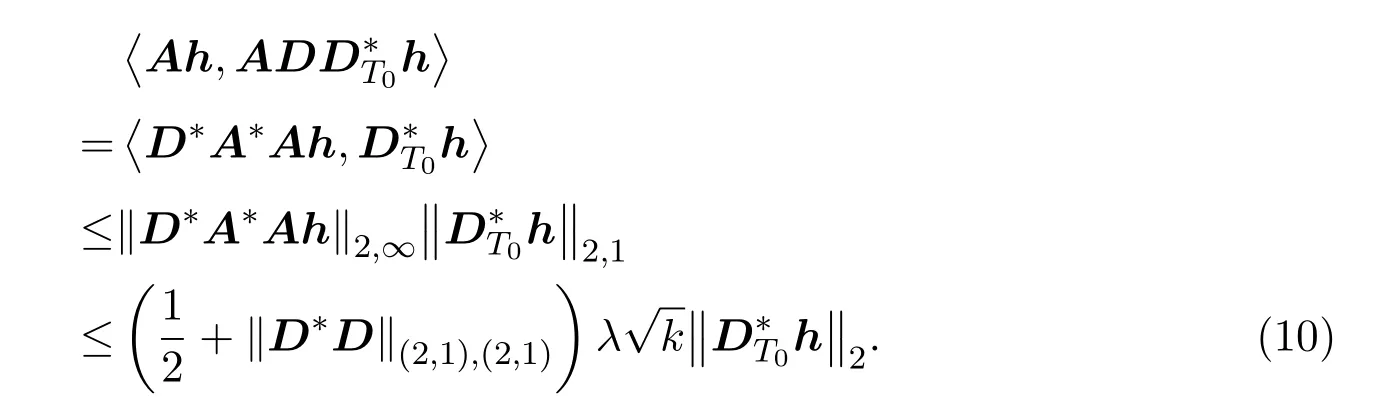
结合(6)式,(9)式-(10)式,有

引理得证.

引理2.4令D∈Rn×N为满足DD∗=In的矩阵,测量y=Ax+w,h=，若,则问题(5)的解满足

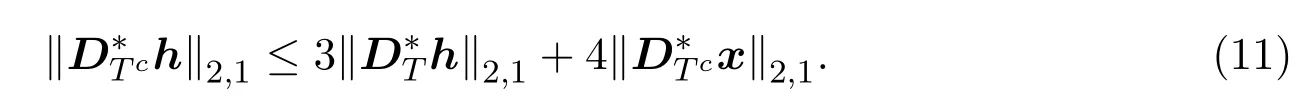
将h=−x,y=Ax+w代入上式,由D是一个紧框架可知

由三角不等式,易知

整理后得(11)式,引理得证.

3 主要结果

定理 3.1令D∈Rn×N为满足DD∗=In的矩阵,A∈Rm×n为满足Block DRIP(0<δ2k|τ<0.2)条件的矩阵,(D∗x)k为由D∗x的k个最大 2范数块组成的向量,测量y=Ax+w,h=−x,若,则问题(5)的解满足

证明由引理2.1和引理2.4,有

由于 1−3β2>0(0<δ2k|τ<0.2),故

由 (8)式和 (14)式,有

由(13)式-(15)式知,(12)式成立.

4 数值实验

为了验证理论结果,本文分别做了两组实验:(a)设计满足定理3.1条件的算法;(b)理论误差上界对比实验.实验在CPU为Inter(R)Core(TM)i3,内存为2GB的台式电脑上进行,运行软件为MATLAB(R2014a).实验中,测量矩阵A∈R128×256服从标准高斯分布,字典D∈R256×1024由傅里叶变换矩阵和单位矩阵合并而成,并且满足DD∗=In,测量误差w∈R128服从正态分布,取正则化参数λ=1e−3,从而满足,待重构的信号为x∈R256,在字典D下的块稀疏信号α∈R1024中的非零块位置随机产生.为了克服实验结果的偶然性,所有实验将独立重复地进行100次.在本文中,将冗余字典和Block-IRLS算法[16-18]相结合提出D-Block-IRLS算法:输入:分块τ={τ1,τ2,···,τd},测量矩阵A,字典D,观测信号y,块稀疏度估计k.

输出:重构信号x.

(a)选择适当的惩罚参数λ(0<λ<1).

(b)初始化迭代向量α(0),使其满足ADα(0)=y.设置ϵ0=1.

(c)开始迭代j=0.

(d)通过α(j)解决下面的线性问题

(e)当α(j)满足停机条件,将Dα(j)作为输出赋值给x,同时结束算法,否则执行下一步.

其中,r(α)表示将向量α的分块取ℓ2范数后,再由大到小依次排列形成的向量.而r(α)k+1表示向量r(α)的第k+1个分量值.

(g)j=j+1,并返回到第4步继续执行.

首先针对D-Block-IRLS算法,采用两种分块形式,均分256块和非均分256块.图1分别研究了均匀分块和非均匀分块的情况下通过D-Block-IRLS算法得到的误差‖−x‖2以及理论误差上界与块稀疏度k的关系.由图可知,无论是均匀分块还是非均匀分块通过D-Block-IRLS算法得到的误差都远小于理论误差上界,换言之,利用D-Block-IRLS算法来重构块稀疏信号可以满足实验设计的需要并且从侧面印证了本文理论分析的正确性.

图1 D-Block-IRLS算法误差与理论误差上界对比

由文献 [8]知,当D∈Rn×N为满足DD∗=In的矩阵,A∈Rm×n为满足 DRIP(0<δ2k<0.1907)条件的矩阵,(D∗x)k为由D∗x的k个最大元素组成的向量,测量

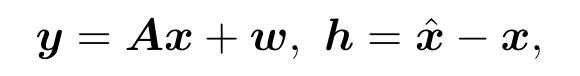
现在分别用块和非块的方式来处理块稀疏信号α,取

其他参数保持一致[9].图2表明,无论是均匀分块还是非均匀分块,所获理论误差上界都明显优于(16)式的误差上限.

5 小结

本文采用ℓ2/ℓ1极小化方法研究了基于冗余紧框架下的块稀疏信号的恢复,获得了该方法鲁棒重构原始信号的充分条件和误差上界估计,所获结果表明,误差上界可以通过正则化参数λ,k-项逼近和块稀疏度来控制.仿真实验证明了理论结果的准确性,该结果对于推动压缩感知的进一步发展具有一定的理论价值和借鉴作用.