非结构网格下2D Riesz分数阶方程的Galerkin有限元方法

卜玮平

(湘潭大学数学与计算科学学院,湖南 湘潭 411105)

1 引言

最近,分数阶微分方程数值方法的研究越来越受关注.有限差分方法(FDM)是求解分数阶微分方程最常见的数值方法之一.文献[1]是研究FDM求解分数阶微分方程数值方法的先驱.随后,利用有限差分方法人们对各种分数阶微分方程进行了求解[2-5].谱方法(SM)和谱元方法(SEM)是求解分数阶微分方程的重要方法,它们通常具有很高的收敛精度.目前,SM和SEM求解分数阶微分方程的工作有文献[6-8]等.相比于FDM方法和SM(或SEM)方法,有限元方法(FEM)的主要特征是它能够较易处理复杂区域且对解的光滑性要求较低.文献[9]首次尝试用有限元方法求解分数阶微分方程,并给出了有限元逼近的理论框架.此后,文献[10]建立了有限元求解一维和二维分数阶对流弥散方程的理论框架.随后,在有限元求解分数阶微分方程方面涌现了越来越多的工作,其中包括文献[11-15]等.

近年来,关于二维分数阶微分方程的有限元方法也有一些研究成果.文献[10]考虑了基于分数阶方向导数的二维分数阶对流-弥散方程的有限元方法.通过使用矩阵转换技术,文献[16]讨论了基于分数阶拉普拉斯算子的二维分数阶扩散方程有限元方法.文献[17]发展了基于分数拉普拉斯算子的分数阶扩散方程自适应有限元方法.为了求解二维Risez/Riemann-Liouville分数阶扩散方程(2DRFDE/2DRLFDE),基于一致三角网格剖分,文献[18-19]考虑了Galerkin有限元方法.然而,对于不规则区域上2DRFDE/2DRLFDE的有限元方法,通常需要采用非结构网格.基于非结构网格,文献[20]利用三角形上定义的Lagrange多项式,建立了2DRLFDE的间断Galerkin方法.文献[21]考虑了非线性2DRFDE的有限元方法,并描述了有限元方法的实现.文献[22]讨论了二维时空分数阶波方程在非规则凸域上的有限元方法.

尽管在文献[20-22]中已有非结构网格下有限元求解分数阶微分方程的工作,但是这些工作使用的是相同的有限元实现技巧.值得注意,上述文中提到的有限元实现方法有不足之处.因此,在这篇文章中将提出一些新的技巧,以改进现有的有限元实现方法.本文的主要贡献如下:首先,对于刚度矩阵的计算降低了计算花销,原来的计算花销为O(Ne3),现在的花销为O(Ne2),Ne为总剖分单元数;其次,提高了刚度矩阵的元素的精度,对于三角形单元的高斯积分,不同于现有的计算方法,高斯积分区域为被积函数的非零的区域,这比由以往方法得到的刚度矩阵元素更精确;第三,将Riemann-Liouville导数转化为Caputo导数,简化了内积的计算.

本文的结构安排如下:在第2节,给出了分数阶导数的定义、模型问题及有限元全离散格式的推导;在第3节,首先介绍了现有的刚度矩阵计算方法,然后详细描述了有限元的实现方法,并与现有方法进行了比较;在第4节,给出了数值实验来证明方法的有效性;最后,对本文进行了总结.

2 准备工作

令Ω⊂R2,则x,y方向的左右Riemann-Liouville分数阶导数定义如下:

其中γ,n−1<γ≤n,n∈N,a(y),b(y),c(x),d(x)定义如图1.

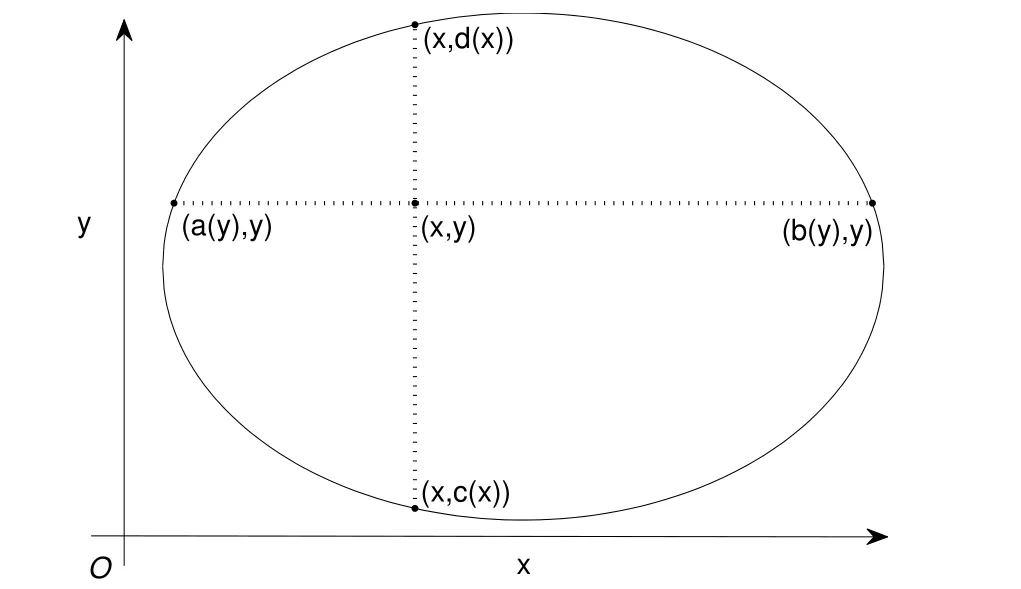
图1 关于Ω上a(y),b(y),c(x),d(x)的定义

进一步,定义x,y方向的γ(1,3,···)阶 Riesz分数阶导数如下

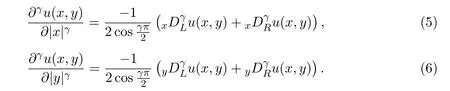
类似地,x,y方向γ阶右Caputo分数阶导数定义如下

在文献[23]中已经讨论了Riemann-Liouville分数阶导数和Caputo分数阶导数的等价关系,如果u(a(y),y)=0,u(x,c(x))=0,0<γ<1,则

本文考虑如下分数阶扩散方程

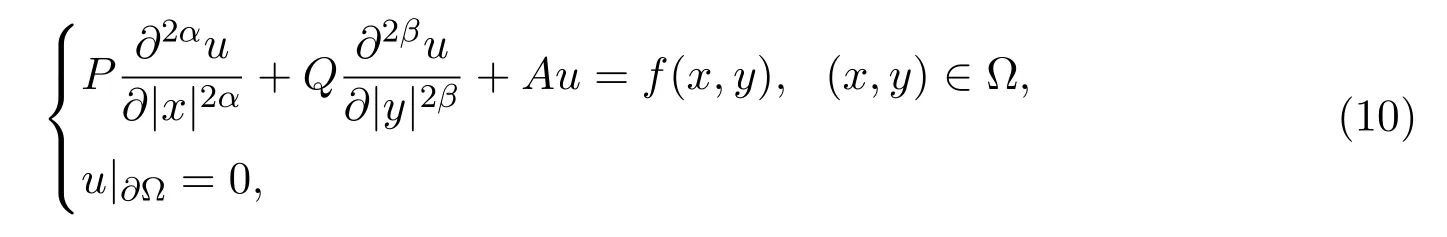
对上述方程,首先考虑其变分形式和有限元全离散格式.对于任意γ≥0,记γ(Ω)为Hγ(Ω)的子集且其元素在 Ω 外的零扩张属于Hγ(R2).令V=α(Ω)∩β(Ω).于是,由文献[18]中引理5可得如下变分问题:寻找u∈V使得

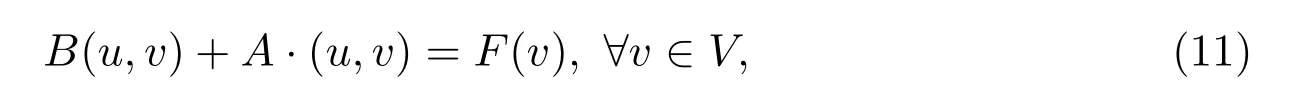
其中 (·,·):=(·,·)L2(Ω),F(v):=(f,v),且

为了得到上述变分问题的全离散格式,先将Ω进行剖分.令{Th}是Ω的一个正则的三角剖分,h为所有三角形单元的最大直径.定义如下有限元空间

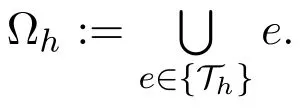
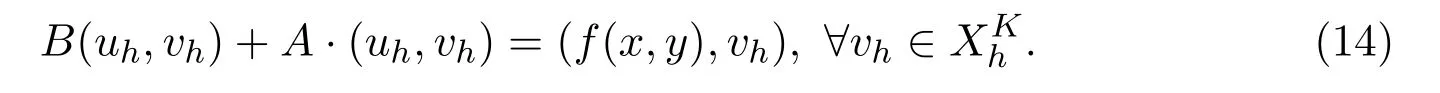
3 有限元方法的实现

为了计算全离散格式(14),需要计算刚度矩阵和荷载向量.由于分数阶导数为非局部算子,与整数阶微分方程相比,其主要区别在于分数阶微分方程刚度矩阵的计算非常复杂.因此,方法实现的重点将放在刚度矩阵的计算上.

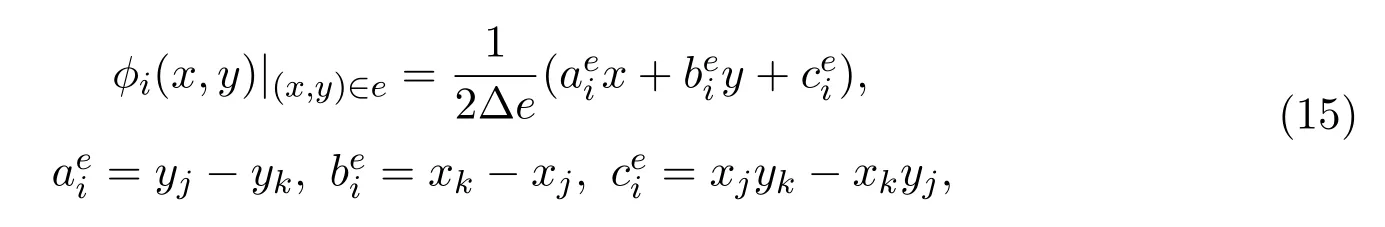
这里∆e为三角形单元e的面积,(xi,yi),(xj,yj),(xk,yk)是对应顶点i,j,k的坐标.

接下来,考虑B(uh,vh)的计算.令

这里S={Sij}N×N为刚度矩阵,其元素为

3.1 已有的实现方法

目前,文献[20-22]已经考虑了Sij的计算.然而,应该注意这些文章关于Sij的计算方法是类似的.这里简单对文献[20-22]中Sij的计算方法进行描述.由于(17)中四个内积的计算具有相似性,因此仅仅以为例进行讨论.考虑分数阶算子的非局部性并利用高斯积分可得

这里Ge为三角形单元e上的高斯点,ωl是高斯点(xl,yl)对应的权重.

上面(18)式中的方法可以用来计算Sij,然而该方法有三点不足之处.令Ne为剖分三角形单元的总数.首先,对于Sij的计算需要考虑如下积分在每个三角形单元的高斯积分

因此,为了得到刚度矩阵的一个元素Sij,上述积分需要进行Ne次,而为了获得整个刚度矩阵,需要计算次,这将使得刚度矩阵的计算花销随Ne的增涨而快速增涨.其次,对于下列积分

考虑被积函数在三角形单元上的非零区域.由于分数阶算子具有非局部性,显然存在满足下列情形的三角形单元:被积函数在三角形的某些部分为零,在其他部分非零.因此,被积函数在满足上述条件的三角形单元上为间断函数.如果对这些单元,在整个三角形上运用高斯积分势必达不到数值积分的相应精度.图2给了描述上述情形的例子(图形(a)描述了的非零区域,其中ϕi为节点i的基函数,ϕk为节点k的基函数;图形(b)描述了被积函数的非零区域,它为支集的交集).

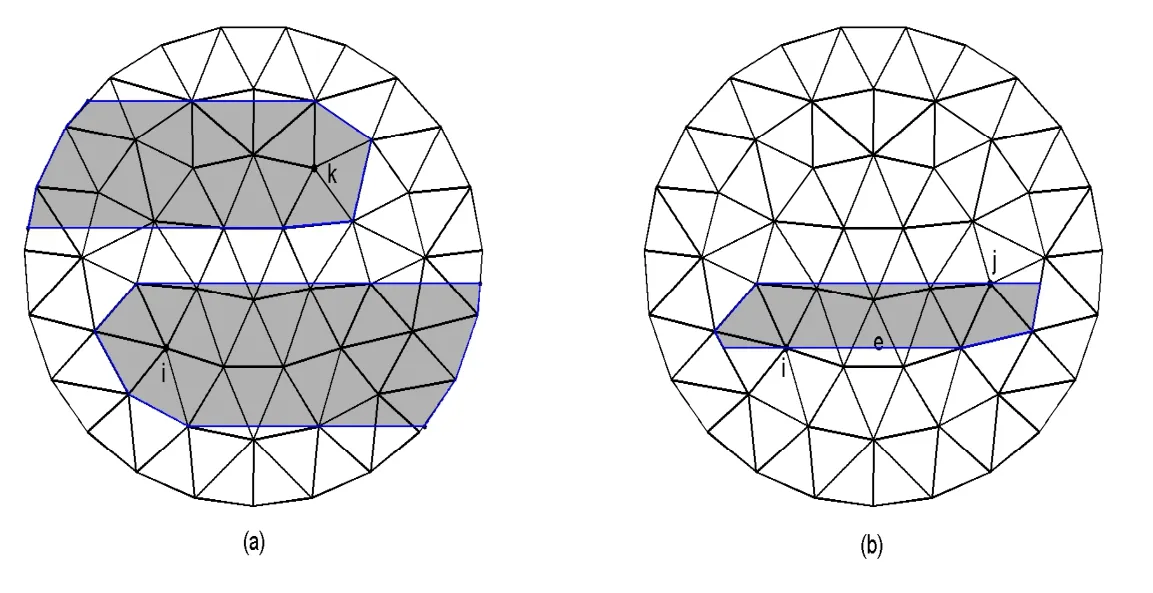
图2 的非零区域和 的非零区域

图3 在(xp,yp)的计算结果

计算ϕi(x,y)的左Riemann-Liouville分数阶导数在(xp,yp)点的值

3.2 实现方法

针对已有方法的不足,设计一种新的求解二维Riesz分数阶扩散方程的有限元实现方法.因为,显然

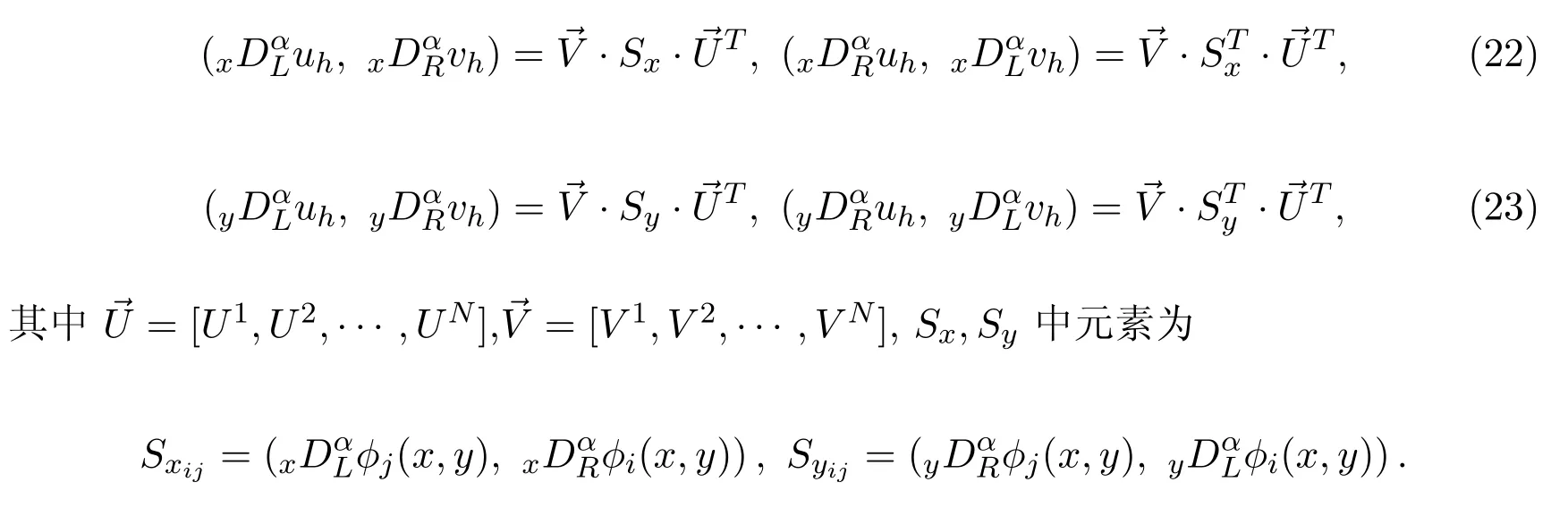
因此,为了计算(16)中刚度矩阵S,根据对称性仅需要计算Sx和Sy.

图4 Lagrange线性基函数ϕi(x,y),ϕj(x,y)的支集

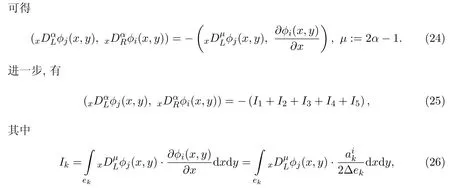
为了计算积分Ii,已有的方法是在整个三角形单元ei上使用高斯积分.然而,上面已经提到这样做将降低高斯积分的效果,因为分数阶算子具有非局部性,的非零区域在某些单元可能只占有一部分(即在该单元为间断函数),如图5.

图5 的支集

图6 的支集

注意到,对于ϕi(x,y),由 (9)式可得

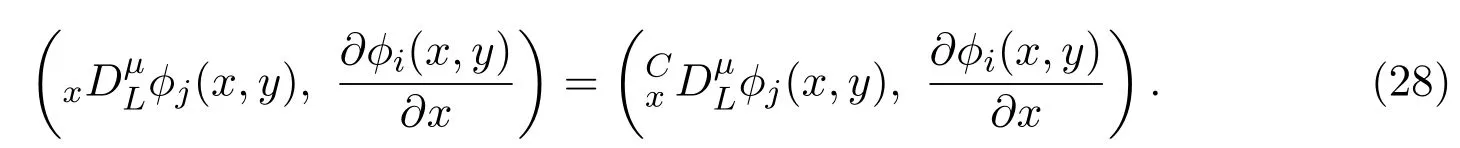
于是利用高斯积分有

这里e为的非零区域,ai,∆e定义在(15)式中.

假设ϕj(x,y)及其积分路径被定义在图3中,对于高斯点(xp,yp),有

显然(30)式比(21)式更容易计算.

4 数值实验

本节给出一个数值例子来验证方法的有效性.

例 4.1在模型方程(10)中,取P=Q=2,A=4.考虑如下两种情形:(a)假设考虑问题区域为[0,1]×[0,1],其精确解为u=100x2(1−x)2y2(1−y)2;(b)假设考虑问题区域为,其精确解为,相应的右端函数分别定义如下

当选择不同的α和β时,表1-表4分别列出了情形(a)和情形(b)所得的数值结果.

可以看出,所得误差的收敛率是最优收敛率.

表1 基于Lagrange线性多项式与α=0.6,β=0.6计算情形(a)的数值误差与收敛率

表2 基于Lagrange线性多项式与α=0.7,β=0.8计算情形(a)的数值误差与收敛率

表3 基于Lagrange线性多项式与α=0.7,β=0.6计算情形(b)的数值误差与收敛率

表4 基于Lagrange线性多项式与α=0.6,β=0.8计算情形(b)的数值误差与收敛率

5 总结

本文研究了非结构网格下利用Lagrange线性基函数求解2D Riesz分数阶扩散方程的有限元方法实现.首先,描述了现有有限元全离散格式的实现方法,并指出了现有方法的不足之处.随后,针对这些缺点设计了一种新的实现方法,提高了有限元方法的计算效率和刚度矩阵的精度.最后,给出了数值算例,数值结果验证了本文所提方法的有效性.