空间分数阶Schrödinger方程调制不稳定性的数值研究

李文斌,王冬岭

(西北大学数学学院,陕西 西安 710127)

1 引言

调制不稳定现象是非线性介质中普遍存在的现象,该现象的应用十分广泛,如声波的传递,水波的扩散,以及光学等很多领域[1].研究这种现象常用的模型为非线性薛定谔方程,该方程是弱非线性色散波演化的通用模型.在该非线性方程中,当满足Benjamin-Feir-Lighthill准则,即当非线性项和色散对该波的频率贡献相反,就会出现调制不稳定性.本文使用文献[2]中线性稳定性分析的方法来研究这种调制不稳定性是如何产生的.

文献[3]研究了整数阶薛定谔方程的这种不稳定现象,并且证实这种现象对于不同形式的薛定谔方程以及不同初值条件下都表现为相似的结构,即不稳定区域都是由两部分构成:中间是一个波动的楔形区域,两边分别是一个扇形的平面区域.

文献[4]研究了分数阶薛定谔方程的调制不稳定性,证明了分数阶拉普拉斯算子的指数α对带宽,增益谱,以及最大频率的影响.通常根据Benjamin-Feir-Lighthill准则验证调制不稳定性存在的条件.本文主要通过数值研究的方法把文献[3]中关于经典整数阶薛定谔方程调制不稳定性的主要结果和发现推广到空间分数阶薛定谔方程,并且分析和比较空间分数阶导数的阶α对于不稳定区域的各种影响.发现,当α=2时,得到和文献[3]中完全一致的结果,当该参数改变的时候,将显著影响不稳定区域的大小和形状.

首先验证如下整数阶薛定谔方程调制不稳定性的存在条件.

使用文献[2]中线性稳定性分析的方法来研究这种调制不稳定性产生的机制.首先,假设方程(1)存在稳态扰动解

其中P为初始频率,φ(x,t)为扰动项.将解(2)带入方程(1)可得

其中φ∗为φ的复共轭.方程(3)有形式解

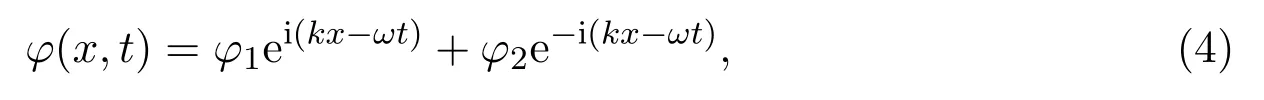
其中k为扰动波的个数,ω为扰动频率.将解 (4)带入方程 (3)并分离 ei(kx−ωt)和 e−i(kx−ωt)的系数可得方程组

结合两个等式可计算出ω关于k,P的关系式

由Benjamin-Feir-Lighthill准则[1]可知,当ω为实数时,该方程的稳态解u(x,t)是稳定的.当参数ω为复数时,该方程的状态解u(x,t)呈指数增长,即出现调制不稳定性,显然存在P>0使得ω为复数,此时该解为不稳定的.

本文主要研究空间分数阶非线性薛定谔方程在不同初值条件下的调制不稳定性.运用Strang分裂方法和傅里叶谱方法求出该方程的数值解,并与整数阶的方程进行比较,可以得出空间分数阶非线性薛定谔方程同样具有这种不稳定性.并给出了α取不同值时的数值结果.从而证实了空间分数阶薛定谔方程的调制不稳定性的存在性以及这种不稳定性的普遍行为.

近年来分数阶拉普拉斯算子应用十分广泛,因此将薛定谔方程中的拉普拉斯算子替换为分数阶拉普拉斯算子,分数阶拉普拉斯算子可以表示异常的扩散现象.因此本文中研究空间分数阶薛定谔方程是否仍具有和整数阶薛定谔方程类似的调制不稳定性.

分数阶拉普拉斯的定义[5-6]有多种,在文献[5]中,最常见的是如下的谱方法定义:

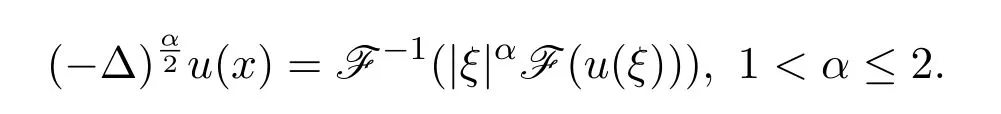
其中F,F−1为连续的傅里叶变换和傅里叶逆变换,当α=2时,即为经典的拉普拉斯算子.当1<α<2时,可知该分数阶拉普拉斯算子为非局部算子.

薛定谔方程是量子力学中的一个基本方程,它描述了粒子在空间中某一位置的概率.文献[7]从高斯分布,导出了整数阶薛定谔方程.文献[8]证明了存在另外的非高斯分布,即 Lévy-α稳定的概率分布.而布朗运动是Lévy-α稳定的随机过程,Laskin导出了分数阶薛定谔方程.描述这类过程的主要数学模型为分数阶拉普拉斯算子,用分数阶拉普拉斯算子代替整数阶拉普拉斯算子可以描述异常的扩散现象.由于分数阶拉普拉斯算子的非局部性,研究空间分数阶薛定谔方程是否仍然具有调制不稳定性,以及不稳定性存在的条件.

空间分数阶薛定谔方程有很多的应用,可参考文献[9-11].本文主要研究空间分数阶薛定谔方程

当α=2时,该方程即为常见的整数阶薛定谔方程.

2 空间分数阶薛定谔方程

本文主要研究空间分数阶薛定谔方程

主要研究以下三个初值

(8a),(8b),(8c)分别为三个不同的初值.由图1可以看出(8a)为高斯型初值,(8b)为正割型初值,(8c)为盒状初值,这三个初值都是在(−1,1)上波动,在两边均为常数.这样就可以随时将中间的波动区域与两边的常数区域作比较.

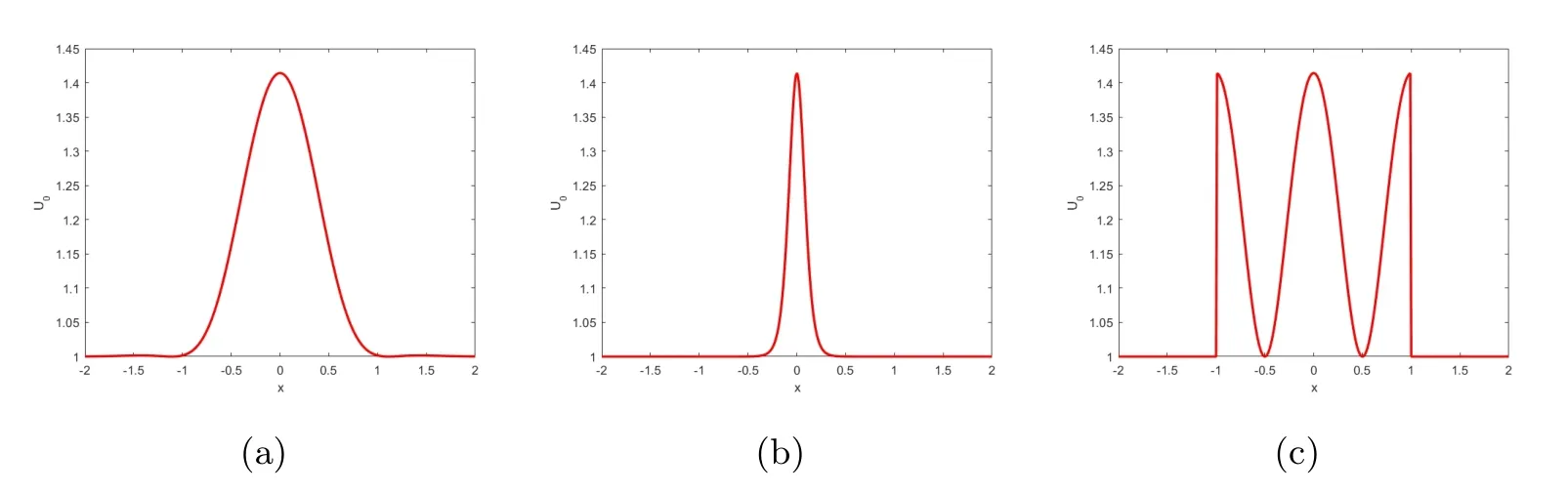
图1 初值(8a),(8b),(8c)

求解该方程的数值解法本文使用Strang分裂方法[12],该方法可将非线性偏微分方程分解为一个线性方程和一个非线性方程,从而方便计算偏微分方程中出现的非线性问题,然后将线性问题的解与非线性问题的解结合起来即可得到该方程的解.

3 空间分数阶 Schrödinger方程调制不稳定分析

由文献[4]的方法可知,假设方程(7)存在稳态扰动解

其中P为初始频率,φ(x,t)为扰动项.将解(9)带入方程(10)可得

其中φ∗为φ的复共轭.方程(10)有形式解

其中k为扰动波的个数,ω为扰动频率.将解(11)带入方程(10)可得

由于

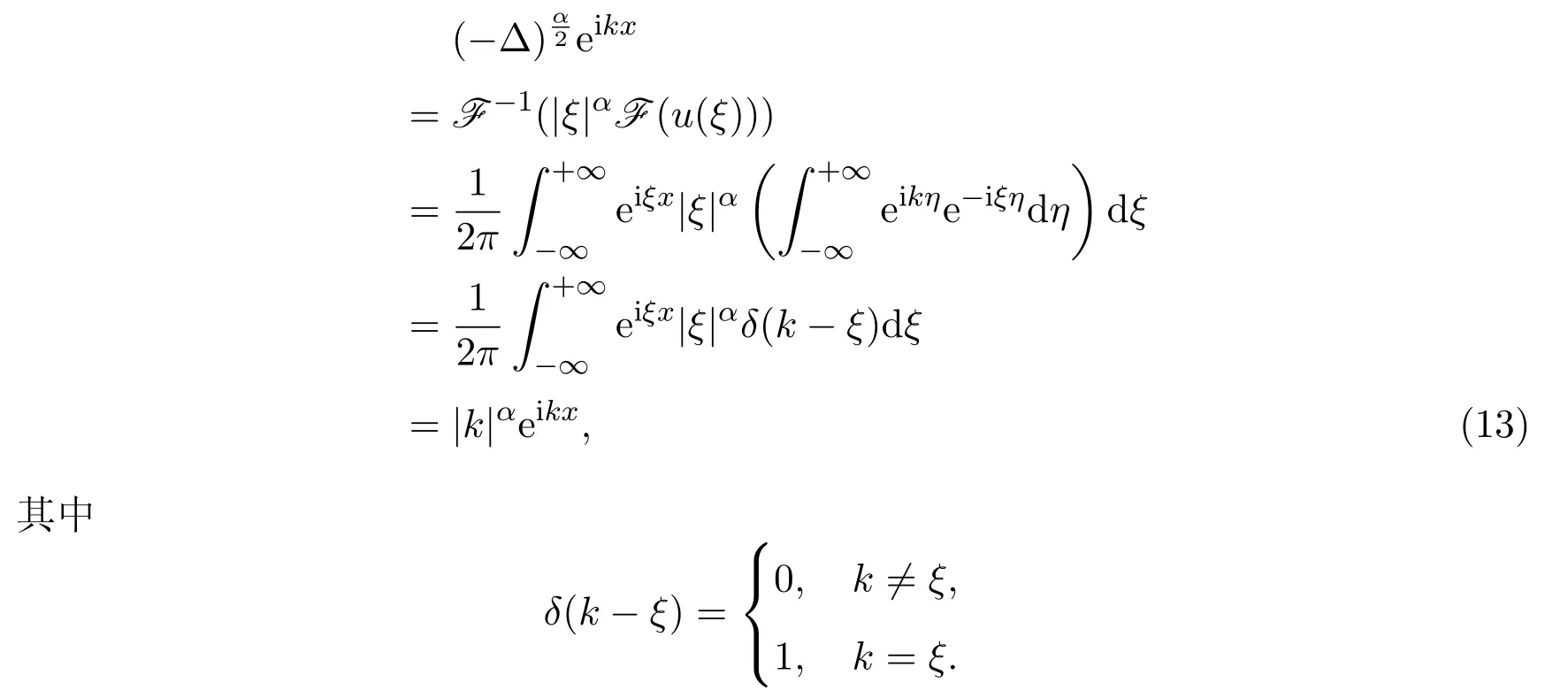
因此可将等式(12)两端作傅里叶变换后作傅里叶逆变换,并分离ei(kx−ωt)和e−i(kx−ωt)的系数可得方程组

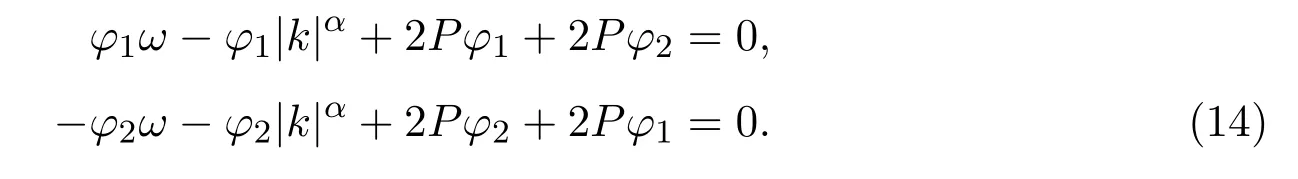
结合两个等式可计算出ω关于k,P的关系式

由 Benjamin-Feir-Lighthill准则可知,当ω为实数时,该方程的状态解u(x,t)是稳定的.当ω为复数时,该方程的状态解u(x,t)是不稳定的,即出现调制不稳定性,显然存在P>0使得ω为复数,此时解为不稳定的,且频率随α的变化而变化,即该不稳定性受α影响.

4 数值解法

应用分裂方法[13-14],可将薛定谔方程分解为

其中(16)为线性分数阶方程,(17)为非线性方程.由Strang分裂方法[12]得出该方程的解

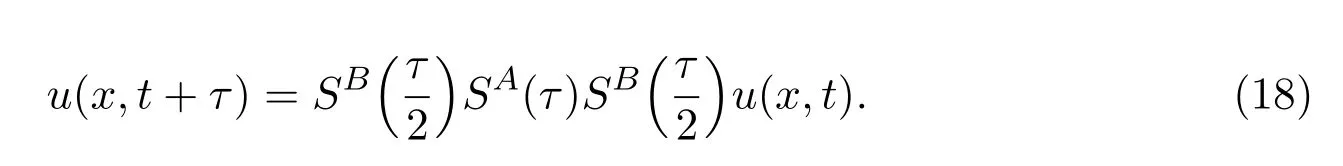
SA表示线性方程(16)的真解,SB表示非线性方程(17)的真解.

4.1 线性项处理

首先线性项(16),使用傅里叶级数展开形式

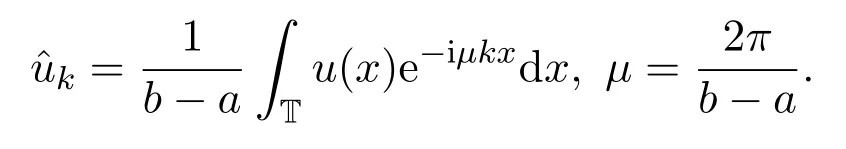
a,b为一个周期的两个端点,T表示周期,即T=[a,b],且u(a)=u(b).由文献[5-6]可知可表示为

线性项(16)可化为

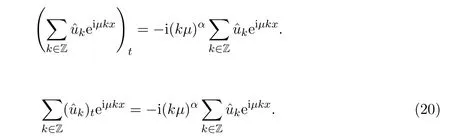
由指数函数的正交性可将上述方程化为

解常微分方程(21)可得

其中τ为时间步长,且um+1,um为第m+1和m层时间的数值解.截取令

将(22)式写成向量的形式为

那么可以求出该线性方程的解

4.2 非线性项处理

首先证明|u|2是常数.在方程(17)两端同时乘以,可得

然后取方程(17)的共轭后乘以u可得

将上述两式相加即可证得|u|2是一个常数,则非线性方程(17)可看作常系数常微分方程,解该常微分方程可得

将上述线性方程的解与非线性方程的解分别带入Strang分裂方法中,可以得到求解该方程的Strang分裂方法

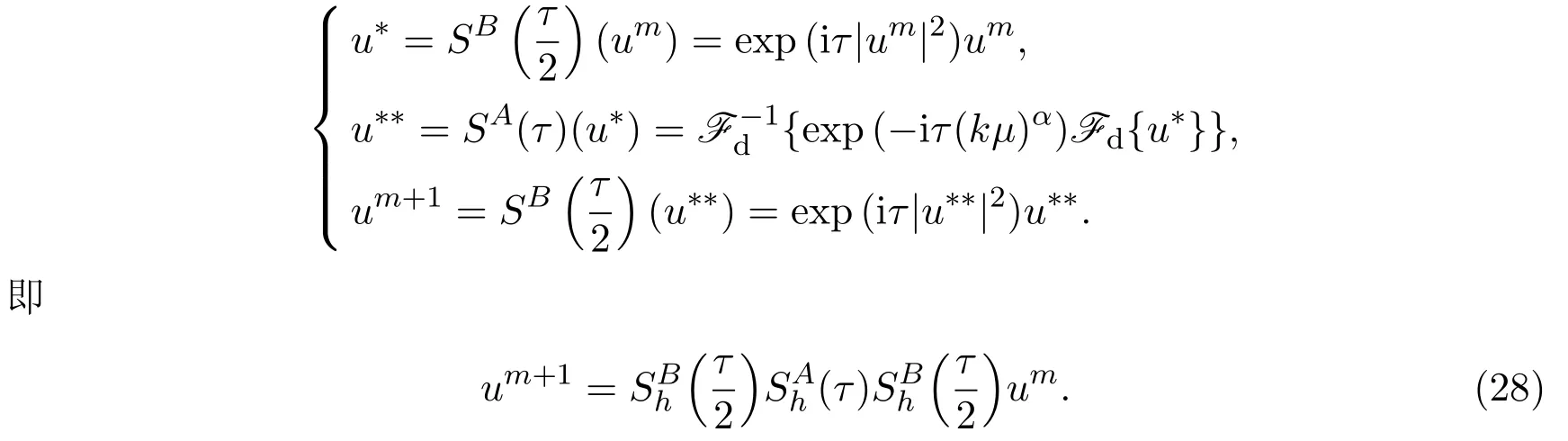
5 空间分数阶 Schrödinger方程的数值结果

根据上面的数值方法,取周期T=200,x=[−50,50],t=[0,10],N=1000.得出了初值(8a),(8b),(8c)分别取α=2,1.6,1.2时的数值结果.

图2|U|在初值(8a),α=2,1.6,1.2的俯视图

图3 初值(8a),α=2,1.6,1.2,在t=10的切面图

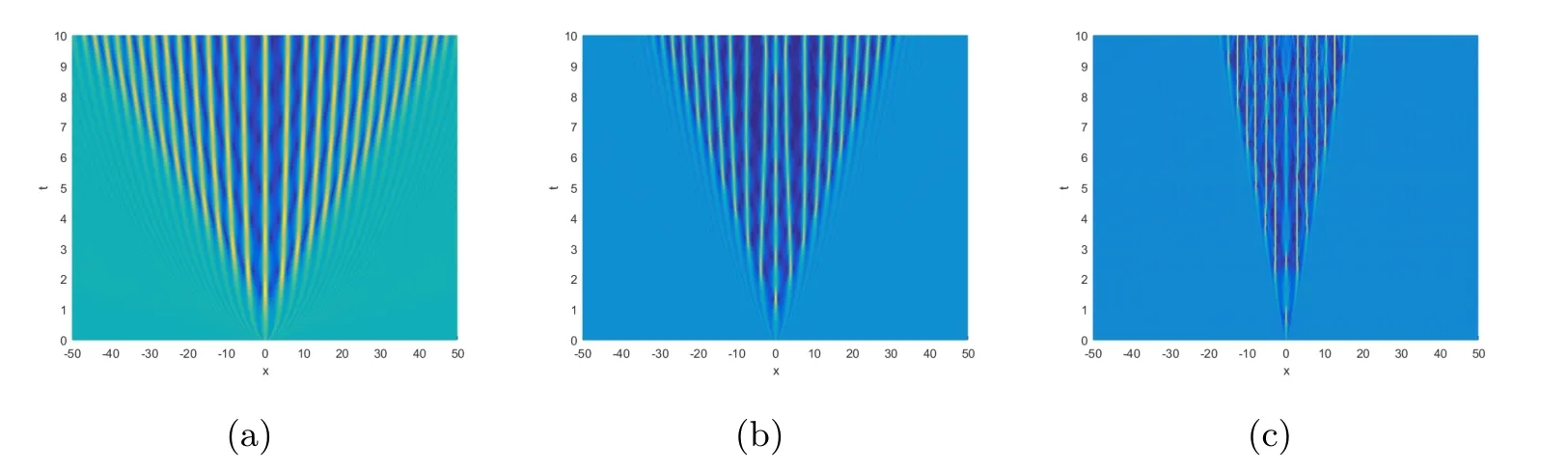
图4|U|在初值(8b),α=2,1.6,1.2的俯视图

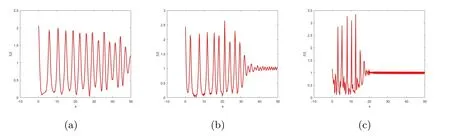
图5 初值(8b),α=2,1.6,1.2,在t=10的切面图

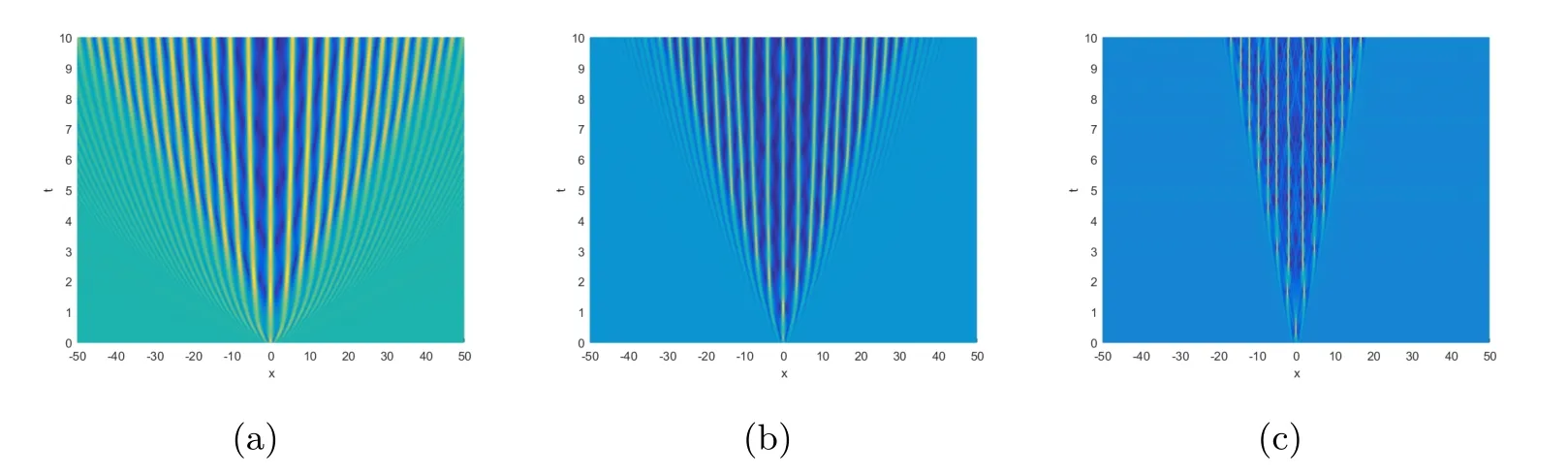
图6|U|在初值(8c),α=2,1.6,1.2的俯视图

图7 初值(8c),α=2,1.6,1.2,在t=10的切面图

图2,图 4,图 6是空间分数阶薛定谔方程在初值 (8a),(8b),(8c)时,α分别取2,1.6,1.2时的密度图像俯视图,当α=2时,为整数阶薛定谔方程.通过与整数阶薛定谔方程的比较,可以看出该方程在初值(8a),(8b),(8c)在不同α的取值下,图像仍是由中间的楔形区域和两边的扇形区域组成,可以看出楔形区域仍是振荡的,扇形区域仍是|U|=1的平面.三个图形整体变化趋势仍保持相似,但是随着α的值的变小,楔形区域的振荡宽度变小,峰值反而变大.图3,图5,图7表示该方程在初值(8a),(8b),(8c)时,α分别取2,1.6,1.2且t=10时刻的切面图像.从图中可以看出在t=10时刻,在不同α的取值下,该方程在初值(8a),(8b),(8c)的振荡区域和峰值,以及渐进结果.

由以上空间分数阶的数值结果可以看出,当从整数阶薛定谔方程变化为空间分数阶薛定谔方程时,图像仍然由两部分构成,中心仍未振荡的楔形区域,两边为两个扇形平面,但随着α变小中间楔形区域振荡范围变小.可以看出对于空间分数阶薛定谔方程来说,该不稳定性仍然不受初值的影响,即可说明这种调制不稳定性对于不同的背景下仍然保持相似的不稳定性结构.

6 结论

结合整数阶薛定谔方程的调制不稳定性[3]可知,从整数阶薛定谔方程在以上三个不同初值的数值结果可以看出相关散射问题的频谱都是连续的.并且其渐进行为,峰值,以及峰值的位置都是非常相似的.同样,空间分数阶薛定谔方程对于不同的初值,不同的α取值,数值结果的整体变化过程基本上保持不变.但随着α取值的变化,图像的峰值以及振荡范围发生了明显的变化.虽然从整数阶到分数阶的变化过程中,随着α的逐渐变小,图形的振荡区域变小,但整体的进化趋势仍然是相似的,这表明这种调制不稳定行为是一个通用的特性,即在不同物理背景下这种不稳定性是相似的.下一步,将进一步从数学上严格分析本文的发现,推导出不稳定区域和分数阶指标α之间的关系.