覆盖近似空间的连续与同胚映射
2019-07-05何家莉
何家莉
(玉林师范学院数学与统计学院,广西 玉林 537000)
1 预备知识
由于科技的不断进步,产生了大量不完备的信息系统.再用经典的数学理论处理不完备的信息系统变得极其困难.为了解决这一困难,文献[1]提出了模糊集理论.虽然该理论可以用来处理不确定性问题,但是该理论添加了人为的因素,会导致结果的不精确.文献[2]提出了粗糙集理论.该理论是一种处理不完备、不精确信息系统的强大工具,也是处理不确定知识的有效工具,因此该理论被成功地应用于许多领域.但是Pawlak粗糙集(也称经典粗糙集)是在等价关系的基础上定义上下近似算子,由于等价关系是很强的关系,因此有诸多局限.为了解除这种限制,文献[3]利用覆盖关系来代替等价关系,进而在1983年提出了覆盖粗糙集这一概念.随着对覆盖粗糙集研究的不断深入,获得了大量优秀结果.文献[4]利用协调映射研究了覆盖粗糙集的不变性,文献[5]利用拓扑的方法研究了覆盖广义近似空间.文献[6-7]研究了覆盖粗糙集的上近似算子成为拓扑闭包算子的充要条件以及对应的隶属度函数等问题.文献[8]研究了一般关系的粗糙集[8].文献[9-10]研究了覆盖近似空间的拓扑刻画及对应的公理化刻画等问题,文献[11]研究了覆盖近似空间的覆盖的约简等.基于以上讨论,为了更好地研究覆盖近似空间,本文将讨论覆盖近似空间的连续性和分离公理,进而在某种程度上提供覆盖近似空间的一种分类方法.为此,先介绍本文需要的基本概念.
定义 1.1[3]设U是任意一个论域以及C是论域U的一个不包含空集子集族.如果∪C=U,则称C是论域U的一个覆盖,称(U,C)是覆盖近似空间.
定义 1.2[9]设(U,C)是覆盖近似空间.对任意的x∈U以及任意的X∈P(U),定义如下:

引理1.1设X和Y是两个集合,f:X→Y是映射.则
(1)对任意的A⊆X,有A⊆f−1(f(A));
(2)对任意的B⊆Y,有f(f−1(B))⊆B,若f为满射,则有f(f−1(B))=B;
(3)对任意的A⊆X,B⊆Y,则f(A)⊆B当且仅当A⊆f−1(B).
2 覆盖粗糙连续映射与覆盖粗糙同胚
引理 2.1设(U,C)是覆盖近似空间,则对任意的X⊆U以及Xi⊆U(i∈I),有

证明(1)首先证明对任意的,由定义1.2可得到,进而可得到N(y),再由定义1.2可得到,从而有,因此

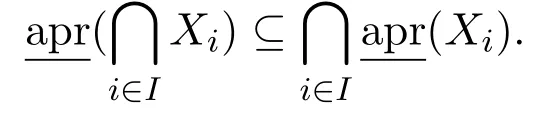
下面将证明反包含关系.
(3)用类似于(2)的证明方法,同理可证结论成立.


定义 2.1设(U1,C1)和(U2,C2)是两个覆盖近似空间,f:U1→U2是一个映射.若对任意的X⊆U1有,则称f为覆盖近似空间(U1,C1)到覆盖近似空间(U2,C2)的覆盖粗糙连续映射.若f是一个双射且f和f−1都是覆盖粗糙连续映射,则f称为覆盖近似空间(U1,C1)到(U2,C2)的覆盖粗糙同胚映射.其中f(X)={f(x):x∈X}.
命题 2.1设(U1,C1)和(U2,C2)是两个覆盖近似空间,f:U1→U2是映射.则下列四条结论等价:
(1)f是(U1,C1)到(U2,C2)的覆盖粗糙连续映射;
(2)对任意的Y⊆U2,有;
(3)对任意的Y⊆U2,有;
(4)对任意的x∈U1,有.
证明(1)⇔(2).设(1)成立,则对任意的Y⊆U2,由f是覆盖粗糙连续映射以及引理1.1(2)知.再由引理1.1(3)知

因此结论(2)成立;反之设(2)成立,对任意的X⊆U1,有

(2)⇔(3).设 (2)成立.对任意的Y⊆U2,由 (2)得又由引理2.1(1)及f−1保持补运算可知

(1)⇔(4).(1)⇒(4)显然成立.设 (4)成立,对任意的X⊆U1有由 (4)可知.再由引理2.1(4)及f保持并运算可知

综上所述(1)⇔(4).
定理 2.1设(U1,C1),(U2,C2)和(U3,C3)是覆盖近似空间.若
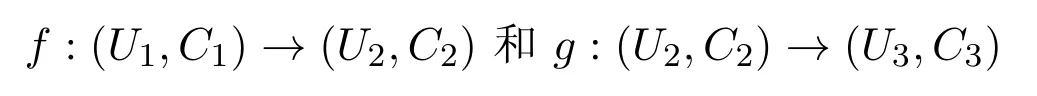
都是覆盖粗糙连续映射,则g◦f:(U1,C1)→(U3,C3)也是覆盖粗糙连续映射.
证明由f是覆盖粗糙连续映射可知对任意的X⊆U1,有又由于f(X)⊆U2以及g是覆盖粗糙连续映射知.从而.即.故g◦f也是覆盖粗糙连续映射.
由定义2.1,命题2.1以及定理2.1容易得到下面的定理:
定理 2.2设(U1,C1)和(U2,C2)是两个覆盖近似空间,f:U1→U2是双射.则下列四条结论等价:
(1)f是(U1,C1)到(U2,C2)的覆盖粗糙同胚映射;
(2)对任意的X⊆U1,有
(3)对任意的Y⊆U2,有
(4)对任意的Y⊆U2,有
定理 2.3设(U1,C1),(U2,C2)和(U3,C3)是覆盖近似空间,则有:
(1)恒等映射i:(U1,C1)→(U1,C1)是覆盖粗糙同胚映射;
(2)如果f:(U1,C1)→(U2,C2)是覆盖粗糙同胚映射,则f−1:(U2,C2)→(U1,C1)也是覆盖粗糙同胚映射;
(3)若f:(U1,C1)→(U2,C2)和g:(U2,C2)→(U3,C3)都是覆盖粗糙同胚映射,则g◦f:(U1,C1)→(U3,C3)也是覆盖粗糙同胚映射.
定义 2.2对覆盖近似空间(U,C)中的任意一个点x,若则称覆盖近似空间(U,C)满足T1分离性,也称(U,C)为T1空间.
例2.1存在满足T1分离性的覆盖近似空间.
设U是任意一个论域,C=P(U){∅}.由定义2.2,容易验证覆盖近似空间(U,C)满足T1分离性.
例2.2存在不满足T1分离性的覆盖近似空间.
设U是任意一个论域,取C={U}.由定义2.2,容易验证(U,C)不满足T1分离性.设(U,C)是任意一个覆盖近似空间,以C为闭子基诱导的拓扑记作τC.拓扑空间(U,τC)称为覆盖近似空间(U,C)诱导的拓扑空间.
引理 2.2拓扑空间(U,τ)是拓扑T1空间当且仅当U中的每一个单点集是闭集.
定理 2.4设(U,C)是覆盖近似空间且(U,τC)是由(U,C)诱导的拓扑空间.则覆盖近似空间(U,C)是T1空间当且仅当(U,τC)是T1拓扑空间.
证明⇒设覆盖近似空间(U,C)是T1空间,则对任意的x∈U有{x}=N(x).否则,存在a∈N(x),由定义 1.2知,这与矛盾.下面证为闭集.,由引理 2.2知 (U,τC)是拓扑T1空间.
⇐设(U,τC)是拓扑T1空间.则对任意的x∈U,

又因为
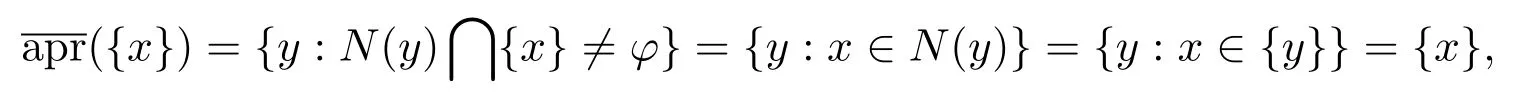
因此(U,C)是T1空间.
定理 2.5设(U1,C1),(U2,C2)是两个覆盖近似空间且f是覆盖近似空间(U1,C1)到覆盖近似空间(U2,C2)的覆盖粗糙同胚映射,则覆盖近似空间(U1,C1)是T1空间当且仅当覆盖近似空间(U2,C2)是T1空间.
证明⇒设覆盖近似空间(U1,C1)是T1空间且f是覆盖近似空间(U1,C1)到覆盖近似空间(U2,C2)的覆盖粗糙同胚映射.则对任意的y∈U2,存在唯一的x∈U1使得x=f−1(y).又因为覆盖近似空间(U1,C1)是T1空间,所以
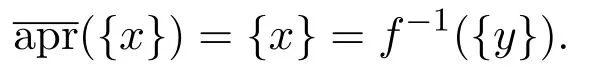
⇐采用上面类似的方法可以证明当覆盖近似空间(U2,C2)是T1空间时,覆盖近似空间(U1,C1)也是T1空间.
