四元数矩阵的新特征值定位

尹彩霞,李朝迁

(云南大学数学与统计学院,云南 昆明 650500)

1 引言

1843年,爱尔兰数学家Hamilton在寻找将复数扩展到更高空间维度的方法时引入了四元数.如今,四元数和四元数矩阵[1]在狭义相对论和非相对论[2-3]、群表示[4-6]、电弱模型[7]、信号处理[8-9]、计算机视觉[10]和量子物理学[11]等有广泛应用.随着上述学科的迅速发展,对四元数和四元数矩阵的理论性质[12]和数值计算进行深入研究越来越有必要.然而,四元数对于乘法的非交换性使得对四元数矩阵的研究通常是困难的,也使得四元数矩阵的特征值[13]比常规矩阵复杂.精确计算其特征值非常困难,为此一些学者转而对其定位或估计,最早的结果为文献[14]提出的Geršchgorin圆盘定理.接着,文献[15]提出了Brauer卵型定理,改进了上述结果.本文将对四元数矩阵进一步研究,得到新的特征值包含集,并证明所得结果优于文献[14-15]的结果.

为了研究方便,引入如下记号.R表示实数的全体,C表示复数的全体.H表示四元数的全体:H={a=a0+a1i+a2j+a3k,a0,a1,a2,a3∈R},其中i,j,k满足

对于a=a0+a1i+a2j+a3k∈H,a的共轭为=a0−a1i−a2j−a3k,a的模为.下面给出四元数矩阵的定义及其性质.

定义 1.1[16]设矩阵A=(aij)m×n,若aij∈H,则称A为四元数矩阵,记为A∈Hm×n.

当n=1时,X∈Hm×1为四元数列向量,X的转置记为XT.

定义 1.2[1]设A∈Hn×n,若存在λ ∈H 及X=(x1,x2,···,xn)T∈Hn×1,X0,使得AX=λX,则称λ为A的左特征值,记σl(A)={λ ∈H|AX=λX}.

定义 1.3[1]设A∈Hn×n,若存在λ ∈H及Y=(y1,y2,···,yn)T∈Hn×1,Y0,使得AY=Y λ,则称λ为A的右特征值,记σr(A)={λ ∈H|AY=Y λ}.

定理 1.1[15]对于任意四元数序列x1,x2,···,xn∈H,有下述不等式成立:

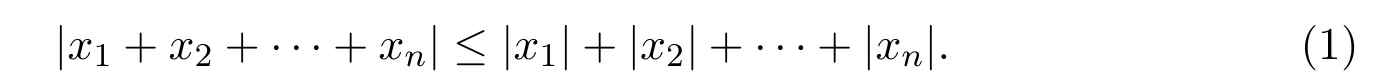
文献[12]提出:四元数矩阵A奇异(不可逆)当且仅当0是A的一个(左或右)特征值.其次,如果A是严格行或列对角占优四元数矩阵,则A可逆.同时也给出了四元数矩阵的左特征值包含集,即Geršchgorin圆盘定理.

定理 1.2[14](四元数矩阵 Geršchgorin圆盘定理)设A=[aij]∈Hn×n,λ为A的左特征值,则

在定理1.2的基础上,文献[15]给出了优于Geršchgorin圆盘定理的四元数矩阵左特征值包含集,即Brauer卵型定理.

定理 1.3[15](四元数矩阵Brauer卵型定理)设A=[aij]∈Hn×n,λ为A的左特征值,则

2 主要结果

利用四元数矩阵[17]的性质,得到四元数矩阵非奇异性的判定条件.

定理 2.1设A=[aij]∈Hn×n,n≥2,若存在j∈N,对于任意的,i∈N,使

则A非奇异.

证明由 (4)式得,存在j0∈N,对于任意的0,i∈N,存在γ>0,使得

则矩阵AD:=[αij]∈Hn×n,其中

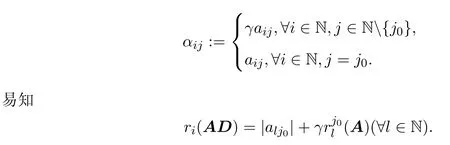
由(8)式知,AD是严格对角占优四元数矩阵,则AD非奇异.又因D非奇异,故A非奇异.证毕.

由上述四元数矩阵A的非奇异性判定条件,得出四元数矩阵A的左特征值包含区域.

定理 2.2设A=[aij]∈Hn×n,n≥2,则

其中,

证明假设结论不成立,则存在λ∈σl(A),使得(A),即存在j∈N,对于任意的,i∈N,都有

由定理2.1得,矩阵λI−A是非奇异的.但λ是A的左特征值.故,|λI−A|=0,这与矩阵|λI−A|非奇异矛盾,因此假设不成立.所以σl(A)⊆D(A).证毕.

下面,将定理2.2中新特征值包含集分别与定理1.3和定理1.4中的结果进行比较.

定理2.3设A=[aij]∈Hn×n,n≥2,D(A)⊆Γ(A).

证明令z∈D(A),由定理 2.2得,对于任意的j∈N,存在,i∈N,使

得z∈Vij(A),即

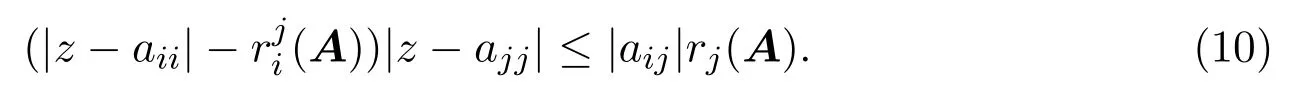
如果Γ(A),对于任意的k∈N,有|z−akk|>rk(A),因此,

这与(10)式矛盾.故对任意的z∈D(A),有z∈Γ(A).所以,D(A)⊆Γ(A).证毕.

定理 2.4设A=[aij]∈Hn×n,n≥2,D(A)⊆K(A).

证明令z∈D(A),由定理 2.2得,对于任意的j∈N,存在i∈N(),有

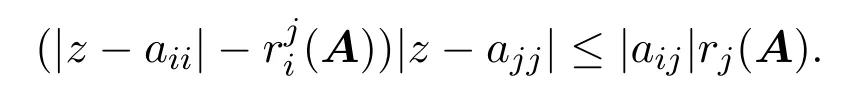
由定理 2.3知D(A)⊆Γ(A),则存在q∈N,使得|z−aqq|≤rq(A).对于q,存在p∈N(),使得z∈Vpq(A),即 (|z−app|−rqp(A))|z−aqq|≤|apq|rq(A).易得

即|z−app||z−aqq|≤rp(A)rq(A).因此,z∈K(A).故D⊆K(A).证毕.

例 2.1考虑四元数矩阵

由定理1.3和定理2.2得σl(A)⊆K(A)={z∈H:|z−3||z−4|≤12},

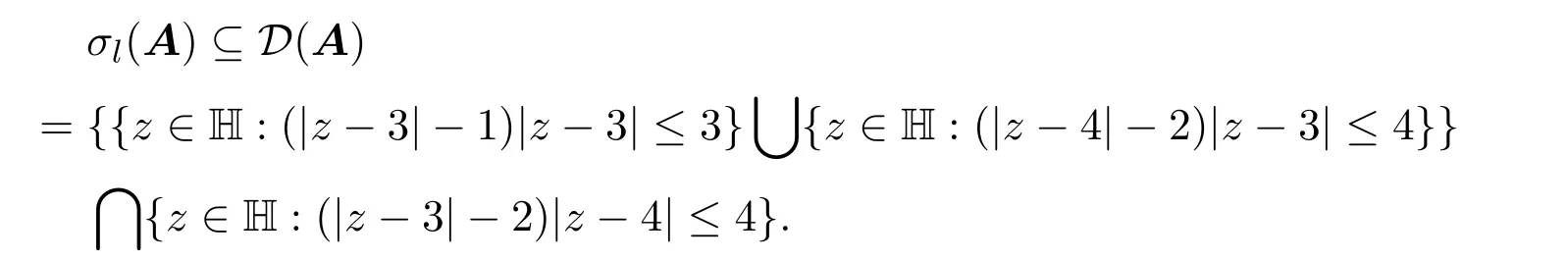
通过不等式放缩易得,D⊆K(A),并且0∈K(A),0(A),D(A)K(A).因此,定理2.2的结果优于定理1.3的结果,即定理2.2中四元数矩阵左特征值包含集比已有结果好.

上述是对四元数矩阵左特征值的定位,下面考虑四元数矩阵的右特征值包含区域.由于四元数乘法的不可交换性,故定理2.2的证明方法不适用.因此,需利用不同的方法得到一类特殊四元数矩阵右特征值定位结果.

定理 2.5设A=[aij]∈Hn×n,n≥2且aii∈R,则σr(A)⊆D(A).

证明令λ ∈σr(A),且 0=(x1,x2,···,xn)T∈Hn×1是对应的特征向量.对于任意的j∈N,令

取τ∈H,使得xpλ=τxp,由AX=Xλ的第p个等式且aii∈R有

对上式取模有

同时,取γ∈H,使得xjλ=γxj,由AX=Xλ的第j个等式且ajj∈R有

若|xj|=0或|xp|=0,结论成立.否则,由(12)式和(14)式得

故λ∈Vpj(A).因此,λ∈D(A).证毕.

注2.1定理2.2和定理2.5的区别在于条件中有无aii∈R,若将定理2.5中aii∈R去掉,(11)式和(13)式不一定成立,无法得到此结论.

注 2.2由定理2.4知,该定理结果改进了文献[18]中的结果.

3 总结

本文给出了四元数矩阵新的特征值包含集,将其与Geršchgorin圆盘定理和Brauer卵型定理给出的左特征值包含集进行了比较,给出了理论证明,并用实例具体说明了本文定理所得的左特征值包含集更优于Geršchgorin圆盘定理和Brauer卵型定理给出的结果.同时,也得到了四元数矩阵的右特征值包含集.接下来,在已有四元数矩阵特征值包含集的基础上,如何给出更有效的包含集是值得研究的.