二次截面Nakayama代数的McCoy性

周玉业,程智

(安徽师范大学数学与统计学院,安徽 芜湖 241003)

1 引言

在本文中,R是一个有单位元的环,R上的多项式环记作R[x],R上的n阶矩阵环记作Mn(R).K是一个域,A为域K上的有限维代数.

文献[1]指出所有的交换环都是McCoy环.后来,文献[2-3]引入McCoy环的定义:如果对于任意的多项式f(x),g(x)∈R[x]{0},有f(x)g(x)=0,则存在r∈R{0},使得f(x)r=0(或rg(x)=0),那么环R称为右 McCoy(或左McCoy)环.若一个环既是左McCoy环,又是右McCoy环,则该环称为Mc-Coy环.McCoy环上的矩阵环未必是McCoy环.但是McCoy环上一些特殊形式的矩阵环仍然是McCoy环,而且两者之间的McCoy性是等价的[4].考察哪些环类是McCoy环一直是大家关心的问题.文献[5]提出了三个公开问题,其中有两个问题都是考察某些环类是否是McCoy环.部分学者则是从McCoy环不同形式的扩张来构造新的McCoy环类[6-8].

本文将考虑二次截面Nakayama代数中的所有McCoy环.为方便起见,约定代数A是不可分解的,即A不可以写成两个代数的直积.记代数A的Jacobson根为radA,如果A/radA同构于有限个域K的直积,则代数A称为基本(basic)的.一个熟知的结论是所有的有限维基本代数都同构于路代数KQ的商代数.这里Q=(Q0,Q1)是一个quiver,其中点的集合Q0以及箭向的集合Q1都是有限集.路代数KQ中的基是Q中的道路,乘法由道路连接给出.设I为A中所有箭向生成的理想,代数A=KQ/I2称为二次截面Nakayama代数,其中Q是An型(即由n个点以及n−1个箭向组成的树),或者是n-圈(即由n个点和n个箭向组成的圈).Nakayama代数A是自内射的充要条件是Q是一个n-圈.

Nakayama代数是一类常见的表示有限代数,这类代数一直是代数学者的研究热点.例如文献[9]就对Nakayama代数上的所有Gorenstein投射模进行分类,文献[10]则考虑了Nakayama代数上的一些同调性质.本文主要给出以下结果.

定理 1.1二次截面Nakayama代数A是McCoy环的充要条件是A是自内射代数.

2 引理

首先给出更一般的结论并加以证明.设

记V2n(R)是形如 Diag(U1,U2,···,Un)的对角分块矩阵集合.不难证明,V2n(R)是M2n(R)的子环.

引理 2.1设R是有单位元的环,则R是右(或左)McCoy环当且仅当V2n(R)是右 (或左)McCoy环.

证明这里V2n(R)是M2n(R)的子环.我们直接验证R是右McCoy环的情况,R是左McCoy环的证明方法类似.

(必要性)这里将V2n(R)中第i行,第j列元素为1,其余位置元素全部为0的2n阶矩阵记作ei,j.为方便起见,也记ei,i为ei.设

是V2n(R)[x]中的非零多项式,且满足F(x)G(x)=0,其中

是V2n(R)中的矩阵.其中aki,bkj,cli,dlj是R中的元素,

其中整数s,t,k,l=1,2,···,n.那么有

若有某个fs(x)=0.则存在S=e2s−1,2s,使得F(x)S=0.于是设fs(x)0,其中s=1,2,···,n.

情形 1gt(x)0,其中t是 1,2,···,n中的某个整数.

由F(x)G(x)=0,知ft(x)gt(x)(e2t−2+e2t−1)=0,则ft(x)gt(x)=0.这说明存在非零的rt∈R,使得ft(x)rt=0.因此F(x)rte2t−1,2t=0.

情形 2gt(x)=0,其中t是 1,2,···,n中的任意整数.

因为

所以必有某个ql(x)0.根据F(x)G(x)=0以及V2n(R)的结构,可得到

因而fl(x)ql(x)=0.这说明存在非零的rl∈R,使得fl(x)rl=0,因此

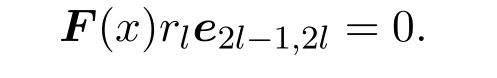
因此,V2n(R)是右McCoy环.

(充分性)设

是R[x]中的两个非零多项式,且满足f(x)g(x)=0.记

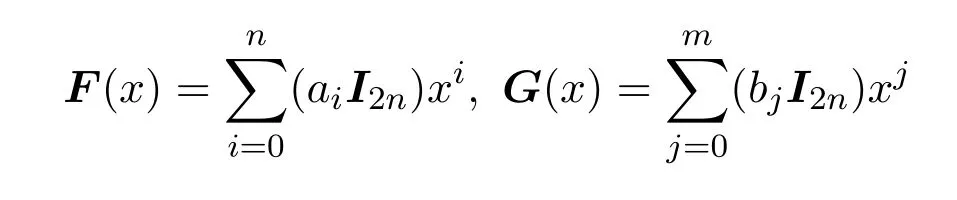
是V2n(R)[x]中的多项式,其中I2n是V2n(R)中的单位矩阵.因为f(x)0,g(x)0,所以F(x),G(x)都是非零多项式.又因为f(x)g(x)=0,所以

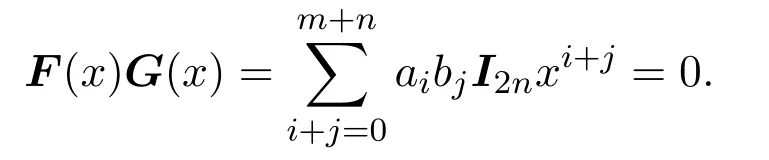
于是,V2n(R)是McCoy环说明了存在非零矩阵

使得F(x)S=0,其中k,l=1,2,···,n是R中元素.若存在某个si0,则f(x)si=0.否则,由于0,则存在某个tj0,使得f(x)tj=0.因此,R是右 McCoy环.

若R是一个域,考虑以下的矩阵集合Tn+1(R).令

并记J为Tn+1(R)的Jacobson根,则有下面的结论.

引理 2.2环V2n(R)和Tn+1(R)/J2是同构的.

证明记ei,j是2n阶矩阵V2n(R)中第i行,第j列元素是1,其余元素是0的矩阵.类似地,为方便起见,我们也将ei,i,Ei,i分别记为ei,Ei.

注意到V2n(R)中的所有矩阵可表达为如下形式:

Tn+1(R)/J2中的所有矩阵可表达为如下形式:

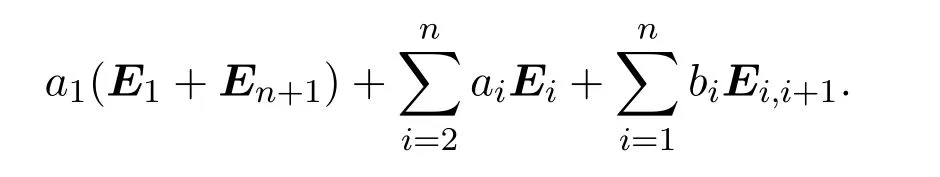
其中ai,bj∈R,i,j=1,2,···,n.

构造映射f:V2n(R)→Tn+1(R)/J2;x 7−→y.显然,f是双射.且对V2n(R)中的任意矩阵x,x′,可以直接证明f(x+x′)=f(x)+f(x′),f(xx′)=f(x)f(x′).因此f是环V2n(R)和Tn+1(R)/J2之间的一个同构.

3 定理证明

先证该定理的充分性:

注意到域 K是交换环,从而是 McCoy环.下面证明环Tn+1(K)/J2KQ/I2,Q是n个点的圈,I是由所有箭向生成的理想.记Q={Q0,Q1},Q0={1,2,···,n}是由n个点组成的集合,Q1={α1,···,αn−1,αn}是由所有箭向 (长度为1的道路)组成的集合,即对任意i=1,2,···,n−1,αi:i→i+1以及αn:n→1为Q中的所有箭向.注意到代数KQ/I2中的所有道路恰是长度为0的道路ωi,i∈Q0,以及Q1中的所有道路全体.于是KQ/I2中的元素x可表达为如下形式:

代数Tn+1(K)/J2中的元素y可表达为如下形式:

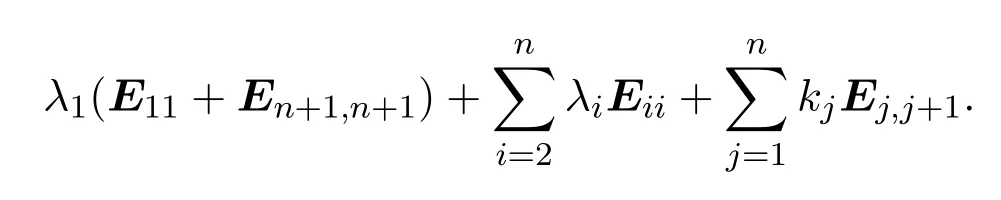
其中系数λ1,···,λn,k1,···,kn∈K.现构造g:KQ/I2−→Tn+1(K)/J2;.显然g是映射且是双射.

对于 KQ/I2中的任意元素x,x′,直接验证知g(x+x′)=g(x)+g(x′).

注意到对 [1,n]中的任意整数i,j,若i=j,则ωiωj=ωi;若,则ωiωj=0,以及ωiαi=αi=αiωi+1.并且在环Tn+1(K)/J2中,Ej,j+1Ej+1,j+2=0.于是

从而g是环KQ/I2到Tn+1(K)/J2的同构.

下证定理的必要性:

假设二次截面Nakayama代数A不是自内射的,则Q是An型的,即Q=(Q0,Q1),其中Q0={1,2,···,n},Q1={αi|αi:i→i+1,1≤i≤n−1}.

记B=KQ/I2,取B[x]中的两个非零多项式