Cahn-Hilliard方程的动态分歧

武瑞丽,柴容倩,钱小瑞

(四川大学锦城学院,四川 成都 611731)

1 引言

分歧问题是自然界中普遍存在的问题,它广泛存在于物理,化学和生物等学科中,分为定态分歧和动态分歧.近年来,在研究非线性演化方程的稳定性与分歧方面,马天和汪守宏创立了一套新的分歧理论与跃迁理论[1-2],本文就利用该理论讨论了Cahn-Hilliard方程的动态分歧.

本文考虑如下Cahn-Hilliard方程的初边值问题:

其中λ为参数,α1,α2>0为常数,Ω=[0,L]×[0,L],n为Ω边界处的法向量.Cahn-Hilliard方程被 Cahn和 Hilliard在文献 [3]中首先引入,用来描述包含两种物质的混合物 (比如合金,玻璃,聚合物等)在达到一种不稳定状态时所发生的相分离.近年来对Cahn-Hilliard方程的分歧研究有很多,如文献[4-5]研究了非自治反应扩散方程的拉回吸引子的存在性,文献[6]考虑了粘性Cahn-Hilliard方程的拉回D-吸引子存在性问题,文献 [7]研究了具有一般非线性项的Cahn-Hilliard方程的整体吸引子存在性,文献[8]重点分析了一类带Neumann边界条件的Cahn-Hilliard方程的定态分歧.本文继续了文献[8]的研究工作,运用文献 [1-2]中提出的分歧理论与跃迁理论对Cahn-Hilliard方程做了进一步的分析,讨论了Cahn-Hilliard方程的动态分歧结果,给出了其发生动态分歧的条件及临界点,并同时得到了在Neumann边界条件下,方程分歧出的稳定奇点吸引子和鞍点的表达式.

2 预备知识

在这一部分,首先将Cahn-Hilliard方程进行算子化处理,并详细计算出其特征值与特征向量,最后给出本文的主要工具―非线性方程的动态分歧理论[1-2].

2.1 方程的处理

建立空间如下:

定义如下算子:

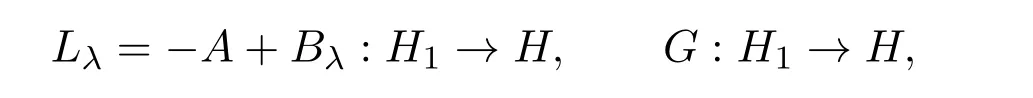
其中

则不难验证Lλ:H1→H是线性全连续场,方程(1)可转化为如下抽象形式

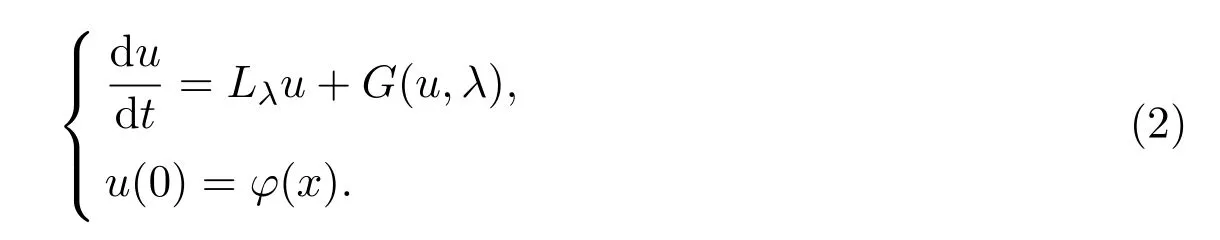
其中,Gλ满足Gλ:X1→X是一个连续算子,且Gλ(u)=o(|u|),这样方程就满足了线性全连续场谱理论的条件,因此可以运用该理论.

2.2 算子的特征值与特征向量

令ρk,ψk是下面Laplace算子的特征值和特征向量:

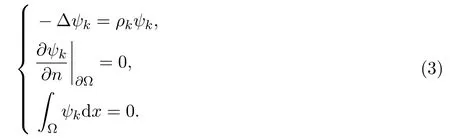
其中,ρk满足:0<ρ1=ρ2<ρ3<ρ4=ρ5<ρ6=ρ7<ρ8≤···,且

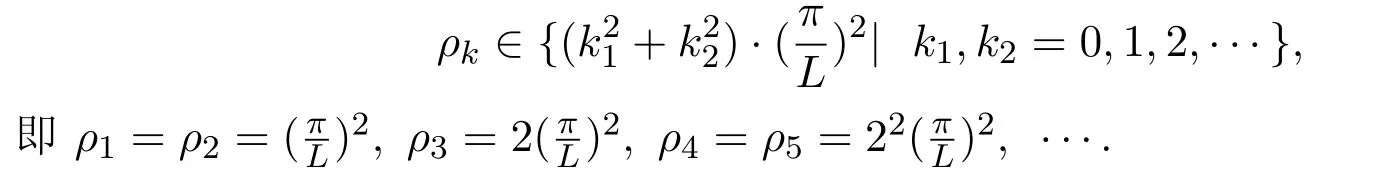
对应的特征向量:

其中k,n1,n2,n3,n4=1,2,···,即

设Lλ的特征值和特征向量分别为,经计算可得

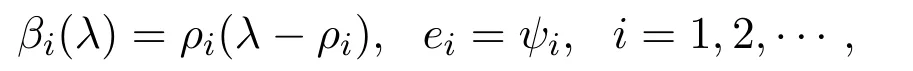
根据线性全连续场的谱理论,在λ=λ0的领域内有如下的空间分解:

其中E1=span{e1,e2},E2=span{e3,e4,e5,···},

2为E2在H中的闭包,对任意u∈H1,存在

使得u=u1+u2.

2.3 定义及引理

定义 2.1令uλ∈X1是方程 (1)在λ=λ0处的分歧解,若Lλ+G(·,λ)在uλ处的导算子Lλ+DuG(uλ,λ):X1→X,在λ0的充分小的领域内是线性同构的,则称该分歧解是正则的或非退化的.

引理 2.1每一个近似约化方程从λ=λ0处的非退化分歧解都唯一地对应于原方程从λ=λ0处的非退化的分歧解.

引理 2.2假设条件(4)-条件(5)成立,若G(u,λ)有展开式

其中,k≥0为一整数,Gk(u,λ)为k重线性算子,则方程(1)在λ=λ0附近的中心流形函数 Φ:E1→E2可表达为其中,P2:H→E2为规范投影,

3 主要定理及证明

定理 3.1在条件(4)-条件(5)下,方程(1)有如下结论成立:

(iv)分歧出的分歧解可表达为:

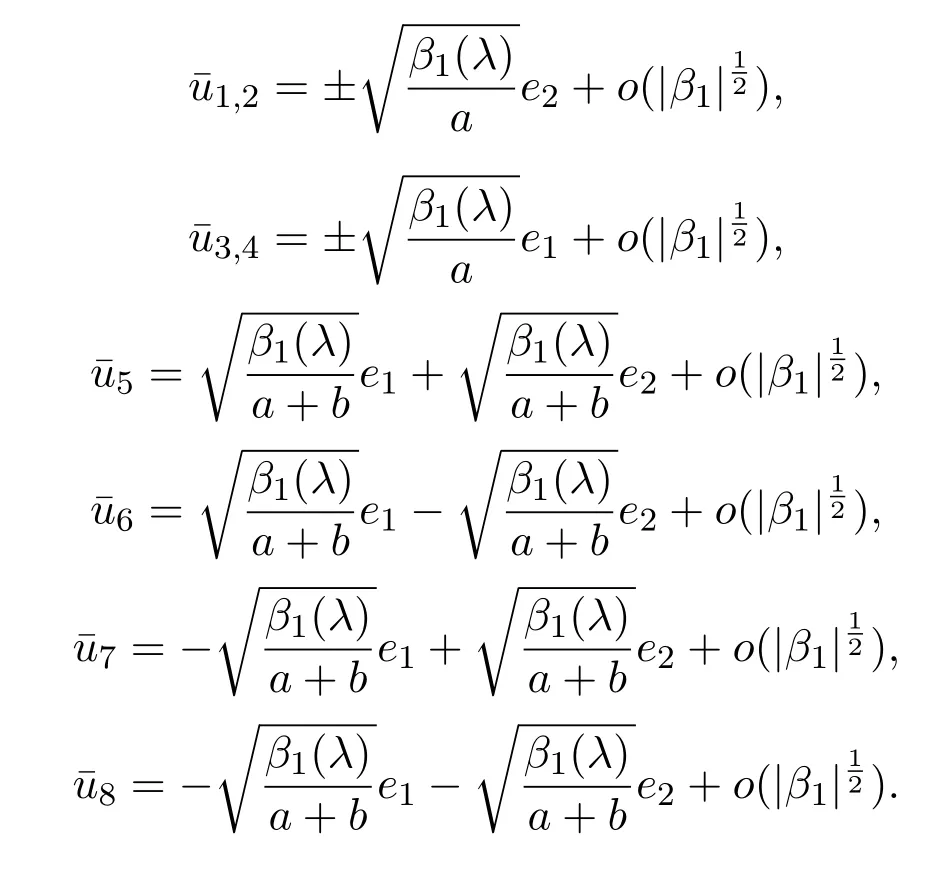
证明对方程 (1),由上一节的空间分解可知,∀u∈H1,有u=u1+u2.假设u=u1+Φ(u1,λ),其中Φ(u1,λ):E1→E2为中心流形函数.由 Lyapunov-Schmidt约化方法,知⟨ut,ei⟩=⟨Lλu,ei⟩+⟨G(u,λ),ei⟩,则方程 (1) 的分歧方程为:

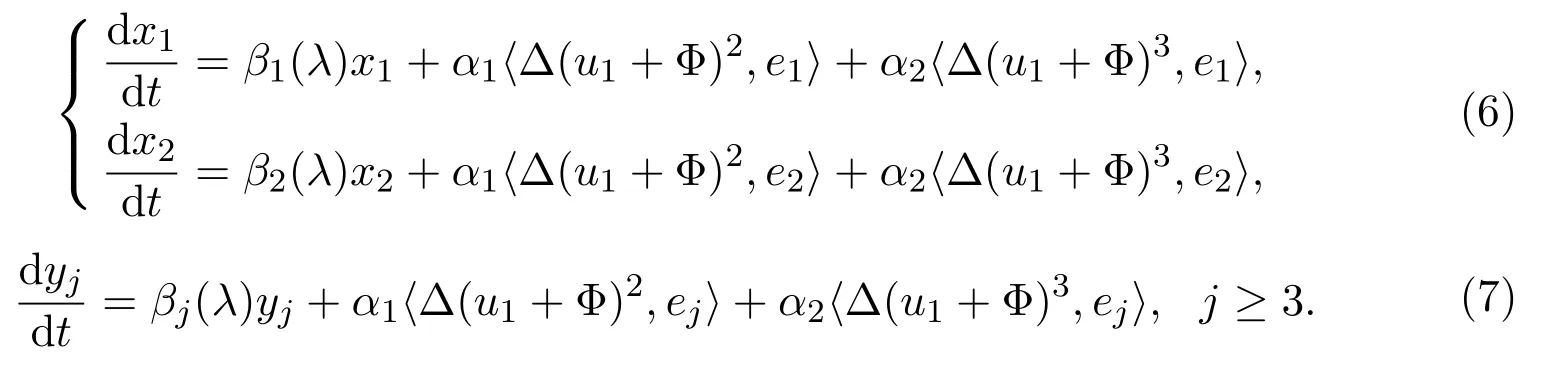
由计算可知

由此(8)式可化为

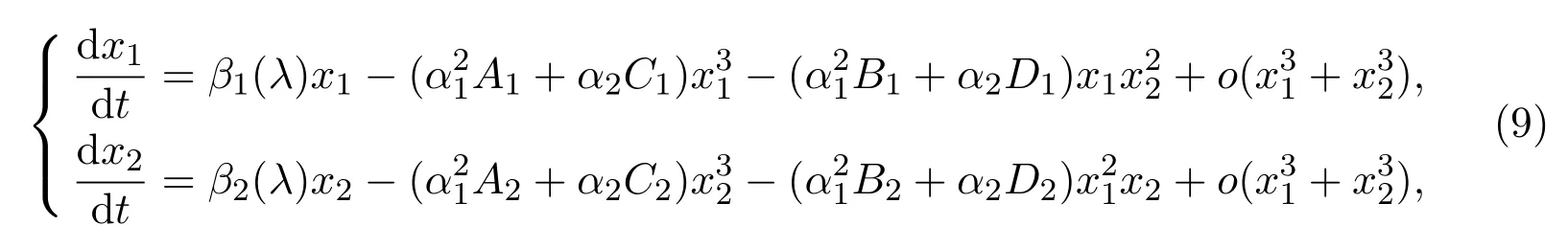
显然A1(λ)=A2(λ),B1(λ)=B2(λ),C1(λ)=C2(λ),D1(λ)=D2(λ).

可解出方程(10)的近似解有如下八个:

则方程(1)分歧出的分歧解为:

在λ0的充分小领域内,显然有: