The structure of Q-clean ring and its application

Sun Xiaoqing,Liu Xia,Hua Xiujuan

(School of Science,Xi′an University of Technology,Xi′an 710054,China)

Abstract：The notions of Q-clean elements in a ring and Q-clean ring are defined.Some basic properties of Q-clean rings are obtained.In particular,it is shown that every element in a Q-clean ring with 2 invertible is a sum of a quasi-invertible element and a square root of 1.Let Rbe a ring in which every element x∈R,x=xuxwhere u∈ .Then Ris Q-clean.Furthermore,we prove that the ideals of a Q-clean ring are also Q-clean.

Keywords：quasi-invertible,Q-clean ring,ideal

1 Introduction

Following Nicholson a ringRwith identity is called clean if every element ofRcan be written as the sum of an idempotent and a unit inR.A ring with central idempotents is clean if and only if it is exchange[1].Many authors investigated exchange rings and clean rings in references[1-4].Letdenotes the quasi-invertible elements,that is,

The definition of quasi-invertible element was used by Ara to study purely infinite ring as an infinite analogue of rings of stable rank one in references[5-6].We call a ringRis Q-clean if every element ofRcan be written as the sum of an idempotent and a quasi-invertible element inR.Clean rings are Q-clean by.Some basic properties of Q-clean rings are obtained in section 2.It is shown that every element in a Q-clean ring with 2 invertible is a sum of a quasi-invertible element and a square root of 1.And letRbe a ring in which every elementx∈R,x=xuxwhereu.ThenRis Q-clean.

In section 3,in order to study the ideal of Q-clean ring,the definition of Q-clean on rings without identity is given.According to this,it is shown that the ideal of a Q-clean ring(unitial or not)is also Q-clean.

Throughout this paper,Rdenotes an associative ring with identity.We denote byU(R),Id(R)andJ(R)the set of all units ofR,the set of all idempotents inR,and the Jacobson radical,respectively.

2 Q-clean rings

Let us start by recalling the concept of quasi-invertibility.We say that elementsxandyin a unital ringRare centrally orthogonal provided thatxRy=yRx=0,and we writex⊥y.An elementuin an arbitrary ringRis said to be quasi-invertible if there exist elementsa,binRsuch that

The set of quasi-invertible elements inRwill be denoted by

Ifu∈,then we have the equation(1−ua)u(1−bu)=0.Takingv=a+b−aubthis implies thatu=uvu.By computation

we have the relation(1−uv)⊥(1−vu).We say in this situation thatvis a quasi-inverse foru.

An elementxof a ringRis clean in[1]if it can be written as the sum of a unit and an idempotent inR.A ring is called a clean ring if every element ofRis clean.Many authors extend it in references[7-11].In this paper,we will extend it to a large class of rings,Q-clean rings.

Definition 2.1An elementrof a ringRis called Q-clean if there existe∈Id(R)andu∈such thatr=e+u.The ringRis called Q-clean if every element ofRis Q-clean.

The class of Q-clean ring is very large.For example,clean rings,one-sided unitregular rings,and regular QB-rings.Since,we have ifais Q-clean,then so is 1−a.IfRis commutative,then.Thus Q-clean commutative rings are clean rings.LetRbe a QB-ring and have stable range one.ThenRis Q-clean precisely that it is clean.

Now,we give some basic properties of Q-clean rings.

Lemma 2.1[5]IfIis an ideal in a unital ringRand∏:R→R/Idenotes the quotient morphism,then

Theorem 2.1The following hold:

(1)Every homomorphic image of a Q-clean ring is Q-clean;

Proof(1)It is straightforward from Lemma 2.1.

(2)Suppose that eachRiis a Q-clean ring.Letx=(xi)∈∏Ri.For eachi,writexi=ei+uiwhereei∈Id(Ri)and.Thenand.Hencex=e+uis a Q-clean expression ofx.Thereforea Q-clean ring.

The converse part is obvious from(1).This,we complete the proof.

LetS(R)be the nonempty set of all proper ideals ofRgenerated by central idempotents.An idealP∈S(R)is called a Pierce ideal ofRifPis a maximal(with respect to inclusion)element of the setS(R).IfPis a Pierce ideal ofR,then the factor ringR/Pis called a Pierce stalk ofR.The following result shows that the Q-clean property needs to be checked only for indecomposable rings or Pierce stalks.

Theorem 2.2LetRbe a ring.Then the following are equivalent:

(1)Ris Q-clean;(2)Every factor ring ofRis Q-clean;(3)Every indecomposable factor ring ofRis Q-clean;(4)Every Pierce stalk ofRis Q-clean.

Proof(1)⇒(2),(2)⇒(3)and(2)⇒(4)are directly verified.

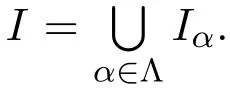
(4)⇒(1)LetMbe the set of all proper idealsIofRsuch thatIis generated by central idempotents and the ringR/Iis not Q-clean.Suppose thatRis not Q-clean.Then 0∈Mand the setMis not empty.It is directly verified as above that the union of every ascending chain of ideals fromMbelongs toM.By Zorn′s Lemma,the setMcontains a maximal elementP.By(4),it is sufficient to prove thatPis a Pierce ideal.Assume the contrary.By the definition of the Pierce ideal,there is a central idempotenteofRsuch thatP+eRandP+(1−e)Rare proper ideals ofRwhich properly contain the idealP.Since idealsP+eRandP+(1−e)Rdo not belong toMand are generated by central idempotents,R/(P+eR)andR/(P+(1−e)R)are Q-clean.Note that(R/(P+eR))×(R/(P+(1−e)R)).It follows from Theorem 2.1(2)thatR/Pis Q-clean,a contradiction.HencePis a Pierce ideal ofR,a contradiction.This,we complete the proof.

Theorem 2.3Ifxis Q-clean in R,so thatx=e+uwheree2=e∈Randu∈with quasi-inversev∈R,then each element of the formx+a(1−vu)+(1−uv)bwitha,b∈Rwill be Q-clean inR.

ProofLetu′=u+a(1−vu)+(1−uv)b.Evidently eachu′inRof the prescribed form equation(2.1)will be a partial inverse forv.Moreover,

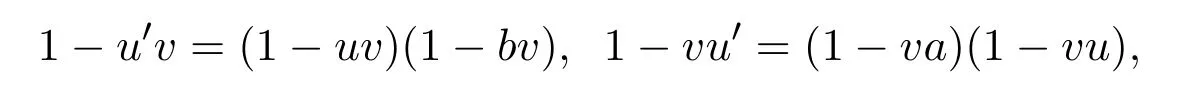
whence(1−u′v)⊥(1−vu′),so thatu′∈andu′is a quasi-inverse foru.Sincex+a(1−vu)+(1−uv)b=e+u+a(1−vu)+(1−uv)b,it is Q-clean inR.This,we complete the proof.

LetRbe a ring in which 2 is invertible.Camillo and Yu in reference[11]showed thatRis clean if and only if every element ofRis a sum of a unit and a square root of 1.We now take a look at the case for Q-clean rings.IfGis a group,we denote the group ring overRbyRG.It seems to be difficult to characterizeRandGfor whichRGis Q-clean in general.We here also focus onRwith 2∈U(R).This,we complete the proof.

Theorem 2.4LetRbe a ring in which 2 is invertible andG={1,g}be a group.

(1)Ris Q-clean if and only if every element ofRis a sum of a quasi-invertible element and a square root of 1;(2)RGis Q-clean if and only ifRis Q-clean.

Proof(1)SupposeRis Q-clean andx∈R,thenwheree2=eandu∈.Thusx=(2e−1)+2u,with(2e−1)2=1.It is easy to check that.Then 2u∈.

Conversely,ifx∈R,then 2x−1=f+uwheref2=1 andu∈.Thus.We have.Hencexis Q-clean,which shows thatRis a Q-clean ring.

(2)As an image ofRG,Ris Q-clean whenRGis Q-clean.

Conversely,Since 2∈U(R),we havevia the mapping

HenceRGis Q-clean by Theorem 2.1.This,we complete the proof.

Reference[12]proved that every element in a unit-regular ring is the sum of an idempotent and a unit.Reference[2]proved that every element in a one-sided unitregular ring is the sum of an idempotent and a one-sided unit.We get the similar result on Q-clean rings.

Lemma 2.2[5]IfRis a untial exchange ring the following conditions are equivalent:(1)Ris aQB-ring;(2)Every regular element inRextends to an element in;(3)For every regular elementxinRthere is avinsuch thatx=xvx.

Theorem 2.5LetRbe a ring.If for every elementxinRthere is auinsuch thatx=xux,thenRis a Q-clean ring.

ProofIt follows from Lemma 2.2 thatRis a regularQB-ring.By Theorem 5 in reference[3],for anya∈R,there exist an idempotente∈Rand au∈such thata=e+u.

3 Ideals

LetIbe a not necessarily unital ring.There is a canonical unitization=I⊕Z,with the obvious multiplication(a,n)(b,m)=(ab+ma+nb,nm)fora,binIandn,min Z.EvidentlycontainsIas an ideal with/I=Z.We write

Heres⊥tinImeans thatst=0 andts=0.We say in this case thatsandtare centrally orthogonal.

Lemma 3.1LetSbe any unital ring containingIas a subring,and letRdenote the unital subring ofSgenerated byIand 1.Then we have the equalities.

ProofStraightforward computations based on the equation

This,we complete the proof.

Corollary 3.1Ifx∈we can find a single elementyinRsuch that−(x+y+xy)and−(x+y+yx)are centrally orthogonal idempotents inR.

ProofCombine Proposition 2.2 in reference[6]and Lemma 3.1.

Lemma 3.2IfIis an ideal in a unital ringR,andt∈I,thent∈if and only if 1+t∈.

ProofIft∈,then by Corollary 3.1 we can find centrally orthogonal idempotents inIof the formp=−(t+s+ts)andq=−(t+s+st)for somesinI.SinceIis an ideal inRthis implies thatpRq=p2Rq2⊂pIq=0.SimilarlyqRp=0.It follows that 1+t∈with quasi-inverse 1+s.

Conversely,if 1+t∈we can find a quasi-inverse inR,written in the form 1+s,such that(1−(1+t)(1+s))⊥(1−(1+s)(1+t)).The equation 1+t=(1+t)(1+s)(1+t)shows thats=−t−t2−ts−st−tst∈I,whencet∈.

Note thatJ(I)⊆.IfRhas a unity,then;in factviax 7→1+x.Recall thatRis Q-clean if every elementa∈Rcan be written asa=e+uwheree2=e∈Randu∈.This,we complete the proof.

Theorem 3.1The following are equivalent for a ringR:

(1)Ris Q-clean;(2)For eacha∈R,a=e+xwheree2=eandx∈.

ProofLeta∈R.IfRis Q-clean,writea+1=e+uwheree2=eandu∈.Thena=e+xwherex=u−1∈by Lemma 3.2.

Conversely,ifa−1=e+xwheree2=eandx∈,thena=e+uwhereu=x+1∈by Lemma 3.2.

With this in mind,an elementainI(unitial or not)is called a Q-clean element ifa=e+xwheree∈Id(I)andx∈,andIis called a Q-clean ring if every element is Q-clean.Clearly,every homomorphic image of a Q-clean ring(unitial or not)is Q-clean,and the direct productof rings(unitial or not)is Q-clean if and only if eachIjis Q-clean.This,we complete the proof.

Lemma 3.3The following are equivalent forI:

(1)Iis Q-clean;

(2)WheneverI▹RwhereRis a ring,eacha∈Iis a Q-clean element ofR;

(3)(a,0)is Q-clean infor everya∈I.

Proof(1)⇒(2).Givena∈I▹R,let−a=e+xwheree2=eandx∈Thena=(1−e)+(−1−x)where(1−e)2=1−e.It follows from Lemma 3.2 that 1+x∈.Then−1−x∈.

(2)⇒(3).It is clear that takeR=.

(3)⇒(1).It is easy to check that the idempotent elements ofare the form of(f,0)or(−f,1)wheref2=f.Since(a,0)is Q-clean infor everya∈I,we have either(a,0)=(f,0)+(u,0)or(a,0)=(−f,1)+(v,−1)wheref2=fand(u,0),(v,−1)∈.If(u,0)∈,then there exist elements(a,n),(b,m)∈such that((0,1)−(u,0)(a,n))⊥((0,1)−(b,m)(u,0)).Thus,

Since−a∈I,we have(−a,0)=(−f,1)+(v,−1)wheref2=fand(v,−1)∈.Then(−a,0)=(−f,1)+(v,−1)=(0,1)+(−f,0)+(v,0)−(0,1)=(−f,0)+(v,0).Since(v,−1)∈,we have(−v,1)∈.It follows from Lemma 3.2 that

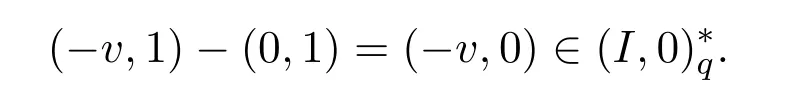
Thena=f+(−v)wheref2=f∈Iand−v∈.Therefore,Iis Q-clean.This,we complete the proof.

Theorem 3.2LetIbe a Q-clean ring(unitial or not)andA▹I.ThenAis Q-clean.

ProofWriteR=.Then(A,0)▹R.It suffices by(3)of Lemma 3.3 to show that(a,0)is Q-clean inRfor eacha∈A.But if−a=f+xwheref∈Id(I)andx∈,then(a,0)=(−f,1)+(−x,−1).This proves(1)of Lemma 3.3 because(−f,1)is an idempotent ofRand(−x,−1)=−(x,1)=−[(x,0)+(0,1)]∈by Lemma 3.2.This,we complete the proof.