不平衡数据的关键因素筛选方法＊

贾萍萍，李 扬＊＊

（1.中国人民大学应用统计科学研究中心 北京 100872；2.中国人民大学统计学院 北京 100872）

基于真实世界采集的数据中，常常存在分类数据的不平衡问题。如手术后患者是否死亡，死亡的人数很少，而存活的人数很多。在其他领域也有类似情况。当数据集中某一类或者某些类的样本量远远大于其他类时，即为类间不平衡。在这类数据中如果按照传统的模型评价方法，以最小化整体错误率作为模型选择的标准，那么少数类对整体精度的影响远小于多数类，导致分类器倾向于将测试样本判别为多数类，分类器在少数类上表现出较高的错误率[1]。这样变量选择与预测的结果均失去意义，因为在这些实际数据中数量少的一类样本更具分类意义，少数类的误判代价大于多数类的误判代价。

不平衡问题的处理方法主要分为两大类[2]：一类是从训练集入手，改变训练集样本分布，降低不平衡程度，例如使用各种采样方法和训练集划分方法，包括欠抽样和过抽样。欠抽样（Under-sampling）通过减少多数类样本使得数据达到平衡，缺点是会丢失多数类的一些重要信息，不能充分利用已有信息。过抽样（Over-sampling）通过增加少数类样本来使得数据达到相对平衡。随机过抽样是最简单的方法，它是在少数类样本中随机复制样本以达到增加少数类样本数的目的，但是容易造成过拟合。SMOTE抽样[7]通过合成新样本来增加少数类样本，在一定程度上避免了过拟合[3]。另一类是从学习算法入手，适当修改算法或者对模型评价的准则进行改进使之适应不平衡分类问题，如代价敏感[10]。代价敏感不会改变数据的分布，但是代价本身不容易衡量。

在研究疾病发生的影响因素，不良反应的影响因素等寻找“关键因素”的医学问题时，要考虑不平衡问题，同时也要考虑变量选择的方法。这类问题观测得到的有一些是分段数据，如年龄分段、用药剂量等，如果将分段的变量拆分成哑变量直接做回归，可能会出现同一个分段变量得到的哑变量有部分选择出来，部分未选择出来[11]。为了避免这种结果的产生，可以使用Group Lasso作为惩罚项，使得由一个变量拆分的一组哑变量同时被选入或者不被选入模型[11]。因此在分析这类数据时，可以将基础模型定为Group Lasso Logistic模型。

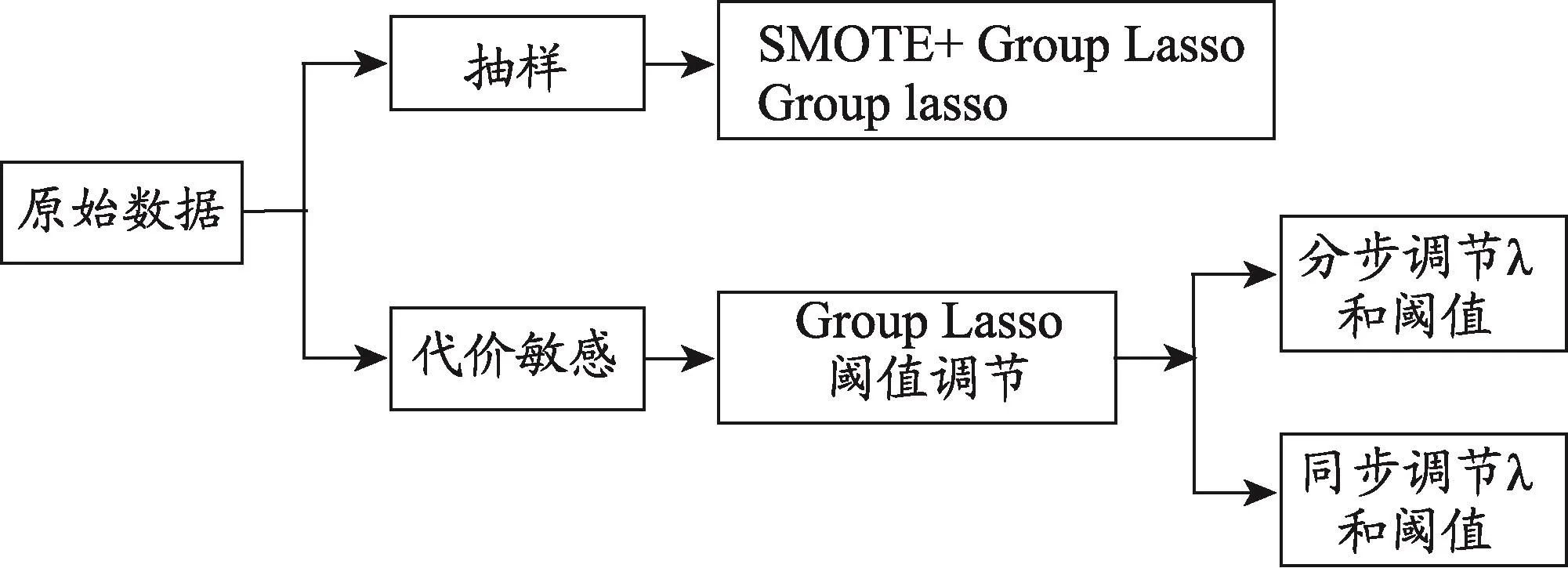
图1 研究思路示意图

Group Lasso的参数是通过最小化（1）式求解的，其中λ(λ≥0)是惩罚参数。参数λ的选择很关键，λ越大代表惩罚力越大，会有更多的系数压缩为0。

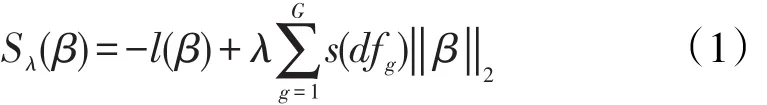
本文以Group Lasso Logistic模型为基础，从不平衡数据数据处理的角度出发，介绍了基于SMOTE抽样的Group Lasso和阈值调整的Group Lasso。全文共有4个部分，第1部分是研究背景，第2部分是研究方法与思路，第3部分通过实例应用分析比较不同方法的结果与适用性，第4部分是总结讨论与研究展望。

1 研究方法

为了解决数据中的不平衡问题,可以从数据层面出发，通过抽样改变数据的分布，使之达到平衡。但是由于抽样具有一定的随机性，过抽样可能会导致过拟合，欠抽样会损失一定的信息[5]。从少数类和多数类误判代价不同的角度出发，有研究者提出了改变预测阈值的方法来对不平衡数据建立分类模型[6,8]。这本质上是代价敏感的体现，即认为少数类的错误代价高于多数类。本研究从数据和代价两种视角，用三种方法进行变量选择，并比较方法的优劣。研究思路如图1。

基于SMOTE抽样的Group Lasso方法，使用交叉验证选择（1）式中损失最小的λ，得到最优模型，从而筛选出关键因素。阈值调整的Group Lasso是基于2013[6]年和2014[8]年李扬等提出的调整预测阈值方法，分步调参或同时调参，前者先选择出“最优”的惩罚参数λ，再调节预测阈值，后者是同时选择惩罚参数和预测阈值，以筛选出关键因素。

三种方法使用了TPR、FPR、AUC、G-Means等模型评价指标。如果用TP表示实际为正类的样本中预测为正类的个数，FN表示实际为正类的样本中预测为负类的个数，FP表示实际为负类的样本预测为正类的个数，TN表示实际为负类的样本预测为负类的个数，那么：

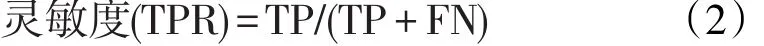
即真正为正类的样本被预测为正类的比例,又称为真阳性率。

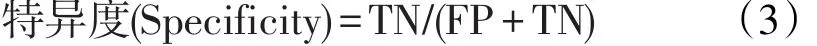
即实际为负类的被预测为负类的比例，1-特异度即为假阳性率。

对于很多分类器，最终输出的是一个概率，如果阈值选择不同，那么相应的TP、FP等取值就会改变，由此引出了ROC曲线。ROC曲线以灵敏度（TPR）为横轴，以1-特异度（FPR）为纵轴，刻画了某个分类器在不同分类阈值下的TPR和FPR变化情况，是对模型预测效果的综合评价。

G-Means是对灵敏度和特异度的综合评价指标，公式如下：

1.1 基于SMOTE抽样的Group Lasso

2002年，Chawla等提出SMOTE（Synthetic Minority Oversampling Technique）抽样方法。SMOTE算法的思想主要是：假设X是一个少数类样本，寻找X的k个同类最近邻样本，假设采样的倍率是n，则在这k个样本中选择n个，记为Ci(i=1,2,…,n)，在少数类样本X和Ci之间随机线性插值，生成新的样本Zi。这种方法一定程度上避免了过拟合[7]。插值的公式：

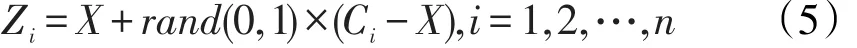
本研究采用基于SMOTE抽样的group lasso方法，方法如下：

第一步：在原始数据上进行SMOTE抽样，得到新样本集合Sj(j=1,2,…，100)

第二步：在Sj中采用5折交叉验证选择最优的λ,得到最优的模型Mj和选择出的变量数gj。

第三步：由于SMOTE抽样改变了一部分数据，在平衡的数据上选出最优的模型后，更关注的是在原始数据上的效果如何。因此利用最优模型对原始数据进行预测，得到ROC曲线下面积AUC；

第四步：调整阈值，计算不同阈值对应的TPR、FPR以及G-Means。

1.2 基于阈值调整的Group Lasso

1.2.1 分步调参

Logistic模型得到的结果是预测的概率,而预测阈值（Cutoff）是最终进行预测的参考依据。当预测概率大于阈值时，预测结果是少数类（正类），当预测概率小于阈值时，预测结果是多数类（负类）。不同的阈值对应着不同的灵敏度和特异度。2014年，李扬等提出了分步骤调节参数和预测阈值使得灵敏度和特异度均达到较高水平的方法。方法如下：

第一步：λ选择过程

采用AUC作为模型选择的标准，对于不同的λ，计算模型预测的AUC。选择AUC最大时的λ作为最优的Group Lasso的调节参数。

第二步：Group Lasso过程

根据第一步选择的最优λ，运用Group Lasso Logistic模型选择变量。由同一个变量产生的哑变量作为一组。采用分块坐标下降的方法进行参数估计。

第三步：预测过程

由模型得到的是预测的概率，选择不同的阈值来划分多数类和少数类，会得到不同的灵敏度和特异度。阈值越大灵敏度越小而特异度越高。在灵敏度和特异度上进行一个综合考虑，选择一个合适的阈值作为预测阈值。

1.2.2 同步调参

分步调参的过程将λ的选择和阈值的选择分开进行，两个过程不一定能够同时达到最优。为解决这一问题，李扬等在分步调参方法的基础上进行了改进，提出同时选择λ和预测阈值的方法[8]。方法如下：

第一步：在不同的λs下运用Group Lasso Logisitc模型；

第二步：将数据分成K折，X1,X2,…,Xk；

第三步：对选择的每一折Xi（i=1,2,…,K）作为验证集，剩下的K-1折作为训练集，在不同的λs下对训练集建立模型；预测阈值选取从0-1,步长为0.01,在每个阈值下分别计算Xi的TP和FP。计算不同λs和预测阈值对应的G-Means；

第四步：计算平均G-Means：

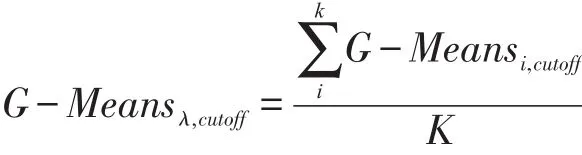
第五步：根据计算的两个指标选出最优的λ和预测阈值，将对应的结果作为最优的模型。

2 应用分析

全球有70%的人处于亚健康状态(Suboptimal Health State,SHS)[6]。传统中医通过“辨证论治”的理论将人群分成不同的类别进行治疗，在治疗亚健康状态方面有非常突出的优势。“肝郁脾虚”是中医临床中一个常见症候[4]，为寻找“肝郁脾虚”的人群特征，有6家医院收集了307例亚健康患者问卷数据，其中诊断为肝郁脾虚的患者有57个，非肝郁脾虚的患者有250个，二者的比例为1∶4.39，数据存在不平衡。两组人群在年龄、性别两个维度上没有差异。评估是否为肝郁脾虚的症状有22个（表1），每个都有5个水平，最后的哑变量有88个。使用基于SMOTE抽样的Group Lasso和阈值调整的Group Lasso方法来寻找诊断“肝郁脾虚”的关键因素，并建立诊断模型。

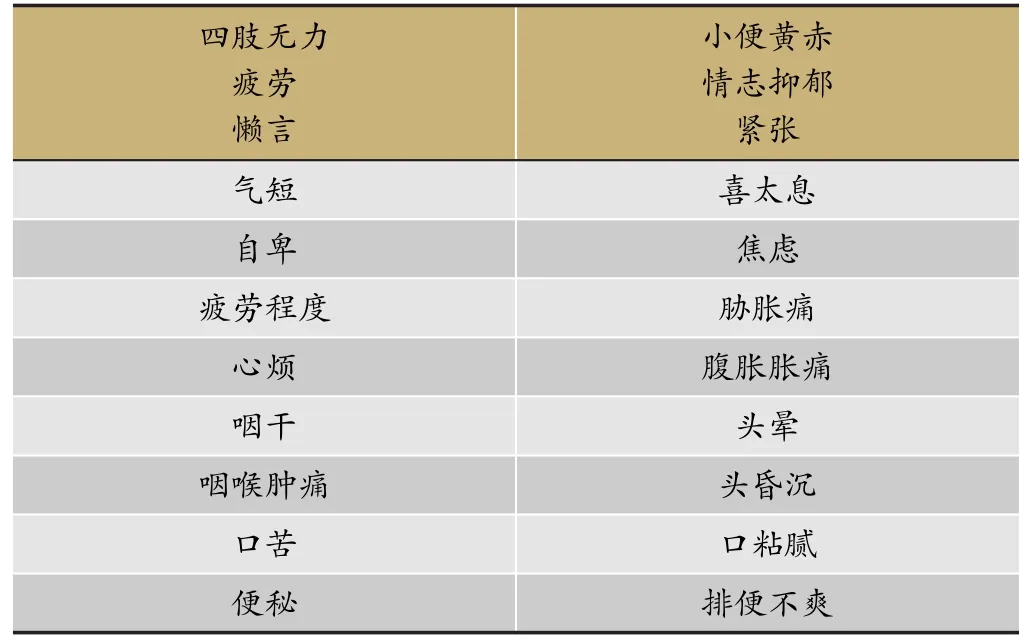
表1 预测是否肝郁脾虚的症状*

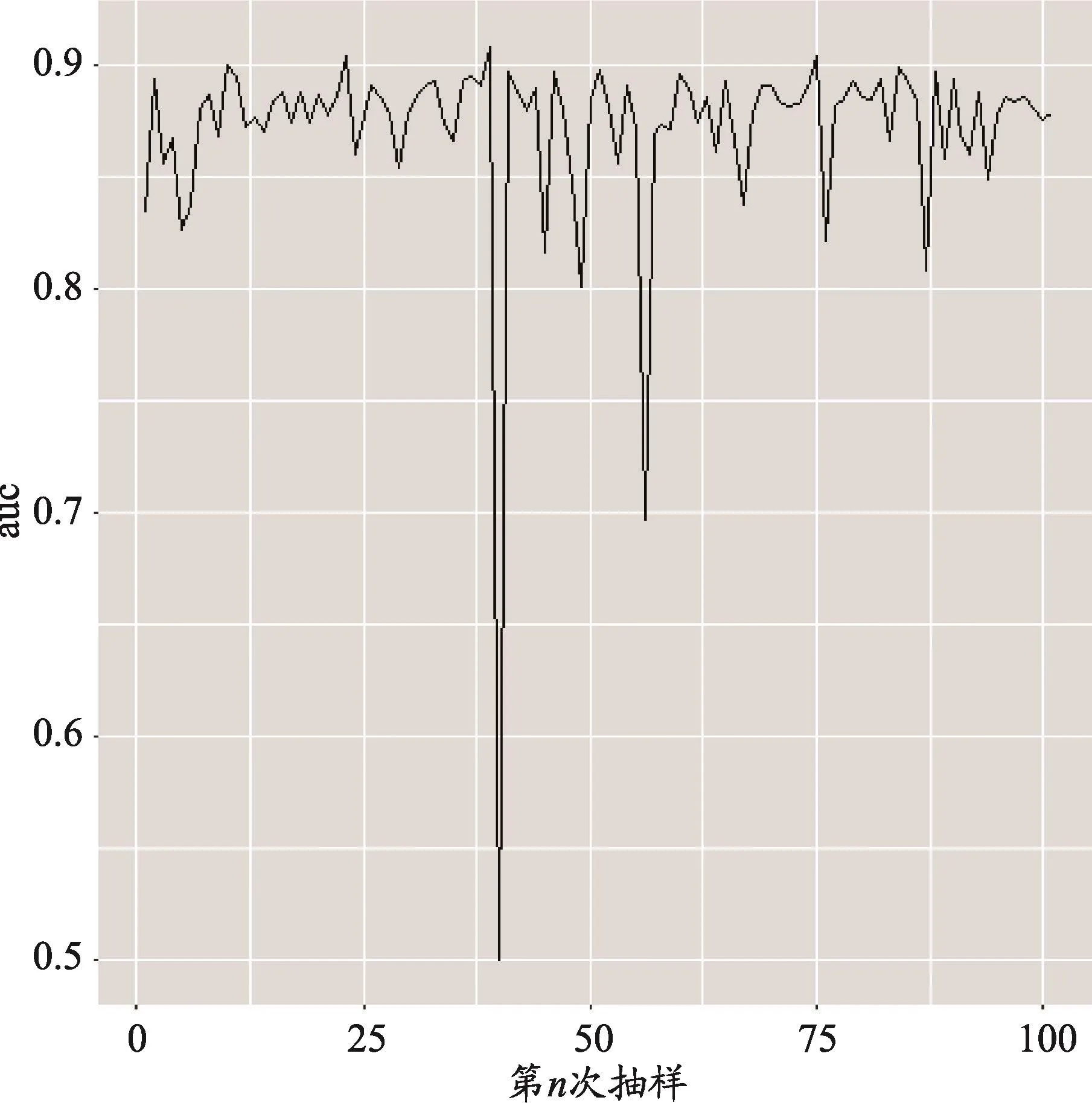
图2 100次抽样结果的AUC

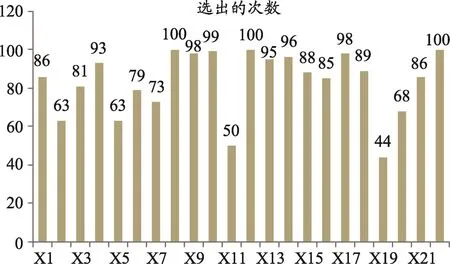
图3 100次抽样变量选择情况

由于SMOTE抽样具有一定的随机性，所以重复进行了100次抽样，分别得到100个模型结果。图2表示的是SMOTE抽样方法得到的100个模型在总体中的AUC结果，图3是100次变量选择中22个变量被选出的频数。从图2可以看出，100个AUC大部分在0.85左右，但是个别抽样结果得到的AUC低至0.5，说明了单次抽样结果不稳定，使用抽样方法解决不平衡问题时，不能仅仅根据一次抽样得到的结果下结论。

三种方法最终选择的变量结果如表3，所选择的变量中大部分都是肝郁脾虚诊断使用较多的症状[4]。

表3表示的是阈值调整的两种方法得到的预测效果。表中的数字代表灵敏度和1-特异度，例如当患有肝郁脾虚的人中有98.2%的被预测为患病时，没有得肝郁脾虚的人中，有91%的被错误预测为患病。如果更加关注灵敏度，则需要把阈值调低。

基于SMOTE抽样的Group Lasso最终得到的模型结果显示，在阈值为0.17时得到最大的G-means,对应的灵敏度为0.77，特异度为0.76。而同时调参的阈值调整方法在阈值为0.15时得到最大的G-Means,对应的灵敏度为0.89,特异度为0.64。作为一个诊断模型，更加关注的是真正患病的人能否得到诊治，也就是更加关注灵敏度，基于这一点同时调参的阈值调整方法更好。

3 讨论

基于SMOTE抽样的方法和基于阈值调整的方法，分别从数据角度和模型评价的角度来解决由不平衡带来的问题。基于抽样的结果会受到抽样比例的影响，也具有一定的随机性，例如从图2可以看出，有些抽样结果表现比较差。当少数类样本的数量本身就比较少时，如果生成过多的新样本，会使得噪声对模型的干扰增加，这时不建议使用抽样方法。通过抽样得到的最后结果，和阈值调整的思想结合起来进行判断才能得到一个相对合适的分类模型。基于阈值调整的方法，在参数选择上，显然使用交叉验证同时选择更为合适。从结果上看，基于SMOTE得到的结果比阈值调整中的分步调参要好。考虑到模型为诊断预测模型，更加希望真正患病的病人得到正确诊断，即更加关注灵敏度，同时调参得到的结果较好。如果在基于SMOTE的方法中使用同时调参的思想，或许会得到更好的结果。

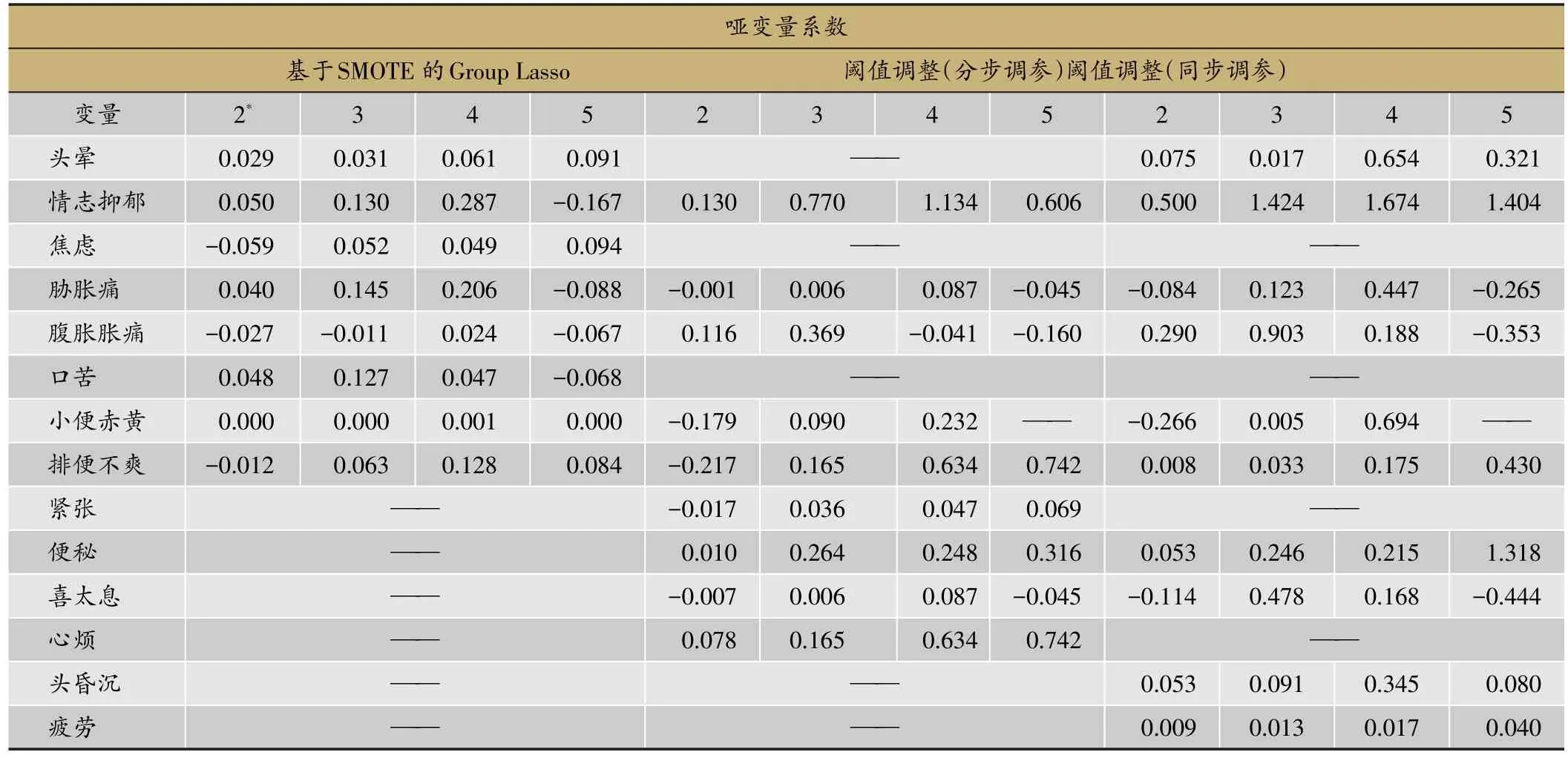
表2 选择的变量及其系数

通过上述比较，我们可以认识到在建模时，选择合适的评价指标非常重要，对于不平衡数据带来的问题，有很多解决的方法，我们也应当选合适的方法去解决这个问题，否则会造成模型得到的结果实际上并不能准确反应实际结果的情况。通过抽样来改变数据的分布是比较方便的解决办法，但是需要进行阈值的判断才能得到比较好的预测效果。在使用其他方法时，引入调整阈值的思想，比直接使用一个临界值作为判断阈值得到的结果要好。

实际数据中除了类间不平衡问题，还存在类内不平衡问题，即在某一个类别内，不同子集的数目相差很大。本研究仅仅考虑了类间不平衡问题，未来的工作重点可以放到类内不平衡问题上。在未来的应用及研究中，如果使用了Lasso的方法，最好将Lasso的参数选择和模型的选择放在一起考虑，同时调节参数才能得到真正最优的结果，否则只能得到某个参数条件下的局部最优结果。实际上，不仅仅是Lasso,涉及到两个及以上的参数调节的问题，都需要从全局最优的角度考虑。

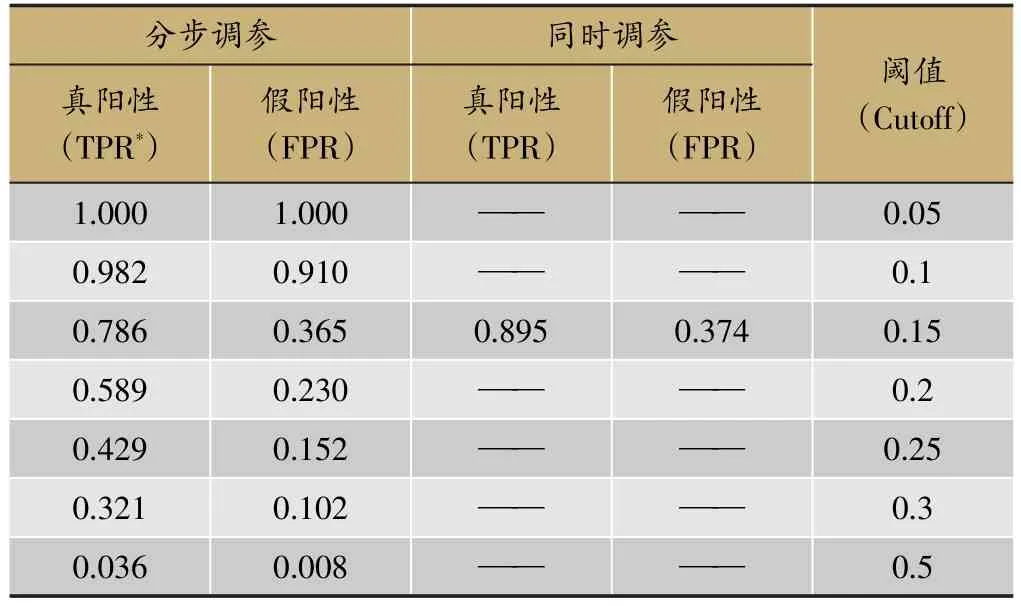
表3 基于阈值调整方法得到的TPR和FPR