精准诊评答疑解惑，经典习题同类跟进—— 从几则“在线”答疑案例说起

☉江苏省苏州市工业园区东沙湖学校西校区 左爱娟

郑毓信教授曾在《人民教育》发表系列文章推介数学教师的专业基本功，如“善于举例”“善于提问”“善于比较和优化”，这些在课堂教学中显得非常重要.除此之外，个别辅导或作业批改时，教师还需要具备答疑解惑的专业功夫.最近“在线”给学生的一些错题进行诊评并答疑辅导，取得较为理想的答疑效果，引发笔者对“在线”答疑辅导的一些思考.检索文献，发现早有“先行者”（详见参考文献［1］～［2］）.本文先梳理几个“在线”答疑的案例，并阐释相关思考，供研讨.

一、“在线”答疑辅导案例展示

题1：如图1，在四边形ABCD中，AC=BD=6，E、F、G、H分别是AB、BC、CD、DA的中点，则EG2+FH2=______.

思路诊评与点拨：从学生标注的4个3及EG⊥HF看，思路已接通，可能是运算上出错.一个有效的建议是，设GE、FH交于O点，恰当设元，设HO=x，GO=y，由勾股定理得x2+y2=9，待求的GE、FH的平方和是4（x2+y2）=36.可见，几何演算类问题，恰当引入参数可以简化推理演算的表达式，使得我们避免复杂大写字母的运算处境，这是值得分享和积累的经验.

图1

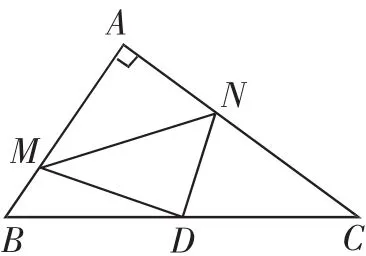
图2

题2：如图2，在Rt△ABC中，∠A=90°，AB=6，AC=8，点D为边BC的中点，点M为边AB上的一动点，点N为边AC上一动点，且∠MDN=90°，则cos∠DMN为______.

思路诊评与点拨：学生原有思路（过点M、N作两条垂线段）虽然有一些进展，但对于目标（∠DMN的余弦值）没有很快接近，反而陷入复杂的运算.这种辅助线构造不利于接近目标，需要“折返”“调头”.（随感：一个优秀学生、有智慧的人应该有“调头”的勇气）

思路1：过点D分别向AB、AC作垂线段DG、DH，垂足分别为G、H，可利用相似三角形处理……最终导出DN∶DM的值，这是∠DMN的正切值，思路就接通了.

思路2：把目光投向四边形AMDN，双垂直？对角互补吗？是否四点共圆？确认这些之后，连接AD，可将∠DMN转化为∠DAN，从而快速转化为∠C的正切值，答案只需口算.（当然，运算简单的方法需要付出逻辑思维的代价.对于一名优秀学生来说，应该思路开阔，即“思维向四面八方打开”）

题3：将一副三角板（如图3）摆放在一起，组成四边形ABCD，连接AC，则tan∠ACD的值等于______.

图3

思路诊评与点拨：学生原有作高（作AC边上的高）的想法，没有走通，但这种念头是有效的，可以调整为构造CD边上的高AF，将“右下角”补全成等腰直角三角形BDE，就能顺利突破思路.这里有一个关键是“增量巧设”（与学生原有设法相比，更有利于后续演算），即设AB=a，于是可得出BD=BE=a，BC=CE=a，再把目光投向等腰直角三角形AEF，就可想清CF、AF的长了，从而获得思路贯通.

题4：二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图像如图4所示，则ax2+bx+c=m有实数根的条件是______.

思路诊评与点拨：学生原有答案（-m≥5）莫名其妙，解集表达形式上怎么也不能写-m啊.直接看出答案，视ax2+bx+c=m左边为图中抛物线“不动”，将右边视为动直线y=m，可直观看出直线与抛物线有交点时，m≥-2.这道题的解题策略是“以形助数”，提供以下两道习题，作为同类跟进.

图4

图5

同类链接1：二次函数y=ax2+bx+c的图像如图5所示，试分析关于x的方程ax2+bx+c-3=0的根的情况.

同类链接2：若二次函数y=x2+bx的图像的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解为（ ）.

A.x1=0，x2=4 B.x1=1，x2=5

C.x1=1，x2=-5 D.x1=-1，x2=5

二、关于答疑解惑的几点思考

1.深刻理解习题结构，能从不同角度贯通思路

给学生答疑辅导之前，需要先深刻理解习题的结构特点，尝试从不同的角度贯通思路，并且明辨不同解法的繁简、优劣，这样才能站在更高的高度理解学生的思路、错误及思维障碍之处.特别是，教师的解法研究要尽可能体现“回到定义”的“初等解法”，因为当学生思路受阻时，需要及时引导他们回到“回到定义”的“自然而然的解题念头”，而不是简单化地转化为一些个性化的“模型”“模式”.当然，一些重要的“解题模型”、转化策略或求解经验也可通过由简单的问题出发帮助学生推导确认，用于一些较难习题的有效转化.这些理解习题的功夫其实都是后续精准诊评、解惑的基础.

2.认真阅读学生解法，读懂已有进展精准诊评

教师在深刻理解习题的结构与解法之后，接下来就是认真分析学生的解法，由于在线答疑并不是面批或当面答疑，所以无法开展即时对话，特别是学生对问题有怎样的理解进展、想法只能根据“图片”（更多情况下是所拍照片）上遗留下来的一些解题痕迹，如演算草稿或图形上的分析痕迹进行诊评.根据这些答题痕迹，我们要尝试理解学生的思考方向、已有进展，并开展精准诊评、提出解题建议，在引导解题思路时最好能从学生已有进展或已有念头出发，使之不断丰满，接近解题目标，如果出现错误的解题方向，则需要恰当引导，让学生有“敢于调头”的解题勇气和智慧.

3.经典习题解法错漏，需要同类跟进修补漏洞

答疑解惑过程中遇到的习题会有很多类型，教师在遇到一些经典习题时，要保持敏感，引导学生重视经典问题，在剖析错误原因、贯通思路之后，要引导学生进行解后回顾与反思：还有哪些解法？不同解法需要体现哪些领域的知识或性质定理？等等.在此基础上，需要像上文“题4”一样，给出同类习题的链接跟进，让学生在订正之后有同类题的变式再练，以有效提高对这类习题的处理能力.

4.答疑解惑是基本功，值得教师长期修炼精进

师者，所以传道授业解惑也.数学老师的答疑解惑能力应该是一项专业基本功，这项专业基本功的背后是教师扎实的解题能力，阅读、倾听学生的能力，恰当、精准诊评学生的能力，特别是，除了解题思路的贯通，还要向学生传递解题信心，鼓励学生不怕困难、迎难而上，又要有善于调头、回到起点再出发的勇气.此外，答疑辅导不宜直接告知答案或思路，要通过恰当的设问与诱导，使学生能自主发现解题思路并获得最后解答，这样对于保护学生的解题信心是非常重要的.

三、写在后面

教学即研究，教育现场无处不在.本文关注的是答疑解惑这个常见的教学话题，但是“至小无内”，如果深入下去，不同教师的答疑解惑的水平和功夫差异是巨大的，当我们以精湛的答疑解惑能力呈现在学生面前时，收获的是教师的专业威信，还有来自学生和家长的敬佩.让我们共同努力，期待更多答疑解惑案例的分享，促进这类课题的研究更丰富和深入.