走进函数综合，解法探析思考——以一道函数综合题为例

☉江苏省常熟市白茆中学 张建亮

函数综合题在中考中常以压轴题的形式出现，该类试题综合了众多的知识内容，题型变化多样，综合性强，对学生的解题思维要求较高.本文以一道函数与几何的综合题为例开展解题探究，分析思考，并提出相应的教学建议，与读者交流.

一、问题呈现

图1

（1）试求点B的坐标及抛物线C的解析式.

（2）若点M（m，0）为x轴上的一个动点，过点M作x轴的垂线，与直线AB相交于点P，与抛物线C相交于点N.

①若点M在线段OA上运动，当B、P、N三点组成的三角形与△APM相似时，试求点M的坐标.

②若点M可在x轴上自由运动，定义：如果M、P、N中恰好有一点为其他两点所连线段的中点，则称M、P、N三点为“共谐点”.请写出M、P、N三点为“共谐点”时参数m的值.

二、思路分析

本题目为初中常见的函数综合题，是以直线和抛物线相交为背景而构建的.第（1）问求解相关点的坐标及函数的解析式，属于常规问题.第（2）问是以点动为基础命制的考题，第①问分析三角形相似的情形，第②问求解新定义下的参数值，是本考题的难点所在.问题涉及解析式求解、动点分析、三角形相似，以及线段中点等内容.

第（1）问求解点B的坐标关键是明晰该点与直线、抛物线及坐标的关系，求解抛物线的解析式，实际上就是求解析式中b和c的值，从方程角度出发，需要求解抛物线上的两个点，构建二元一次方程组.

第（2）问表明点M为x轴上的动点，点M运动必然会影响△BPN的形状，第①问分析△BPN与△APM相似时的情形，则需要分析△BPN和△APM的特性，在函数背景下利用“对应角相等，对应边成比例”的判定定理解题.第②问定义了“共谐点”，则首先需要理解定义的内容，即三点中，其中一点为另外两点连线的中点，基于该定义来讨论三点之间的关系，将其位置关系转化为坐标之间的数量关系.

三、解答过程

（2）①由题干可知PM始终垂直于x轴，故△APM为直角三角形，则tan∠PAM=.△BPN和△APM始终存在一组对顶角，故只需要确保另一组内角相等即可，即△BPN中也存在一个90°的角.下面分别讨论：

（ⅰ）当∠BNP=90°时，如图2所示，直线BN平行于x轴，则点B和点N必然关于抛物线的对称轴对称.点B的坐标为（0，2），抛物线C的对称轴为直线x=，所以点N的横坐标为，即点N的坐标为 （， 2），所以点M的坐标为 （，0）.

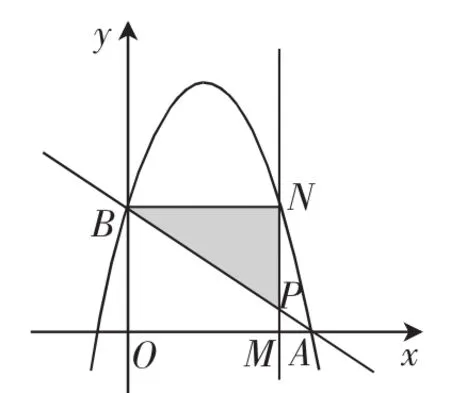
图2

图3

（ⅱ）当∠NBP=90°时，过点B作MN的垂线，垂足为点H，如图3所示，则tan∠PNB=tan∠PAM=.点H的坐标为（m，2），点N的坐标为则BH=m，HN=-m，则，解得m=，所以点M的坐标为

②存在以下三种情形.

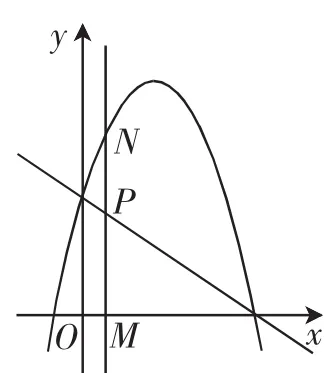
图4

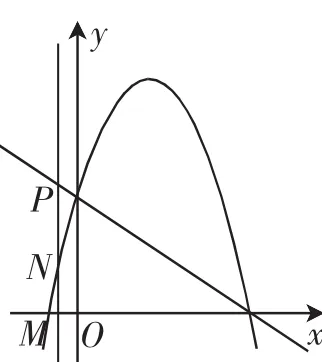
图5

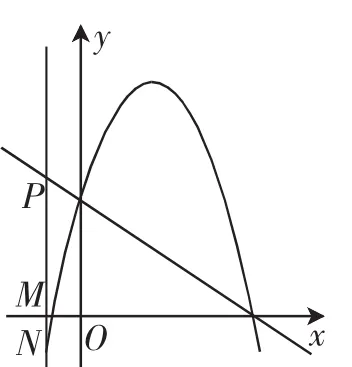
图6

（ⅰ）点P为NM的中点，如图4，则MN=2PM，即点N的纵坐标为点P的纵坐标的2倍，可得方程m+2=），解得m=3（舍去）或m=.

（ⅱ）点N为PM的中点，如图5，则PM=2NM，有yP=2yN，可得方程m+2，解得m=3（舍去）或m=-.

（ⅲ）点M为PN的中点，如图6，则PN=2PM，点P和点N关于x轴对称，PM=MN，则有m+2=解得m=3（舍去）或m=-1.

四、解后思考

本题目为函数综合题，在中考中一般以压轴题的形式出现，除了考查学生对函数基础知识的掌握，还常通过知识融合考查学生综合运用知识的能力.上述就是函数与几何知识的融合，考查几何性质与函数之间的联系，具有一定的代表性，下面对试题进一步思考.

1.考题的命题特点

考题以直线与抛物线为背景，考查函数与几何知识的联系，其特殊性在于构建了一个动点，第（2）问以点动为依托，分别引入了三角形相似和几何新定义.题目具有很强的拓展性，知识的衔接较为紧密，既能考查学生对两大知识领域的联系性的把握，又能考查学生全面分析问题、转化问题的能力.

2.解题的关键步骤

总体而言，本题目属于函数动点问题.第①问分析动点函数背景下的三角形相似，解题的关键是把握两个三角形的特性——存在对角且△APM为直角三角形，需要基于该特性，结合三角形相似的判定定理来构建思路，将问题转化为分析点的坐标或线段长.第②问属于几何新定义题，看似复杂，实则是分析线段中点的问题，关键是全面考虑“共谐点”的三种不同情形，将中点性质与点的坐标的关系相联系.

3.值得学习的方法

上述在处理线段动点时采用了“参数表示，化动为静”的方法，即设定动点的坐标，将所求点的线段长用含有动点坐标的参数来表示，然后结合条件探寻线段之间的等量关系，构建相应的代数方程.因此学会动点问题的简化策略很重要，而动点的参数化是其中较为有效的一种方法，需要注意的是，要关注参数的取值范围，确保定义的正确性.

4.常见的变式形式

上述与几何相结合的函数综合题在中考中很常见，其问题类型也较为多样，可以对本题目的第①问适当变式.

变式1：当B、P、N三点组成的三角形与△APM相似时，试求△BPN的面积.

参考思路：解题的关键依然是把握三角形的特性，构建相似的情形，从而确定点M和点N的坐标.考虑到两个三角形为直角三角形，因此可以直接由点的坐标转化为对应的线段长，然后基于三角形的面积公式求解，有两种思路：①直接求得△BPN的底和高；②求解两三角形的相似比，求出△APM的面积，然后用相似比转化.后者看似复杂，但考虑到相似的情形有两种，△BPN的位置发生变化，而△APM的位置基本不变，更容易分析.

变式2：在x轴上是否存在一点N，使得B、P、N三点组成的三角形与△APM全等？若存在，请求出点N的坐标；若不存在，请说明理由.

参考思路：该变式为常见的存在性问题，分析时同样可以参考上述解题的思路，先构建相似，然后引入一组对边相等即可.因此可以把握其中的直角特性，确定点的大致分布.对于分类的第（i）种情形，点P必然为MN的中点，从而确定点N的坐标.对于第（ii）种情形，则需要进一步考虑AM=BN.因此对于全等问题，可以转化为分析相似比为1的三角形相似问题.

五、教学建议

1.注重思路讲解，掌握解题策略

函数综合题具有很强的知识综合性，在教学中开展对应的解题教学可以加速学生的知识融合，提升学生的解题能力.教学时特别需要注重引导学生掌握问题的转化方法和构建思路.如上述函数背景下的相似问题，应转化为分析平面直角坐标系中线段和点的坐标的关系，构建对应的代数方程来确定点的坐标.对于新定义题，则需要引导学生认真读题，理解定义，然后结合题干条件分析定义下的问题，将其转化为简单的函数或几何问题.问题是变化多样的，但解题的方法和策略是不变的，教学中应注重学习方法指导.

2.渗透解题思想，提升解题思维

求解综合类考题离不开解题的思想方法，利用数学思想方法可以全面分析问题，使问题简单化，提高解题效率.如上述解题过程利用了分类讨论和数形结合思想，正是在上述两种思想的配合下，使得问题更为直观，分析过程更为严谨，从而确保了答案的正确性.因此，在教学中不仅需要指导学生解题，还需逐步渗透数学的解题思想.考虑到思想方法较为抽象，教学时可以结合具体的内容，如在讲解抛物线时渗透数形结合思想，利用“数”与“形”的结合帮助学生掌握抛物线的特性.数学思想方法是思想层面的内容，通过数学思想的渗透可以在潜移默化中提升学生的解题思维，从根本上提升学生的解题能力.