微专题复习：值得重视的一类课型——以“黄金分割”专题复习课为例

☉江苏省苏州高新区实验初级中学 丁 香

黄金分割是一个非常重要的知识点，各种版本的教材都在不同章节通过例、习题或数学活动进行渗透，作为中考复习，有必要将黄金分割作为一个专题复习.本文是笔者设计的一节“黄金分割”专题复习课，整理出来，供研讨.

一、“黄金分割”专题复习活动设计

活动1：复习黄金分割的定义

问题1：如图1，点C在AB上，AC∶AB=BC∶AC.若AB=1，求AC的长.

图1

预设：学生利用一元二次方程解出AC的长为之后，给出黄金分割比值，指出它的近似值通常用0.618表示，进一步给出定义.

定义：黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值

运用定义解释以下尺规作图：

如图2，以AB为直角边作直角三角形ABC，使∠ABC=90°，BC=AB，在斜边AC上取CP=CB，再在AB上取AG=AP.则点G为线段AB的黄金分割点.

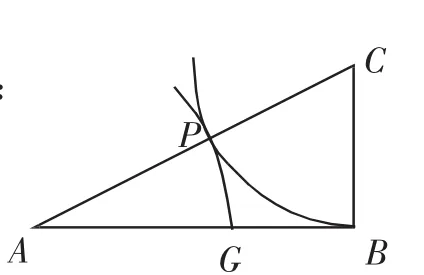
图2

活动2：认识黄金三角形

问题2：如图3，在等腰△ABC中，顶角∠A=36°，BD为∠ABC的平分线.

（1）求证：AD=BD；

（2）图中有三角形相似吗？

（3）若AC=2，求底边BC的长.

教学组织：在学生练习之后，引导他们根据黄金分割的定义，确认点D为边AC的黄金分割点，这种三角形常常称为“黄金三角形”（顶角为36°的等腰三角形），它的底边与腰长的比值为

图3

活动3：找一找黄金分割点

问题3：以下构图简单、自然，却能得出黄金分割点，你能说明理由吗？

（1）如图4，分别以BC为一边向两侧作等边三角形ABC和正方形BCDE.以点C为圆心、CE为半径画弧，与射线AB交于点F.则B是线段AF的黄金分割点.

图4

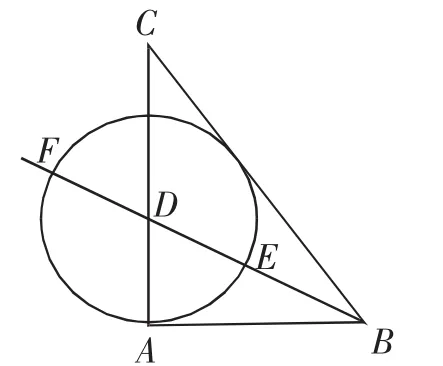
图5

（2）如图5，先构造边长分别为3、4、5的三角形ABC.作角B的平分线，与边AC交于点D.以点D为圆心、DA为半径作圆，与角平分线分别交于点E、F.则E是线段BF的黄金分割点.

（3）如图6，画一个含30°角的直角三角形ABC，∠ABC=30°，∠C=90°.取AB的中点E，以点E为圆心、AB的长为半径画圆，与CB的延长线交于点D，则B为线段CD的黄金分割点.

教学组织：通过几个好懂的作图得出黄金分割点，安排学生“回到定义”去判断，加深对黄金分割比值的理解.

图6

活动4：考题中的黄金分割

问题4：如图7，菱形ABCD中，点E是对角线AC上一点，且EA=AB，EB=EC=ED=1，求菱形的边长.（至少两种方法求解）

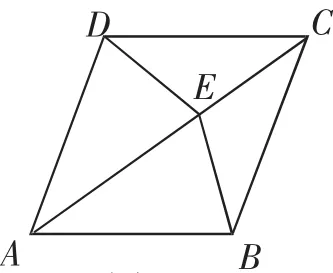
图7

解法预设：

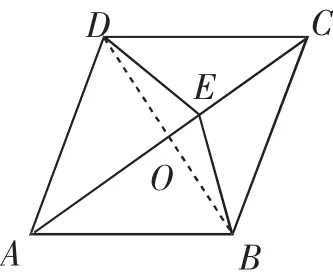
图8

解法1：如图8，连接BD交AC于点O，设菱形的边长为x，则在直角三角形AOD、直角三角形DOE中，利用公共边DO，可得关于x的方程，解得x=

解法2：可证△CDE∽△CAD，可得CD2=CE·AC.设菱形的边长CD为x，可得x2=1·（x+1），解得

解法3：设∠CDE=α，容易导出∠DCE=α，∠DAE=α，∠ADE=∠DEA=2α.在△ADE中，利用三角形内角和可求出α=36°，于是△ADE是黄金三角形，底边DE=1，则腰长为，即菱形的边长为

教学组织：先安排学生独立练习，然后组内展示不同解法，最后由小组派出代表上台讲解，教师点评时注意引导学生识别黄金三角形.

二、教学立意的进一步解读

1.深入研究教材，挑出在不同分册的素材与题例

教材编写者对一些经典问题或奇异性质往往采取分批呈现、螺旋上升的安排方式，像本文关注的黄金分割的经典图形，在八年级上学期学习等腰三角形时就出现过“黄金三角形”，但是由于当时还没有相似的知识，也没有一元二次方程的知识储备，所以对“黄金三角形”的研究并不深入，所以这个图形在本专题复习中得到全面关注和研究.此外，有些教材在图形认识初步学习时，让学生通过画四边形，并取四边中点得到“中点四边形”，学生通过度量、猜想发现中点四边形的性质，但由于没有学到平行四边形、中位线的性质，所以在七年级时没有进行证明，这也是不同分册的教材对经典问题、奇异性质的分批呈现与螺旋上升，我们在中考备考复习时就要注意抓取这些素材，引导学生“再认识”.

2.检索各地考卷，精选体现黄金分割考点的习题

研究中考试题是很多同行的兴趣，特别是针对一些较难的综合题进行解析更是不少教研群（QQ群、微信群）的主要内容，然而针对经典问题（如黄金分割）这样的专题研究不是很多，似乎研究考题一定有要“猎奇”的追求.我们通过检索各地考卷发现，在不少地区（如上海、安徽等地）关键考题的位置上都隐含考查了黄金分割的考点.需要注意的是，这种检索并不是按关键字、关键词来检索，而是需要认真解题，在演算过程中发现试题中存在黄金分割的结构特征，这类习题就需要被抓取出来，作为归类收集的重要素材，为日后研发黄金分割习题课积累资料.

3.注重演算说理，呈现数学问题预设多解与追问

黄金分割的相关作图、构图方法很多，如何带领学生解读、理解这些方法也是备课阶段重点考虑的.在上面的课例中，我们提供了4种较为典型的构图方法，为了节约课堂时间，没有安排学生模仿作图，而是安排学生对这些构图方法进行解读、演算，通过运算确认构图方法的正确性，也感受到黄金分割的奇异之美.另外，对一些典型问题还预设了不同思路，要求学生运用不同方法解答，体现思维的发散性，同时不同的解法也对应着不同知识模型，体现黄金分割与多个不同知识模型的广泛联系.

三、关于微专题复习的两点思考

1.值得重视的微专题复习课型

我们注意到高考备考阶段特别重视微专题的复习研讨活动，在中考复习阶段也有不少教师积极尝试，开展了中考微专题复习课型的建构与推介，这些都给我们积极启示.从教学实践来看，微专题复习课能让学生更有参与的热情，充满探索新知的兴奋与乐趣，是值得我们积极参与的一类课型.相比传统的中考复习分一轮、二轮，微专题复习这种“八股化”做法，以某一个知识点或主题推进复习进程，所选习题跨不同年级，形散神聚，让学生有“一线串珠”的感觉.

2.微专题复习课重在精选主题

微专题复习课的备课选题需要教师长期积累，特别是针对本地区中考试题、课本例题和习题有深入的对比研究，能敏锐地抓取出一些典型问题，挑选出一些有价值的研究主题，然后将这些典型例、习题或考题在某一个主题下由易到难“串题成课”，使得一节课下来，学生训练不同章节的习题，但都是聚焦某一条主线，渐次展开.上文关注的黄金分割，其实还可以主题关注“围长方形问题”，从七年级的字母表示数、一元一次方程，到八年级的整式乘除、因式分解、分式运算，再到九年级的一元二次方程、二次函数等，都可以聚焦“围长方形问题”；再比如，聚焦“三个一次”，关注一元一次方程、一元一次不等式、一次函数之间的联系，等等.这些都是值得研究的微专题复习课.