在概念内涵发展中提升学生的备考能力——以圆和圆的位置关系为例

☉江苏省睢宁县第二中学 朱 振

学生进入初三，中考备考随之而来，在初三下学期数学学科基本上都是复习了.为了科学备考，让学生进一步明确考向，学校近期举行了一次关于图形与几何的公开课，经过集体备课后让青年教师晒课，再集体打磨，让我校初三数学备课组形成了合力.

一、分析近年来数学试卷的特点，研究课堂教学的程序

集体备课时，我们带来了近三年的中考数学试卷.展开这些中考试卷不难发现，试题重视对学生发展必需的核心知识、基本技能的考查的同时，还注重对数学思考、解决问题能力和数学活动过程的考查.其中，图形与几何方面的综合考题植根于圆的性质等知识的整合，以及平面几何图形的有关计算问题等方面.为此，本节内容选定为圆和圆的位置关系，从学习目标、知识再现和试题突破等环节进行教学，由激情四射的青年教师刘老师晒课.

二、课堂实录

1.教师通过电子白板向学生展示学习的三维目标并解读

（1）知识目标：通过相交两圆、相切两圆的复习，发展学生对概念与性质的认知能力；

（2）能力目标：通过相交两圆、相切两圆的性质探究，提升学生的读图能力和动手操作能力；

（3）情感与价值观目标：体验数学活动充满着探究与创新，感受中考数学命题蕴含着科学的数学思想.

2.通过图像展示，让学生明确两个圆的位置关系的概念，并进行展示

［电子白板展示］在图1中，⊙O与⊙O′是什么位置关系？

⊙O与⊙O′的圆心连线OO′与公共弦AB是什么关系？

图1

学生在纸上用圆规画出两个圆，寻找A、B两点的关系.然后由生甲进行展示：

在图中，⊙O与⊙O′的位置是相交关系；⊙O与⊙O′的圆心连线OO′与公共弦AB是垂直关系.如图2.

师：建立下列概念并展示相关知识体系网络（知识回顾），在学生再次重温知识体系之后思考两个圆相切的性质规律并进行讨论交流.

图2

图3

学生分组讨论并交流“当两个圆相切时，切点一定在圆心的连线上”的证明过程.

师：通过上面的一些关系，你们可以发现两个圆相交或相切时一般能作哪些辅助线？

（学生举手回答）

生乙：两圆相交时常常作的辅助线有：（1）两圆的公共弦，（2）两圆圆心的连线，（3）创设由半径、公共弦的一半组成的直角三角形；两圆相切时常引辅助线有：（1）公共切线，（2）两圆圆心的连线，（3）创设由半径的延长线、公共弦在内的直角三角形等.

3.通过电子白板展示例题

例题：如图4，用半径R=30mm、r=20mm的玻璃球测量一内直径为d的圆柱形笔筒.测得玻璃球顶点与圆柱形笔筒口所在平面的距离分 别为a=20mm，b=60mm，则圆柱形笔筒的内直径d是多少？

图4

设计目的：通过身边的常见文具创设问题情境，有利于激发学生探究的动力.本例题旨在让学生认识两圆相交常常作的第（3）种辅助线，“创设由半径延长线、公共弦在内的直角三角形”.再用体现数形转换数学思想的勾股定理来进行运算推理，从而达成帮助学生数学建模的目的.在课堂上，本例题是在教师的引导后学生自主探究完成的.最后由学生通过投影展示结果：

在图中作辅助线，如图5，创设直角△O1O2A.

则斜边O1O2=R+r=50（mm），直角边O2A=r+b-a-R=30（mm）.

根据勾股定理，另一条直角边O1A=40mm.

故d=40+R+r=90（cm）.

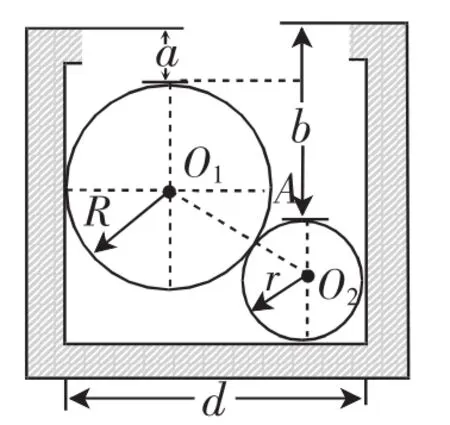
图5

3.通过导学案分组做课堂练习

习题1：（江苏南京）如图6，⊙O1、⊙O2的圆心O1、O2均在直线l上，⊙O1的半径为2cm，⊙O2的半径为3cm，O1O2=8cm.圆O1以1cm/s的速度沿直线l向右运动，7s后停止运动，在此过程中，圆O1与圆O2没有出现的位置关系是（ ）.

A.外切 B.相交 C.内切 D.内含

图6

选题目的：旨在让学生理解两个圆的关系：外切、相交、内切、内含.而这些关系需要学生通过两个圆心的距离进行判断.

习题2：（江苏南通）如图7，三个半圆依次相外切，它们的圆心都在x轴上，并与直线相切.设三个半圆O1、O2和O3的半径依次为r1、r2和r3，则当r1=2时，r3是多少？

选题目的：旨在让学生灵活运用相切圆和圆的相切直线的关系，通过相似三角形或勾股定理解决数学问题.试题涵盖了一次函数的性质、相切圆的性质，让学生通过一次函数的解析式得出直线与x轴的夹角是30°，可以通过作辅助线“三个圆与直线的切点分别与各圆心的连线”，组成三个直角三角形，再进行推理计算.

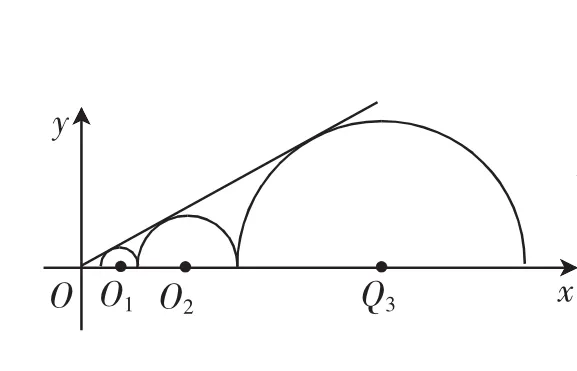
图7

图8

习题3：（江苏泰安）如图8，AB、CD是⊙O的两条互相垂直的直径，点O1、O2、O3、O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）.

A.8 B.4 C.4π+4 D.4π-4

选题目的：通过圆与圆相交的位置关系，和相关扇形面积的计算，培养学生的数形转换思想，培养学生能够根据已知条件推断正方形内空白面积的建模能力.由扇形COB中两空白面积相等，思考阴影部分面积.在建模过程中，要强化辅助线的作法，让学生在解题过程中熟悉如图9所示的方法.

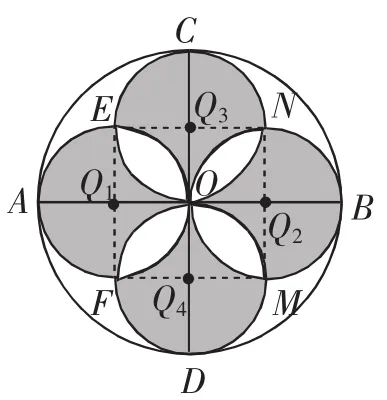
图9

三、课后打磨

本课是圆和圆的位置关系复习课.在教学过程中，教师注重对学生参与数学活动的潜力和自信心的挖掘，培养学生合作交流的意识，以及独立思考的习惯，在针对性较强的中考试题的引领下，让学生瞄准中考考向，是一节符合学生心理发展的示范课.

教师能够及时发现问题、引导学生解决问题，从而进行正向评价，尤其是对学生出现的独特的想法或结论给予鼓励性评价，让学生信心满满，积极参与探究活动.

本节课是建立在激励学生学习兴趣的基础之上的，以促进学生思维发展为目的，更多体现新课程的三维目标.

本课美中不足的是所选试题过于经典，都来自5年前的江苏省试题，而近年来的试题学生基本上已经练习过，建议备课组在近年来江苏省之外的中考试题中选取，这样更能拓宽学生的视野，培养学科素养.F