基于GeoGebra的开放教育“计算方法”可视化教学
2019-06-27汪吉
汪 吉
(武汉市广播电视大学汉阳区分校,湖北 武汉 430050)
引言
“计算方法”是计算数学的分支,是研究用计算机求解数学问题的数值计算方法及其理论的一门课程。[1]本课程具有知识结构分散、算法公式复杂、推导过程繁琐等特点。传统的教学模式多注重讲授算法的基本原理,公式推导和算例演算占据了大部分教学时间,再加上缺乏实验环节的教学,学生普遍感到枯燥乏味,学习兴趣不高,教学效果不理想。
一、“计算方法”教学可视化的意义
随着计算机可视化技术的发展,其在教育教学领域的应用日益广泛。所谓可视化,是指将数据、信息和知识转化为可视的表示形式,从而获得更深层次认识的过程。因此,教学过程的可视化是降低认知难度、增强认知能力,提升教学效果的重要途径。[2,3]
(一)理论教学可视化的意义
众所周知,“计算方法”在教学过程需要大量的数值计算和结果绘图,传统的算式推导和图形绘制浪费有限的教学时间,学生也难以产生数学知识的具体概念,理解起来比较吃力。借助可视化的理论教学,操作有关数学软件,能将算法执行过程中每个步骤的图形和计算结果动态地演示出来,并可不受限制地重复播放。[4,5]这样节省了教学时间,使得教师有更多的精力集中在重难点教学上,更容易把典型的、代表性强的理论和算法讲透,让学生在有限的时间内接受和掌握更多知识。
(二)实验教学可视化的意义
“计算方法”作为与计算机密切结合的数学课程,在进行理论教学的同时配以实验教学,才能使学生真正理解和掌握算法。[6]通过可视化的实验教学,让学生自主操作数学软件,针对不同的数据输入,通过图形直观地反映实验结果的变化,这种交互式体验有利于调动学生的学习积极性,加深学生对所学知识的理解。
二、基于GeoGebra的可视化教学的优势
要实现开放教育“计算方法”教学的可视化,就必须针对开放教育的特点,选择合适的数学软件作为可视化平台。Matlab、Mathematica、Maple等软件虽然数值计算功能强大,但作为商业化软件,对开放教育的学生而言获取有一定难度。其安装过程复杂,运行对计算机硬件配置也有一定要求。想要熟练掌握这些软件进行数学实验,也需要花大量的时间和精力进行学习和训练。
GeoGebra作为开源的数学软件,免费提供适用于计算机、平板电脑、智能手机各种操作系统的版本,能很好地满足开放教育学生“人人皆学、处处能学、时时可学”的开放性学习需求。软件集成了微积分、线性代数、解析几何、概率统计等多种功能模块,特别是图形处理能力强大,能动态呈现代数方程和几何图形的同步变化,非常适于可视化教学,已在欧美许多国家得到大力推广并广受好评。
将GeoGebra引入“计算方法”的教学中,可以很好地解决理论教学效果不佳的问题。教师不仅可以在课堂教学中利用软件的即时演示功能进行讲解,还可以利用其便利的分享功能进行教学。软件的程序文档可导出为GIF动图或分享到GeoGebra官方网站,并在网页上直接运行。教师也可将源程序文档作为附件分享到国家开放大学学习网相应课程的学习论坛上,供学生下载学习。
将GeoGebra引入“计算方法”的教学中,可以很好地解决实验教学开展困难的问题。地方开放大学(广播电视大学)因受师资情况、课时安排、硬件水平等条件的制约,大都没能安排数学实验。对开放教育的学生而言,进行数学实验的宗旨不在于熟练掌握Matlab等高级语言以便进一步从事研究工作,而是通过实验让学生直观地感受算法的基本原理,比较算法的优劣,加深对学科基础知识的理解,提高学习的主动性和积极性。GeoGebra软件具有免费开源、平台多样、命令简单、易于学习的特点,很适合开放教育的数学实验。学生可以选择在常用的学习设备上安装软件,借助教师发布的实验资源,做到时时、处处自主学习。
三、基于GeoGebra的可视化教学实现
非线性方程求根是“计算方法”的重要内容。一般而言,绝大部分非线性方程都不存在求根公式,很难得到根的准确值,只能通过算法逼近来根的近似值,区间二分法和切线法就是其中的两种经典算法。下面以GeoGebra Classic 5中文版为平台,探讨软件在这两种算法可视化教学中的实现。
(一)区间二分法
1.算法原理
设函数f(x)在[a,b]上连续,若f(a)·f(b)<0,则f(x)在(a,b)上至少有一个根x*。
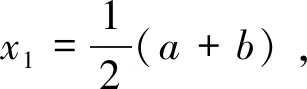
(a)若f(x1)=0,则x*=x1;
(b)若f(a)·f(x1)<0,则x*∈[a,x1]=[a1,b1];
(c)若f(b)·f(x1)<0,则x*∈[x1,b]=[a1,b1].
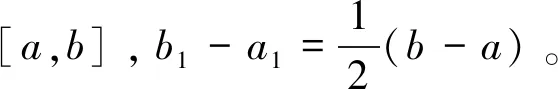
2.算法实现
Step1:在绘图区中新建4个输入框,分别对应方程、区间端点、精度。
Step2:在绘图区中新建按钮button1,命名为“初始化”。右击按钮,选择“属性/脚本”,在“单击时”标签中选择“GeoGebra脚本”,输入以下命名:
a=0; b=0; 赋值(a,aInput); 赋值(b,bInput); y_a=f(a); y_b=f(b);
l_1={}; l_2={}; l_3={}; l_4={}; l_5={}; l_6={};
i=1; x_0=(a+b)/2; y_0=f(x_0);
r=abs(a-b); e1=lg(r); r_s=科学记数法(r);
c="F"; 设置显示条件(c,false); c1=字母转换为统一码[c];
d="T"; 设置显示条件(d,false); d1=字母转换为统一码[d];
赋值(l_1,i,i-1); 赋值(l_2,i,a); 赋值(l_3,i,b); 赋值(l_4,i,x_0); 赋值(l_5,i,er);
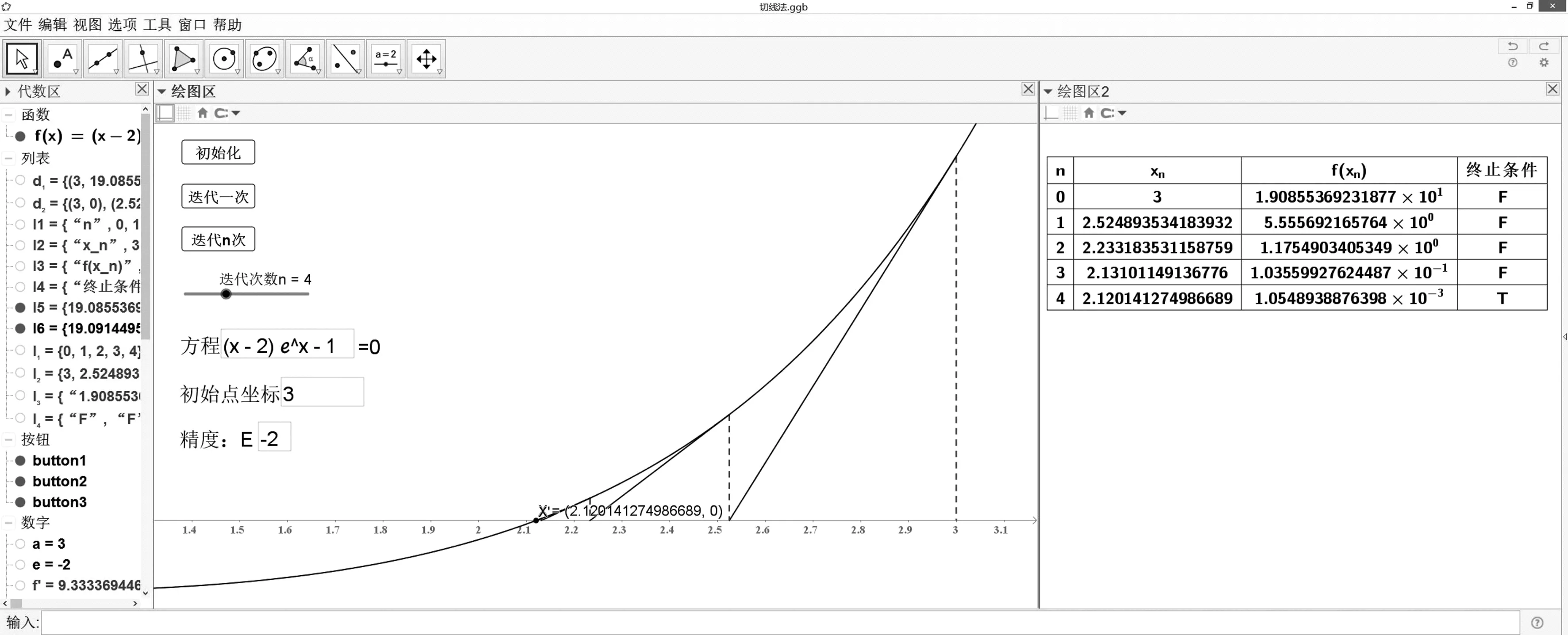
如果((y_0==0)||(e1 设置显示条件(text1,true); Step3:在绘图区中新建按钮button2,命名为“执行一次”。同样在“GeoGebra脚本”中,输入以下命令: 如果(y_a*y_0<0,赋值(b,x_0),赋值(a,x_0)); 赋值(l_1,i+1,i); 赋值(l_2,i+1,a); 赋值(l_3,i+1,b); 赋值(l_4,i+1,x_0); 赋值(l_5,i+1,er); 如果((y_0==0)||(e1 Step4:在绘图区中新建一个滑动条,取值为从1到10的整数,命名为“执行次数n”。新建按钮button3,命名为“执行n次”。在“GeoGebra脚本”中,输入以下命令: 重复(执行次数n,运行单击脚本(button2)); Step5:在指令栏依次输入以下命令: l1=插入("n",l_1,1) l2=插入("a_{n-1}",l_2,1) l3=插入("b_{n-1}",l_3,1) l4=插入("x_n",l_4,1) l5=插入("abs(a_{n-1}-b_{n-1})",l_5,1) l6=插入("终止条件",l_6,1) text1=表格文本({l1,l2,l3,l4,l5,l6},"cv|_") text2="=0" text3="精度:E" text4=文本("(a,b)",(A'+B')/2,false,false) A=(a,0) B=(b,0) X=(x_0,0) A'=A+(0,1) B'=B+(0,1) u=向量(A',B') v=向量(B',A') g=如果(f(a)<0,线段(A',(a,f(a))),如果(f(a)<1,线段(A,A'),线段(A,(a,f(a))))) h=如果(f(b)<0,线段(B',(b,f(b))),如果(f(b)<1,线段(B,B'),线段(B,(b,f(b))))) 3.算法实例 以区间二分法求方程(x-2)ex-1=0的根(精确到10-2)。因为f(2)·f(3)<0,故取初始有根区间为(2,3)。算法的动态演示界面如图1。 图1 区间二分法的动态演示 在输入框中输入方程、区间端点、求解精度等参数后,单击“初始化”按钮,完成参数的输入。单击“执行一次”按钮后算法完成一次计算,执行过程的图形同步显示在绘图区,执行次数、区间端点坐标、区间中点坐标、是否满足终止条件等均以表格形式同步显示在绘图区2中。拖动滑动条“执行次数n”,然后单击“执行n次”按钮,即可得到n次计算后的结果。 随着执行次数的递增,有根区间的范围逐步缩小,区间中点与方程的根逐步接近。执行7次后,终止条件由“F”变为“T”,得到符合精度要求的近似解。 1.算法原理 对于非线性方程f(x)=0,设x0是根x*的一个初始近似值。 若y=f(x)二次连续可导,过f(x)上的点(x0,f(x0))做切线,切线方程为y=f(x0)+f′(x0)(x-x0),则取此切线与x轴交点的横坐标x1作为x*的一个新的近似值。 重复上述过程,得到近似解数列{xn},其迭代公式为: 2.算法实现 Step1:在绘图区中新建3个输入框,分别对应方程、初始点坐标、精度。 Step2:在绘图区中新建按钮button1,命名为“初始化”。右击按钮,选择“属性/脚本”,在“单击时”标签中选择“GeoGebra脚本”,输入以下命名: i=1; x_0=0; 赋值(x_0,a); y_0=f(x_0); r=lg(abs(y_0)); X=(x_0,0); X'=(x_0,y_0); y_s=科学记数法(y_0); 设置显示条件(y_s,false); c=如果(r l_1={}; l_2={}; l_3={}; l_4={}; d_1={}; d_2={}; 赋值(l_1,i,i-1); 赋值(l_2,i,x_0); 赋值(l_3,i,y_s); 赋值(l_4,i,c); 赋值(d_1,i,X'); 赋值(d_2,i,X); Step3:在绘图区中新建按钮button2,命名为“执行一次”。同样在“GeoGebra脚本”中,输入以下命令: x_1=x_0-y_0/df; 设置显示条件(x_1,false); 赋值(i,i+1); 赋值(x_0,x_1); 赋值(l_1,i,i-1); 赋值(l_2,i,x_0); 赋值(l_3,i,科学记数法(y_0)); 赋值(l_4,i,c); 赋值(d_1,i,X'); 赋值(d_2,i,X); Step4:在绘图区中新建一个滑动条,取值为从1到10的整数,命名为“执行次数n”。新建按钮button3,命名为“执行n次”。在“GeoGebra脚本”中,输入以下命令: 重复(执行次数n,运行单击脚本(button2)); Step5:在指令栏依次输入以下命令: l1=插入("n",l_1,1) l2=插入("x_n",l_2,1) l3=插入("f(x_n)",l_3,1) l4=插入("终止条件",l_4,1) l5=序列(线段(元素(d_1,i),元素(d_2,i)),i,1,长度(d_1)) l6=序列(线段(元素(d_1,i),元素(d_2,i+1)),i,1,长度(d_1)) df=元素(映射(g(x_0),g,{导数(f)}),1) text1=表格文本(l1,l2,l3,l4,"cv|_") text2="=0" text3="精度:E" X=(x_0,0) X'=(x_0,y_0) 3.算法实例 以切线法求方程(x-2)ex-1=0的根(精确到10-2),取初始点x0=3。算法的动态演示界面如图2。 图2 切线法的动态演示 切线法的可视化操作方法与区间二分法相同,算法执行过程中每一步的切线、切线与x轴交点等图形同步显示在绘图区,有关数据以表格形式显示在绘图区2中。拖动滑动条“执行次数n”,然后单击“执行n次”按钮,即可得到n次计算后的结果。。随着执行次数的递增,切线与x轴的交点逐步接近方程的根。4次执行后,终止条件由“F”变为“T”,得到符合精度要求的近似解。从算法的对比演示明显看出,切线法的收敛速度比区间二分法快。 在教学实践中,学生可以自主修改方程、初始值等参数,进一步观察参数对结果的影响、比较算法的收敛速度,通过这种交互式的体验加深对算法的理解。 在开放教育“计算方法”课程的教学中引入GeoGebra软件,有助于实现理论教学和实验教学的可视化,提高了教学过程的直观性,使原本枯燥难懂的知识更易掌握,激发了学生的学习兴趣,实现了教与学的良性互动,并潜移默化地培养了学生的数学思想和创新意识,提高了开放教育人才培养的质量。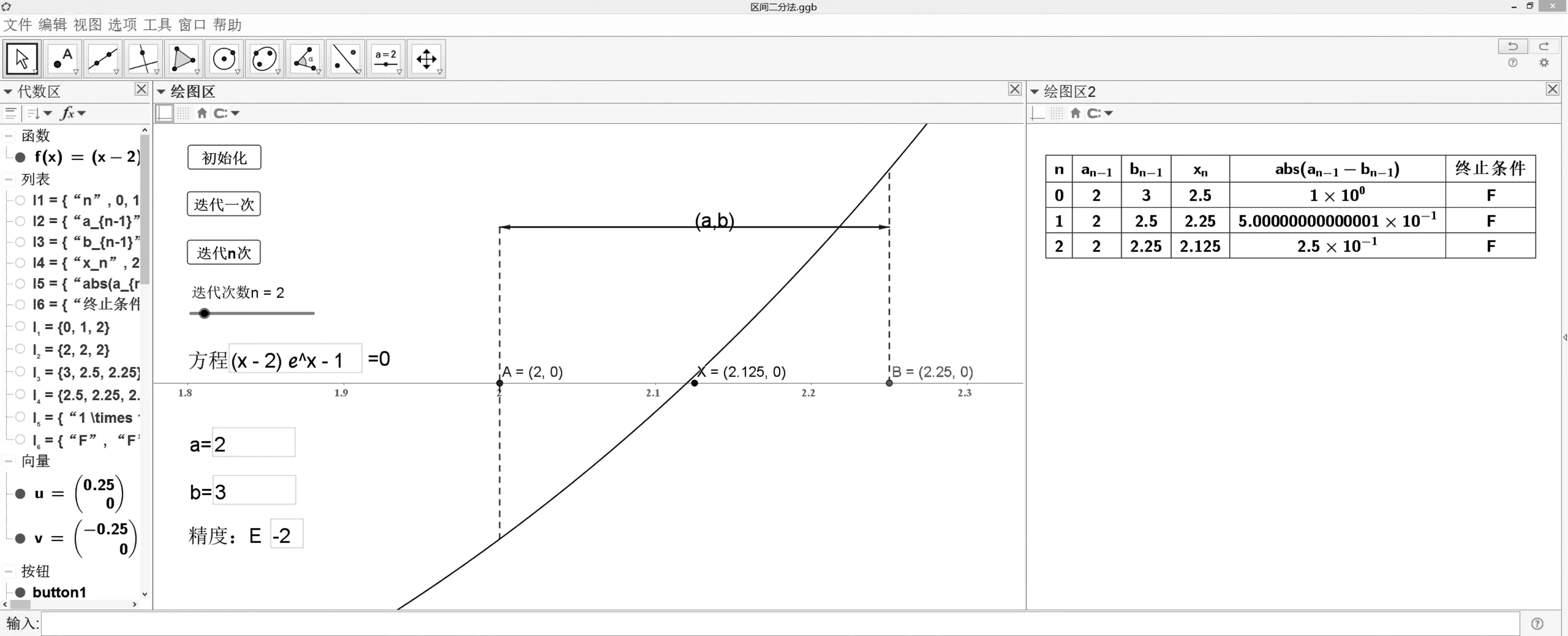
(二)切线法
结语
