胶轮压路机制动安全距离模型及参数敏感性分析*

杨 青， 胡钢华， 徐文毅， 林文岩， 谢 铭， 龚梦琦

(1.浙江师范大学 道路与交通工程研究中心，浙江 金华 321004；2.金华市交通工程质量监督站，浙江 金华 321013；3.浙江正方交通建设有限公司，浙江 金华 321025;4.浙江临金高速公路有限公司，浙江 杭州 310024)

0 引 言

胶轮压路机是路面施工中的常用设备，因其设备质量大、行驶速度快、需场地施工人员配合等作业特征，一旦发生刮擦与碰撞，不但对设施或设备造成损毁，而且会危及施工人员的生命安全，高频作业带来的安全隐患已成为道路行业关注的焦点.未能在安全距离内制动是诱发事故的关键原因[1]，因此及时判断行驶危险状态，实时预测制动的安全距离，并采取制动措施，对于保障胶轮压路机的施工安全具有重要意义.

目前，国内外学者已对智能防撞控制领域展开了广泛研究，现有成果主要集中在汽车安全制动技术方面.袁浩等[2]利用制动加速度来表征制动过程，阐明了汽车不同制动阶段的特征，改进了停车视距计算公式，并建立了制动安全距离模型； Sharizli等[3]基于虚拟样机软件系统，在不同荷载和速度条件下，对汽车制动性能进行了仿真模拟，为制动模型的修正提供了数据支撑；张滨刚等[4]通过大量实车试验，挖掘出影响制动距离的特征参数，结合汽车制动过程中的动态性能分析，补充完善了制动距离的预测模型;康成龙等[5]研究了路面摩阻系数对汽车安全制动距离的影响，并利用仿真平台探讨了路面摩阻系数对模型的影响规律；陈瑶等[6]针对公路环境因素，分析了驾驶员的制动反应时间对汽车制动的影响，构建了不同反应时间的制动计算模型；裴晓飞等[7]利用安全距离模型，开发了汽车防撞系统，并基于目标检测算法，对影响模型参数进行了标定.事实上，构建制动安全距离模型是车辆进行安全制动的重要保障，也必将为未来无人驾驶环境下的车路协同平台开发提供前期理论基础.然而，当前国内外对于路面施工车辆的制动安全距离模型及其参数影响敏感性的研究较少，加之复杂的场地施工环境，导致施工碰撞事故的发生率居高不下[8].如何定量分析影响施工车辆制动安全距离的相关参数并构建有效的制动安全距离模型，是路面施工安全技术领域亟待解决的关键问题.

基于此，笔者针对胶轮压路机，在探讨制动过程阶段特征的基础上，结合胶轮压路机施工场地的实际工作条件，构建了制动安全距离模型，探讨了影响制动安全距离的参数敏感性，利用现场实测数据验证了制动安全距离模型的精确度并进行了模型校正分析.研究成果以期为胶轮压路机制动安全防撞控制系统的开发提供理论支撑，为最大程度地减少胶轮压路机施工碰撞事故的发生提供技术保障.

1 胶轮压路机制动模型及参数取值

1.1 制动安全距离模型

充分考虑胶轮压路机现场制动过程的实际特征，将胶轮压路机制动过程划分为障碍物识别、制动力缓冲、制动力稳定和车辆停止4个阶段，具体包括制动反应、制动力上升、全制动稳定3个时间范围，其中，制动反应时间tf=t1、制动力上升时间ts=t2-t1、全制动稳定时间tw=t3-t2,如图1所示.制动反应阶段是指从驾驶员接受到制动信号至传动装置开始制动的过程；制动力上升阶段是指胶轮压路机开始制动，逐渐产生摩阻力并达到最大值的整个过程；全制动稳定阶段是指胶轮压路机保持最大制动力，直到车辆停止的整个过程.

基于车辆制动过程的运动学和能量守恒定律，综合考虑制动反应时间、路面摩阻系数及施工车速等参数，通过推导得到胶轮压路机的制动安全距离模型为

(1)

图1 胶轮压路机制动过程阶段特征

式(1)中：S为胶轮压路机的制动安全距离；S1,S2,S3分别为制动反应阶段、制动力上升阶段和全制动稳定阶段内胶轮压路机的行驶距离；v0为胶轮压路机开始制动时的初始速度,即胶轮压路机的施工车速；a为全制动稳定阶段的加速度，a=μg，μ为路面摩阻系数，g为重力加速度.

1.2 模型参数取值

胶轮压路机制动安全距离模型除受初始速度的影响外，路面摩阻系数和制动反应时间对其影响也不容忽视.路面摩阻系数由胶轮压路机的碾压轮滑移率、车速、轮胎荷载、沥青路面状态等指标共同决定[9].胶轮压路机采取制动措施后，碾压轮的制动过程一般包括碾压轮滚动和碾压轮未滚动2个阶段.碾压轮滑移率从0增大到临界滑移率λp时，纵向摩阻系数也逐渐增大，达到峰值μmax，此阶段碾压轮处于滚动状态；随着制动过程的发展和滑移率的增大，摩阻系数逐渐减小至稳定值，该阶段碾压轮处于未滚动状态.黄如波等[10]经过大量实车试验，得到胶轮压路机与施工路面之间的路面摩阻系数的取值为0.4～0.7.

制动反应时间受驾驶员反应时间和胶轮压路机制动装置反应灵敏度的双重影响[11].其中，驾驶员作为道路施工的参与者，由于年龄、性别及生理心理状态的差异，使得驾驶员识别和判断危险信息所需的反应时间不同.李霖等[12]调取大量驾驶员行驶样本，分析了真实交通危险工况下的制动反应时间，得到驾驶员的制动反应时间为0.4～2.0 s.胶轮压路机制动装置的反应灵敏度决定了机械传动反应时长，受车辆特征、累计施工总时间、机械零件磨损程度、施工工况等因素的综合影响.尹继瑶[13]通过研究压路机的输出特性与传动效率，将机械装置传动方式分为液压式和气压式2类，分别对应机械的制动反应时间为0.2～0.4 s和0.4～0.8 s.综上所述，结合路面摩阻系数和胶轮压路机制动装置反应灵敏度，并考虑场地的实际工作条件，制动反应时间为2.5 s时即为危险工况.

2 制动安全距离的参数敏感性分析

2.1 参数敏感性评价

为了探讨初始速度、路面摩阻系数、制动反应时间等参数的变化及参数间相互耦合作用机制，采用Sobol全局敏感性分析方法，将影响制动安全距离模型的函数关系表达为单一控制参数和组合控制参数的形式[14]，如式(2)所示.

(2)

式(2)中：f(X1,X2,X3)为模型构成的函数关系；X1为初始速度v0；X2为路面摩阻系数μ；X3为制动反应时间tf.

制动安全距离的参数敏感性分析在危险工况条件下开展，即制动反应时间取2.5 s，以初始速度和路面摩阻系数为输入，制动安全距离为输出，定量计算2个参数对输出结果的影响，并分析各参数的影响规律.参数的输入、输出情况如表1所示.

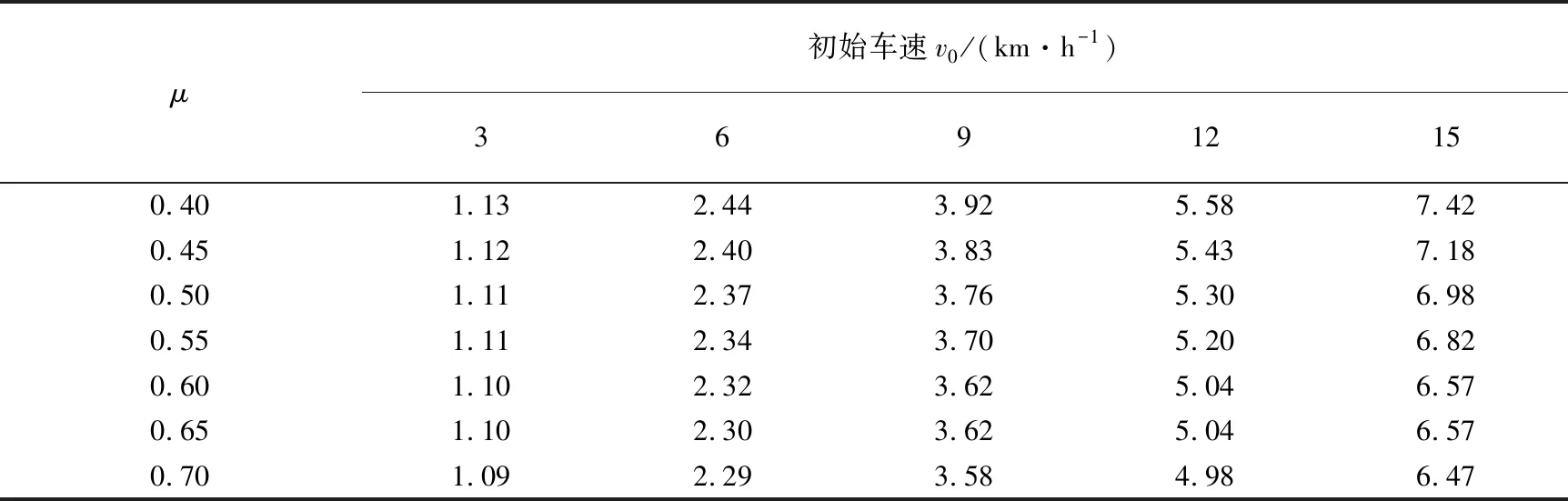
表1 不同v0,μ条件下的制动安全距离 m

当各参数正交时，该模型具有唯一的分解形式.模型总方差可以由单个参数作用方差及各参数之间相互作用的方差组成，如式(3)所示.

D=D(v0)+D(μ)+D(v0, μ).

(3)

式(3)中：D为模型总方差；D(v0)为初始速度单独作用的方差，计算得D(v0)=5.22；D(μ)为路面摩阻系数单独作用的方差，计算得D(μ)=0.04；D(v0, μ)为初始速度和路面摩阻系数共同作用的方差，计算得D(v0, μ)=2.64.

对式(3)进行归一化迭代处理[15]，通过计算得到模型的敏感度关系为

S(v0)+S(μ)+S(v0, μ)=1.

(4)

式(4)中：S(v0)为初始速度一阶敏感度；S(μ)为路面摩阻系数一阶敏感度；S(v0, μ)为二阶敏感度.初始速度的总敏感度为S(v0)和S(v0, μ)之和，计算得到它的值为0.141 6；路面摩阻系数的总敏感度为S(μ)和S(v0, μ)之和，计算得到它的值为-0.017 0.由总敏感度的分析结果可知：1)在场地实际工况相同的情况下，初始速度对制动安全距离的影响远远大于路面摩阻系数；2)初始速度与制动安全距离呈正相关，当胶轮压路机施工车速增大时，制动安全距离增大；3)路

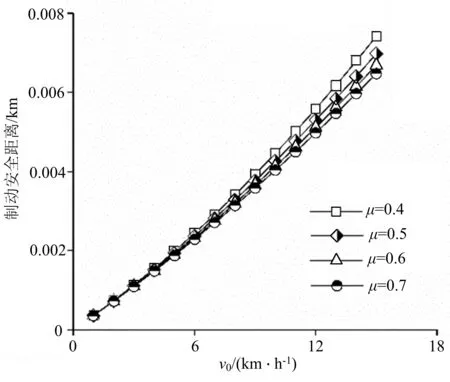
图2 初始速度对制动安全距离的影响

面摩阻系数与制动安全距离呈负相关，路面摩阻系数越大，制动安全距离越小.

2.2 模型参数对制动安全距离的影响分析

为进一步定量分析模型参数对制动安全距离的影响规律，探讨了不同路面摩阻系数条件下初始速度对制动安全距离的影响规律和不同初始速度条件下路面摩阻系数对制动安全距离的影响规律，分析结果如图2和图3所示.由此可知：1)初始速度对制动安全距离的影响呈现一致性，随着初始速度的增大，制动安全距离显著提升；2)当初始速度小于6 km/h时，路面摩阻系数对制动安全距离的影响可忽略不计，当初始速度大于10 km/h时，制动安全距离增幅明显；3)路面摩阻系数对制动安全距离的影响受初始速度的影响显著，初始速度越大，影响程度越显著；4)当初始速度小于6 km/h时，影响曲线基本保持水平，路面摩阻系数影响程度可忽略不计，当初始速度大于12 km/h时，路面摩阻系数会对制动安全距离产生较大的影响.

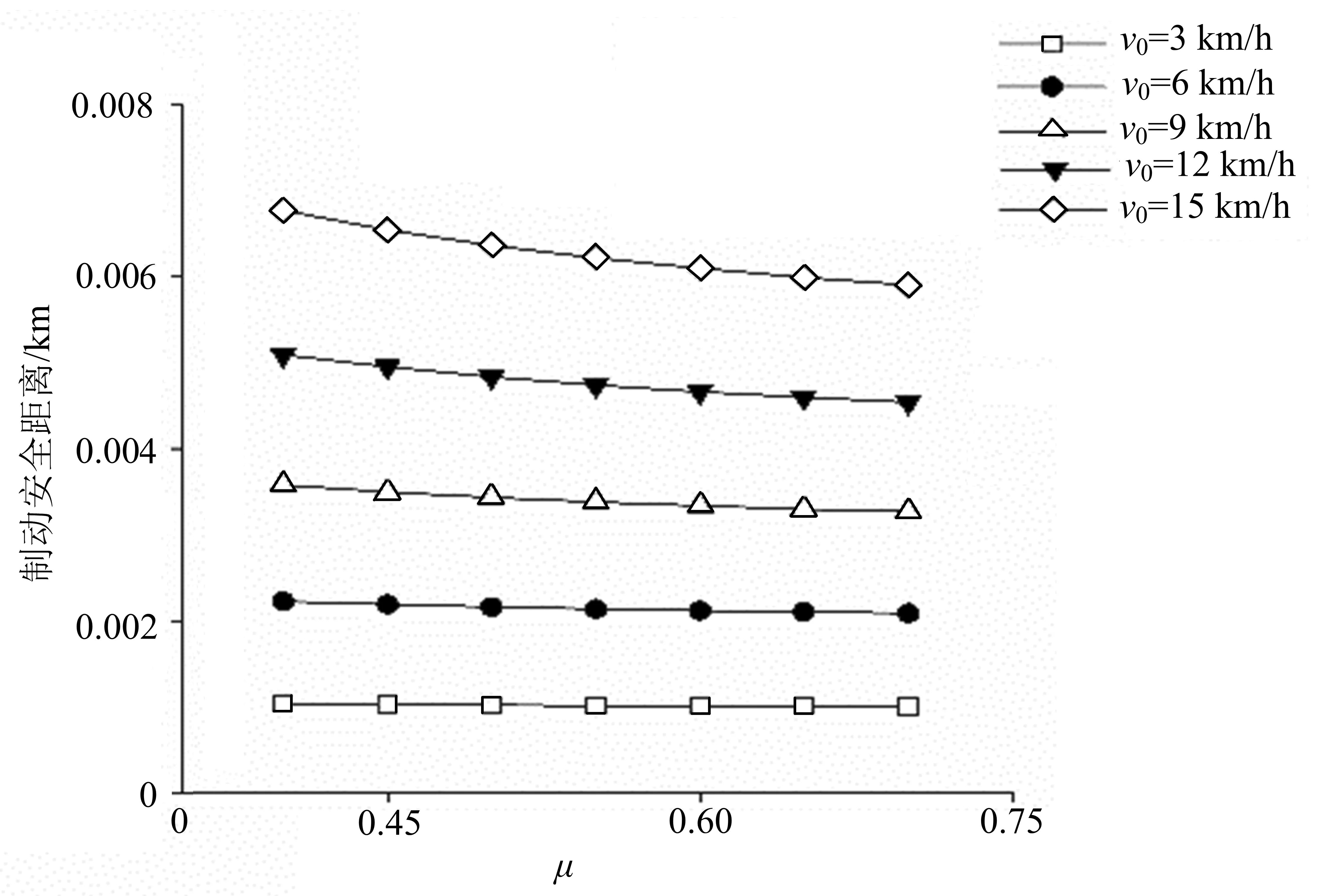
图3 路面摩阻系数对制动安全距离的影响

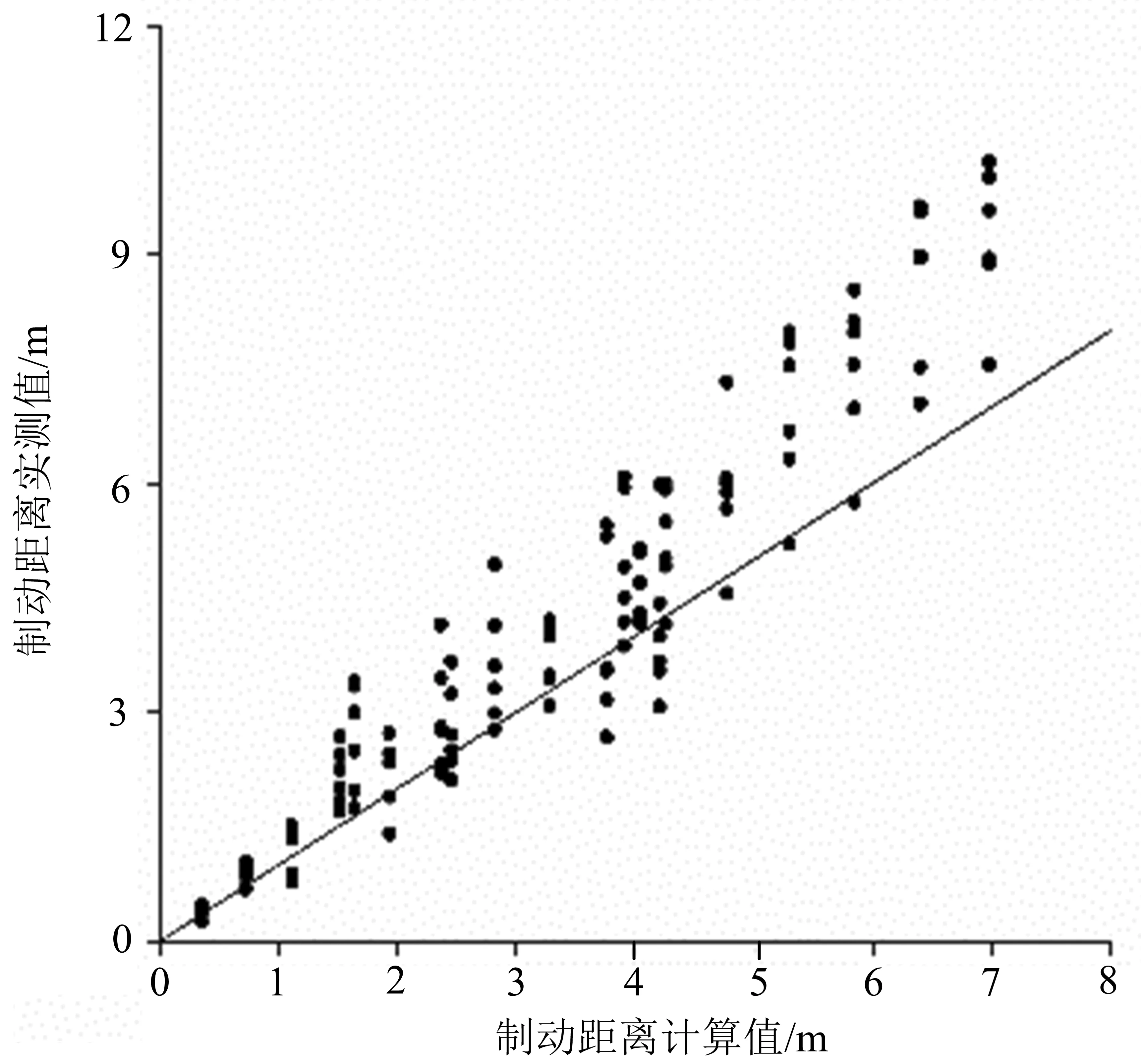
图4 制动距离的实测值与计算值

3 制动安全距离模型验证

3.1 制动距离测定

选取XG6301P型胶轮压路机为研究对象，进行场地实际工作条件下的制动距离测试，行驶速度(即制动时的初始速度)控制在0～8 km/h，路面摩阻系数由摆式摩阻仪测量获取.制动距离实测值与计算值的误差分析结果如图4和图5所示.由此可知：制动安全距离计算值的误差变化为0.23～3.23 m，其中0～2 m的误差占比为85.84%，且对应的行驶速度主要集中在0～6 km/h，表明该模型对低车速条件下的制动距离具有良好的表征能力.

3.2 模型修正

为增强胶轮压路机制动安全距离模型对较高施工速度的适应能力，引入修正系数(λ)对制动安全距离进行校核，如式(5)所示.通过测试数据的线性拟合，得到λ与v0的对应关系,如式(6)所示.修正后制动安全距离的计算值与实测值误差分析结果如图6和图7所示.由此可知：修正后计算值误差仅存在于0～2 m处，占比为100%，且误差主要集中在0～1 m处，相较修正前提高了8.33%，表明修正后的制动安全距离模型对于施工速度的适应能力更强，模型预测精度更加准确.

S实测=λS计算；

(5)

λ(v0)=1.203+0.001×v0.

(6)

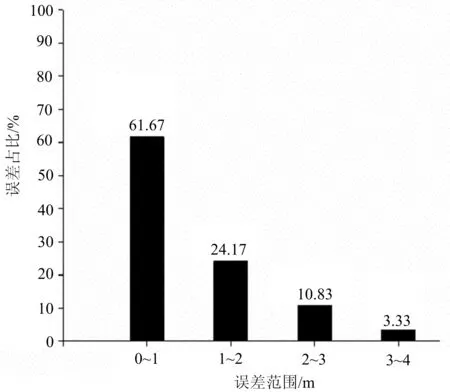
图5 计算值误差的分布直方图

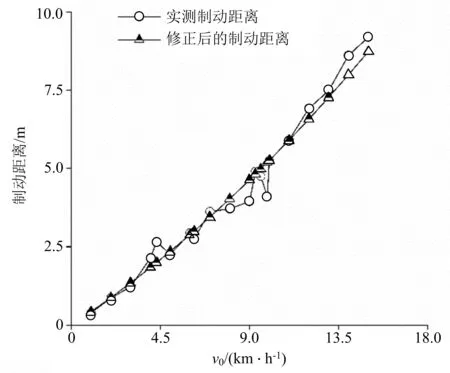
图6 实测值与模型修正值的对比

4 结 论

在建立胶轮压路机制动安全距离模型、分析模型参数取值范围的基础上，利用全局敏感性分析方法评价了影响制动安全距离的参数特征，并定量揭示了模型参数对制动安全距离的影响规律.主要研究结论如下：

1)胶轮压路机制动安全距离模型充分考虑了制动反应、制动力上升、全制动稳定的阶段特征，综合了初始速度、路面摩阻系数及制动反应时间等参数的影响，模型构建过程与胶轮压路机的实际工况条件相符，应用前景良好.

2)初始速度、路面摩阻系数和制动反应时间共同决定着胶轮压路机的制动安全距离，建议应从现场的实际工况出发，结合模型参数的影响规律，综合确定胶轮压路机的制动安全距离.

3)初始速度、驾驶员反应时间及车辆制动反应时间对胶轮压路机制动安全距离的影响更为显著，实际施工过程中,选择机械传动良好的胶轮压路机、限制施工最高车速、提升驾驶员连续施工专注度等措施，是确保胶轮压路机安全制动的有效方法.

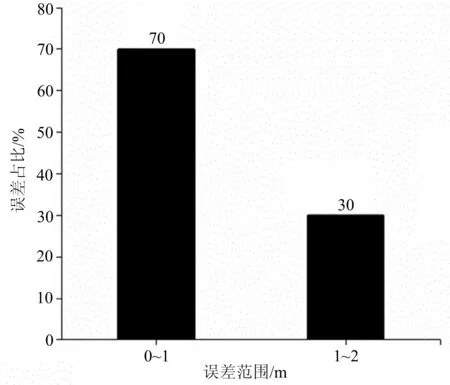
图7 修正后计算值误差的分析直方图