带有随机丢包的扩展卡尔曼滤波稳定性分析*

李闻白, 林飞龙, 潘竹生

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

卡尔曼滤波(Kalman filter,KF)及其扩展形式(extended Kalman filter,EKF)已广泛应用于系统控制[1-2]、信号处理[3-4]、目标跟踪[5]等工程领域.进入21世纪，随着低成本传感、快速计算和无线通信技术的发展，无线网络化控制技术应运而生，并迅速成为研究热点[6].在网络化控制系统中，执行器、传感器、中央控制器和过程监测终端通过无线网络连接，系统的不同组成单元通过无线网络相互交换和传递信息，控制器与过程终端可以实现远程控制与监控.与传统的控制方式相比，无线网络化控制系统具有空间约束少、布设灵活、运行维护成本低等诸多优势，并被公认为是现代控制中最有前途的产业化方向之一[7].在此背景下，针对无线网络化控制系统，通过获取系统的输入、输出观测数据，对系统状态进行最优估计的卡尔曼滤波问题，受到了学术界和工程领域的普遍关注[8-9].

在网络化控制系统中，各个组成单元之间的信息传输、交互依赖于无线网络，数据通过网络传输时将会产生恒定或随机的通信时延，而时延会使控制系统的性能恶化.网络化控制系统中存在的另一个问题是数据丢包.因为通信网络是一种非可靠的传输通道，当受到外界干扰或发生网络拥塞时，网络上的数据在传输时不但存在传输延迟，还可能出现数据包丢失，从而严重影响控制系统的性能，甚至使系统变得不稳定.因此，相比于传统的滤波方法，网络环境下的卡尔曼滤波器分析与设计变得更为复杂，深入研究通信时延、数据丢包对滤波器性能的影响，成为网络化控制领域的重要课题[6-9].

对于网络化控制系统中卡尔曼滤波器的性能问题，Sinopoli等[10]研究了数据丢包对线性卡尔曼滤波状态估计的影响，指出当数据丢包率大于某一阈值时，系统的滤波方差将随时间趋于发散；Liu等[11]分析了存在多组观测值独立丢包的线性卡尔曼滤波模型，并给出了与状态估计稳定性相关的滤波观测值的接收率阈值；文献[12-13]针对网络丢包情形下，基于概率模型分析了线性卡尔曼滤波的状态估计性能，建立了滤波方差小于某个给定常值矩阵的概率上下界；Huang等[14]将通信网络的丢包特性描述为二状态的马尔可夫链，给出了确保线性卡尔曼滤波器稳定的数据恢复率下界；Kluge等[15]面向非线性系统的扩展卡尔曼滤波方法，研究了存在数据丢包情形下系统状态估计的误差特性，并给出了一些确保滤波器满足均方指数稳定性的充分条件.

总的来说，以上研究工作对网络化控制系统中卡尔曼滤波器的性能问题进行了有益的理论和实践探索，但仍有一些问题值得考虑.例如，文献[10-14]中讨论的均是线性卡尔曼滤波模型的状态估计性能，并未涉及在工程实际中应用更加广泛的非线性扩展卡尔曼滤波模型；文献[15]虽然给出了扩展卡尔曼滤波器方差的均方指数稳定性条件，然而其要求系统的量测矩阵可逆，并且与系统矩阵具有相同的维数.这些条件显然过于苛刻，且不符合实际中的大多数扩展卡尔曼滤波模型.本文针对这些问题，进一步发展了文献[14]中的方法和技术手段，通过建立随机系统的峰值方差稳定性指标，深入分析了网络数据丢包对非线性扩展卡尔曼滤波器性能的影响，并在不依赖文献[15]中对系统参数的假设条件下，给出了扩展卡尔曼滤波器满足峰值方差稳定性的充分条件.

1 带有随机丢包的扩展卡尔曼滤波模型

考虑如下的非线性时变系统：

xt+1=f(xt,ut)+Gtwt,t≥0.

(1)

式(1)中：t∈Ν是离散时间；xt∈Rn是系统的状态向量；ut∈Rd是系统的输入向量；在初始时刻t=0时，系统的状态初值为x0.系统的量测方程为

(2)

由于在无线网络环境下，系统量测数据的传输可能存在数据丢包，因此量测方程(2)具有下列形式(t≥1)：

(3)

为此，可引入随机变量γt∈{0,1}来描述t时刻量测数据包的到达或丢失.若γt=1，则表示t时刻的量测数据被成功接收；反之，若γt=0，则表示t时刻的量测数据未被成功接收，即传输信道发生了数据丢包.通常情况下，γt的取值0和1分别被称为信道的失败状态和正常状态.为进一步描述网络传输信道的变化情况，设随机序列γt服从二状态的马尔可夫链，其状态转移矩阵为

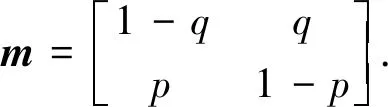
(4)

式(4)中，p>0，q>0分别称为数据传输的失败率和恢复率.例如，1-p表示从正常状态1开始，经过一步转移后信道的传输状态仍为正常状态1的概率.通常称服从上述变化规律的通信信道为Gilbert-Elliott信道模型[14]，若p的取值越小(接近于0)及q的取值越大(接近于1)，则表示网络信道具有更高的传输可靠性.

在此基础上，利用系统的量测方程(3)和信道传输特征γt，并适当修改传统的扩展卡尔曼滤波状态更新方程的推演步骤，可以得到当量测数据传输服从Gilbert-Elliott信道模型时，其扩展卡尔曼滤波的状态预测和量测更新方程分别为：

(5)

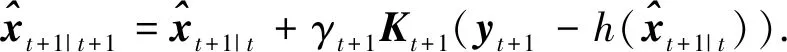
(6)

式(5)和式(6)中:Kt+1是卡尔曼滤波增益；下标t+1|t表示t时刻的状态预测，t+1|t+1表示t+1时刻的状态更新.此外，由于f,h具有一阶连续偏导数，所以可得其雅可比矩阵为

(7)

进一步采用与文献[10]类似的推导方法，可得到扩展卡尔曼滤波的均方误差及滤波增益公式为：

(8)

Pt+1|t+1=Pt+1|t-γt+1Kt+1Ct+1Pt+1|t;

(9)

(10)

其中，方程(8)和方程(10)中的噪声项为

(11)

给出上述带有随机丢包的扩展卡尔曼滤波公式后，下文将重点研究系统状态估计误差的均方误差序列{Pt+1|t}t≥0的演化情况，通过建立系统的峰值方差稳定性，进而导出滤波系统满足该稳定性的充分条件.

2 滤波方差的演化规律

本节的主要目标是给出具有随机丢包的网络信道下，扩展卡尔曼滤波的均方误差的方差的演化规律，并以此建立滤波系统的峰值方差稳定性.为了确保文中的非线性滤波系统是有意义的，对其中部分参数作如下假设：

(H1)状态转移矩阵(4)中的数据传输失败率和恢复率p,q∈(0,1).

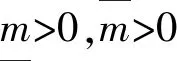
(12)

式(12)中,Mt+k,t为可观测性格拉姆矩阵,即

(13)

并且Φt,t=I，Φi,t=Ai-1Ai…At.

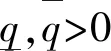
(14)

此外，不失一般性，选取二状态马尔可夫链γt的初值γ0=1.因此，结合非线性系统式(1)、式(3)及γt的取值，系统的滤波方差可以表示为

(15)

式(15)表明，滤波方差序列Pt+1|t在二状态马尔可夫链γt的驱动下，按照γt=0或γt=1两种状态随机地进行跳跃性演化.

下面针对马尔可夫链γt的初始状态γ0=1，递推地引入2组停时(stopping time)序列{τi}i≥1和{βi}i≥1，用来描述γt的跳跃时间：

(16)

由γt的定义可知

(17)

以及下列顺序关系成立:

1<τ1<β1<…<τi<βi<τi+1<….

(18)

引理1在假设(H1)下，停时序列{τi}i≥1和{βi}i≥1中每个元素的取值均为有限值.

证明 由p,q∈(0,1)可知，马尔可夫链{γt}t≥1是遍历的，且具有强马尔可夫性[18].因此，容易验证Pr(τ1=∞)=0，即τ1<∞.注意到γt的强马尔可夫性，则{γτ1+t}t≥1仍为马尔可夫过程，从而Pr(β1=∞|τ1<∞)=Pr(γτ1+t=0,t≥1|τ1<∞)=0.由于τ1<∞，故β1<∞.最后，利用数学归纳法可知，对于每个i≥1都有τi<βi<∞.引理1证毕.

引理2在假设(H1)下，关于驻留时间序列有以下性质：

证明 参见文献[14,18].

具备上述结论后，定义

(19)

下面给出本文的核心概念，即非线性随机系统的峰值方差稳定性.

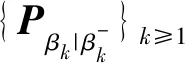
(20)

则称系统具有峰值方差稳定性.式(20)中：‖·‖表示矩阵的谱范数[19]；E{·}为随机变量的数学期望.

3 峰值方差稳定性的充分条件

本文的主要结论以定理1的形式给出，从而获得带有随机丢包的非线性扩展卡尔曼滤波系统具有峰值方差稳定性的充分条件.

定理1考虑网络信道下带有随机丢包的扩展卡尔曼滤波系统，其状态方程和量测方程分别由式(1)和式(3)确定.若系统参数满足下列条件：

(21)

(C2)网络信道的恢复率q有下界qc，并满足

q>qc

(22)

证明 利用系统滤波方差演化的黎卡提方程(15)，定义映射

(23)

式(23)中：F0(Pk|k-1)=Pk|k-1；γk+i=1；i=1,2,…,n-1.由假设条件(H2),(H3)和文献[16-17]中类似的推演方法可知，存在正常数L>0，使得对每个n≥0有

Fn(Pk|k-1)≤LI.

(24)

下面证明满足定理条件(C1)和(C2)的滤波系统具有峰值方差稳定性.

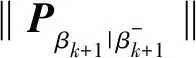
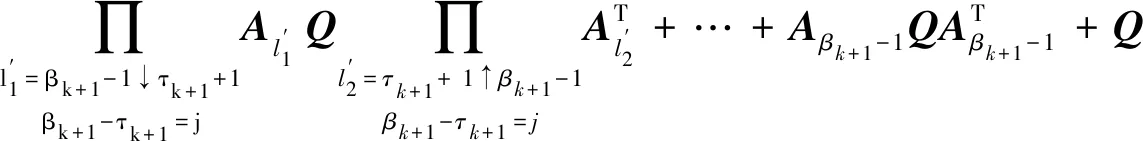
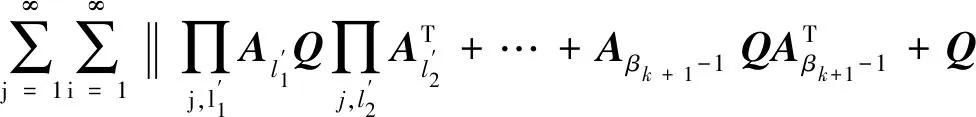
(1-p)i-1p(1-q)j-1qΓ1+Γ2.

(25)

式(25)中：χ{τk+1-βk=i,βk+1-τk+1=j}是示性函数，表达式为

(26)

联立定理1的条件(C1)、(C2)，并结合式(14)和式(24)可得

(27)

(28)

式(27)和式(28)中，L1>0，L2>0是与k无关的常数.因此，

(29)

式(29)进一步表明:对每个k≥0，有

(30)

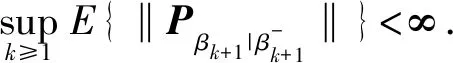
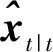
4 结 语

本文基于Gilbert-Elliott网络信道模型，研究了带有随机丢包的扩展卡尔曼滤波器的状态估计性能.通过分析滤波方差序列演化的黎卡提方程，建立了非线性随机系统的峰值方差稳定性，并给出了确保滤波系统稳定的充分条件，具有较好的实用性.在后续工作中，拟面向更一般的网络信道，考虑同时具有通信时延、量化失真及多丢包网络环境下的最优状态估计问题.