在平面直角坐标系中变出“精彩”
2019-06-26龚群友
龚群友
【原题呈现】苏科版九(下)第91页14题:如图1,在平面直角坐标系中,点A的坐标为(2,3),点B的坐标为(3,0)。
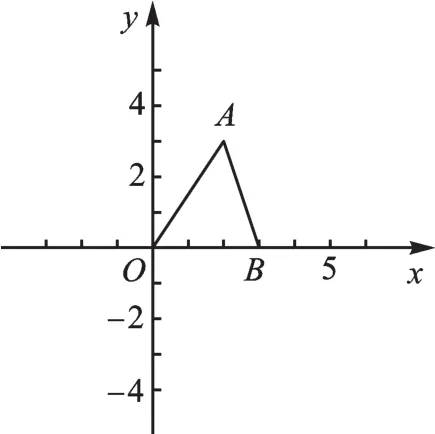
图1
(1)把△AOB沿x轴向左平移1个单位长度得到△A1O1B1,写出点A1、O1、B1的坐标。
(2)把△AOB绕原点旋转180°得到△A2OB2,写出点A2、B2的坐标。
(3)把△AOB沿x轴翻折得到△A3OB,写出点A3的坐标。
(4)以点O为位似中心,在第一象限内把△AOB按相似比2∶1放大,得到△A4OB4,写出点 A4、B4的坐标。
【解析】(1)A1(1,3),O1(-1,0),B1(2,0)。(2)A2(-2,-3),B2(-3,0)。(3)A3(2,-3)。(4)A4(4,6),B4(6,0)。
【点评】(1)图形的平移变换比较简单,整个图形向右(左)平移了a(a>0)个单位,图形的大小、形状不变,则图形上每个点的横坐标加上(减去)a,纵坐标不变;整个图形向上(下)平移了b(b>0)个单位,图形的大小、形状不变,则图形上每个点的纵坐标加上(减去)b,横坐标不变。
(2)图形的旋转变换与平移相比难度略有增加。中心对称变换,需将每个点和旋转中心连接起来,并延长一倍,就得到旋转180°的对应点。以原点为对称中心的中心对称,旋转前后,每一对对应点的横坐标互为相反数,纵坐标也互为相反数。
(3)图形沿x轴翻折,图形的大小、形状不变,图形上每个点的横坐标不变,纵坐标取相反数。
(4)以点O为位似中心,将线段OA、OB延长一倍,对应点的横坐标和纵坐标都乘2。
【拓展1】在平面直角坐标系中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,-1),则点B′的坐标为_______。
【解析】通过画图,不难发现,点A向右平移4个单位长度可得到点A′,则点B同样也是向右平移4个单位长度到点B′,所以B′的坐标为(5,2)。
【拓展2】△ABC在方格纸中的位置如图2所示。
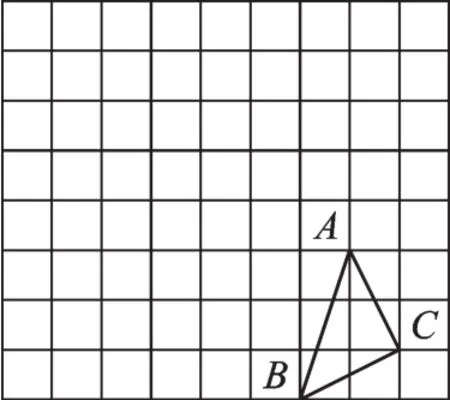
图2
(1)请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为(2,-1),(1,-4),并求出C点的坐标。
(2)作出△ABC关于x轴对称的△A1B1C1,再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2,并写出C1、C2两点的坐标。
(3)观察△A1B1C1和△A2B2C2,其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出是什么变换。
【解析】(1)如图3建立平面直角坐标系,点C的坐标为(3,-3)。(2)如图3,点C1的坐标为(3,3),点C2的坐标为(-3,3)。(3)能,是轴对称变换。
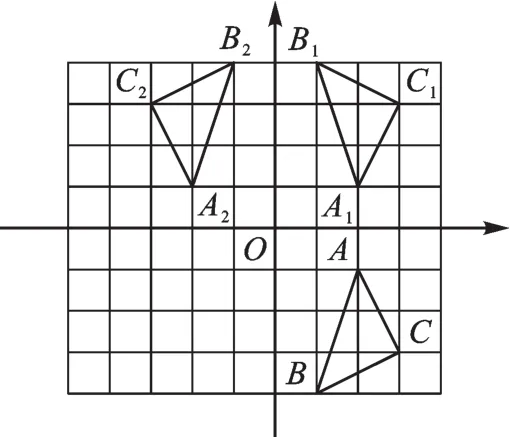
图3
【拓展3】如图4,若点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3)。
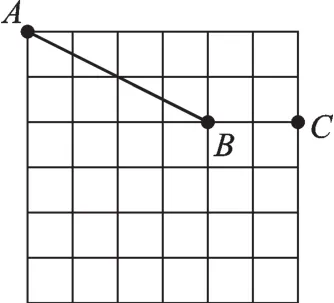
图4
(1)建立恰当的平面直角坐标系,并画出点D(3,-1),连接CD。
(2)小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_______。
【解析】(1)如图5所示。(2)根据旋转的基本性质可以得到,对应点到旋转中心的距离相等,因此旋转中心应为两对对应点连线的垂直平分线的交点。若点A与点C为对应点,点B与点D为对应点,则旋转中心的坐标为(1,1);若点A与点D为对应点,点B与点C为对应点,则旋转中心为(4,4)。所以本题的答案为(1,1)或(4,4)。
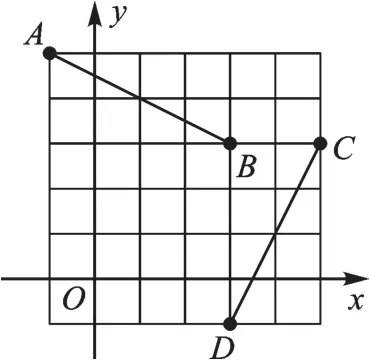
图5
【拓展4】在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕原点O按逆时针方向旋转30°得到点P1,延长OP1到点P2,使OP2=2OP1;再将点P2绕原点O按逆时针方向旋转30°得到点 P3,延长 OP3到点 P4,使 OP4=2OP3……如此继续下去。求:(1)点P2的坐标;(2)点P2019的坐标。
【解析】同学们可根据题意画图分析。
(1)作P2M⊥x轴于M。
∵OP2=2OP1=2OP0=2×1=2,∠P2OM=30°,
∴MP2=2·sin30°=1,OM=2·cos30°=
∴点P2的坐标为()。
(2)按照题中的变化规律,点P5、P6落在y轴的正半轴上,点P23、P24又回到x轴正半轴上。
∵2019÷24=84……3,
∴点P2019落在第一象限内,且OP2019与x轴的夹角为60°。
又∵OP3=OP2=2,OP5=OP4=22,OP7=OP6=23……
∴OP2019=OP2018=21009。
∴点P2019的坐标为(21008,)
以上四个拓展由简单到复杂,由特殊到一般。同学们在解决这类问题的时候,一定要“笔下有图”,结合图形变化,在平面直角坐标系中画出对应图形,即可顺利解决问题。
